Rotation Questions and Answers
Physics
RotationThis section contains 35 SINGLE CORRECT TYPE questions Each question has 4 Read More The following bodies have same mass and radius The body with less moment of inertia about geometric axis is O Solid sphere Phy Section A O Hollow sphere O Disc

Physics
RotationA thin circular ring of mass M and radius R is rotating in a horizontal plane about an axis vertical to its plane with a constant angular velocity o If two objects each of mass m be attached gently to the opposite ends of a diameter of the ring the ring will then rotate with an angular velocity AIPMT 2010 1 3 M M m M M 2m 2 4 M 2m M 2m M 2m M

Physics
Rotationout slippi A cylinder of mass m and radius R is rolling horizontal surface with angular velocity oo The velocity of centre of mass of cylinder is woR The cylinder comes across a step of height R 4 Assume required friction is present at edge of the step Answer the following questione hased on abou 13 A Find the minimum angular velocity wo of cylinder so that cylinder rides up the step without slipping or jumping 2 3g 5 VR 5 3g 2VR C B D 3 3g 5VR o R g 3R R 4
Physics
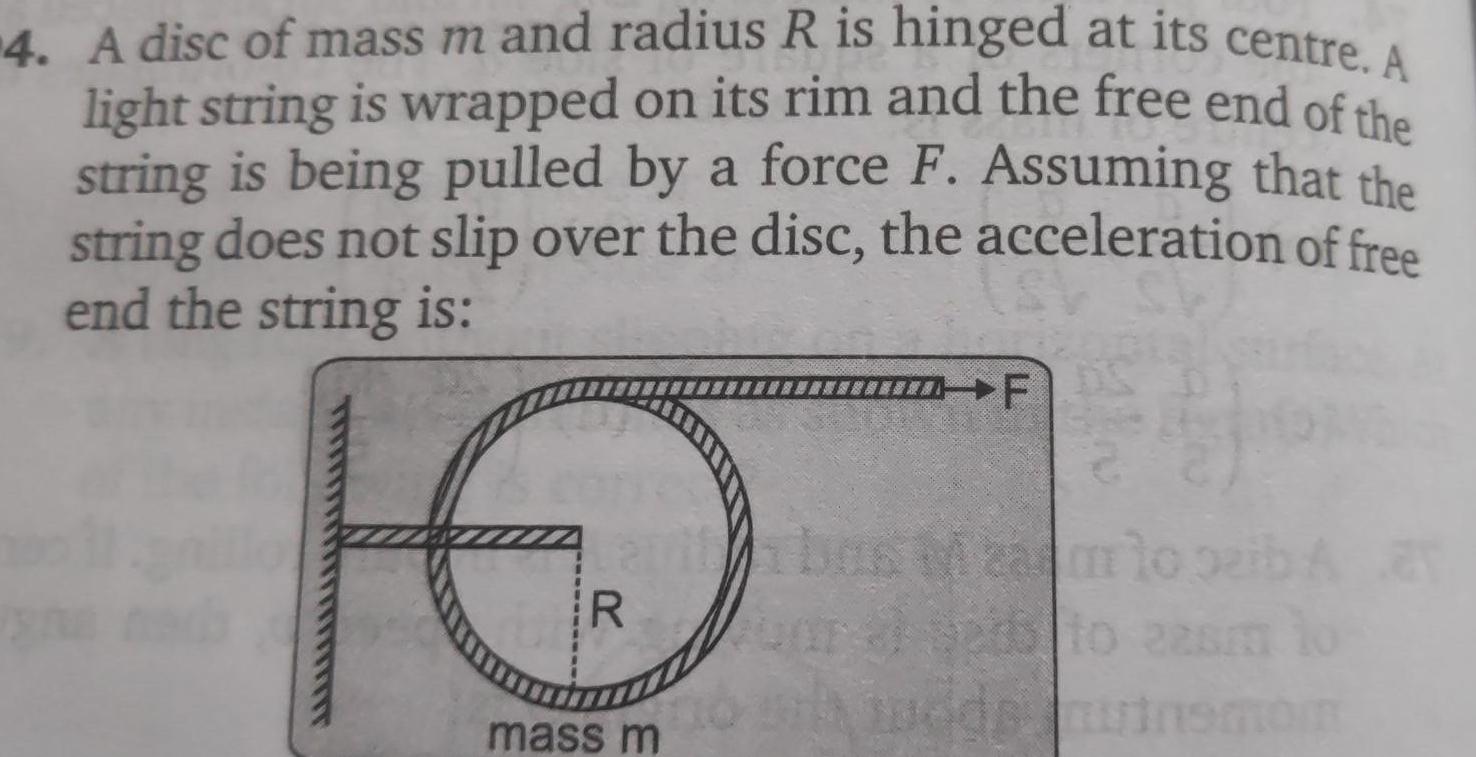
Rotation4 A disc of mass m and radius R is hinged at its centre A light string is wrapped on its rim and the free end of the string is being pulled by a force F Assuming that the string does not slip over the disc the acceleration of free end the string is R mass m F pode muinsmon
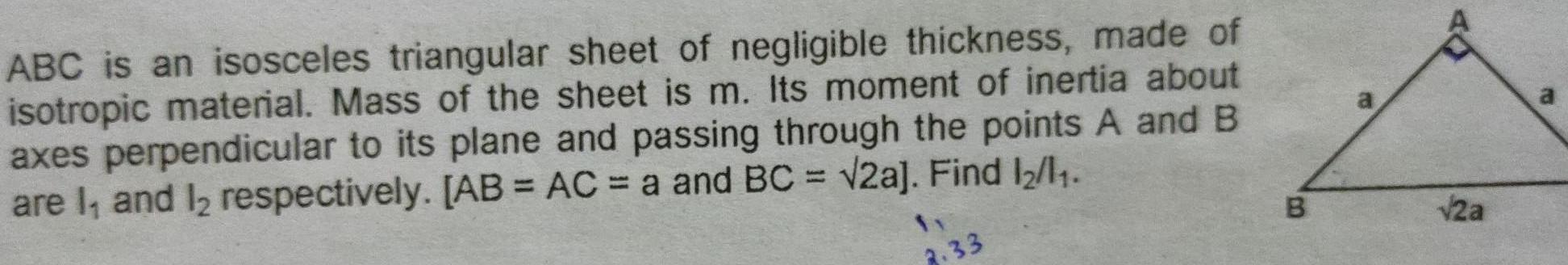
Physics
RotationABC is an isosceles triangular sheet of negligible thickness made of isotropic material Mass of the sheet is m Its moment of inertia about axes perpendicular to its plane and passing through the points A and B are 1 and 1 respectively AB AC a and BC 2a Find 12 11 2 33 B 2a ro

Physics
Rotation51 A thin rod AB of length is kept vertical on a horizontal floor such that end A is in contact with floor If the rod is allowed to fall without slipping at end A then its angular velocity just before hitting the ground is 1 3gl 3 lal 2 2 gl 4 2g

Physics
RotationQuiz Quiz If earth were to stop spinning then your weight on equator will be A B C D heavier by around 0 5 heavier by around 5 less by around 0 5 less by around 5
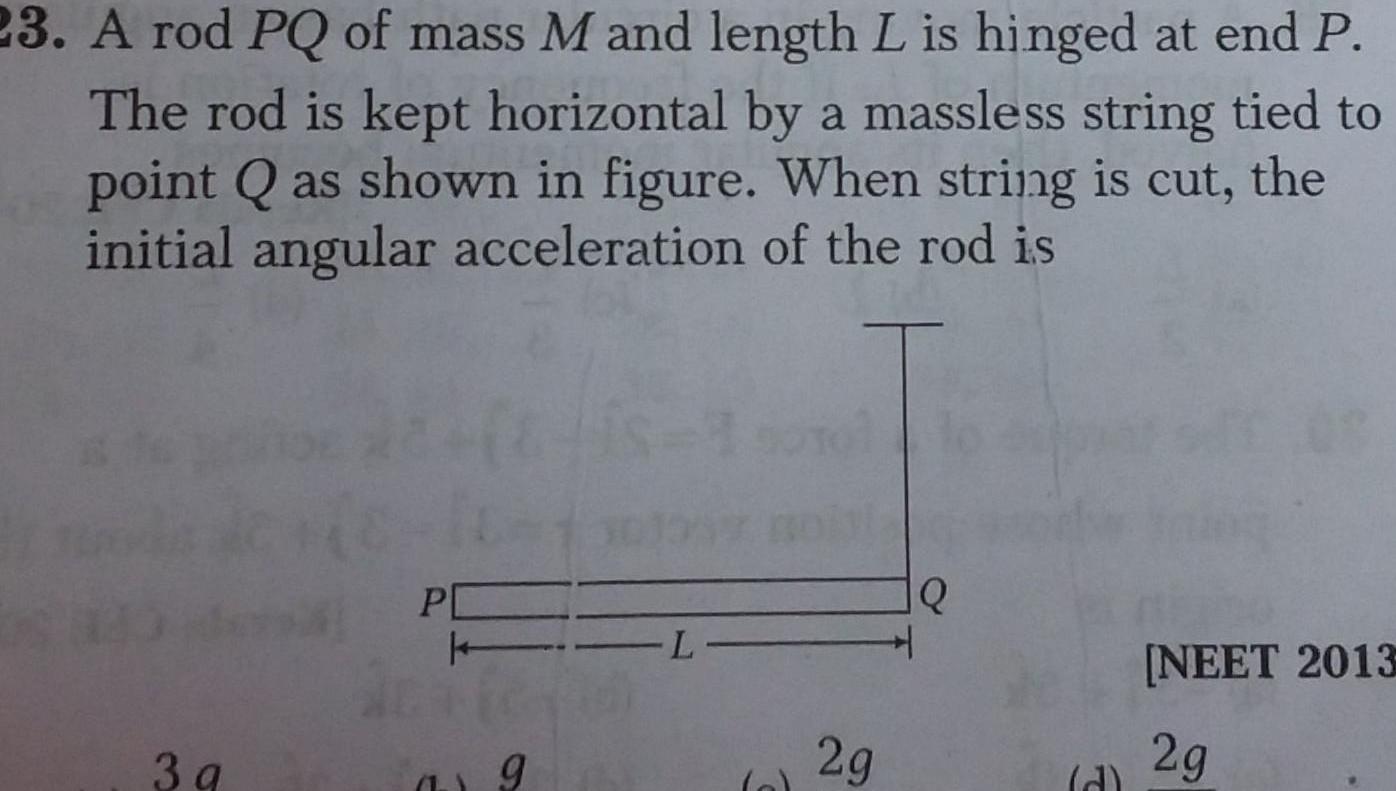
Physics
Rotation23 A rod PQ of mass M and length L is hinged at end P The rod is kept horizontal by a massless string tied to point Q as shown in figure When string is cut the initial angular acceleration of the rod is 3g PC k a 9 L o 2g Q d NEET 2013 2g

Physics
RotationNEET PHY Q 21 A hollow sphere is released from the top of a wedge as shown in the figure There is no friction between the wedge the ground There is sufficient friction to provide pure rolling The velocity of the sphere just before it leaves the wedge will be Assume Masses of the wedge and sphere are equal h R to be the radius of sphere Om 1 3gh 7 h m 2 49h 3 gh 6 6

Physics
RotationA ring of radius 0 25 metre and mass 10 kg rotating about its diameter with angular spe 40 rad s Its kinetic energy is 1 5 J 2 50 J 3 250 J 4 500 J
Physics
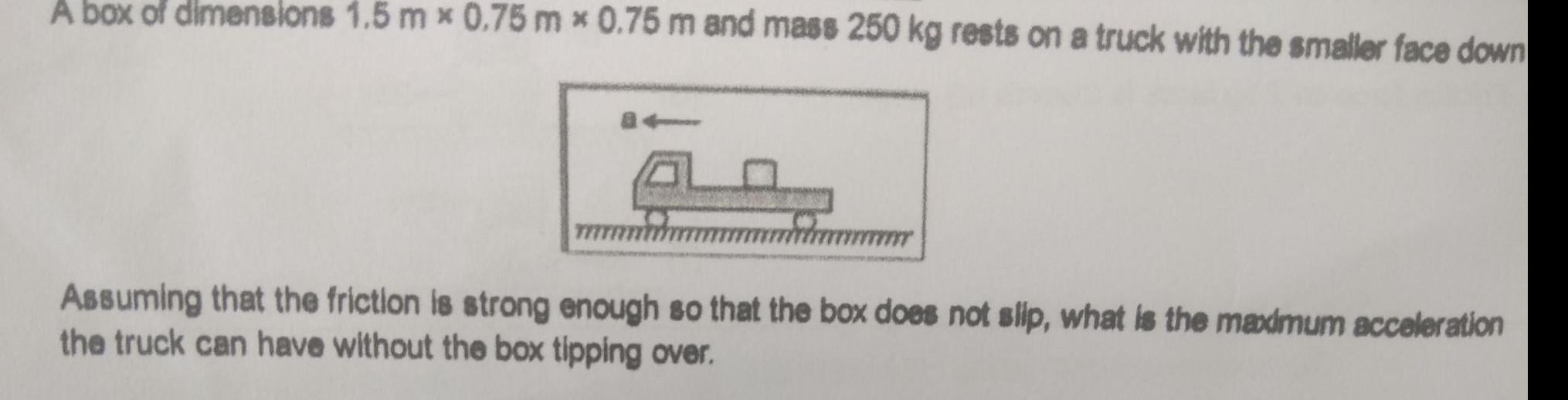
RotationA box of dimensions 1 5 mx 0 75 mx 0 75 m and mass 250 kg rests on a truck with the smaller face down Assuming that the friction is strong enough so that the box does not slip what is the maximum acceleration the truck can have without the box tipping over
Physics
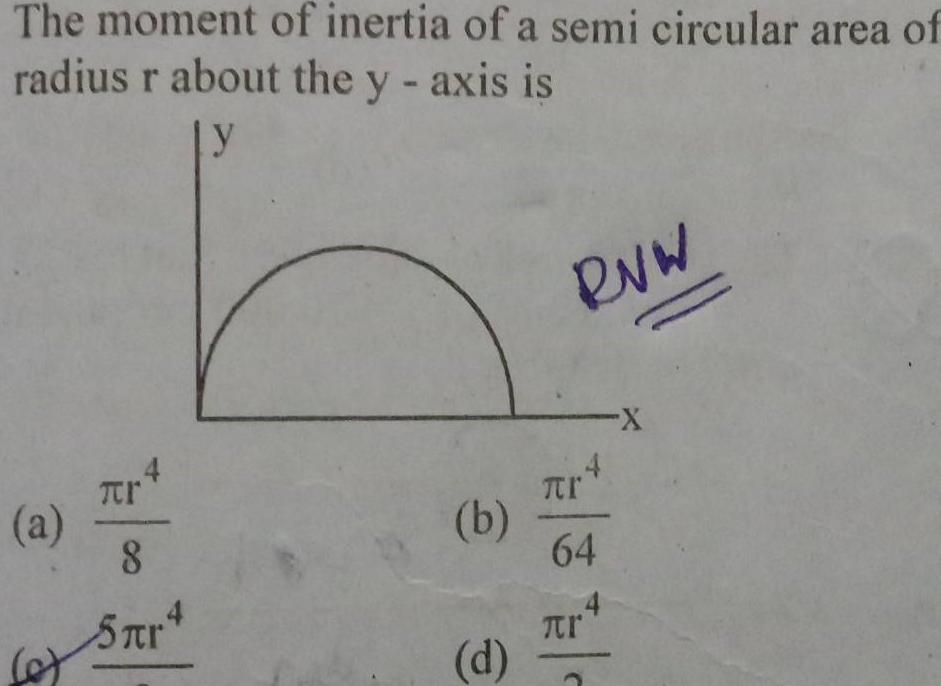
RotationThe moment of inertia of a semi circular area of radius r about the y axis is Ly c Tr 8 5 r4 b d RVW TI 4 64 r X

Physics
RotationExample 9 46 A horizontal force F acts on the hollow sphere at its centre as shown Coefficient of friction between ground and sphere is u What is maximum value of F for which there is no slipping O F f force of friction

Physics
RotationIn the adjacent figure a light and thin string is wound on a uniform disc of mass m and radius r very tightly The disc is kept at rest in vertical position on a rough horizontal surface and string passes over a fixed pulley A light pan is attached to the free end of the string The maximum mass that can be placed on the pan so that disc will not slip s equal to mK 2 Find K coefficient of friction between the surface nd the disc is 0 1 and there is no friction between string and pulley disc
Physics
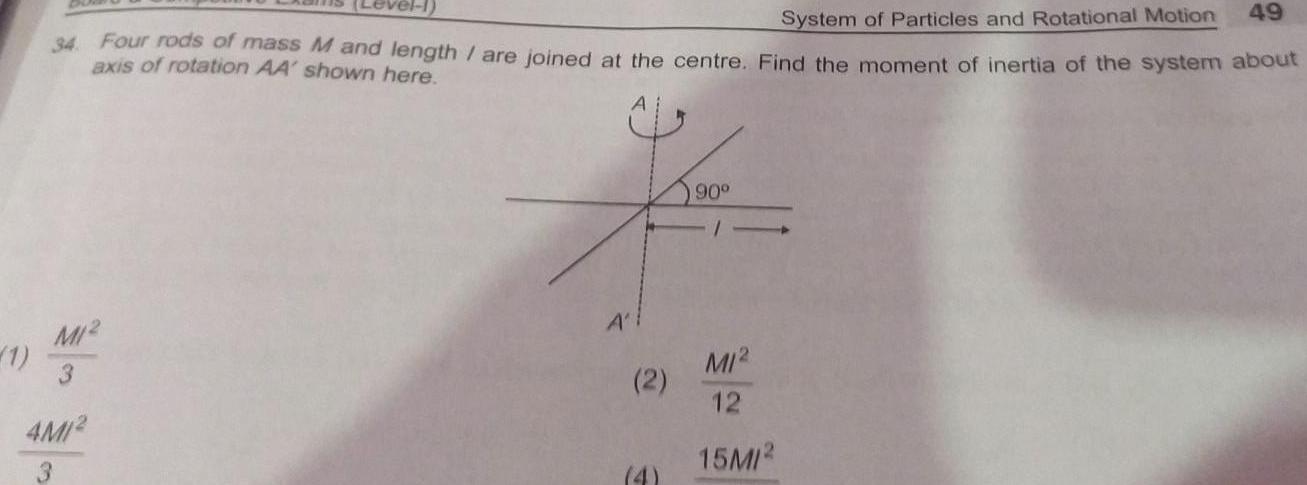
Rotation49 System of Particles and Rotational Motion 34 Four rods of mass M and length are joined at the centre Find the moment of inertia of the system about axis of rotation AA shown here M12 3 4M12 1 A 2 90 M1 12 15M

Physics
RotationD In Column I situations are given in which a constant force starts acting on a body initially at rest on a rough horizontal surface Match with the observations given in Column II Column I Column II A B C D Ring d Disc 5 Solid Sphere Solid Cylinder F F P 9 R S Body accelerates forward Rotation about the centre of mass is clockwise lo cudrom Friction force acts backward No friction acts 2 Rotational M

Physics
RotationComprehension 3 The general motion of a rigid body can be considered to be a combination of i a motion of its centre of mass about an axis and ii its motion about an instantaneous axis passing through the centre of mass These axes need not be stationary Consider for example a thin uniform disc welded rigidly fixed horizontally at its rim to a massless stick as shown in the figure When the disc stick system is rotated about the origin on a horizontal frictionless plane with angular speed the motion at any instant can be taken as a combination of i a rotation of the centre of mass of the disc about the z axis and ii a rotation of the disc through an instantaneous vertical axis passing through its centre of mass as is seen from the changed orientation of points P and Q Both these motions have the same angular speed in this case 5 P 6 Z I Now consider two similar systems as shown in the figure Case a the disc with its face vertical and parallel to x z plane Case b the disc with its face making an angle of 45 with x y plane and its horizontal diameter parallel to x axis In both the cases the disc is welded at point P and the systems are rotated with constant angular speed about the z axis Q P Z 45 y Case a Case b Which of the following statements about the instantaneous axis passing through the centre of mass is correct 2012 y A It is vertical for both the cases a and b B It is vertical for case a and is at 45 to the x z plane and lies in the plane of the disc for case b C It is horizontal for case a and is at 45 to the x z plane and is normal to the plane of the disc for case b D It is vertical for case a and is 45 to the x z plane and is normal to the plane of the disc for case b B It is for case a and D It is m for h Which of the following statements regarding the angular speed about the instantaneous axis passing through the centre of mass is correct 2012 A It is 200 for both the cases C It is for case a and 2 for case b 0 for case b
Physics
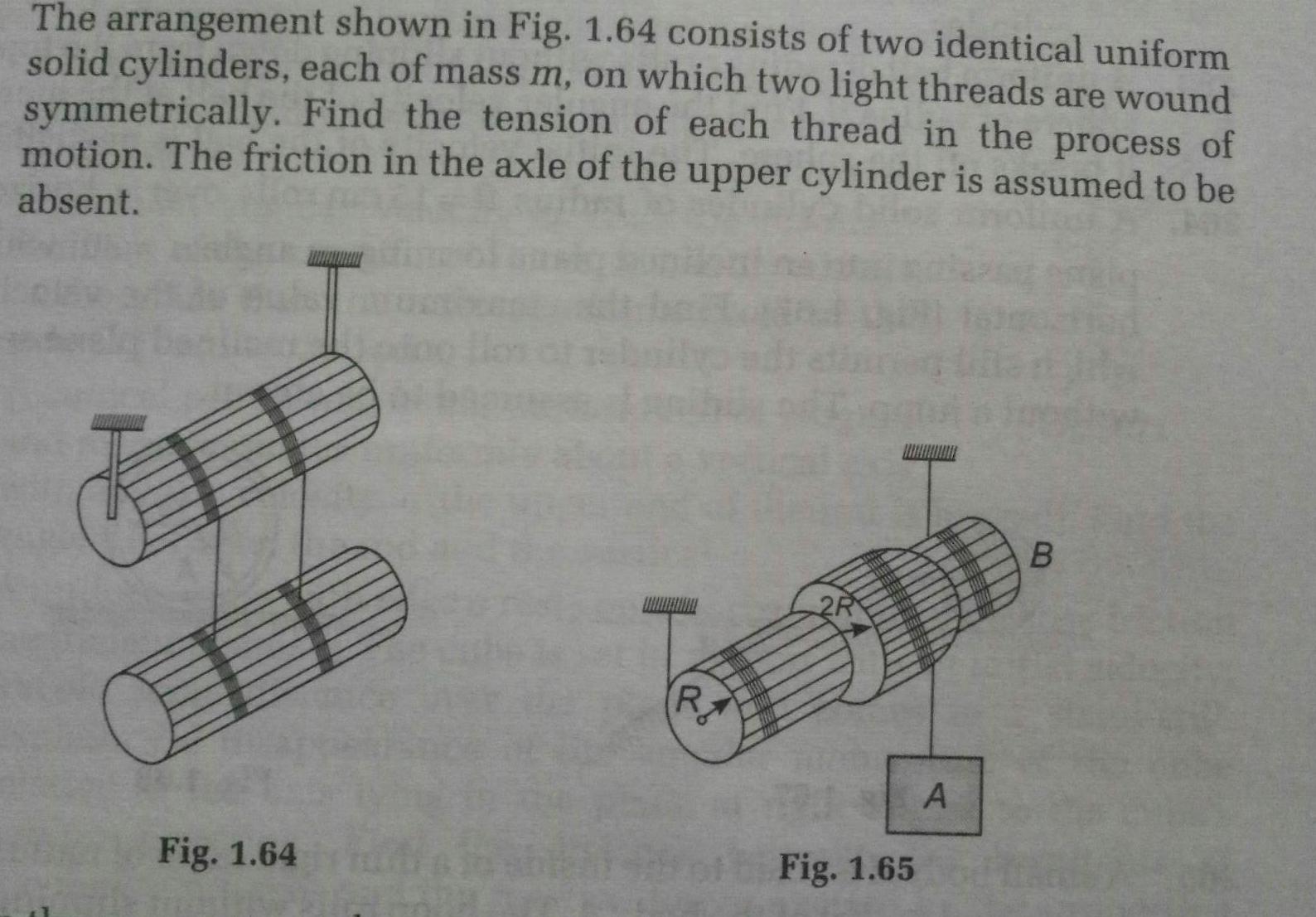
RotationThe arrangement shown in Fig 1 64 consists of two identical uniform solid cylinders each of mass m on which two light threads are wound symmetrically Find the tension of each thread in the process of motion The friction in the axle of the upper cylinder is assumed to be absent Fig 1 64 R 2R TORE BER TIME HOME THE Fig 1 65 N A B

Physics
RotationA weightless ladder 20 ft long rests against a frictionless wall at an angle of 60 with the horizontal A 150 pound man is 4 ft from the top of the ladder A horizontal force is needed to prevent it from slipping Choose the correct magnitude from the following a 175 lb b 100 lb d 150 lb c 70 lb
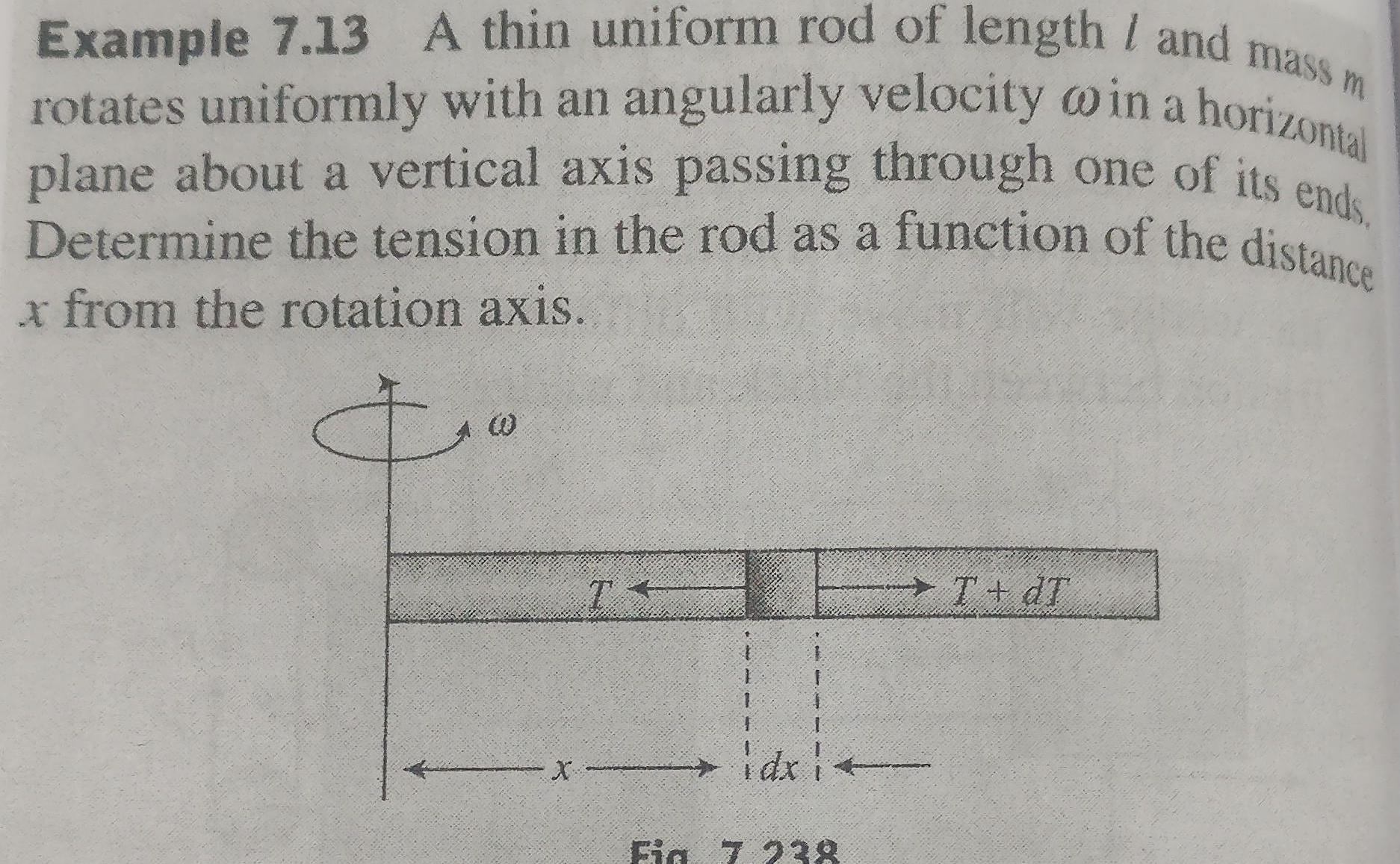
Physics
RotationExample 7 13 A thin uniform rod of length and mass m rotates uniformly with an angularly velocity in a horizontal plane about a vertical axis passing through one of its ends Determine the tension in the rod as a function of the distance x from the rotation axis X idxi Fig 7 238 T dT
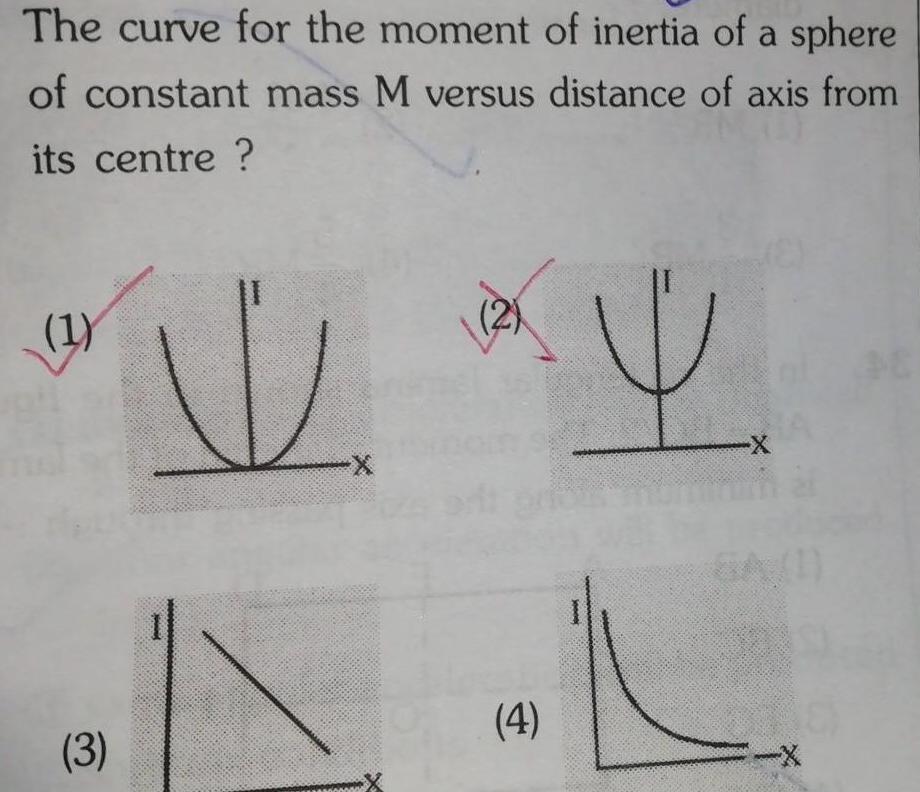
Physics
RotationThe curve for the moment of inertia of a sphere of constant mass M versus distance of axis from its centre 1 3 Hind V X 2 4 X
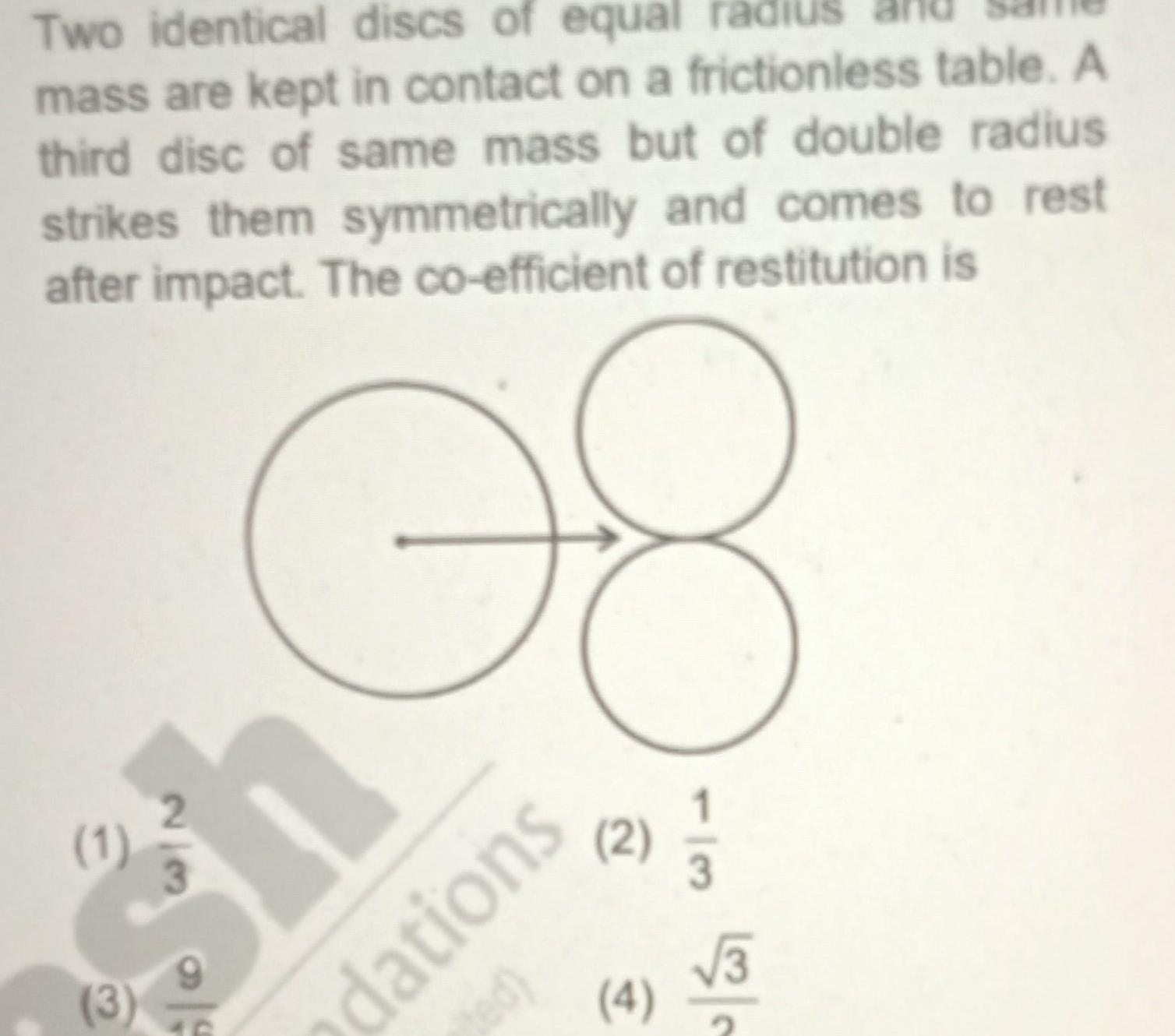
Physics
RotationTwo identical discs of equal radiu mass are kept in contact on a frictionless table A third disc of same mass but of double radius strikes them symmetrically and comes to rest after impact The co efficient of restitution is 08 1 3 3 us dations ted 2 1 1 2 3 4

Physics
Rotation18 The surface density of a circular disc of radius a depends on the distance as p r A Br The moment of inertia about the line perpendicular to the plane of the disc is A 2a 3 c 2 a 2 5 B A Ba 2 5 A b a 4 2B 2 5 d None of these

Physics
RotationWrite down the relation between torque and angular momentum Write down the principle of conservation of angular momentum Define moment of inertia State the theorem of perpendicular axes Define Poisson s ratio What are its limiting values 2 1 1 2
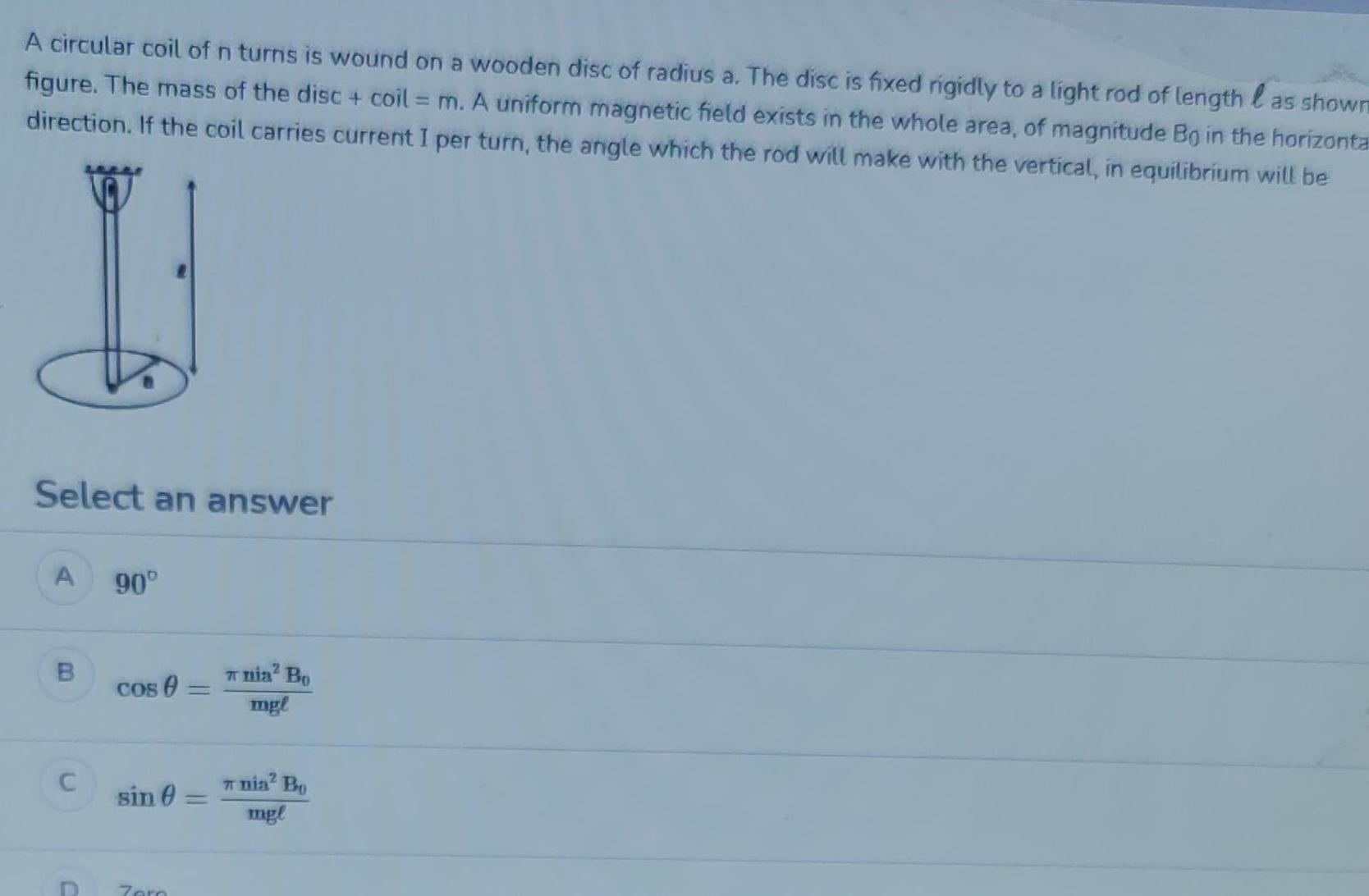
Physics
RotationA circular coil of n turns is wound on a wooden disc of radius a The disc is fixed rigidly to a light rod of length as shown figure The mass of the disc coil m A uniform magnetic field exists in the whole area of magnitude Bo in the horizonta direction If the coil carries current I per turn the angle which the rod will make with the vertical in equilibrium will be Select an answer A B C D 90 Cos sin Zero nia Bo mgl nia Bo mgl

Physics
Rotationportion of diameter R is cut out from a uniform circular disc of mass M and radius R as shown in figure The moment of inertia of the remaining shaded portion of the disc about an axis passing through the centre O of the disc and perpendicular to its plane is RR 15m Cut out portion 1 MB 13 3 MR 4 MR

Physics
RotationA small mass atta to a string rotates on a frictionless table top as shown If the tension in the string is increased by pulling the string causing the radius of the circular motion to decrease by a factor of 2 the kinetic energy of the mass will r 1 Decrease by a factor of 2 2 Remain constant 3 Increase by a factor of 2 4 Increase by a factor of 4

Physics
RotationThe instantaneous angular position of a point o a rotating wheel is given by the equatio 0 t 2t3 6t The torque on the wheel become zero at 1 t 1s 3 t 0 25 s 2 t 0 5 s 4 t 2s

Physics
RotationThe moment of inertia of a thin uniform rod of mass M and length L about an axis passing through its midpoint and perpendicular to its length is Io Its moment of inertia about an axis passing through one of its ends and perpendicular to its length is 1 Io ML2 2 2 Io ML2 4 3 Io 2ML2 4 In MI 2
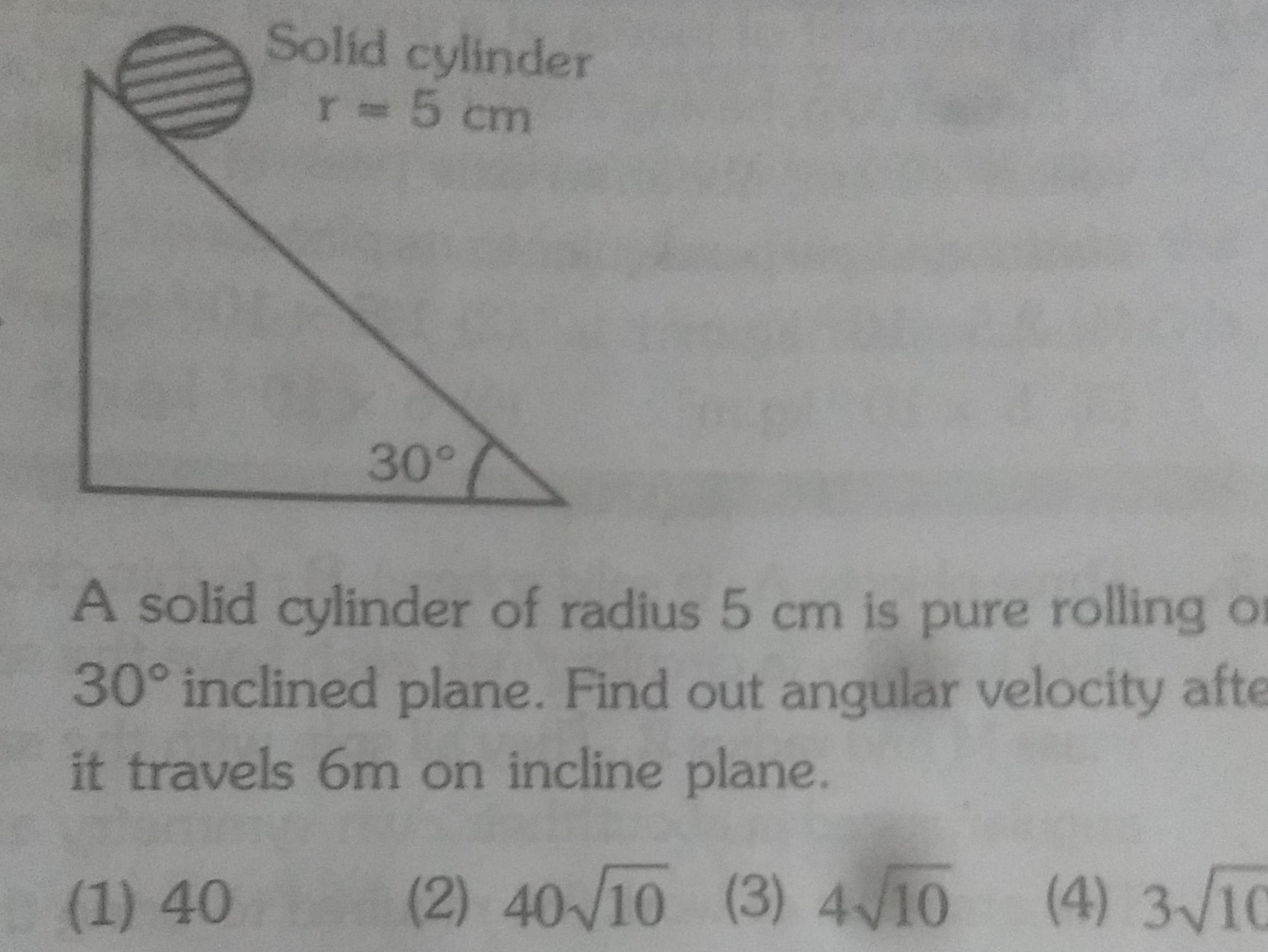
Physics
RotationSolid cylinder r 5 cm 30 A solid cylinder of radius 5 cm is pure rolling o 30 inclined plane Find out angular velocity afte it travels 6m on incline plane 1 40 2 40 10 3 4 10 4 3 10

Physics
RotationThe ratio of the accelerations for a solid sphere mass m and radius R rolling down an incline of angle 0 without slipping and slipping down the incline without rolling is 1 5 7 3 2 5 2 2 3 4 7 5 159

Physics
Rotation1 A rope is wound around a hollow cylinder of mass 3 kg and radius 40 cm What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N 1 0 25 rad s 3 5 m s 2 25 rad s 4 25 m s
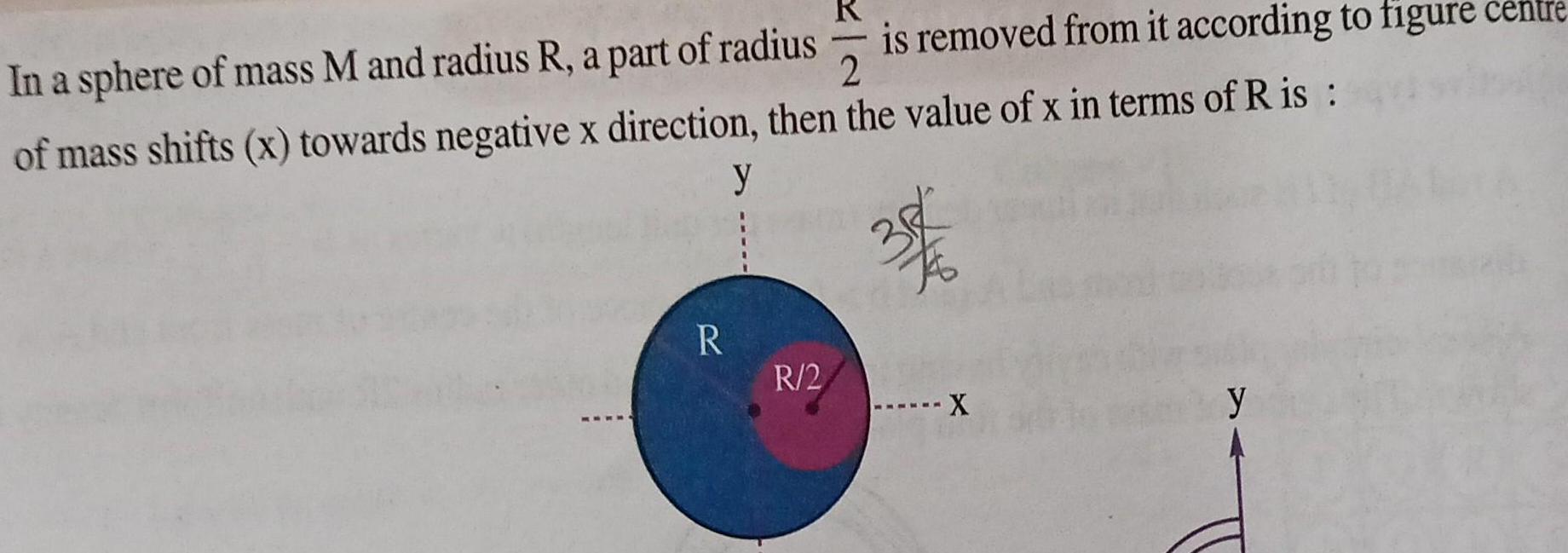
Physics
RotationR In a sphere of mass M and radius R a part of radius 2 of mass shifts x towards negative x direction then the value of x in terms of R is y 36 R 2 is removed from it according to figure centre X y

Physics
Rotation2 Assertion A cyclist bends inwards from his vertical position while turning to secure the necessary centripetal force Reason Friction between the tyres and road provides him the necessary centripetal force

Physics
RotationThree concentric conducting spherical shells carry charges as follows 4Q on the inner shell 2Q on the middle shell and 5Q on the outer shell The charge on the inner surface of the outer shell is 1 0 3 O 2 4 Q 4 20

Physics
RotationA force F k acts at origin then torque of the 10 force w r t to point 1 1 is 1 F i j 3 F i j 2 F i j 4 F i j fara a forg k 11 1 F i j 3 F i j 2 F i j 4 F i j
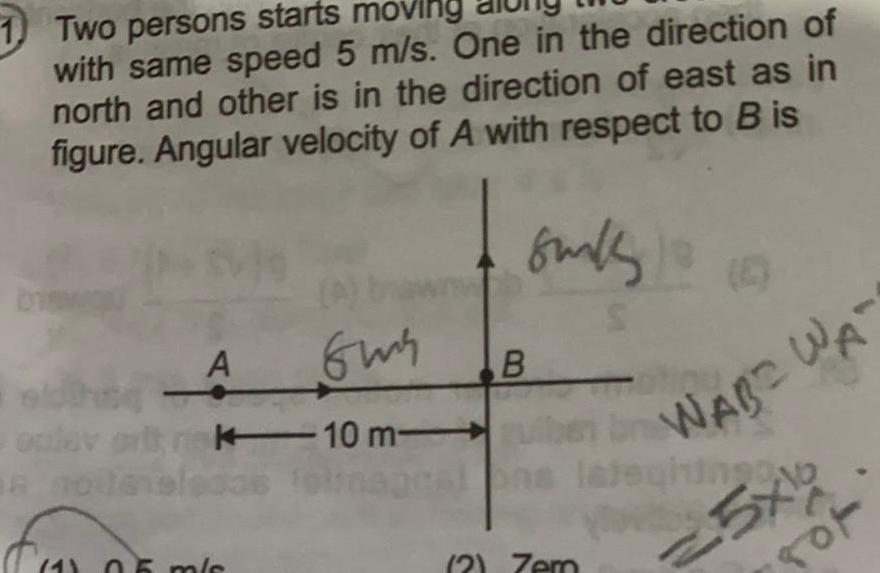
Physics
RotationTwo persons starts moving with same speed 5 m s One in the direction of north and other is in the direction of east as in figure Angular velocity of A with respect to B is A Gus This lav pritrk 10 m ledas 8 00 4 0 6 m s sunk S B WABE WA heal ons latehingg 2 Zem 5x10 of

Physics
RotationA dog of mass m is walking on a pivoted disc of radius R and mass M in a circle of radius R 2 with an angular frequency n the disc will revolve in opposite direction with frequency Y FLA 22 1 izt 1 3 mn M 2mn M R 2 2 AL 42 FXLX 79 mn 2M e d 2 FX 2 L X 2Mn 4 M 5am and b 20cm If the M I of the

Physics
Rotation7 A particle moves with a constant velocity parallel to the X axis Its angular momentum with respect to the origin 1 is zero 3 goes on increasing 2 remains constant 4 goes on decreasing
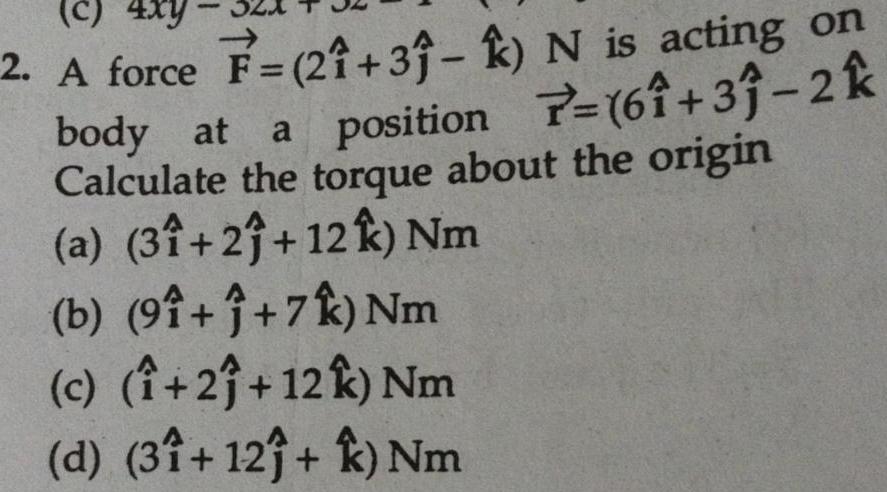
Physics
Rotationc 4xy 2 A force F 21 31 k N is acting on body at a position 7 61 31 2k Calculate the torque about the origin a 31 2 12 k Nm b 91 1 7k Nm c 21 12 k Nm d 31 12 k Nm
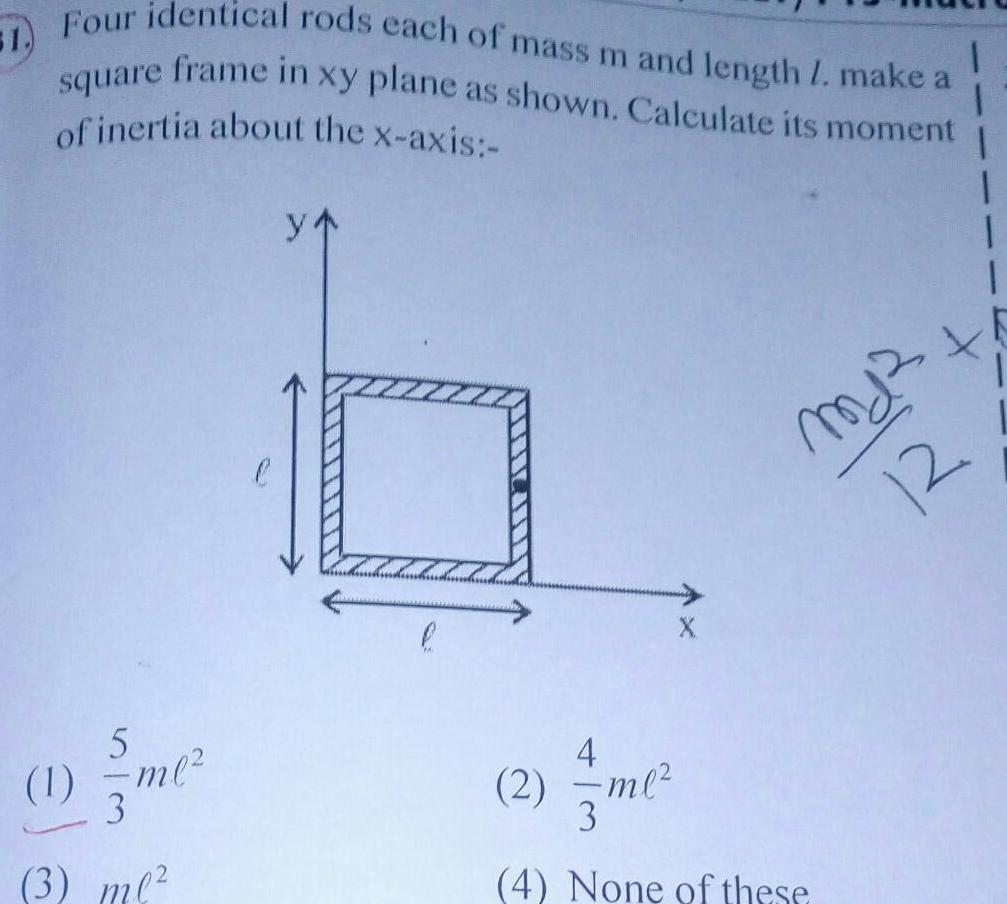
Physics
Rotation51 Four identical rods each of mass m and length 1 make a frame in xy plane as shown Calculate its moment square of inertia about the x axis 5 1 3me 3 ml y 7 C md 12 4 2 ml 7me 3 4 None of these 1 1

Physics
RotationA uniform disc of radius R and mass m lies on a smooth horizontal plane A ring of mass 2m and radius R 2 spinning with angular velocity wo is carefully lowered onto the disc such that centre of disc and centre of the ring coincide The coefficient of friction between them is Then which of the following is INCORRECT A The time when both disc and ring spin with the same angular velocity is R R B The time when both disc and ring spin with the same angular velocity is 2 g C The final angular velocity of disc becomes D The final angular velocity of ring becomes o 2 4 g 2

Physics
RotationTwo wheels P and Q are mounted on the same axle The moment of inertia of P is 6 kg m2 and it is rotating at 600 rotations per minute and Q is at rest If the two are joined by means of a clutch then they combined and rotate at 400 rotations per minute The moment of inertia of Q will be A 3 kg m B 4 kg m C 5 kg m D 8 kg m

Physics
RotationA pulley is hinged at the centre and a massless thread is wrapped around it The thread is pulled with a constant force F starting from rest As the time increases F K ABAL 1 its angular velocity increases but force on hinge remains constant 2 its angular velocity remains same but force on hinge increases 3 its angular velocity increases and force on hinge increases 4 its angular velocity remains same and force on
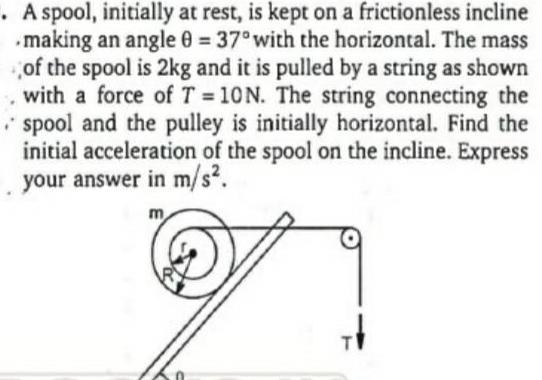
Physics
RotationA spool initially at rest is kept on a frictionless incline making an angle 0 37 with the horizontal The mass of the spool is 2kg and it is pulled by a string as shown with a force of T 10N The string connecting the spool and the pulley is initially horizontal Find the initial acceleration of the spool on the incline Express your answer in m s m T
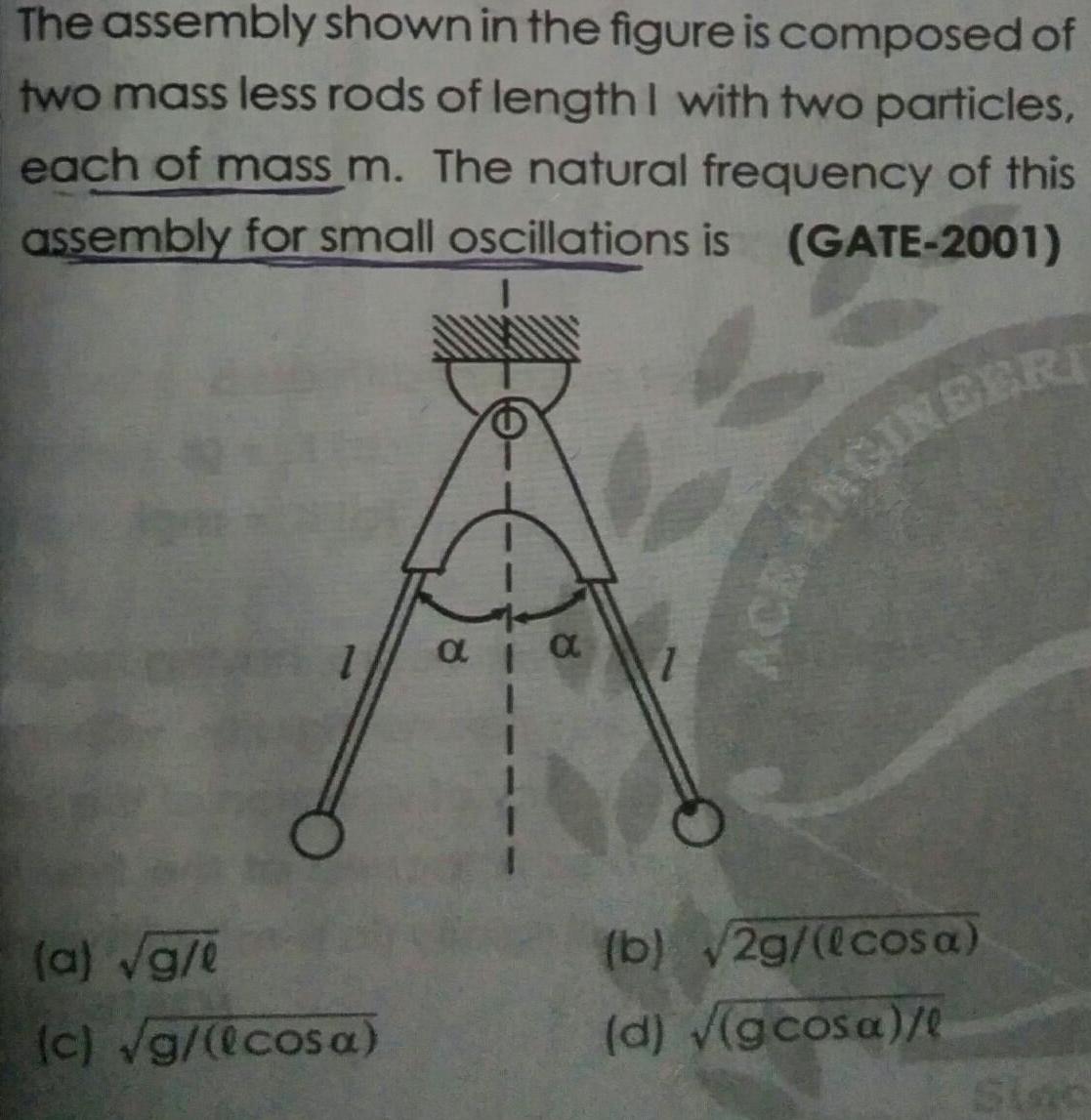
Physics
RotationThe assembly shown in the figure is composed of two mass less rods of length I with two particles each of mass m The natural frequency of this assembly for small oscillations is GATE 2001 a g l c g cosa a 1 b 2g lcosa d gcosa l CE ENGINEERI
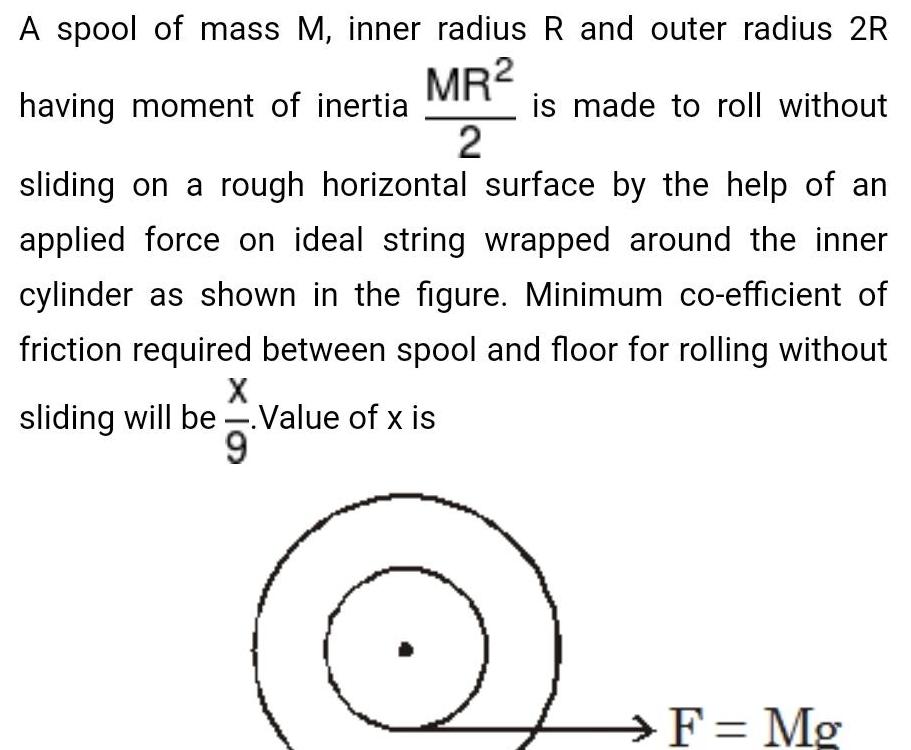
Physics
RotationA spool of mass M inner radius R and outer radius 2R MR having moment of inertia 2 sliding on a rough horizontal surface by the help of an applied force on ideal string wrapped around the inner cylinder as shown in the figure Minimum co efficient of friction required between spool and floor for rolling without X sliding will be Value of x is 9 is made to roll without F Mg

Physics
Rotationirst decreases and then increases A 25 kg uniform solid sphere with a 20 cm radius is suspended by a vertical wire such that the point of suspensic vertically ab ove the centre of the sphere A torque of 0 10 N m is required to rotate the sphere through an angl 1 0 rad and then maintain the orientation If the sphere is then released its time period of the oscillation will be 1 second 3 2 second 2 2 second 4 4 second 2 2 0r1 0

Physics
RotationWhich of the following statement is wrong Torque in rotational motion is analogue to force in linear motion Couple acting on an object can produce linear acceleration For an extended body centre of mass and centre of gravity may not coincide Rolling motion is combination of linear and translation motion

Physics
RotationA homogenous cylinder of mass M and radius R is pulled on a horizontal plane by a horizontal force F acting through its centre of mass Assuming pure rolling angular acceleration of cylinder will be O O 2F 3MR 3F 2MR F 3MR