Lise Matematik Soruları

LA) 200 x. 08075 11. Buğdaydan ağırlığının % 40' (kadar un, undan da ağır- liğinin % 80 fazlası kadar hamur elde edilmektedi Buna göre, 180 kg hamur elde etmek için kaç kg buğday gereklidir? B) 250 122 (0 10.80 C) 300 D) 350 100 a E) 400 $ 2

receden Denklemler 5. GÖKBEY, Türkiye'nin yerli imkanlarla geliştirip ürettiği ilk ge Şekilde, GÖKBEY'in I numaralı pistteki T noktasından kalkış yaptıktan sonra II numaralı pistteki R noktasına indiği ana nel maksatlı helikopteridir. kadar havada izlediği yol gösterilmiştir. T 1. pist x² h(x) = x - 20 A) 3 Test 109 II. pist T noktasından kalkış yaptıktan sonra helikopterin yerden yüksekliği h (km), yatayda aldığı mesafe x (km) olmak üzere h ile x arasındaki ilişki 2x = x² B) 5 X=22 C) 6 R eşitliği ile modellenmiştir. Buna göre, helikopterin hareketi boyunca yerden yük- sekliği en fazla kaç km olmuştur? Nesli tükenme adaya 2000 y t yıl sonra ad p(t) = t²-4t şeklinde Buna göre sayısında 8. D) 7 E) 8 Ok ÖSYM Tar A) 21 9. mc

02. Kesişen iki doğruda oluşan açılardan komşu olma- yan açılara ters açılar denir. Ters açılanın ölçüleri birbirine eşittir. A 2x+20 x+35 D Şekilde AOD açısı ile BOC açıları ters açılardır. Buna göre x kaçtır? A) 15 B) 20 C) 25 D) 30

i bar- suyun e endemik 0.2.06 01.03 08.48 00.54 26. Biri saatte 3 dakika ileri giden, diğeri saatte 6 dakika geri kalan analog iki saat vardır. Buna göre her iki saat doğru zamanı gösterdikten en az kaç gün sonra tekrar doğru zamanı gösterir? A) 5 B) 10 C) 15 D) 20 E) 30 3691218 6 12 18.24 30 36 42 48 54 60 56+x 8 27. Bir kireç taşı heykel, mermer bir heykelden 56 yaş daha Üç sayının sayıların Bu üç sa büyük o A) 25 30. Satir, pinde

Q+B3 3K 6 A) 6 K+2k 13. Bir işi Büşra tek başına 2a saatte, aynı işi Ceren tek başına 3b saatte yapabiliyor. is 6C a b-6a9b 4 →3k olduğuna göre bu işi Büşra ile Ceren birlikte kaç saatte yapabilirler? B) 9 C) 12 D) 15 E) 18

3445k ve 5. Birer sayı belirten doğru orantılıdır. Buna göre kaçtır? A) 11 4.A +3. A) 15 10.6 sırasıyla 3 ve 5 ile ifadesinin değeri B) 12 C) 13 4.34 +3.5/ 1242484 24 274 a2 D) 14 6. Aşağıda verilen tablolardan hangisindeki orantı sabiti diğerlerinden farklıdır? 26235 u 2 8 6 10 12 30

8 6. M-2 (x + 1) - [(m - 2)x² - 6x + m - 10] = 0 denkleminin gerçek sayılardaki çözüm kümesi iki eleman lıdır. Buna göre, m'nin alabileceği değerlerin toplamı kaçtır? A) 5 B) 11 18 C) 13 D) 15 E) 16 ok 9. 7. Aşağıda çevre uzunlukları birbirine eşit olan eşkenar üçgen x²-5 denkler ifadesi A) 9

ERNEK -6-3-1 O dinat sistemind zerinde olan di çevreleri t 13. 20 IAOI = 2.1OBI olduğuna göre, m kaçtır? 4 2 k y=-x² - 4x + m + 6 parabolünün grafiği yukarıda verilmiştir. 1--2 -8.4=476 -1 -32=²²6 26=m B X 16. f fonksiyon 17.

5-12- 3 42 42 --2 dakiler. 2x + 20 x + 20 23. A F(x)= 0.(x+1). (X-5) ((x) = -5 a 5=-5a a=-1 f(x) Şekilde OABC karesinin B kişesi f(x) parabolünün tepe noktasıdır. Alan(OABC): = 4 birimkare Buna göre, f(6) değeri kaçtır? A) 2 B) 3 C) 4 D) 5 E) 6 8

1000 arklı iye HOCALARA GELDİK 28. A 9 9x=11y. " lom A noktasındaki tırtıl B'ye ve B noktasındaki tırtıl A'ya en kısa yoldan gitmek üzere aynı anda A ve B noktasın- dan aynı anda hareket edi- yorlar. B'deki tırtılın hızı, A'daki tırtılın hızının 3 katıdır. İki tırtıl şekildeki çizgilerin üzerinden hareket ettiklerine göre, buluşma olasılıkları kaçtır? A) 2/2 B) 1/2 C) 1/1/2 E) 1/14 3 4 D) gom gg goilo 24

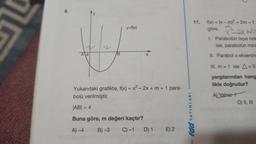
8. Ao y=f(x) Yukarıdaki grafikte, f(x) = x² - 2x + m + 1 para- bolü verilmiştir. |AB| = 4 Buna göre, m değeri kaçtır? A)-4 B)-3 C) -1 D) 1 E) 2 YAYINLARI 11. - fdd T 2 f(x) = (x - m)² + 2m - 1 göre, 2X - I. Parabolün tepe nok ise, parabolün mini II. Parabol x eksenine III. m = 1 ise A<0 yargılarından hang likle doğrudur? A) Yalnız D) II, III

DGS DENEME SINAVI / SAYISAL Mert ve Çiğdem kendi aralarında aşağıdaki kurallara göre, tavla oynamaktadırlar. Tavla 2 zar ve 15 pulla oynanmaktadır. Pulların tamamını rakibinden önce toplayan oyu- nu kazanmaktadır. 27-28. SORULARI AŞAĞIDAKİ BİLGİLERE GÖRE CEVAPLAYINIZ. ● ÖRNEK: 2 kez MARS bir kez NORMAL oyun alan bir yarışmac 5 puan alarak rakibini yener. A) 5 Oyunculardan biri hiçbir pul alamadan diğer oyun- cu bütün pulları toplayarak kazanırsa 2 puan ka- zanılır ve bu oyuna MARS denir. Mars dışındaki oyunlara NORMAL sonuç denir ve 1 puan kazanılır. 3 kez MARS yapan bir yarışmacı 6 puan alarak rakibini yener. 005 EF Tavla oyununda 5 veya 6 puana ilk ulaşan oyunu kazanır. Mert A) 14 27. Mert en çok kaç oyun oynayarak Çiğdem'i yenebilir? ci B) 6 B) 13 5.1 11111 → 1 11123 12273" 7 C) 7 28. Mert hiç oyun almadan Çiğdem, Mert'i kaç farklı bi- gimde yenebilir? 12+779 TASARI EĞİTİM YAYINLARI Giden C) 12 D) 8 E) 9 D) 9 TASARI EĞİTİM YAYINLARI E) 8 6 Pl 22.2 71° 11112-5. 29-30. SORULARI AŞAĞIDAKİ CEVAPLAYINIZ. A ve B GSM operatörleri aboneleri dikleri tutar ve 100 kontörle konuş gibidir. 11:22 21 64²-6 21.41 8 Kontör fiyatı Konuşma süresi bu 12 29. A şirketi 100 kontörle konuşma s 100 kontörle konuşma fiyatını da 2p. 60 Top A) 80 Buna göre, A operatörü bir dak yüzde kaç zam yapmıştır? B) 90 A operatör 20 TL 80 dak, 86-2 fode 64 de. 31 700 = 12 54 30. operatörü 100 kontörün fiya B operatörü bir dakikalık kc uygulayabilmesi için, 100 k deki değişimi nasıl olmalıdı 20t 324 A) %20 azaltmalı C) %30 azaltmalı C) 100 E) %25

9. a²b + ab² + 2a + 2b 4 ifadesinin çarpanlara ayrılmış biçimi aşağıdaki- lerden hangisidir? A) (a - b)(a + 2) C) (a + 2)(b + 2) B) (a + b)(b + 2) D) (a - b)(ab + 2) E) (a + b)(ab + 2) ol 21916 Verile silip topla A) 2x

C 2. 8 öğretmen ve 48 öğrenciden oluşan bir topluluk müzeye gezi düzenlemiştir. Müzenin öğrenci grupları için kuralları şu şekildedir. » Bir grup en az 4 ve en çok 8 kişiden oluşabilir. > Öğrenci gruplarının başında sadece 1 öğretmen bulu- nur ve bu öğretmenlerden ücret alınmaz. Bu müzede öğrenci bileti 10 TL öğretmen bileti 8 TL'dir. Buna göre, bu topluluk müzeye en az kaç TL öder? A) 496 D) 480 B) 488 E) 476 C) 484 4.

1 3. A) f(x) = B) f(x) 14 C) f(x) D) f(x): Yukarıda grafiği verilen y = f(x) fonksiyonu aşağıdakilerden hangisi olabilir? = -{X-²/2 -2 = (x+2 = E) f(x) = X-2 2 { 2 7 X-2 *F2 3 " 2 1 " x + 2, AY 1 3 15-x) = (1 X≥ 0 x < 0 X>0 X≤0 X≥0 x < 0 →y = f(x) X>0 x≤0 -X X ≤0 x≥0

1. 5 farklı fizik, 2 farklı kimya ve 3 farklı matematik kitabı bir rafa matematik kitapları sağ başta bir arada olmak şartıyla kaç farklı şekilde sıralanır? A) 5!.3! B) 81.3! C) 61.3! nie D) 71.3! E) 8!