Lise Matematik Soruları

3. A) {(0,3)} 2=uy 2x²=27 x²=9 X=3 (B) (3, 0)) D) {(4, 3), (3, 0)) 4x² + 3y² = 36 x² + 3y² = 9 denklem sisteminin çözüm kümesi aşağıdakilerden han- gisidir? X:-) vi HIZ YAYINLARI 11. SINIF MATEMATİK heleboti sinley (A E ((0, 3), (3, 0)) **** = C) (43)} 6

Altın oran doğada çokça rastladığımız bir çok bilimsel ve sanatsal alanda kullanılan görsellik ve işlevsellik açısın- dan olumlu bir etki oluşturan oransal bağıntıdır. Bir dikdörtgenin kısa kenar uzunluğu kullanılarak kare çizilip ve bunu devam ettirerek uzun kenarın kısa kena- rına oranının eşit olduğu dikdörtgenlerden oluşan şekle altın dikdörtgen denir. ABCD dikdörtgeninin AB kenan kullanılarak ABFE ka- resi çizilmiş ve bu işlem devam ettirilerek aşağıdaki altın dikdörtgen oluşturulmuştur. A B A) 1+√5 |MF|=|FG| = 1 br |GC| = |HC| = x br olduğuna göre, |AB| kaç birimdir? D) B) E 3+√5 2 F 1 G 2+√5 2 E) 3+√5 C) 2+√5

5. y=x²-3x+n+1 A)-1 y=x-1 00 denklem sistemini sağlayan bir tane (x, y) sıralı ikilisi ol- duğuna göre, n kaçtır? X x B) 0 x²ux+n+2 16 22 -2 C) 1 -2 Tabieloru D) 2 n=2 odliteb 512=32 E) 3 n² tun-r=0 ^

-X -X 5. Aşağıda y = f(x) fonksiyonunun grafiği verilmiştir. -6 3 B) 4 2 O -1 -2 1 Buna göre, y = f(x) fonksiyonunun minimum $noktasının apsisi maksimum noktasının apsi- sinden kaç fazladır? A) 5 3 4 5 C) 3 D) 2 E) 1

7. X = {0, 1, 2, 3, 4, 5, 6) kümesi veriliyor. X₂, X kümesinin 2 elemanlı bir alt kümesi . . X₁, X kümesinin 4 elemanlı bir alt kümesi olduğuna göre, X, UX, kümesinin elemanlar toplamı aşağıdakilerden hangisi olamaz? A) 10 ORTER A B) 11 2 C) 12 D) 19* 8. a ve b pozitif tam sayı olmak üzere, a (x² + 4y²)² mindak terimlerd ifadesinin açılımındaki terimlerden biri 2b.x².14 olduğuna göre, a + b tonlam E) 22 bigo

5. IS X13) Tole () x² - (m²-5m + 4)x+ 3-3m = 0 Buna göre, SX+6 denkleminin kökleri x, ve x₂ dir. X2 A) 5 B) 6 C) 7 X²-m²³²+ Sm+4. X₁Xx₂+ X₁ + X₂ ≤0 eşitsizliğini sağlayan kaç farklı m doğal sayısı vardır? D) 8 +3-3 1 8 E) 9

. Bir markette satılan kola, meyve suyu ve şişe suyunun paket satış fiyatları aşağıdaki gibi altlarına yazılmıştır. Şişe su Kola FLEEEEE 60 TL Meyve suyu 7,5 TL 30 TL Marketteki içecekleri müşteriler ister paket hâlinde isterse paketi yırtarak alabilmektedir. Bir gün içerisinde bu içeceklerden; satılan kolaların 5 sayısı, şişe sudan satılanların sayısının 2 suyundan satılanlanın sayısı ise şişe sudan satılarınların sayısının 3 katıdır. Market bir gün içerisinde bu içeceklerin satışından elde ettiği gelirin %8'ini KDV (Katma Değer Vergisi) olarak devlete ödemiş ve geriye 690 TL para kalmıştır. katı, meyve Buna göre, market bu içeceklerden bir gün içerisinde toplam kaç adet satmıştır? A) 250 1260 C) 270 D) 280 E) 290

novilites all tbl Opt from Davi M onigibnilld iğibilbs eble gues mül ev 3. Bir firmaya ait otobüs iki farklı şehir arasındaki yolu saatte 60 km hızla gidip aynı yolu saatte 90 km hızla dönmektedir. Buna göre bu otobüsün yol boyuncaki ortalama hızı koc km'dir? HL.

58 6. b ve c sıfırdan farklı gerçek sayı olmak üzere z²+bz+c=0 denkleminin karmaşık kökleri z, ve z₂ dir. Buna göre aşağıdakilerden hangisi kesinlikle doğru- dur? A) Z₁ > Z₂ B) Z₁ <Z₂ D) Z₁ = Z₂ C) Z₁ =-Z₂ E) z² = 2²2

adır. tir. He dan teke 200 5040 3. Bir okulun 9-A sınıfında 3, 9-B sınıfında 4 kişilik boş yer vardır. Aralarında Aykut ile Ridvan'ın bulunduğu 7 kişi bu okula kayıt yaptırmıştır. Ridvan ile Aykut aynı sınıfta olmamak şartıyla bu 7 öğrenci 9-A ve 9-B sınıflarına kaç farklı şekilde yerleştirilebilir? b A) 60 B) 40 71- 1 C) 20 D) 15 T E) 10 içecek Yalnız olacal A) 30 T ✓ 6

10 A daa. 28. Bir okulun 3 müdür yardımcışı ve 5 öğretmeni bir proje kapsamında 4 er kişilik ekipler halinde Prag ve Italya'ya gideceklerdir. Müdür yardımcılarının üçünün de aynı ekipte olmayacağı kaç farklı ekip oluşturulabilir? A) 36 B) 42 C) 48 16 12 D) 54 E) 60 31.

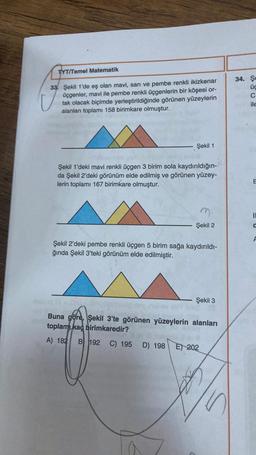
TYT/Temel Matematik 33 Şekil 1'de eş olan mavi, sarı ve pembe renkli ikizkenar üçgenler, mavi ile pembe renkli üçgenlerin bir köşesi or- tak olacak biçimde yerleştirildiğinde görünen yüzeylerin alanları toplamı 158 birimkare olmuştur. Şekil 1 Şekil 1'deki mavi renkli üçgen 3 birim sola kaydırıldığın- da Şekil 2'deki görünüm elde edilmiş ve görünen yüzey- lerin toplamı 167 birimkare olmuştur. Şekil 2 Şekil 2'deki pembe renkli üçgen 5 birim sağa kaydırıldı- ğında Şekil 3'teki görünüm elde edilmiştir. Şekil 3 DALE Buna göre, Şekil 3'te görünen yüzeylerin alanları toplamı kaç birimkaredir? A) 182 B 192 C) 195 D) 198 E) 202 34. Şe üc C ile E

+ A ÖGRETEN SORULAR Ho a=21 idion 13. a ve b birer gerçel sayı olmak üzere, -3 √3a-12 + √b+3 √16-4a+√5-b C = a B) 77 17 ↑ denklemini sağlayan b değeri kaçtır? 83 85 A) 11 C) 17 D) 95 E) 5 17 3 (0-4 Jucusa √3 (a-4) 3x - 3 137 $14 152 √3 ~A Su

1. C 2. B 3. C 4. E 5. D 6. E 7. E 8.B 9. B 10. D 11. D 12. E 13. D 14. D 15. A 16. E 13. n bir gerçek sayı olmak üzere, x² - (2n +1)x+ n²+ n-6=0 E) 11 ikinci dereceden denkleminin çözüm kümesi aşağıdakilerden hangisi olabilir? A) {1, n-2} C) {1+n, 2 + n} E) {-n-3, 2-n} B) {1, n + 3} D) {n-2, n + 3} İkinci De 1. Aşağ çift ka A)x² C) 4

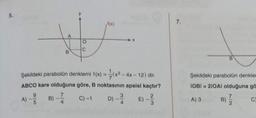
5. A) B B) O C Şekildeki parabolün denklemi f(x) = (x²- - 4x-12) dir. ABCO kare olduğuna göre, B noktasının apsisi kaçtır? 9 C) -1 f(x) D) 3 E) -- 3 7. B Şekildeki parabolün denkler IOBI=210Al olduğuna gö B) 7/7/2 A) 3 C

-g(x) Sear Fros! x²+3x-10 X- 3 3 ≤1 A) II ve III > 0 -5 4 D) Yalnız I O eşitsizlik sistemini sağlayan x in alabileceği, dört tane negatif tam sayı değeri vardır. -4-3-2-1 vardır en küçük pozitif tam sayı değeri 3 tür. 3 III. en büyük pozitif tam sayı değeri 4 tür. Yukarıdaki yargılardan hangileri doğrudur? B) I ve II ✓ + P + 33 E) I, II ve III C) Yalnız II