Permütasyon Soruları

E) 300 3 0 0 949 9993 65 33 (2,4₁) 18 23 35 45 53 sayı 16. Rakamları farklı üç basamaklı 5 ile tam bölünebi len kaç tane doğal sayı vardır? A) 118 B) 120 C) 124 D) 136 E) 148 10 13 14 15 16 B B E C D 56 9 C 11 A 12 E

1. Aşağıda bir hesap makinesinin taş takımı gösterilmiştir. Bu tuşlara basılarak 6 basamaklı sayılar oluşturuluyor. 1 2 3 4 5 6 7 8 9 Oluşturulacak altı basamaklı sayının ilk üç basamağı her bir satır ve sütun üzerinde sadece bir tuşa basılarak, son üç basamağı ise her satırda tuşlardan birine basılarak oluşturuluyor. Buna göre, rakamları farklı kaç sayı yazılabilir? A) 61 B) 5-6! D) 123 E) 6³-61 C) 6-6! Gamze Öner Gülmüş * Gamze Öner Gülmüş ner Gülmüs

5. 4 evli çift yan yana düz bir sıraya oturacaklardır. Evli çiftlerden sadece 3 çift birlikte bulunmak ve bu 3 evli çift yan yana oturmak şartıyla kaç farklı şekilde sıralanır? A) 144 B) 168 C) 142 D) 284 E) 384

ol- man 36 sun A B Yukarıdaki şekilde bir binanın 4 farklı giriş kapısı gösteril- miştir. Bu binaya gelecek olan 5 kiş yukarıda gösterilen 4 kapıdan girecektir. Her kapıdan en az bir kişi girmek koşuluyla bu 5 kişi binaya kaç farklı biçimde girebilir? A) 150 B) 200 C) 240 D) 260 E) 280 13. Bir iş yerinde biri 6, diğeri 5 kişilik olmak üzere iki asansör vardır. Murat ve Sadık aynı asansörde bulunmak koşuluyla 11 kişi asansörlere kaç farklı şekilde binebilir? A) 190 B) 200 210 D) 240 E) 280 25/605 84 12. koyo.

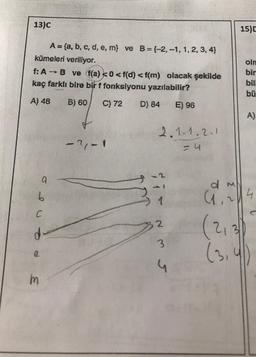
13)C A = (a, b, c, d, e, m) ve B=(-2,-1, 1, 2, 3, 4) kümeleri veriliyor. f: A - B ve f(a) <0 <f(d) <f(m) olacak şekilde kaç farklı bire bir f fonksiyonu yazılabilir? A) 48 B) 60 C) 72 D) 84 E) 96 2.1.1.2.1 -?/- 1 = 4 a b C d- m 1 2 35 G 15)D olm bir bil bü A) d (₁,~ 4 (2₁ (3₁4)

24. Anne, baba ve 3 çocuktan oluşan bir aile yatay sıra boyunca, çocukların üçü birden daima yan yana olmamak şartıyla kaç farklı şekilde ler? oturabilir- A) 72 B) 84 C) 92 D) 108 E) 112 AB 64G = 5! S! F 31. 2! 3! 120-72 48 Tüm D. 221 BENIM HOCAM BENİM BAŞARIM BENİM HOCAM BENİM BAŞARIM BENİM HOCAM BENİM BAŞARIM BENİM HOCAM BENİM BAS 26 27.

Barışın bir elinin 3 parmağında 2, 2 ve 1 adet olmak üzere toplam 5 yüzük vardır. e 178 Barış her seferinde sadece bir parmağından en üstteki bir yüzüğü çıkartmak şartıyla tüm yüzükleri parmaklarından çıkartacaktır. Buna göre, Barış bu işlemi kaç farklı şekilde ya- pabilir? A) 20 B) 28 C) 30 D) 35 E) 42

Testokul 22 19. 3 evli çift ile 2 bekârdan oluşan 8 kişilik arkadaş grubu bir kanepeye aşağıdaki koşullara uygun olarak oturacaktır. • Çiftlerin her biri eşleriyle yan yana oturacaktır. Bekârlar yan yana oturmayacaktır. Buna göre, bu kişiler kanepeye kaç farklı biçimde oturabilirler? A) 144 B) 288 C) 382 D) 576 E) 612

C) 8 D) 7 C+B 21A18+) 2B 2A+4B E) 6 A TOPPitone grup our. 25. 23. 80000 Bir bekleme salonunda bulunan (14 koltuğa 12 kişi rastgele oturuyor. A, B, C isimli belirli üç kişi yan yana olmak şartı ile kaç farklı şekilde oturulabilir? A) 25!.10 B) 11.24! C) 18.11 D) 12.10 E) 2.12! ABC -D 1 1 2 42 -3 1 O Şekilde y = f(x) fonksiyonunun grafiği

inasyon k at sunse met 2 Olasılık - II Bir çift zar atılıyor. Üst yüze gelen sayıların çar- pımının 20 den büyük olduğu bilindiğine göre bu zarlardan en az birinin 5 olma olasılığı kaçtır? A) 1/1 1. B) C) 1 D) E) 1/1/2 1/3 1 6 Hott vor 44

NRM DNM 211=2 MNB MBN 11. 7 rakamlı telefon numarasının ilk 4 rakamı ile son rakamı bilinmektedir. Kaç değişik deneme ile bu telefon numarası kesin olarak tespit edilebilir? 1A) 80 B) 90 C) 96 D) 98 E) 100 (2)-(2) Z.B.54 J 27 12. Beş katlı bir apartmanın her katı distan boya ESEN vardır? A) 10 TT 9/3 16.

Olasılık nde an a- Permütasyon 5. 2 çocuk, 2 erkek ve 2 kadın çocuklar bir arada olmamak koşuluyla yan yana kaç değişik biçimde oturabilir? A) 520 B) 480 C) 460 D) 440 E) 436 24 2€ 2ײ ~= 2!₁2!₁ \\ 2.2.2=8 8 26₁)₁ 2 = 2 ² = 51,12! 245/42,21 20 514.22111=240

DO! in son iki raka- sayı aşağıdaki- E) 40 TEST 4 Permütasyon - Kombinasyon Binom ve Olasılık 1. Bir arkadaş grubu, bir sıraya 120 değişik biçimde oturabilmektedir. Bu gruptaki herhangi 3 kişi yan yana duran 3 sandalyeye kaç farklı şekilde otura- bilir? A) 60 B) 48 C) 24 D) 18 E) 10 avtobnischer EX ninslivez legob Augimination cod Perr 5. 2 çocuk, 2 erkek ve 2 olmamak koşuluyla ya oturabilir? A) 520 B) 480 24 2€ 24 26

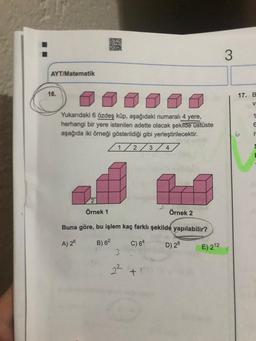
AYT/Matematik 16. Yukarıdaki 6 özdeş küp, aşağıdaki numaralı 4 yere, herhangi bir yere istenilen adette olacak şekilde üstüste aşağıda iki örneği gösterildiği gibi yerleştirilecektir. 1/2/3/4/ Örnek 1 Örnek 2 Buna göre, bu işlem kaç farklı şekilde yapılabilir? A) 26 B) 62 C) 64 D) 28 3 E) 212 3 17. B V 1 6 r

A) 90 B) 270 C) 810 D) 900 E) 1000 alto 1.V obsolu8 Solo2 bis bist ( a 0 A 03 9. A = {1, 2, 3, 4, a, b kümesinin elemanlarının her biri kul- lanılarak rakamlar soldan sağa artan sırada, harfler sağ- dan sola doğru alfabetik sırada olacak şekilde 12b3a4 şeklinde 6 haneli şifreler oluşturalacaktır. Buna göre, kaç farklı şifre oluşturulabilir? A) 15 B) 10 C) 20 D) 25 E) 30 13/2/11 6 26 fromları fark-

A) 212 B) 213 C) 214 D) 215 E) 216 32 un + 12. {4, 5, 6, 7, 8, 9) 62 ars kümesinin elemanlarıyla 3 ile tam bölünebilen 3 basamaklı rakamları farklı kaç farklı sayı yazıla- bilir? ling reğin A) 24 B) 32 C) 40 D) 48 E) 56