Permütasyon Soruları

2. Bir öğretmen, 5 öğrenciden yüzleri kendisine dönük olarak tek sıraya geçmelerini istiyor. Bu öğrencilerden ikisi aynı boydadır. Bu öğrencilerin öğretmene göre, soldan sağa ve kısa- dan uzuna doğru bir boy sırası oluşturma olasılığı kaçtır? 1 1 1 C) B) A) 30 60 120 E) D) 15

11. Aşağıda E harfinden baslayıp sondaki N harfine ka- dar komşu harfleri izleyerek EFLATUN kelimesi oku- nuyor. 6.7 A E F F L L L A A A T T T U U N Buna göre, şekilde kaç farklı EFLATUN kelimesi okunabilir? A) 35 B) 24 C) 20 D) 18 E) 10

örnek-12 1. satır → 2. satır A. 1. sütun 2. 3. sütun sütun 5. sütun sütun 1, 2, 3, 4, 5, 6, 7, 8, 9, 11 sayıları kullanılarak oluşturu- lan yukarıdaki tabloda her sütundaki sayıların toplamı çift sayıdır. Free Buna göre, bu sayılar tabloya kaç farklı şekilde yer- leştirilebilir? B) 5! - 46 C) 2.5!.6 D) 5.5! E) 10! A) 5!

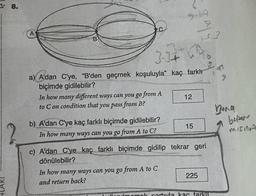
C A that B GO 3.14 h 9 a) A'dan C'ye, "B'den geçmek koşuluyla" kaç farklı biçimde gidilebilir? In how many different ways can you go from A 12 to Con condition that you pass from B? Bang beper 1 15 ? b) A'dan C'ye kaç farklı biçimde gidilebilir? In how many ways can you go from A to C? misinA c) A'dan C'ye kaç farklı biçimde gidilip tekrar geri dönülebilir? In how many ways can you go from A to C and return back? 225 NLARI mol cartila kar farkın

- erek birbi- örnek: Aşağıda 16 eş kareden oluşan şekil ve belirttikleri yollar çizil- miştir. A noktasından harekete başlayan bir hareketli sadece sağa veya yukarı doğru hareket ederek B noktasına gidecek tir. B D E A Buna göre, bu hareketli, a) A noktasından B noktasına kaç farklı yoldan gidebilir? tirilerek b) A noktasından B noktasına C noktasına uğramak şar- tryla kaç farklı yoldan gidebilir? ëls Yeyinion c) Dlle E noktaları arasındaki yol kapatılırsa, A noktasın- dan B noktasına kaç farklı yoldan gidebilir?

Temel Matematik 13 14 15 10 12 JOU - DOT 5 2 3 CE Bir sınıfta yukarıdaki gibi numaralanmış iki kişilik 15 sıra vardır. Bu siniftaki 20 kız ve 10 erkek öğrenci bu sıralara ikişerli olarak oturduğunda kız öğrencilerin hepsinin koridor tarafında oturma olasılığı kaçtır? 1 30! C) B) A) 1 20! 20! 30! D) 20! 10! 30! 1 (3.3 (3+2)(-2) 2 ( 2 or

E E VR NB E E 1 E S VR RMS N N E E 1 E E VR NB E En soldaki S harfinden başlayarak en sağdaki N harfine kadar komşu harfler takip edilerek SEVERİM SENİ BEN İfadesi kaç farklı şekilde okunabilir? A) 20 B) 40 C) 200 D) 360 E) 400

E) Cuma, cumartesi Curs Connor Port Pzt Sale Core Peso A B 26. 35.9 Hakan rakamları kullanarak 4 haneli bir şifreyi aşağıdaki koşullara göre oluşturacaktır. Şifrenin her hanesi asal sayıdır. Şifreye yazılan sayının kendisi ve tersten okunuşu ay- ni sayidir. Buna göre, Hakan şifresini kaç farklı şekilde oluşturu- labilir? A) 12 B) 16 C) 20 D) 24 E) 32 iki bin ve you elle sedi ye dibin ell yüz otuz il 4! = 4.3.2.1-25 41 Temel Matematik

D C 12. A B Kırmızı boya Beyaz boya Mavi boya Yeşil boya Pembe boya Şekilde verilen ABCD dikdörtgeni köşegenleri yardımıyla 4 eş bölgeye ayrılmıştır. Bu bölgeler yukarıda verilen kırmızı, beyaz, mavi, yeşil ve pembe renkli boyalardan biriyle boyanacaktır. Ortak kenara sahip olan bölgeler farklı renkle boyanmak şartıyla kaç değişik boyalı bölge deseni elde edilir? A 120 B) 200 C) 240 D) 260 E) 280 9.20 = 0

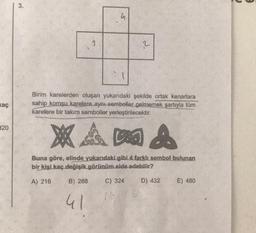
3 . a 2 kaç Birim karelerden oluşan yukarıdaki şekilde ortak kenarlara sahip komşu karelere aynı semboller gelmemek şartıyla tüm karelere bir takım semboller yerleştirilecektir. 320 XA DO A Buna göre, elinde yukarıdaki gibi 4 farklı sembol bulunan bir kişi kaç değişik görünüm elde edebilir? A) 216 B) 288 C) 324 D) 432 E) 480 41 75

28. 5 kişilik bir koşu takımı 5x100 m bayrak yarışı yapacaktır. Yarışa başlayan koşucu 100 m koştuktan sonra bayrağı ikinci koşucuya o da 100 m koştuktan sonra üçüncüye devamında da diğerleri bu şekilde 500 m'lik yarışı tamamlayacaktır. Bu koşuculardan ikisi olan Nevin ve Damla bayrağı birbirlerine vermek istediklerine göre, 5x100 m bayrak yarışı kaç farklı şekilde yapılabilir? A) 64 B) 48 C) 24 D) 32 E) 36

10. Aralarında Turan ile Seyit’in bulunduğu 9 kişinin 4'ü Ordu'ya, 5'i Çankırı'ya gönderilecektir. Turan'ın Ordu'ya, Seyit'in Çankırı'ya gideceği belli olduğuna göre bu gönderme işlemi kaç farklı şekilde yapılabilir? A) 21 B) 28 C) 35 D) 42 E) 56

36 03 EIM Luc ZA BD BD 5 6 2 3 Yukarıda 6 tane birim kareden oluşan CADDEM tabelasın- daki birim kareler 4 farklı renkteki boyalarla boyanacaktır. Yan yana bulunan iki tane birim kare farklı renge boya- nacaktır. 1 ve 6. bölümdeki birim kareler aynı renge boyanacak- Buna göre, bu tabela kaç farklı şekilde boyanabilir? A) 72 B) 144 C) 192 D) 216 E) 240 33

5. Anne, Baba ve 3 çocuktan oluşan 5 kişilik bir aile yan ya- na sıralanarak fotoğraf çektirecektir. Anne ile Baba'nın bir arada olduğu kaç farklı fotog. raf çektirirler? C) 48 D) 50 B) 46 A) 44 E) 52

E 2A + 304 = JA +44 2.2 J N 1675 in Aşağıda ikisi sarı, ikisi mavi, biri pembeye boyanmış birbirine eş 5 adet ahşap blok gösterilmiştir. izins ODE d. 19 2121 3.22 Şekil 1 Şekil 2 Ahşap blokların tamamını Şekil 2'de gösterildiği gibi üst üste sıralamak isteyen Melih, sıralamasını üst üste koyduğu herhangi iki ahşap blok birbirinden farklı renk- lerde olacak şekilde yapacaktır. Buna göre Melih, ahşap blokların tamamını bu ku- rala göre üst üste kaç farklı şekilde sıralayabilir? A), ch Dy 16 5/24 B) 10 C) 12 4+4+4th

15. 5 şişe gazozu olan Eda, gazozları günde en az bir şişe içerek art arda gelen günlerde bitirecektir. Örneğin, bir günde 3 şişe, diğer bir günde 2 şişe içebi- leceği gibi bir günde 2 şişe, diğer bir günde 2 şişe ve sonraki günde 1 şişe içerek de bitirebilecektir. Buna göre, Eda gazozların tümünü kaç değişik biçim- de içebilir? A) 21 B) 17 C) 16 D) 14 E) 10