Polinom Nedir, Polinom Formülleri ve Genel Bilgiler
n bir doğal sayı, a0, a1, a2, a3….a n gerçek sayılar olmak üzere
P(x)=a0+a1x+a2x2+a3x3+….+anxn
şeklindeki ifadelere gerçek katsayılı ve bir değişkenli polinom denir. Polinomun sözlük anlamı da “çok terimli” demektir.
- a0, a1, a2, a3….a n polinomun katsayılarıdır.
Kat sayılar toplamı için bir polinomda x yerine 1 konulur.
- a0, a1x, a2x2, a3x3….anxn polinomun terimleridir.
- x’in en büyük kuvveti olan doğal sayıya P(x) polinomunun derecesi denir.
- x’in en büyük kuvveti olan doğal sayıya P(x) polinomunun derecesi denir.
- a0 polinomun sabit sayısıdır.
Sabit terim için bir polinomda x yerine 0 konulur.
- “Aşağıdakilerden hangisi polinomdur/polinom değildir?” sorularında polinom tanımı dikkate alınmalıdır.
P(x)=2x2+3√x +4 (√x=x1/2 ve 1/2 doğal sayı değildir. Yani P(x) polinom değildir.)❌
Q(x)=3x3+3/x+7 (3/x=3x-1 -1 doğal sayı olmadığı için polinom değildir.) ❌
K(x)= x2-2x-5 (Üs doğal sayı, katsayı reel sayı yani ifade polinomdur.)✔
- x değişkeni bulundurmayan, c bir gerçek sayı olmak üzere P(x)=c polinomuna sabit polinom denir.
Örnek: P(x)=9, P(x)=163, P(x)=64…
- Sıfır polinomu sabit polinomun özel halidir. P(x)=0 polinomuna sıfır polinomu denir.
- Sabit polinom derecesi sıfır olan polinomdur.
- Sıfır polinomunun derecesi belirsizdir.
- Tek dereceli terimlerin katsayılar toplamı aşağıdaki formülle bulunur:
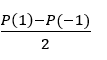
P(1) yazdığımız zaman hem tek hem çift dereceli terimlerin katsayıları toplamını buluruz. P(-1) yazdığımız zaman ise çift dereceli terimlerin katsayılarını ve tek dereceli terimlerin eksi ile çarpılmış katsayıları toplamı bulunur. Bu nedenle P(1)-P(-1) yaptığımız zaman tek dereceli terimlerin katsayılarını iki kez toplamış oluyoruz. İşlemin sonunda bu farkı ikiye bölerek tek dereceli terimlerin katsayıları toplamına ulaşırız. İlk başta formül gibi görünse de nereden geldiğini anladığımız zaman kolaylıkla bulabileceğimiz bir işlemdir.
- Çift dereceli terimlerin katsayıları toplamı aşağıdaki formülle bulunur:
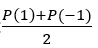
Bu işlemi de eğer unutursan yukarıda yaptığımız gibi düşünerek kolaylıkla çıkarabilirsin.
☀️
Konu anlatımları, sınav tavsiyeleri, rehberlik ve motivasyon içerikleri, güncel duyurular… Kunduz Blog, sınava dair ihtiyacın olan tüm içerikleri sana sunuyor. Şimdi buraya tıklayarak e-mail bültenimize ücretsiz abone ol, hiçbir içeriğimizi kaçırma!
☀️
Polinom Dereceleri ile İlgili İşlemler
Polinomlar konusunda çalışmazsan zorlanabileceğin bir başlığa geldik. Polinomlarda işlem yaparken zorlanırsan Üslü Sayılar yazımı okumanı öneririm. Çünkü polinomlarda işlem yaparken üslü sayılar bilgilerimizi kullanıyoruz.
der[P(x)]=m, der[Q(x)]=n, m, n ve a, b, k birer gerçek sayı olmak üzere,
- der[P(ax+b)]=m
- der[P(x).Q(x)]=m+n
- der[P(x)]k=m.k
- der[P(x)+Q(x)]=m der[P(x)-Q(x)]=m
- der[P k(x)]=m.k
P(x) polinomunun (x-a) bölümünden kalan:
P(x) polinomunda x-a bölümünden elde edilen kalan, P(x) polinomunda x yerine a yazılarak bulunan P(a) değeridir.
NOT: Polinomlarda bölme işlemi yapmadan kalanı bulmak için böleni sıfır yapan kökü polinomda yerine yazmalıyız.
P(x) polinomunun (ax2+bx+c) bölümünden kalan:
Genellikle sorularda hesaplamanın kolay olması için böleni çarpanlarına ayrılabilecek bir ifade verecektir. Böleni çarpanlarına ayırdıktan sonra yine x-a’daki gibi sıfıra eşitleyerek x yerine yazılır ve kalan olacak ax+b ye eşitlenir. İkinci dereceden bir ifadeye böldüğümüz için kalan birinci dereceden olabilir bu nedenle kalanı ax+b olarak alabiliriz.
Konu anlatımları, sınav tavsiyeleri, rehberlik ve motivasyon içerikleri, güncel duyurular… Kunduz Blog, sınava dair ihtiyacın olan tüm içerikleri sana sunuyor. Şimdi buraya tıklayarak e-mail bültenimize ücretsiz abone ol, hiçbir içeriğimizi kaçırma!
Bilgileri, tanımları ve önemli tarihi gelişmeleri öğrendikten sonra, soruların içinde nasıl yer aldığını görmen gerekli. Matematik Konu anlatımı yazımıza da göz attıktan sonra, kendi kaynaklarından sonra MEB Kaynaklarına da göz atmanı tavsiye ediyoruz.
☀️☀️☀️
Her ders için değişmeyen kilit nokta bol bol soru çözümü ile pratik yapmak. Çözemediğin sorulara yanıt bulmak istiyorsan sınava hazırlık sürecinde Kunduz hep yanında! Profesyonel eğitmenler tarafından hazırlanan Soru Çözümü, binlerce soru ve çözümden oluşan Soru Bankası hizmetlerinden faydalanabilirsin.

