Permutations and Combinations Questions and Answers

Math
Permutations and CombinationsA lottery system uses six digits The possible entries in these digits are the numbers 1 2 3 4 or letters n m o q s w and z The numbers or letters drawn can be repeated What is the total number of lottery sequences that can be made 823 543 1 771 561 1 000 000 121 745

Math
Permutations and CombinationsSuppose 13 people qualify for a college cheerleading squad five women and eight men How many six member squads can be selected if exactly two of the members are male Select one O a 715 b 140 OG 1417 d 33

Math
Permutations and CombinationsShelby does a probability experiment She spins this spinner and then filps a coin Green Yellow Purple Red Which list shows all the possible outcomes OA Green Heads Blue Heads Purple Heads Red Heads Yellow Heads OB Green Heads Blue Heads Purple Heads Red Heads Green Tails Blue Talls Purple Talls Red Talls OC Green Talls Blue Talls Purple Talls Red Talls Yellow Tails OD Green Head Blue Heads Purple Heac Red Heads Yellow Head Green Talls Blue Tails Purple Talls Red Talls Yellow Tails

Math
Permutations and CombinationsThe owner of Brookstone coffee has 13 regular full time employees 7 are female and 6 are male As he plans the schedule he likes to ensure exactly two employees on any given shift are male If 5 work a shift how many combinations can be created

Math
Permutations and CombinationsFor her show Outfront Alicia can air 2 segments If she has 14 segments to select from in how many ways can she arrange the segments for her show 91 X

Math
Permutations and CombinationsMs Bell s mathematics class consists of 13 sophomores 6 juniors and 11 seniors How many different ways can Ms Bell create a 5 member committee of seniors if each senior has an equal chance of being selected

Math
Permutations and CombinationsB Guests at a wedding have an appetizer choice of soup or a salad an entr e choice of chicken steak or vegetarian then a dessert choice of vanilla or chocolate cake How many different meals are possible

Math
Permutations and CombinationsThere are 30 students in a high school senior class. In how many ways could the yearbook choose the winners of Most Athletic, Class Clown, and Best School Spirit?

Math
Permutations and CombinationsCustomer account "numbers" for a certain company consists of 4 letters followed by 3 single-digit numbers. How many different account numbers are possible if repetitions of letters and digits are allowed?

Math
Permutations and CombinationsIn a high school basketball team there are 12 students competing to start a game. If 5 students can be chosen to start a game, how many different starting lineups can be formed from this group of 12 students?
3,991,680
95,040
120
792

Math
Permutations and CombinationsPlease show all the work that you go through in order to complete the problems.
1. As part of an exercise in an elementary school reading class, the students are given 6 cards that each contain a picture and part of a story. The students are asked to put the cards into an order that tells a coherent story. If a student didn't understand the assignment and had no idea what the intended order was, how many different possible ways could that student choose to place the cards down in order?

Math
Permutations and CombinationsFor a certain website, your password must be 10 digits long. If the first 8 digits are any numbers and the last 2 digits are any lower case letters, how many passwords are possible?
67,600,000,000
5,200,000,000
67,600
4,160

Math
Permutations and CombinationsThere were 24 students running in a race. How many different arrangements of first, second, and third place are possible?

Math
Permutations and CombinationsHow many different license plates can the State of lowa produce if the requirements are as
follows: 5 slots The first two slots are for letters. The next three slots are for digits from 0 - 9.
1, 240,000
676,000
82
1,757, 600

Math
Permutations and CombinationsA combination for a keypad is 6 digits long. The digits are from 0-9. The same digits MAY
NOT be used more than once. How many different combinations are there?
54
1,000,000
60
151, 200

Math
Permutations and CombinationsA lock has a 3-number code made up of 20 numbers. If none of the numbers are allowed to repeat, how many different ways can you choose three different numbers in order for a unique code?

Math
Permutations and CombinationsLorena has a bag containing 5 marbles of different colors to use for a statistics experiment. She asks a person to pull out 2 marbles, one at a time, without replacing them. Then she tallies the colors chosen. How many pairs of colored marbles are there?

Math
Permutations and Combinations(6 points) This test contains a total of 7 multiple choice questions, and each multiple choice question features 5 possible answers. (Someone guessing all "a's." for example, would have a string of multiple choice answers that reads "aaaaaaa.") How many strings of multiple choice answers are there that have "e" as the first choice?
(b) 6
(c) 6
(d) 57-1
(e) 5

Math
Permutations and CombinationsIn 2010, the state of Nevada had two area codes. The first three are the area code and the next seven are the local telephone number. (Note that at this time, a local telephone number cannot begin with 0 or 1) How many telephone numbers could Nevada's phone system have accomodated?

Math
Permutations and CombinationsIn Pennsylvania, each standard automobile license plate number consists of three letters followed by a four-digit number. How many distinct Pennsylvania license plate numbers can be formed?

Math
Permutations and CombinationsHow many three digit numbers can be
formed under each condition?
a) The leading digit cannot be 0.
b) The leading digit cannot be 0 and no
repetition of digits is allowed.
c) The leading digit cannot be 0 and the
number must be a multiple of 5.


Math
Permutations and CombinationsA college student is preparing a course schedule for the next semester. The student must select one of two mathematics courses, one of three science courses, and one of five courses from the social science and humanities. How many schedule are possible?


Math
Permutations and CombinationsHow many code symbols can be formed using 3 out of 7 letters of A, B, C, D, E, F, G if the letters:
a) are not repeated?
b) can be repeated?
c) are not repeated but must begin with D?
d) are not repeated but must begin with DE?
For each part, give the answer using permutation notation, factorial notation, or other operations. Then evaluate.
E. 1.6P2
G. 75
F. 6!
H. 7³
There are 30 possible code symbols.
(Simplify your answer.)
d) What is the answer using the proper notation?
A. 77
C. 5!
E. 1.6P2
G. 75
B. 6!
D. 7!
F. 7³
H.1.1.5P1
There are 5 possible code symbols.
(Simplify your answer.)

Math
Permutations and CombinationsTwelve students entered an essay contest in which the winner gets $500, second place gets $200, and third place gets $100. How many ways are there to rank the students first, second, and third? Each student only entered one essay and no student received two prizes.
1,320
220
33
132

Math
Permutations and Combinations(ii) How many groups of nine can be chosen that contain at least one man?
As in Example 9.5.7b, consider the relationship between the set of groups that consist entirely of women and the set of groups with at least one man. This thinking leads to the
conclusion that the number of groups with at least on man is
(iii) How many groups of nine can be chosen that contain at most three women?
A group of nine that contains at most three women can contain no women, one woman, two women, or three women. So, the number of groups of nine that contain at most three women is

Math
Permutations and CombinationsExplain how you know when a scenario describes a permutation situation versus a combination situation.
Give an example of a permutation scenario not mentioned in this lesson.

Math
Permutations and CombinationsA poll is given, showing 55% are in favor of a new building project. If 8 people are chosen at random, what is the probability that exactly 5 of them favor the new building project?

Math
Permutations and CombinationsPadlocks with digit dials are often referred to as "combination locks" According to the mathematical definition of combination, is this an accurate description? Explain.
A combination is a subset of objects or choices in which the order
A permutation is a subset of objects or choices in which the order
Therefore, the description of Combination Locks mathematically accurate.

Math
Permutations and CombinationsA license plate is to consist of 2 letters followed by 3 digits. Determine the number of different license plates possible if repetition of letters and numbers is permitted.
650,000
468,000
676,000
6,760,000

Math
Permutations and CombinationsA bag contains 5 red and 5 white tokens. Tokens are randomly selected and removed one at a time until the bag is empty. Find the probability that the red tokens are drawn consecutively.
In how many different ways can the tokens be drawn? ___
The probability that the red tokens are drawn consecutively is ___


Math
Permutations and CombinationsHow many ways can five people can be seated around a circular table if Dave is always immediately to the right of Pete?

Math
Permutations and CombinationsThe combination to a lock consists of a sequence of three numbers in the range 0-42.
a) How many combinations are possible in which no two consecutive numbers can be the same?
b) How many combinations are possible in which all three numbers are different?
c) What is the probability that the combination of a randomly-chosen lock consists of three different numbers?
d) What is the probability that the combination of a randomly-chosen lock contains at least one repeated number?
a) If no two consecutive numbers can be the same, write the expression (consisting of a product of numbers) that represents the number of possible combinations. ___
(Do not simplify.)
Thus, if no two consecutive numbers can be the same, the number of combinations is ___
(Simplify your answer.)
b) If all three numbers are different, the number of combinations is ___
(Simplify your answer.)
c) The probability that the combination of a randomly-chosen lock consists of three different numbers is. ___
(Round to two decimal places as needed.)
d) The probability that the combination of a randomly-chosen lock contains a repeated number is ___
(Round to two decimal places as needed.)

Math
Permutations and Combinationsa) How many plates are possible when letters and numbers can repeat? Set up the expression that can be used to calculate the number of plates that are possible when letters and numbers can repeat.
The expression is. ___ (Do not simplify.)
The number of plates possible when letters and numbers can repeat is. ___
(Use scientific notation. Use the multiplication symbol in the math palette as needed. Round to three decimal places as needed.)
b) How many plates would be possible if letters could repeat but numbers could not? ___
(Use scientific notation. Use the multiplication symbol in the math palette as needed. Round to three decimal places as needed.).
c) How many plates would be possible if letters could not repeat but numbers could? ___
(Use scientific notation. Use the multiplication symbol in the math palette as needed. Round to three decimal places as needed.)
d) How many plates would be possible if neither letters nor numbers could repeat? ___
(Use scientific notation. Use the multiplication symbol in the math palette as needed. Round to three decimal places as needed.)
e) What is the probability that a randomly generated plate has no repeating letters or numbers? ___
(Type an integer or decimal rounded to three decimal places as needed.)

Math
Permutations and CombinationsRadio stations in a certain country use a sequence of 4 or 5 letters as their station identification call letters. The first letter must be W, P, A, or Q. Assume there are no restrictions on the remaining letters, and repetition is allowed.
a) How many 4-letter station identifications are possible?
b) How many 5-letter station identifications are possible?
c) How many total station identifications are possible?
d) The identification for a randomly-chosen radio station is 4 letters in length. What is the probability that all four letters are different?
a) Set up the expression that would be used to calculate the number of possible 4-letter station identifications.
The expression is ___
(Do not simplify.)
There are ___ possible 4-letter station identifications.
(Simplify your answer.)
b) There are ___ possible 5-letter station identifications.
(Simplify your answer.)
c) The total number of possible station identifications is ___
(Simplify your answer.)
d) If the identification for a randomly-chosen radio station is 4 letters in length, then the probability that all four letters are different is ___
(Round to three decimal places as needed.)

Math
Permutations and CombinationsGlenn and Kim are members of a comedy troupe that has 11 members in all. How many ways can the 11 members line up if Glenn and Kim must stand side by side?
Give the expression that can be used to calculate the number of ways the members of the troupe can line up. Choose the correct answer below.
O A.11!*2
O B.9!*10
O C.9!*2
O D.9!
O E.11!*10
O F.11!*10*2
O G.9!*10*2
O H.11!
The number of ways that the troupe can line up is.
(Simplify your answer.)

Math
Permutations and CombinationsA man has 4 shirts and 3 ties. How many different shirt and tie arrangements can he wear?

Math
Permutations and CombinationsAn automobile designer is considering three body designs, five hood designs, and three fender designs. How many models would be required to show all possible ways of combining the designs?
45
42
11

Math
Permutations and CombinationsCONSTRUCTING A TEST- A TEACHER IS CONSTRUCTING A MATHEMATICS TEST
CONSISTING OF 10 QUESTIONS. SHE HAS A POOL OF 28 QUESTIONS, WHICH ARE
CLASSIFIED BY LEVEL OF DIFFICULTY AS FOLLOWS: 6 DIFFICULT QUESTIONS, 10
AVERAGE QUESTIONS, AND 12 EASY QUESTIONS. HOW MANY DIFFERENT 10
QUESTION TESTS CAN SHE CONSTRUCT FROM THE POOL OF 28 QUESTIONS IF
HER TEST IS TO HAVE 3 DIFFICULT, 4 AVERAGE, AND 3 EASY QUESTIONS?
Math
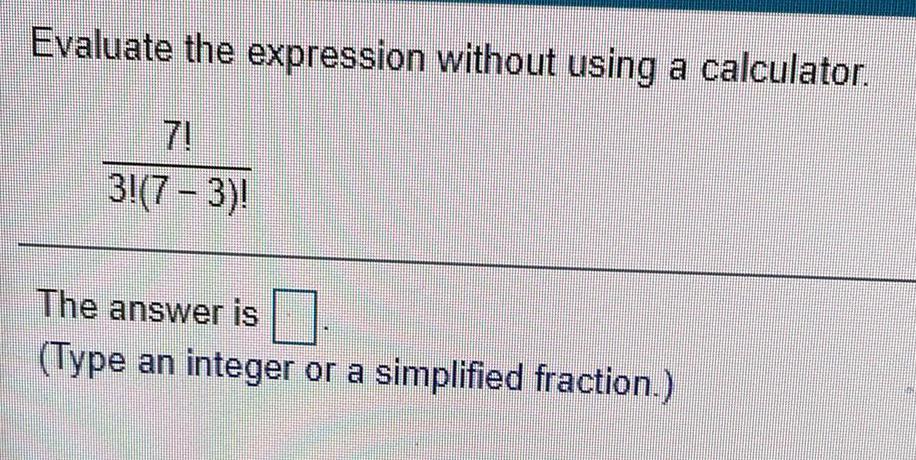
Permutations and CombinationsEvaluate the expression without using a calculator.
7!/3!(7-3)!
The answer is __
(Type an integer or a simplified fraction.)

Math
Permutations and CombinationsSuppose there is a list of fifteen jokes about marriage and divorce. In how many ways can people select their five favorite jokes from this list?
Five favorite jokes can be selected from a list of fifteen thoughts about marriage and divorce in different ways.
(Type a whole number.)

Math
Permutations and CombinationsDirections Answer the questions. All problems are with replacement.
1. How many 3-digit area codes can be made with the digits 0 through 9?
2. If area codes were changed from 3-digit to 4-digit numbers, how many more area codes would be made available?
3. How many 5-character PIN numbers can be made that contain 2 letters followed by 3 digits?
4. In a certain city, all phone numbers begin with one of 5 different 3-digit exchanges. How many different telephone numbers are possible for this area?
5. In the city in problem 4, how many new 3-digit exchanges would need to be added to allow for a total of 120,000 phone numbers?

Math
Permutations and CombinationsThis test contains a total of 7 multiple choice questions, and each multiple choice question features 5 possible answers. (Someone guessing all "a's." for example, would have a string of multiple choice answers that reads "aaaaaaa.") How many total strings of multiple choice answers are possible for our test?
(a) 7⁵
(b) 5!
(c) (7/5)
(d) 5⁷
(e) 1+2⁷ +3⁷ +4⁷ +5⁷
Math
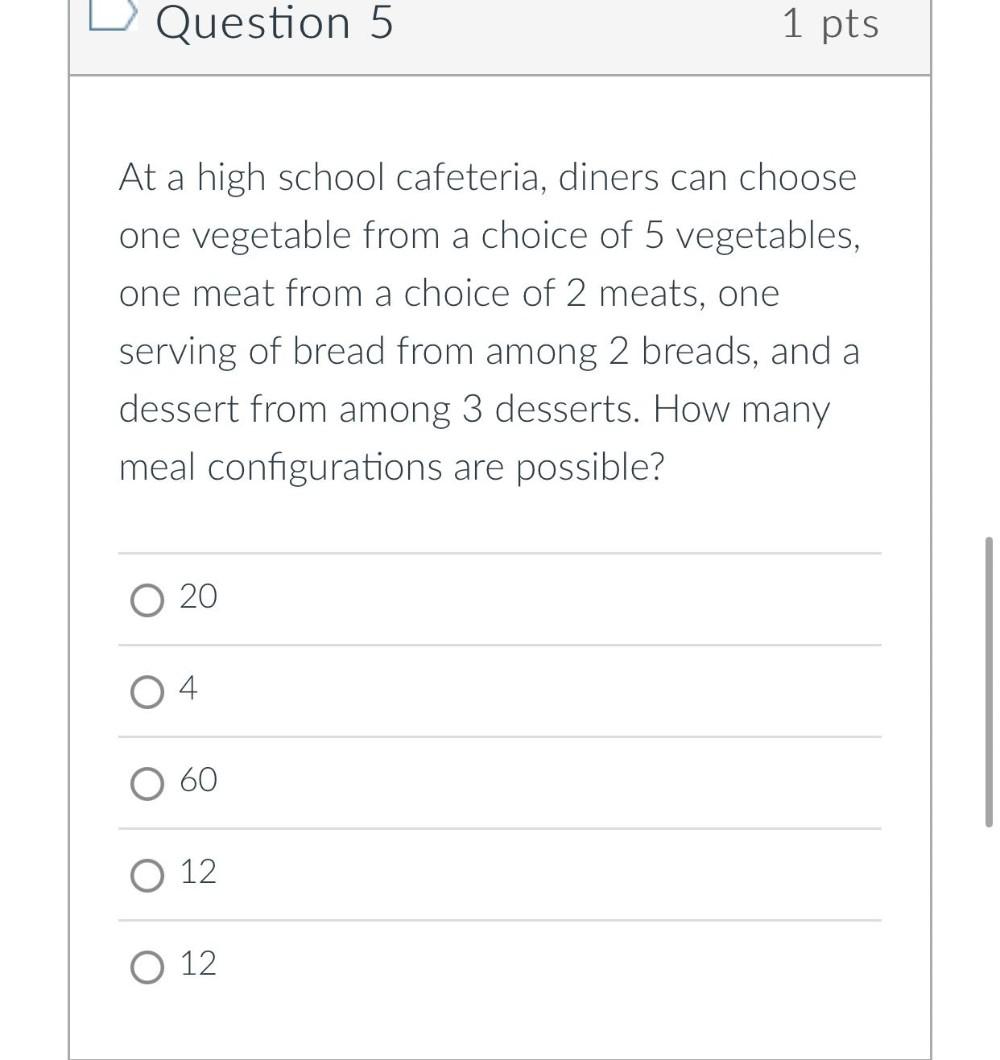
Permutations and CombinationsAt a high school cafeteria, diners can choose one vegetable from a choice of 5 vegetables, one meat from a choice of 2 meats, one serving of bread from among 2 breads, and a dessert from among 3 desserts. How many meal configurations are possible?
a) 20
b)4
c)60
d)12
d)12
Math
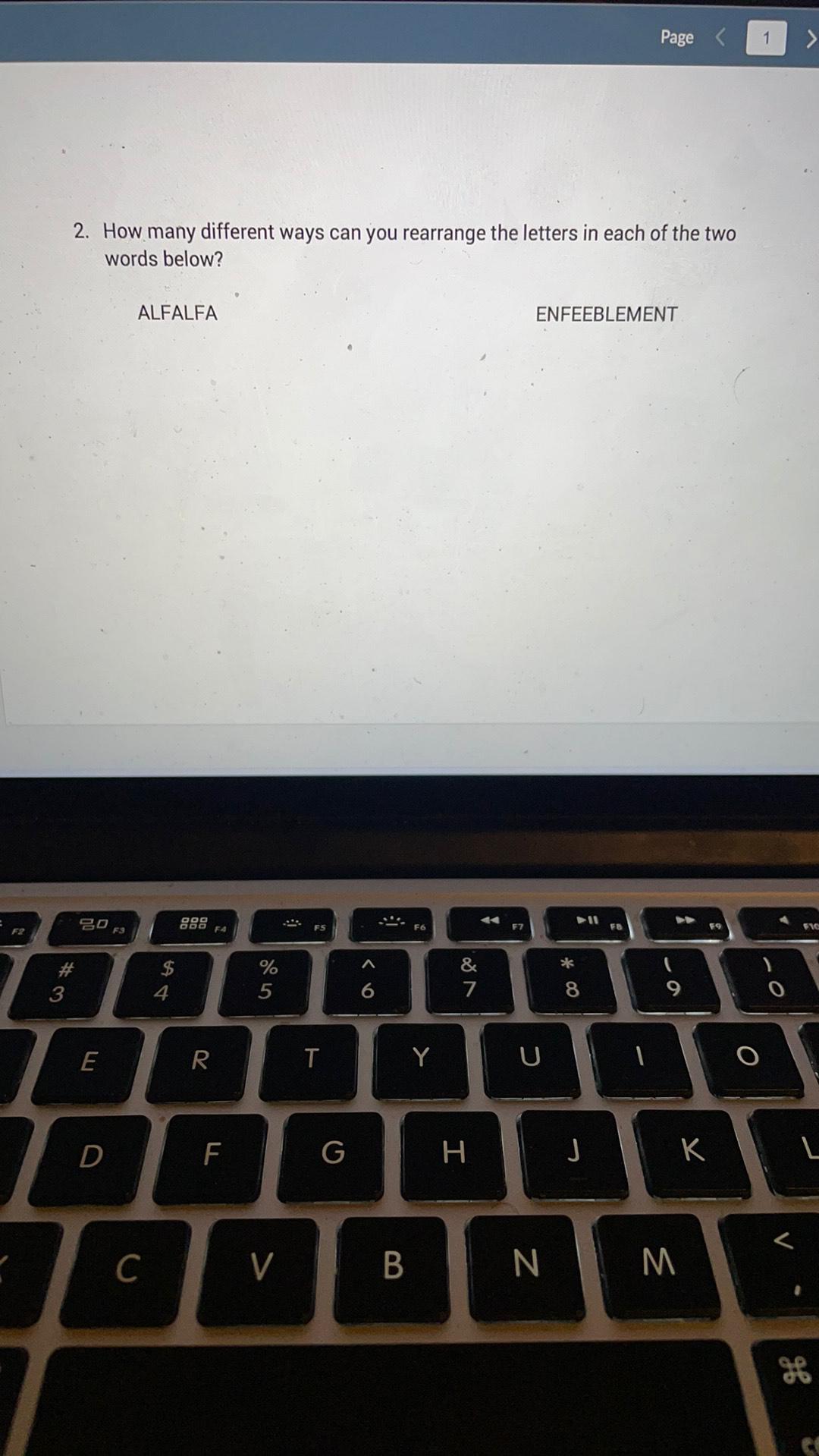
Permutations and CombinationsHow many different ways can you rearrange the letters in each of the two
words below?
ALFALFA ENFEEBLEMENT
Math
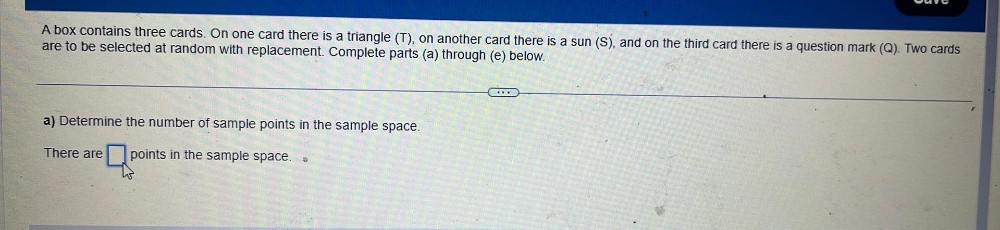
Permutations and CombinationsA box contains three cards. On one card there is a triangle (T), on another card there is a sun (S), and on the third card there is a question mark (Q). Two cards are to be selected at random with replacement. Complete parts (a) through (e) below.
a) Determine the number of sample points in the sample space.

Math
Permutations and CombinationsWhich conditions are needed to conduct a one-proportion z test? (Check all that apply)
1. The probability of each sample is within 1 standard deviation of the mean
2. The samples are approximately normally distributed
3. The population proportion is statistically significant.
4. Each sample is independent of the others.
5. The sample was collected randomly.

Math
Permutations and CombinationsMs. Bell's mathematics class consists of 13 sophomores, 6 juniors, and 11 seniors. How many different ways can Ms. Bell create a 5-member committee of seniors if each senior has an equal chance of being selected?