Determine whether the following statements are true and give

Last updated: 1/23/2024

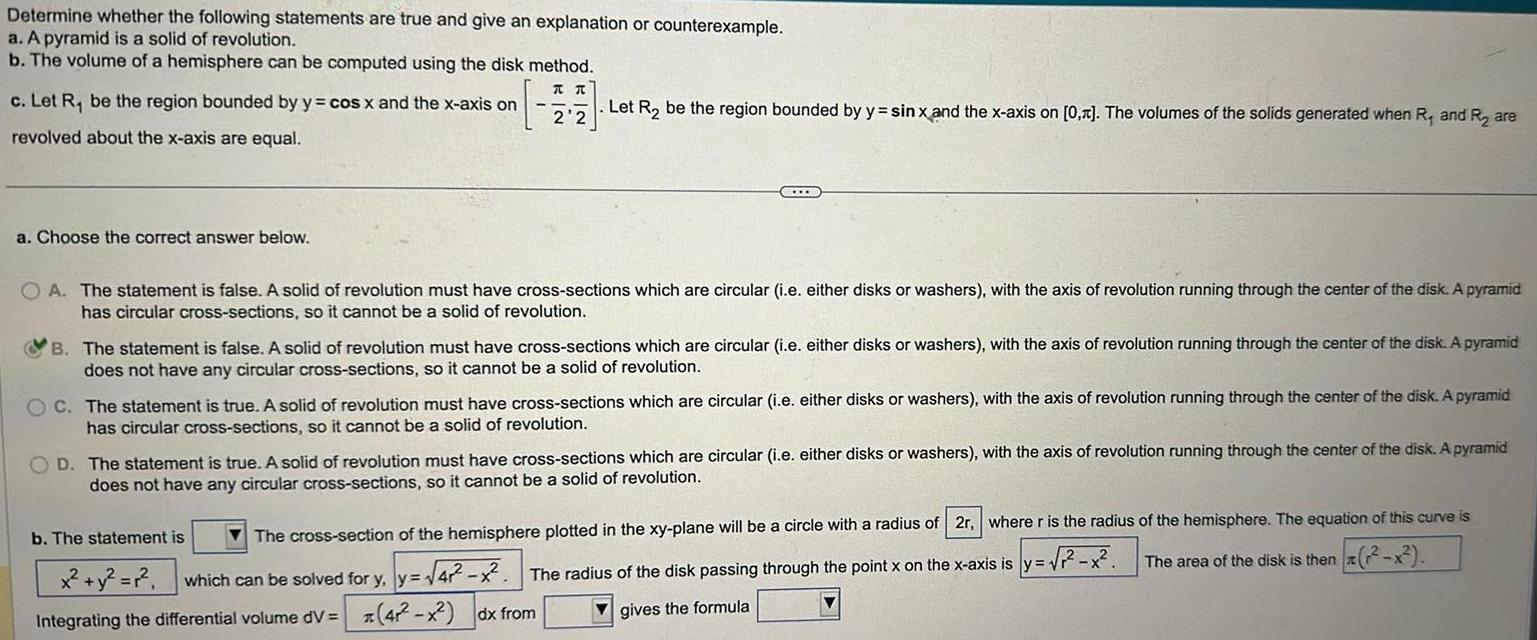
Determine whether the following statements are true and give an explanation or counterexample a A pyramid is a solid of revolution b The volume of a hemisphere can be computed using the disk method TR 2 2 Let R be the region bounded by y sin x and the x axis on 0 The volumes of the solids generated when R and R are c Let R be the region bounded by y cos x and the x axis on revolved about the x axis are equal a Choose the correct answer below C OA The statement is false A solid of revolution must have cross sections which are circular i e either disks or washers with the axis of revolution running through the center of the disk A pyramid has circular cross sections so it cannot be a solid of revolution B The statement is false A solid of revolution must have cross sections which are circular i e either disks or washers with the axis of revolution running through the center of the disk A pyramid does not have any circular cross sections so it cannot be a solid of revolution OC The statement is true A solid of revolution must have cross sections which are circular i e either disks or washers with the axis of revolution running through the center of the disk A pyramid has circular cross sections so it cannot be a solid of revolution D The statement s true A solid of revolution must have cross sections which are circular i e either disks or washers with the axis of revolution running through the center of the disk A pyramid does not have any circular cross sections so it cannot be a solid of revolution The cross section of the hemisphere plotted in the xy plane will be a circle with a radius of 2r where r is the radius of the hemisphere The equation of this curve is The area of the disk is then z x b The statement is x y r which can be solved for y y 4 The radius of the disk passing through the point x on the x axis is y x Integrating the differential volume dV 4 x dx from gives the formula