et 7 R4 R3 be the linear transformation represented by T x
Last updated: 4/2/2024
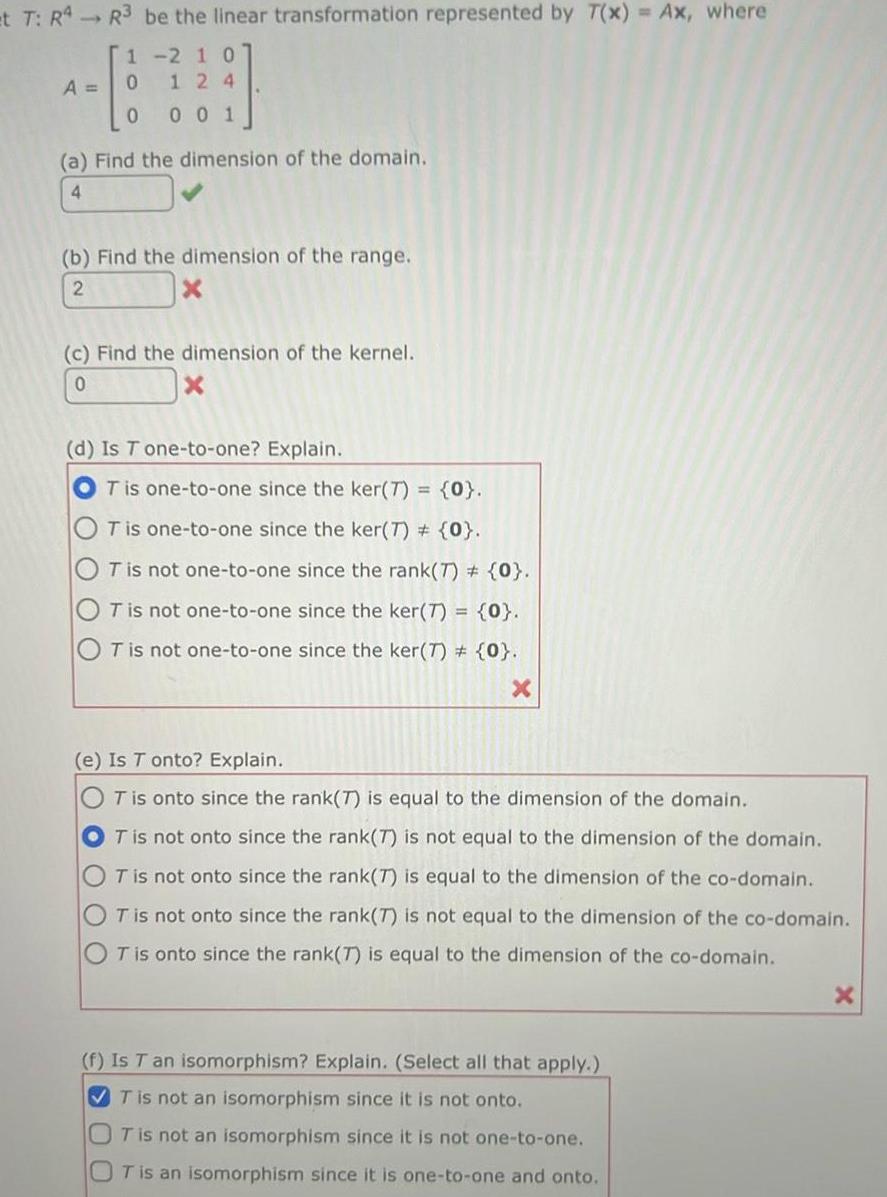
et 7 R4 R3 be the linear transformation represented by T x Ax where A 1 210 100 124 001 a Find the dimension of the domain 4 b Find the dimension of the range 2 X c Find the dimension of the kernel 0 X d Is T one to one Explain T is one to one since the ker 7 0 T is one to one since the ker 7 0 T is not one to one since the rank 7 0 T is not one to one since the ker 7 0 T is not one to one since the ker 7 0 e Is T onto Explain T is onto since the rank 7 is equal to the dimension of the domain OT is not onto since the rank 7 is not equal to the dimension of the domain T is not onto since the rank 7 is equal to the dimension of the co domain T is not onto since the rank 7 is not equal to the dimension of the co domain T is onto since the rank 7 is equal to the dimension of the co domain f Is T an isomorphism Explain Select all that apply T is not an isomorphism since it is not onto T is not an isomorphism since it is not one to one OT is an isomorphism since it is one to one and onto X