Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
Calculus
Limits & Continuity1 lim 2x 6 Hint Use the inequality a b a bl M x 3 which holds for all constants a and b see Exercise 74


Calculus
Vector Calculus3 Finding for a given e using a graph Let f x x 3 and note that lim f x 3 For each value of e use a graphing utility x 0 to find all values of 8 0 such that f x 3 whenever 0 x 0 8 Sketch graphs illustrating your work a 1 b e 0 5
Calculus
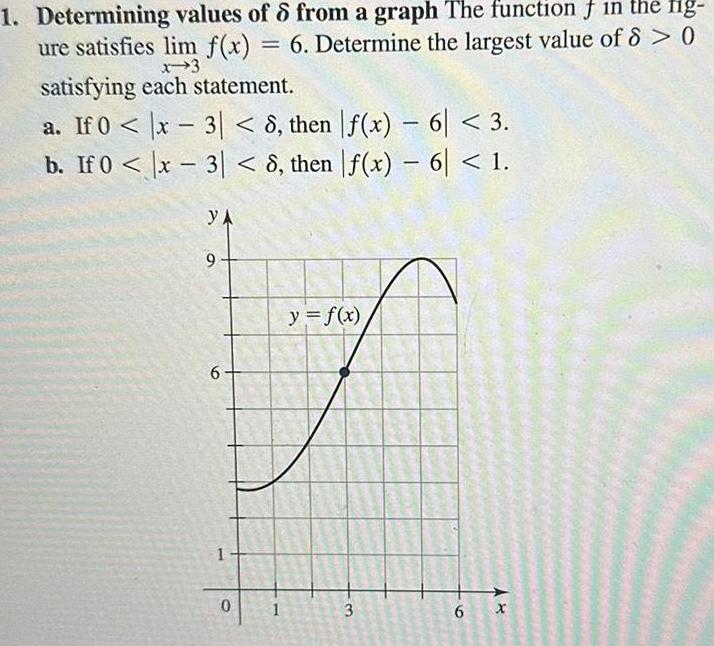
Application of derivatives1 Determining values of 6 from a graph The function in the fig ure satisfies lim f x 6 Determine the largest value of 8 0 x 3 satisfying each statement a If 0 x 3 8 then f x 6 3 b If 0 x 3 8 then f x 6 1 YA 9 6 1 0 1 y f x 3 REGA 6 x

Calculus
DifferentiationSuppose f z is continuous on 4 7 and 4 f x 4 for all az in 4 7 Use the Mean Value Theorem to estimate f 7 f 4 Answer f 7 4
Calculus
Differential equationsConsider the function f 1 1 4z 6 on the interval 0 4 Verify that this function satisfies the three hypotheses of Rolle s Theorem on the inverval f x is on 0 4 f z is on 0 4 and f 0 f 4 Then by Rolle s theorem there exists at least one value e such that f c 0 Find all such values c and enter them as a comma separated list Values of c
Calculus
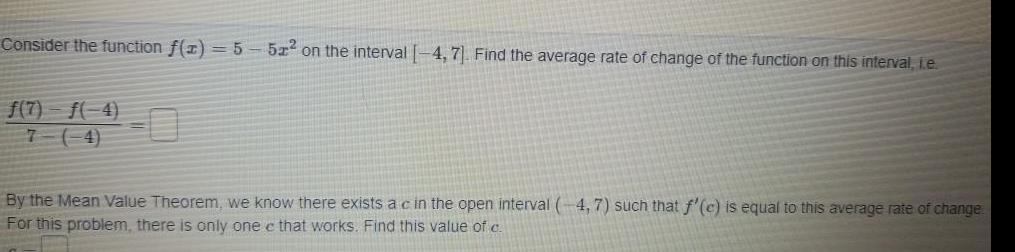
Application of derivativesConsider the function f x 5 f 7 f 4 7 4 51 on the interval 4 7 Find the average rate of change of the function on this interval i e By the Mean Value Theorem we know there exists a c in the open interval 4 7 such that f c is equal to this average rate of change For this problem there is only one e that works Find this value of c
Calculus
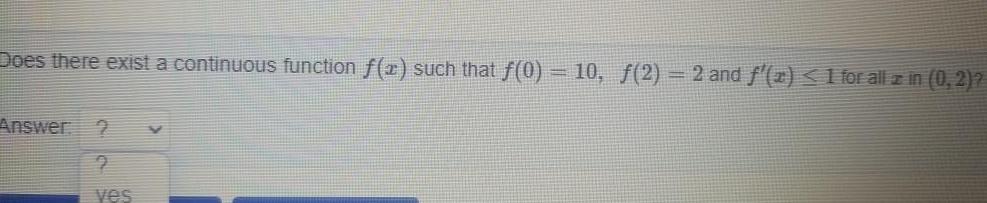
Indefinite IntegrationDoes there exist a continuous function f x such that f 0 10 2 2 and f x 1 for all z in 0 2 Answer 2 9 ves

Calculus
Application of derivativesa Evaluate the integral 32 S x 4 Your answer should be in the form k where k is an integer What is the value of k darctan a Hint dz dx a1 a2 a3 1 224 1 k 4 b Now lets evaluate the same integral using power series First find the power series for the function f x 324 Then integrate it from 0 to 2 and call it S S should be an infinite series 4 What are the first few terms of S ao a4 c The answers to part a and b are equal why Hence if you divide your infinite series from b by k the answer to a you have found an estimate for the value of 7 in terms of an infinite series Approximate the value of TT by the first 5 terms d What is the upper bound for your error of your estimate for if you use the first 7 terms Use the alternating series estimation

Calculus
Application of derivativesover each of the indicated intervals a Interval 10 0 1 Absolute maximum 2 Absolute minimum b Interval 7 2 1 Absolute maximum 2 Absolute minimum c Interval 10 2 1 Absolute maximum 2 Absolute minimum f x x 12x 27x 6
Calculus
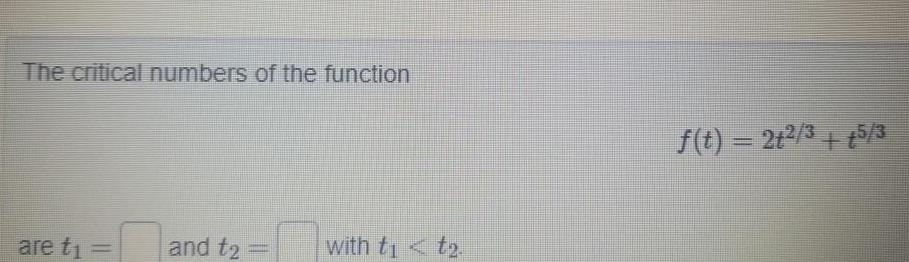
Application of derivativesThe critical numbers of the function are t and t2 with tit f t 2t 3 5 3
Calculus
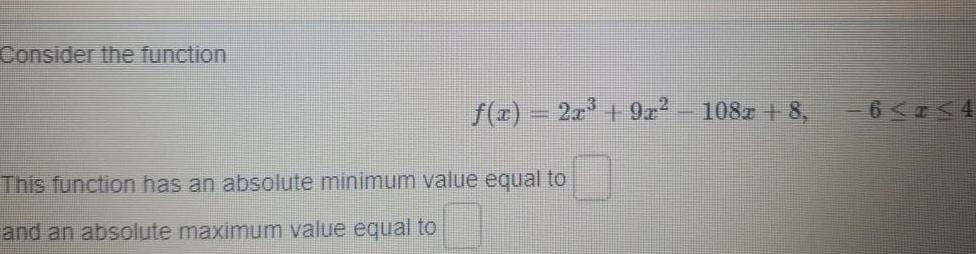
Vector CalculusConsider the function f x 2x 9x This function has an absolute minimum value equal to and an absolute maximum value equal to 108 8 6 7 4

Calculus
Differential equationsFind all angles between 0 and 180 satisfying the given equation Round your answer to one decimal place Enter your answers as a comma separated list Enter your answer in degrees sin 0 0 51 05 9

Calculus
Application of derivativesme function f x 7 4 e 21 has one critical number Find the critical number

Calculus
DifferentiationUse a calculator to find an approximate value in radians of the expression rounded to five decimal places if it is defined If a answer is undefined enter UNDEFINED 8 cos 8 X

Calculus
Differentiation0 1 Points 8 DETAILS sin PREVIOUS ANSWERS MY NOTES Find all angles between 0 and 180 satisfying the given equation Round your answer to one decimal place Enter your answers as a comma separated list Enter degrees P

Calculus
Definite IntegralsThe sun is 22 above the horizon Find the length of a shadow cast by a park statue that is 12 feet tall Round your answer to one decimal place ft
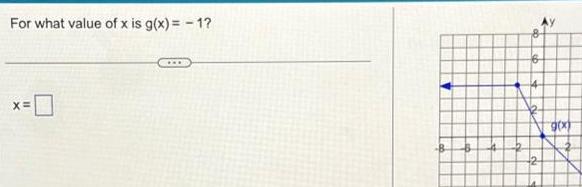
Calculus
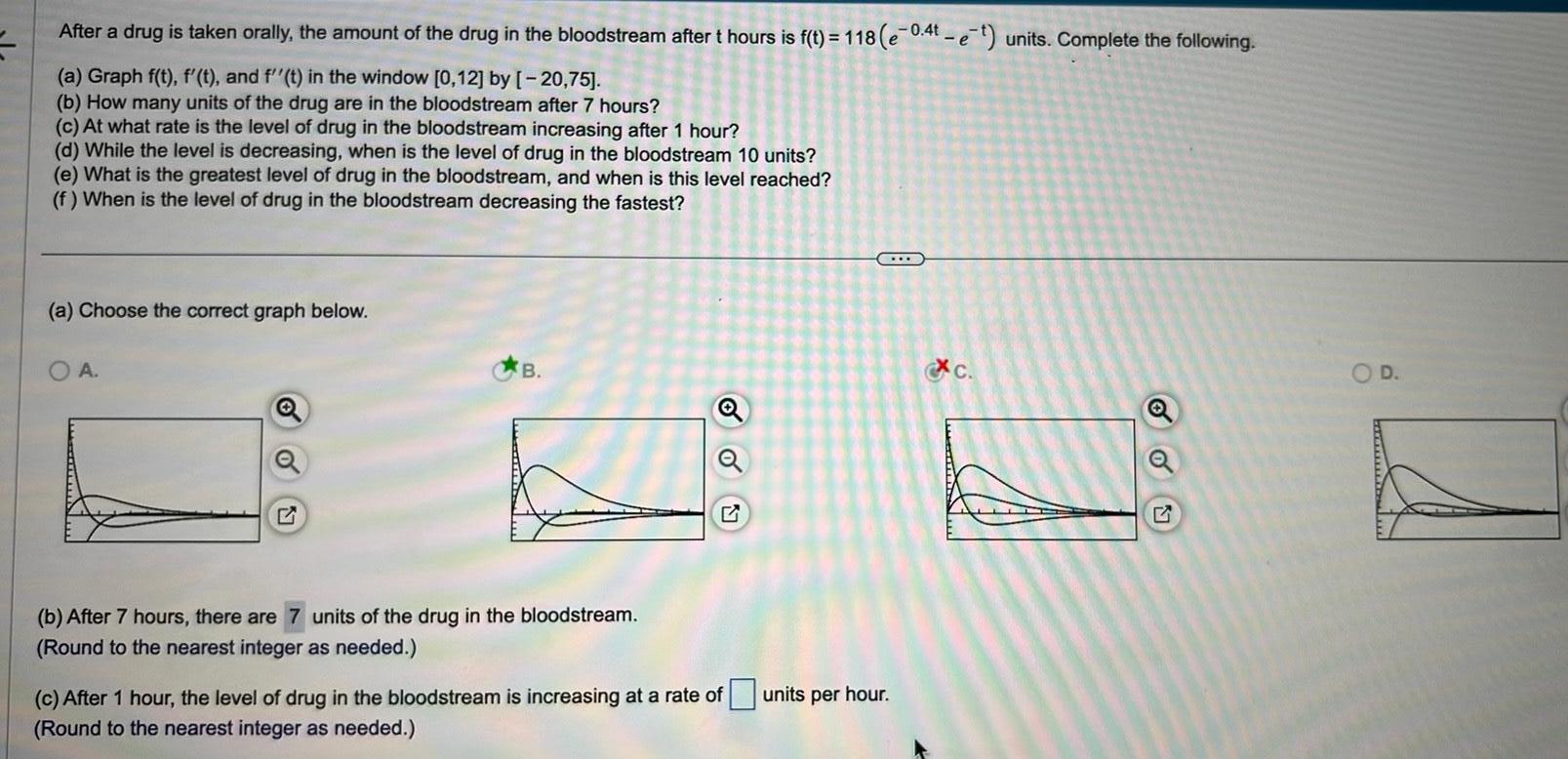
Application of derivativesAfter a drug is taken orally the amount of the drug in the bloodstream after t hours is f t 118 e 0 4t et units Complete the following a Graph f t f t and f t in the window 0 12 by 20 75 b How many units of the drug are in the bloodstream after 7 hours c At what rate is the level of drug in the bloodstream increasing after 1 hour d While the level is decreasing when is the level of drug in the bloodstream 10 units e What is the greatest level of drug in the bloodstream and when is this level reached f When is the level of drug in the bloodstream decreasing the fastest a Choose the correct graph below OA B b After 7 hours there are 7 units of the drug in the bloodstream Round to the nearest integer as needed c After 1 hour the level of drug in the bloodstream is increasing at a rate of Round to the nearest integer as needed units per hour c Q O D

Calculus
Application of derivativesFind the area of a triangle with sides of length 9 and 13 and included angle 56 48 499 32 713 86 730 Ono correct answer
Calculus
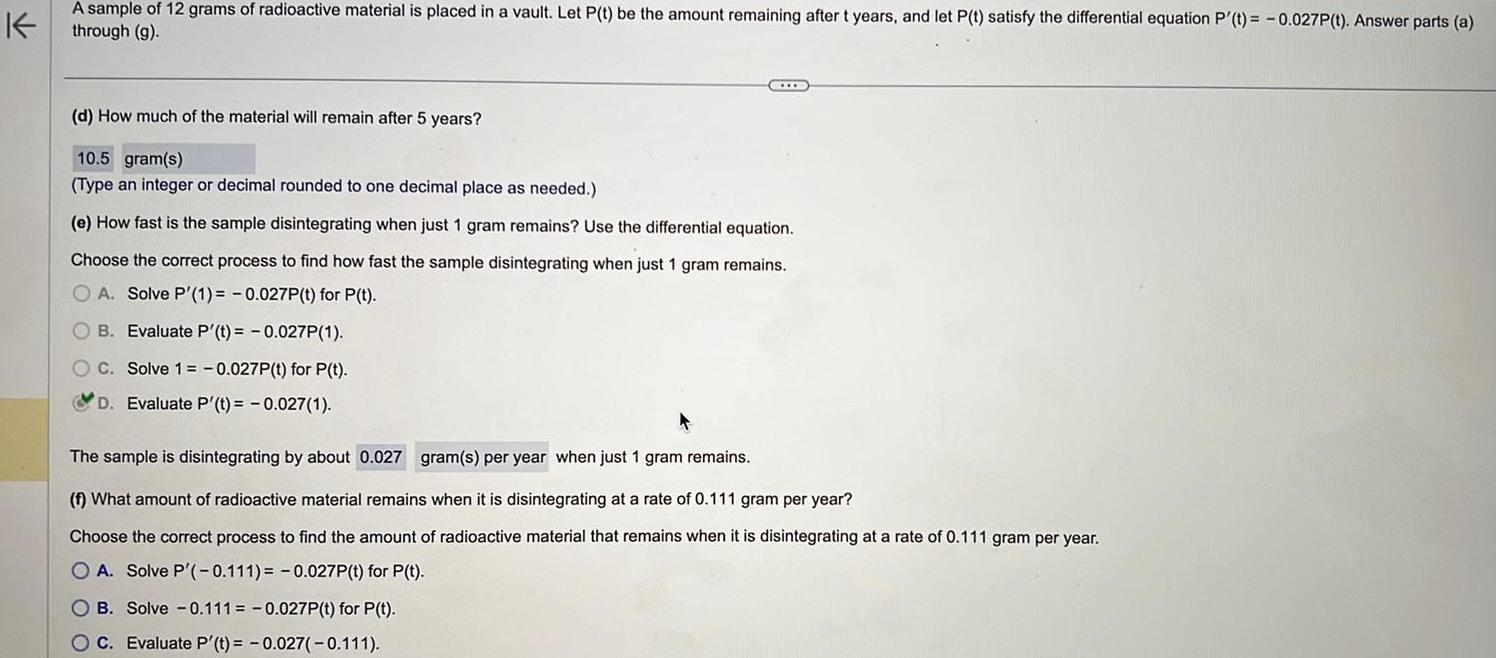
DifferentiationK A sample of 12 grams of radioactive material is placed in a vault Let P t be the amount remaining after t years and let P t satisfy the differential equation P t 0 027P t Answer parts a through g d How much of the material will remain after 5 years 10 5 gram s Type an integer or decimal rounded to one decimal place as needed e How fast is the sample disintegrating when just 1 gram remains Use the differential equation Choose the correct process to find how fast the sample disintegrating when just 1 gram remains OA Solve P 1 0 027P t for P t B Evaluate P t 0 027P 1 C Solve 1 0 027P t for P t D Evaluate P t 0 027 1 The sample is disintegrating by about 0 027 gram s per year when just 1 gram remains f What amount of radioactive material remains when it is disintegrating at a rate of 0 111 gram per year Choose the correct process to find the amount of radioactive material that remains when it is disintegrating at a rate of 0 111 gram per year OA Solve P 0 111 0 027P t for P t OB Solve 0 111 0 027P t for P t C Evaluate P t 0 027 0 111
Calculus
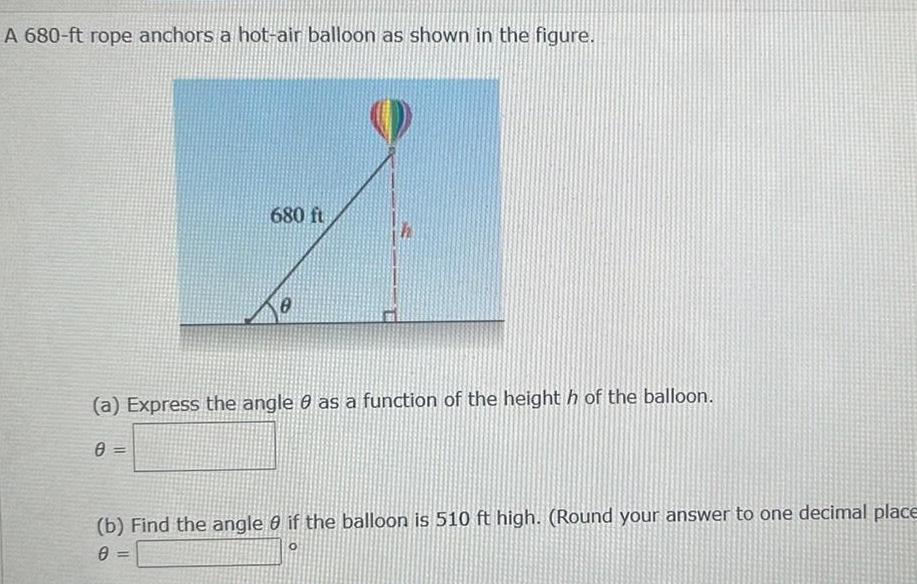
Application of derivativesA 680 ft rope anchors a hot air balloon as shown in the figure 680 ft 0 a Express the angle 0 as a function of the height h of the balloon 0 b Find the angle 0 if the balloon is 510 ft high Round your answer to one decimal place 0 O

Calculus
Application of derivativesA 40 ft pole casts a shadow as shown in the figure 40 ft a Express the angle of elevation of the sun as a function of the length s of the shadow 0 b Find the angle of elevation of the sun when the shadow is 25 ft long Round your answer to one decima 0

Calculus
Application of derivativesA 84 ft tree casts a shadow that is 110 ft long What is the angle of elevation of the sun Round your answer to one decimal place
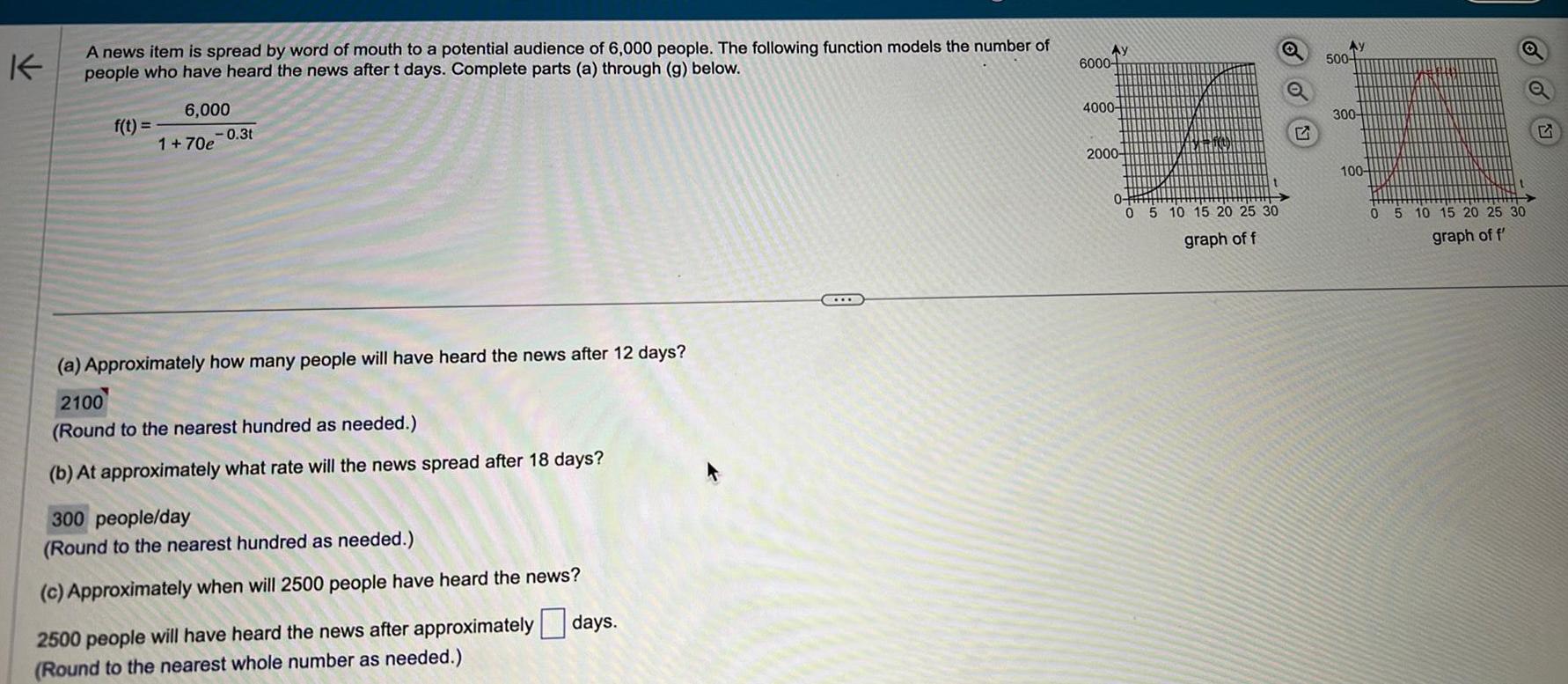
Calculus
Limits & ContinuityK A news item is spread by word of mouth to a potential audience of 6 000 people The following function models the number of people who have heard the news after t days Complete parts a through g below 6 000 1 70e 0 3t f t a Approximately how many people will have heard the news after 12 days 2100 Round to the nearest hundred as needed b At approximately what rate will the news spread after 18 days 300 people day Round to the nearest hundred as needed c Approximately when will 2500 people have heard the news 2500 people will have heard the news after approximately Round to the nearest whole number as needed days Ay 6000 4000 2000 0 0 5 10 15 20 25 30 graph of f Q G Ay 500 300 100 oo 0 5 10 15 20 25 30 graph of f E

Calculus
Differential equationsblem 4 When a bacteria colony reaches 150 thousand it is treated with antibiotics Due to the antibiotics the bacteria population decreases by 10 each week a Find an exponential model B t that approximates the bacteria population in thousands after t weeks b Estimate the bacteria population to the nearest thousand after 3 5 weeks c Use limits to explain what will happen to the bacteria population as time continues to increase d Sketch the graph of B t Label and appropriately scale the axes to include the entire graph

Calculus
Differential equationsDetermining values of 6 from a graph The function f in the fig ure satisfies lim f x 5 Determine the largest value of 8 0 x 2 satisfying each statement a If 0 x2 8 then f x 5 2 b If 0 x2 8 then f x 5 1
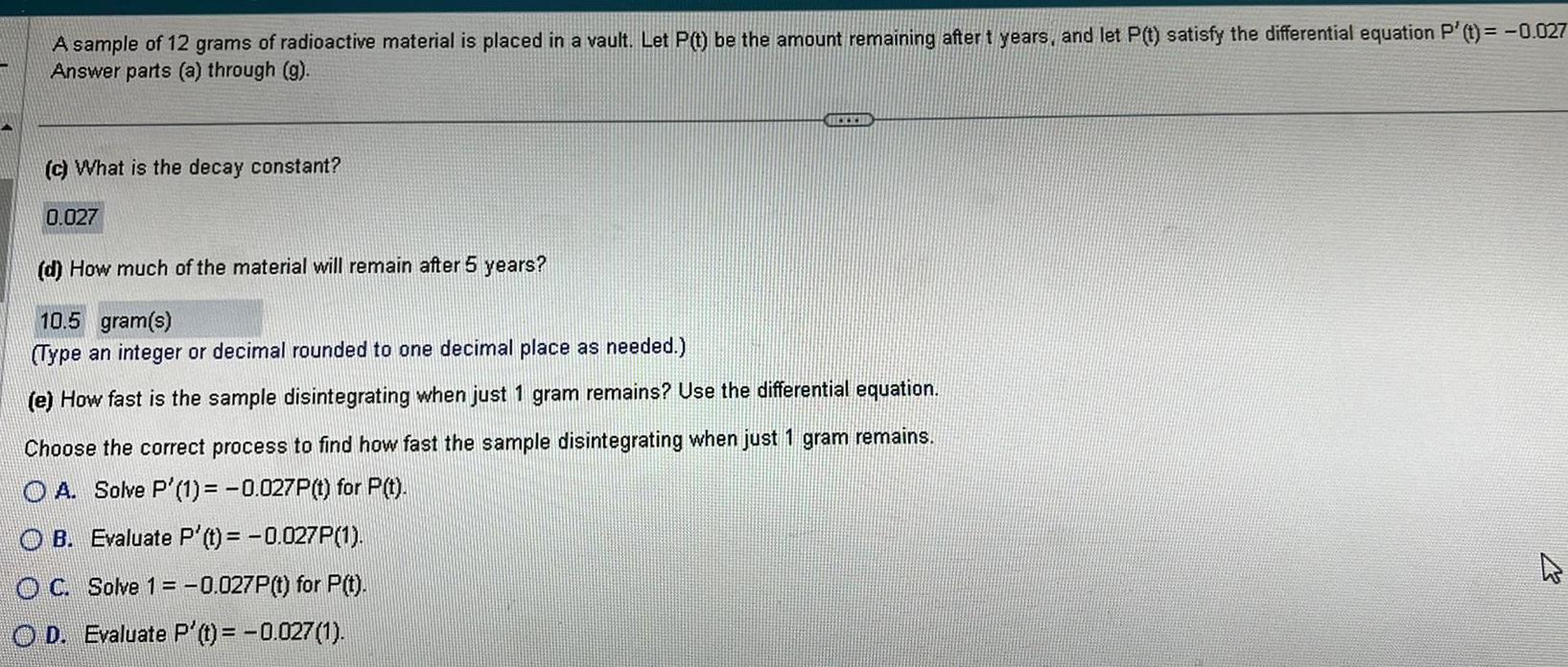
Calculus
Application of derivativesA sample of 12 grams of radioactive material is placed in a vault Let P t be the amount remaining after t years and let P t satisfy the differential equation P t 0 027 Answer parts a through g c What is the decay constant 0 027 d How much of the material will remain after 5 years 10 5 gram s Type an integer or decimal rounded to one decimal place as needed e How fast is the sample disintegrating when just 1 gram remains Use the differential equation Choose the correct process to find how fast the samp disintegrating when just 1 gram remains OA Solve P 1 0 027P t for P t OB Evaluate P t 0 027P 1 OC Solve 1 0 027P t for P t OD Evaluate P t 0 027 1 D

Calculus
Application of derivativesThe price of a particular crop per bushel at time t in months is approximated by f t 8 0 002t 0 02e t What is the percentage rate of change of f t at t 0 t 1 t 2 HELLER The price of the crop is expected to change at a relative rate of 0 22 per month when t 0 Do not round until the final answer Then round to two decimal places as needed The price of the crop is expected to change at a relative rate of per month when t 1 Do not round until the final answer Then round to two decimal places as needed

Calculus
Differential equationsind an equation of the tangent line to the graph of y g x at x 6 if g 6 3 and g 6 5 Enter your answer as an equation in terms of y and x X Enhanced Feedback Please try again Remember the slope of g at x is the derivative function g x Use the point of intersection along with the slope to find an equation for the tangent line
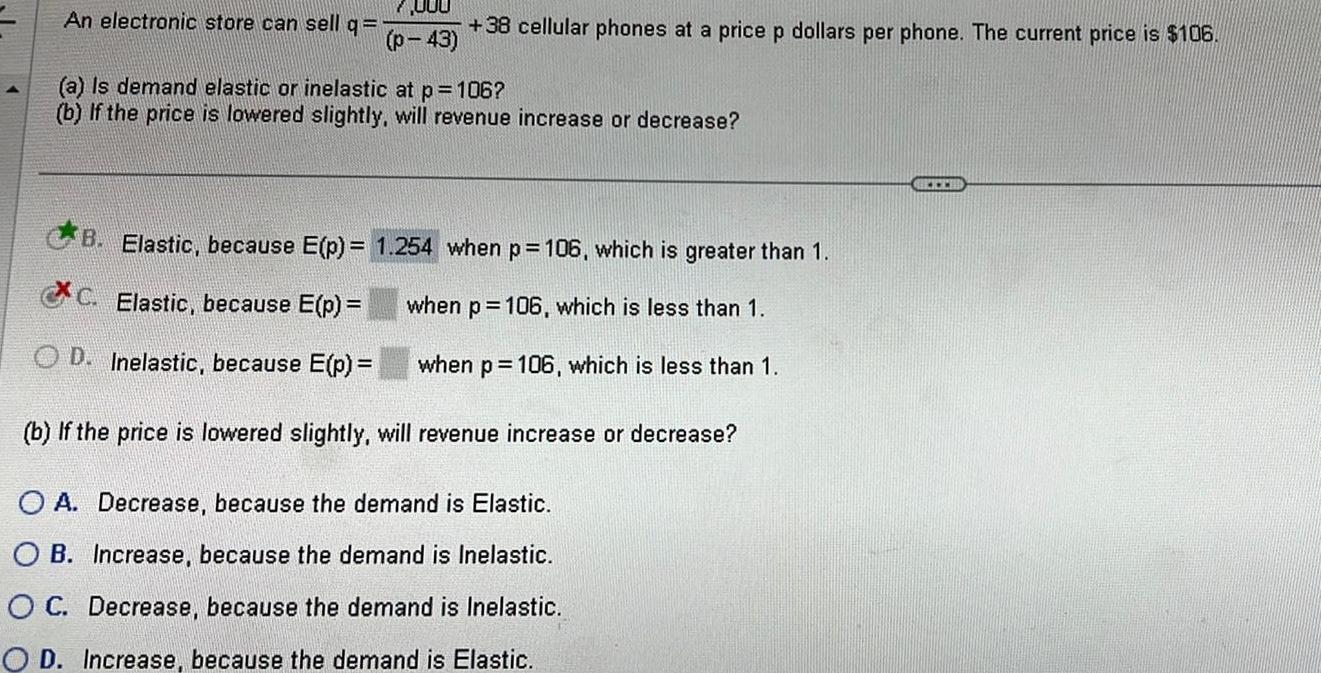
Calculus
Definite Integrals000 p 43 An electronic store can sell q 1 38 cellular phones at a price p dollars per phone The current price is 106 a Is demand elastic or inelastic at p 106 b If the price is lowered slightly will revenue increase or decrease B Elastic because E p C Elastic because E p OD Inelastic because E p b If the price is lowered slightly will revenue increase or decrease O A Decrease because the demand is Elastic OB Increase because the demand is Inelastic OC Decrease because the demand is Inelastic OD Increase because the demand is Elastic 1 254 when p 106 which is greater than 1 when p 106 which is less than 1 when p 106 which is less than 1 www

Calculus
Application of derivatives20 Points t a t 1 t 2 t 3 V The displacement in meters of a particle moving in a straight line is given by the equation of motion s 5 t2 where t is measured in seconds Find the velocity of the particle at times t a t 1 t 2 and t 3 V V DETAILS V m s SCALCET8 2 7 015 m s m s m s MY NOTES PRACTICE ANC

Calculus
Application of derivatives49 60 Evaluate each limit 4x 10 49 lim x2 V 2x 51 lim X T cos x 3 cos x 2 cos x 1 53 lim 7 x 3 55 lim 57 lim sin x 1 2 Vsin x 1 2 cos x 1 x 0 sin x 1 59 lim 2 0 1 50 lim x 4 x 9 x 1 52 lim X 3 2 54 lim 56 lim 0 0 X 1 5 21 V 5 1 2 58 lim x 0 60 lim sin x 6 sin x 5 sin x 1 1 2 sin 0 sin 0 1 cos x sin x In x 5 ln x 6 In x 2


Calculus
Indefinite IntegrationFind all angles 8 between 0 and 180 satisfying the given equation Round your answer to one decimal place Enter your answers as a comma separated list Enter your answer in degrees sin 8 H 6
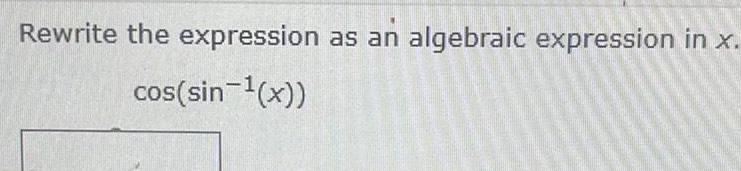
Calculus
Application of derivativesRewrite the expression cos sin x as as an algebraic expression in x an

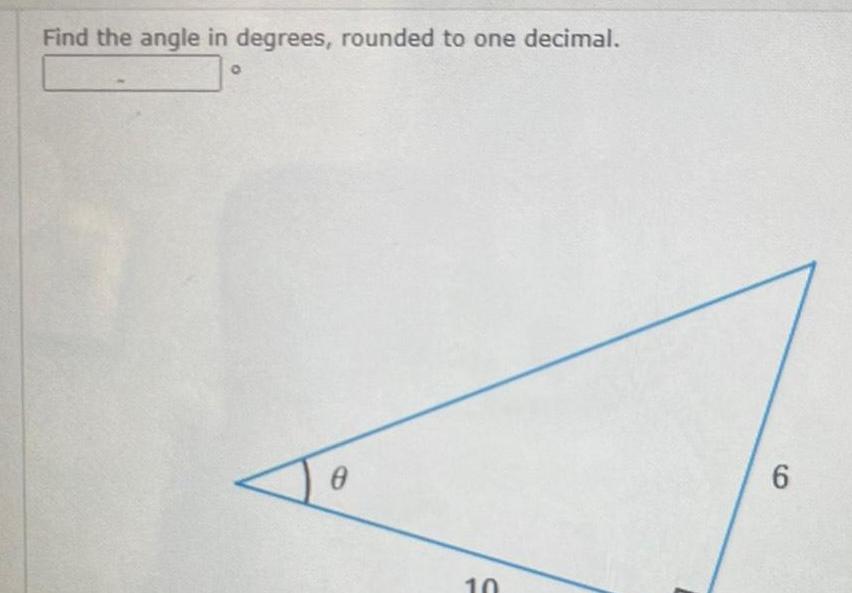
Calculus
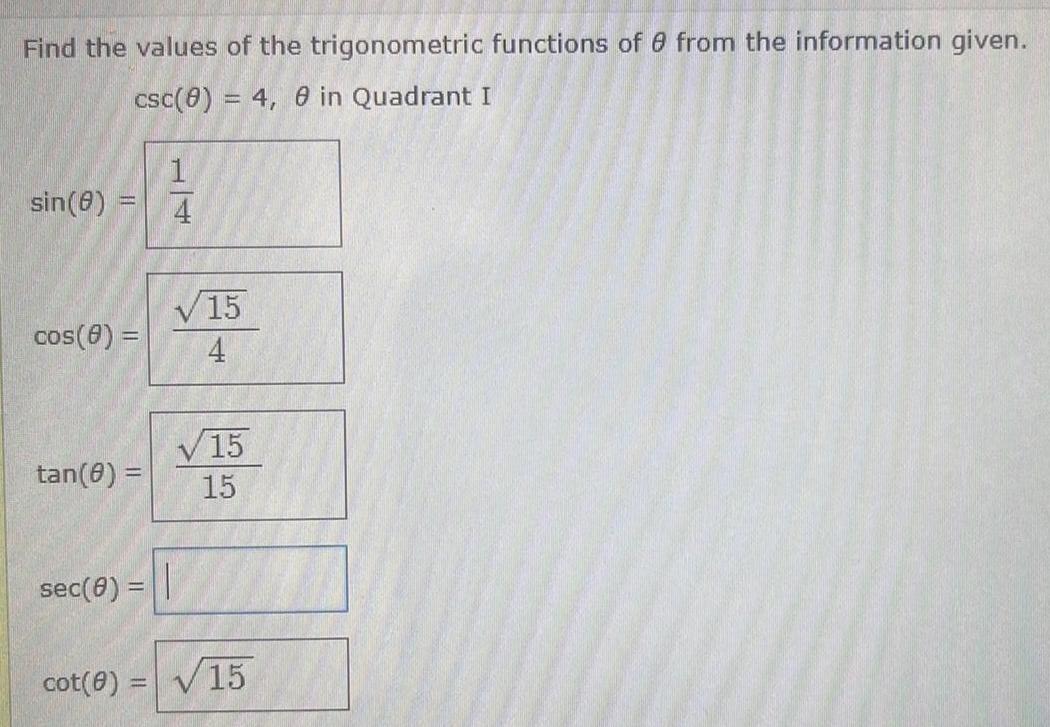
Definite IntegralsFind the values of the trigonometric functions of 8 from the information given csc 0 4 8 in Quadrant I sin 8 cos 8 tan 8 sec 0 cot 0 1 4 15 4 15 15 15

Calculus
Differential equations41 48 Functions with roots Determine the interval s on which the following functions are continuous At which finite endpoints of the intervals of continuity is f continuous from the left or continuous from the right 41 f x 5 x 43 f x 2x 16 45 f x x 2x 3 47 f x 2x 3 2 3 42 f x 25 x 44 f x x 3x 2 46 f t t 1 3 2 48 f z z 1 3 4

Calculus
Definite Integralsopen interval I gives rise to the succession of derivatives 9 dX d x d X dt dt dt Now a differential equation in the function X t is therefore an equation of the type X MATHEMATICS F1 X du x X dX d X dt d 2 du x x 1 i n Such an equation is said to be an ordinary differential equation Thus an ordinary differential equation is a differential equation in which the constituent function X X t is a function of a single real variable Tim We often use the acronym ODE in place of the full term ordinary differential equation j1 i j n D u de X dik II On the other hand there are differential equations in a function u xu x of a real multivariable x x x x which ranges in an open subset of R Such a function u u x gives rise to mixed partial derivatives 0 Fx u 1 GJEJ 65 for various multi indices a a a with o Zi 0 1 2 the mixed partial derivative D u having the order a o 0 Now a differential equation in such a function u ux of a multi variable x x ranging in an open subset of R is an equation of the type du d u Du o m 0 2 x x dx its order being m Equation 2 is said to be a partial differential equation in u x because it involves the mixed partial derivatives of u We use the acronym PDE for this type of differential equations There is more about the setting of a differential equation In a mathematical problem a differential equation is accompanied by auxiliary data A solution of a differential equation is required to satisfy this auxiliary data To be more specific we are given a subset of the domain of a prospective solution and some of its derivatives of the solution at the points of this subset
Calculus
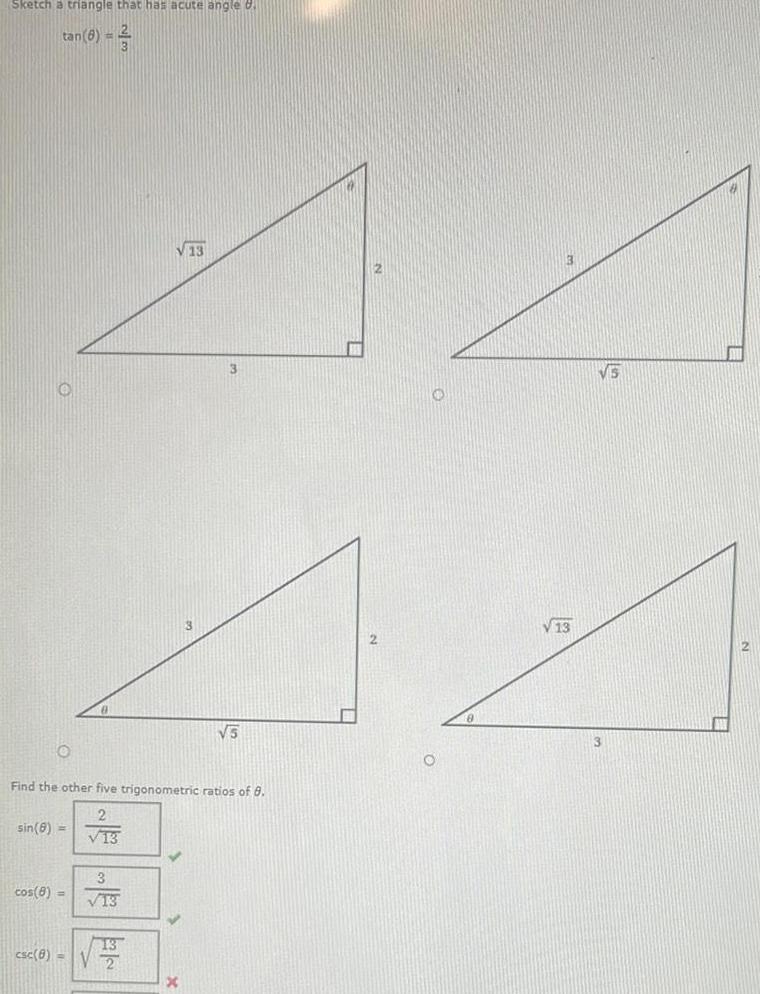
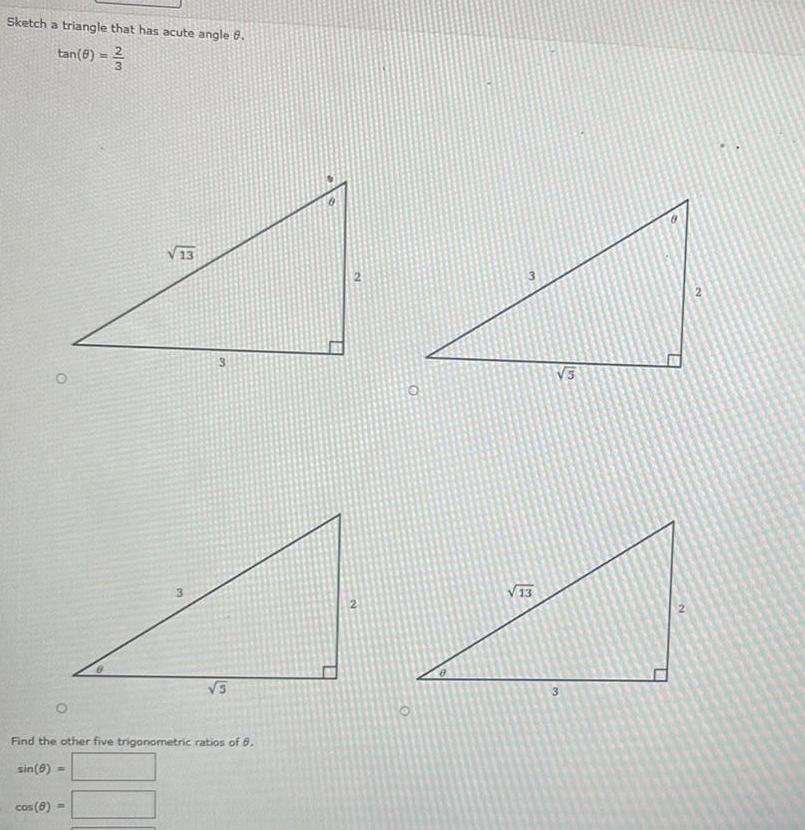
Vector CalculusSketch a triangle that has acute angle tan 6 O Find the other five trigonometric ratios of 8 2 13 sin 8 cos 8 3 13 13 csc 8 2 5 x V 13 VS IN
Calculus
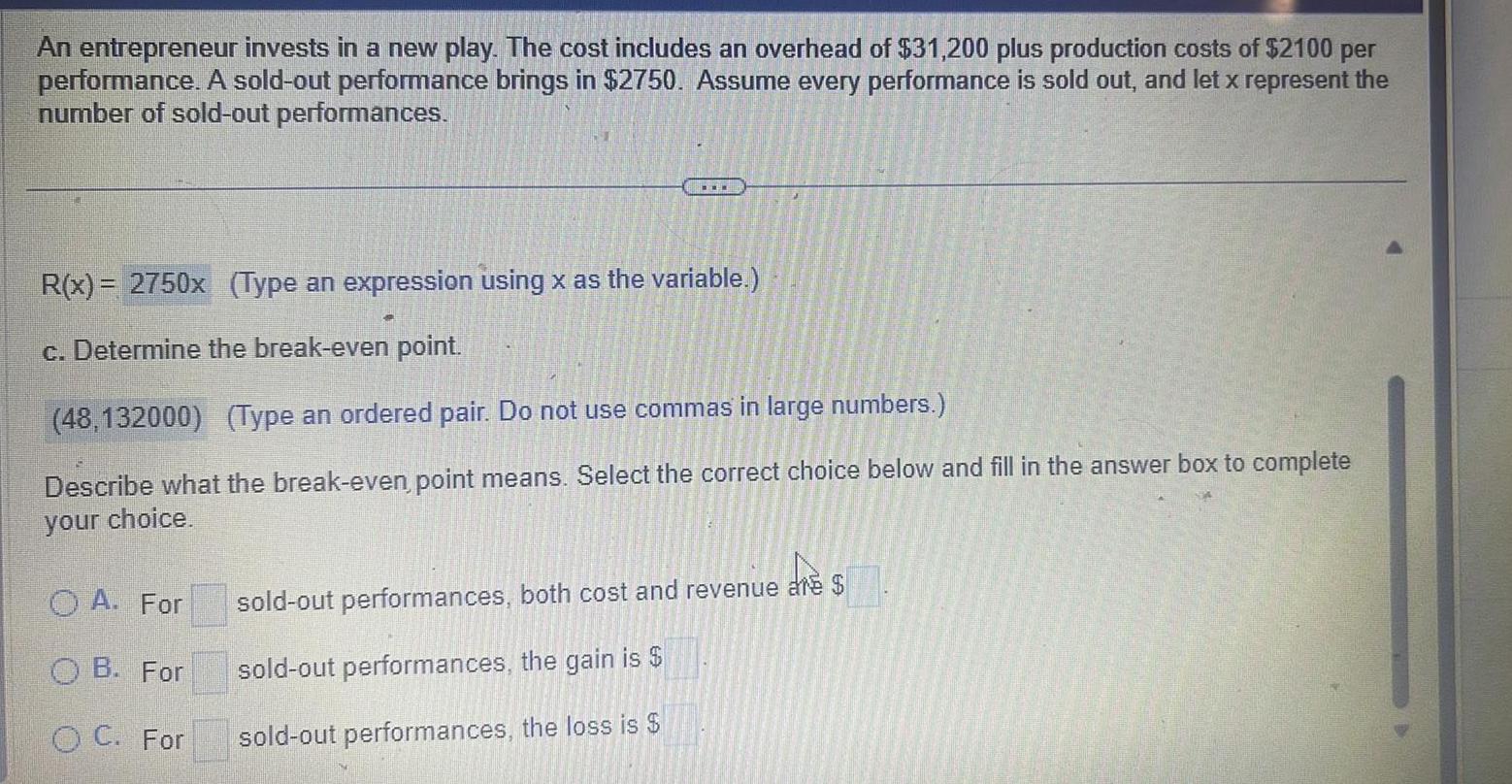
Application of derivativesAn entrepreneur invests in a new play The cost includes an overhead of 31 200 plus production costs of 2100 per performance A sold out performance brings in 2750 Assume every performance is sold out and let x represent the number of sold out performances R x 2750x Type an expression using x as the variable c Determine the break even point 48 132000 Type an ordered pair Do not use commas in large numbers Describe what the break even point means Select the correct choice below and fill in the answer box to complete your choice O A For OB For O C For sold out performances both cost and revenue are sold out performances the gain is sold out performances the loss is

Calculus
Application of derivativesProblem 3 Let f x 7e a What are the domain and range of f b Find any asymptotes on the graph f c Find any x or y intercepts on the graph of f d Evaluate the average rate of change of f over the intervals 2 1 an

Calculus
Limits & ContinuityThe angle of elevation to the top of a very tall Building is found to be 8 from the ground at a distance of 1 mi from the base of the building Using this information find the height of the building Round your answer to the nearest foot ft

Calculus
DifferentiationA man is lying on the beach flying a kite He holds the end of the kite string at ground level and estimates the angle of elevation of the kite to be 50 If the string is 400 ft long how high is the kite above the ground Round your answer to the nearest foot Need Help MY NOTES PRACTICE ANOTH
Calculus
Indefinite IntegrationSketch a triangle that has acute angle 8 tan 8 O cos 8 3 12 3 3 Find the other five trigonometric ratios of 8 sin 6 3 O 3 13 3 Cal N

Calculus
DifferentiationA 21 ft ladder leans against a building so that the angle between the ground and the ladder is 66 How high does the ladder reach on the building Round your answer to the nearest foot ft
Calculus
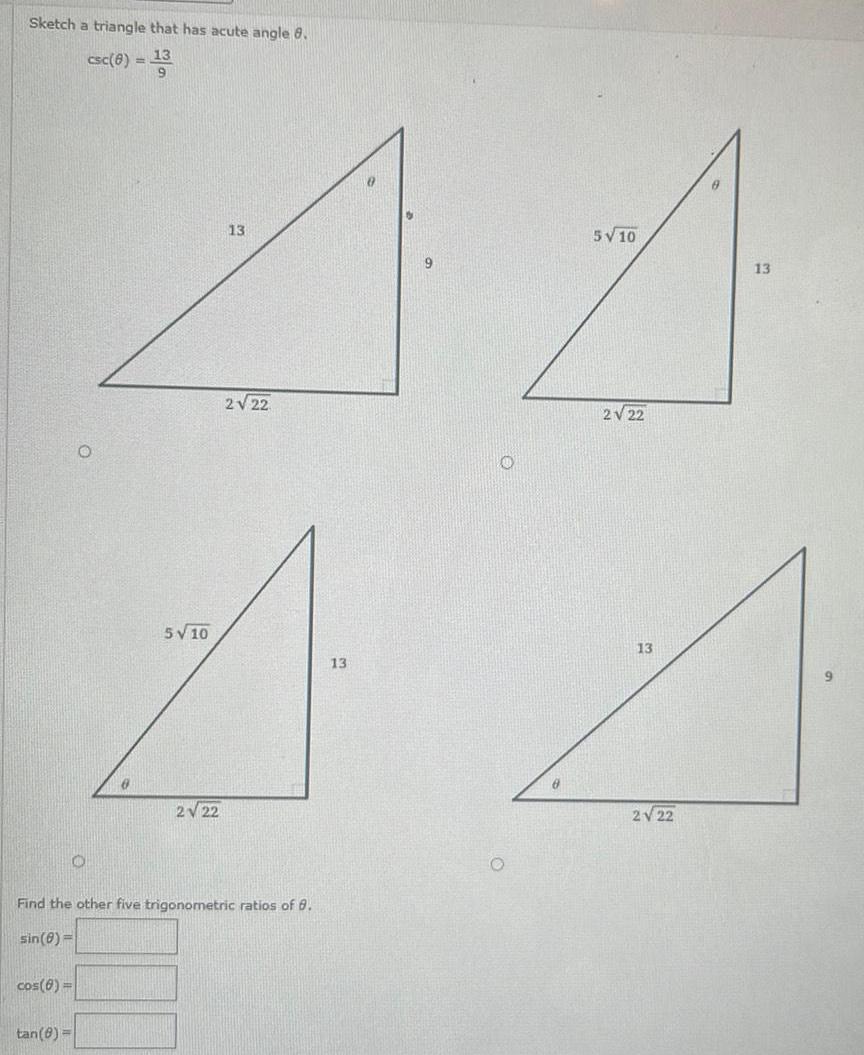
Application of derivativesSketch a triangle that has acute angle 8 13 csc 8 13 5 10 13 2 22 2 22 A A A A 5 10 13 13 2 22 2 22 O cos 8 O Find the other five trigonometric ratios of 8 sin 8 tan 8 9 O