Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
Definite Integralsn limno 2 1 k 1 n 4 O A 2 2x dx O B 2 x dx 4 c 2 x dx 2 O D 2 2x dx O E 2 x dx

Calculus
Vector CalculusCalculus AB Assignment Applications of the Derivative I A Find an equation that relates the total length of the elastic x to the distance y that the button has moved

Calculus
Application of derivatives6 At a certain instant the base of a triangle is 5 inches and is increasing at the rate of 1 inch per minute At the same instant the height is 10 inches and is decreasing at the rate of 2 5 inches per minute Is the area of the triangle increasing or decreasing Justify your answer

Calculus
Application of derivatives1 A candy company needs a custom box for their truffles The box they ve chosen is in the shape of a cylinder with a hemisphere of the same radius on top The total volume of the box is v 1 2 4 y 7 where y is the height of the box and is the radius of the box Originally the candy box was designed to have a height of 6 inches and a radius of 2 inches but the shipper suggests that the boxes be made slightly shorter You now need to adjust the radius so that the height is reduced to 5 75 inches but the volume remains constant A Find the value of at the point r 2 y 6 I

Calculus
Vector Calculus3 If a right triangle has legs 6 and 8 its hypotenuse is 10 The triangle will be inscribed within a circle with area 25T The hypotenuse will be the diameter of the circle B Use a tangent line approximation to estimate the area of the circumscribed circle Now consider the sphere that just contains the triangle so the hypotenuse is the diameter of the sphere Use a tangent line approximation to estimate the volume of this sphere

Calculus
Vector CalculusWhich of the following statements are always true for any pair of nonzero vectors v and w Select all that apply v w is a vector orthogonal to both v and w O v w is a number If is the angle between v and w then cos 0 V W v w
Calculus
Vector CalculusWhich of the following equations are true for any two nonzero orthogonal vectors u and v in space Select all that apply u v u v Oux v 0 0 ux v u v u v 0
Calculus
Vector CalculusWhich of the following statements apply to any unit vector u in space Select all that apply O cu c for every number c u u 1 Ou 1 u 0
Calculus
Vector CalculusTwo equivalent vectors always have the the same select all that apply O direction terminal point O magnitude initial point

Calculus
Application of derivativesEvaluate the following definite integral by interpretir 5 S 2 2 3x dx OA 24 OB 17 5 O C 12 5 OD 37 5 OE 75 0
Calculus
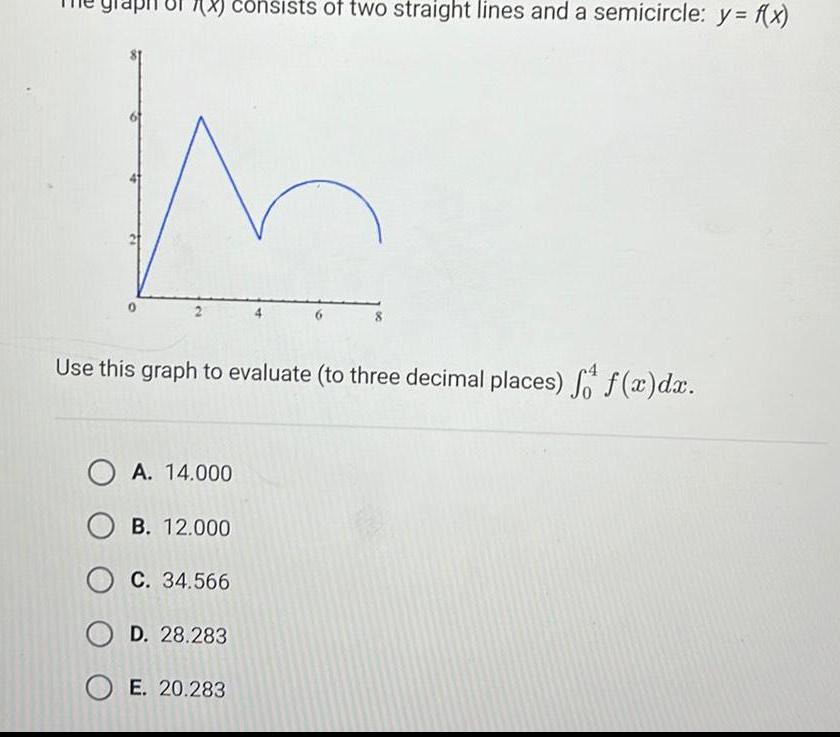
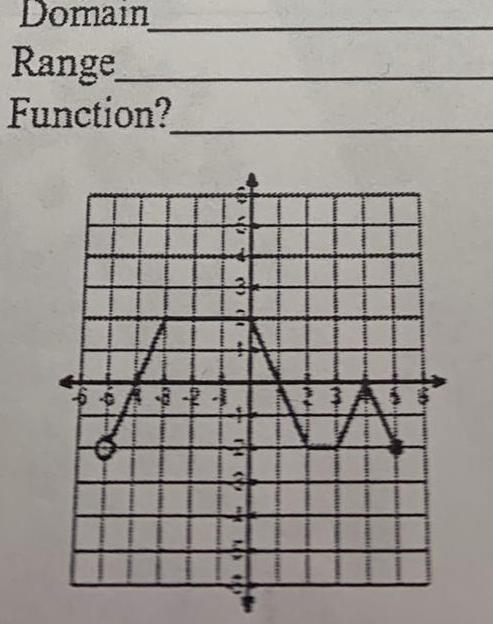
Indefinite Integration181 consists of two straight lines and a semicircle y f x 2 Use this graph to evaluate to three decimal places f f x dx OA 14 000 OB 12 000 C 34 566 D 28 283 OE 20 283
Calculus
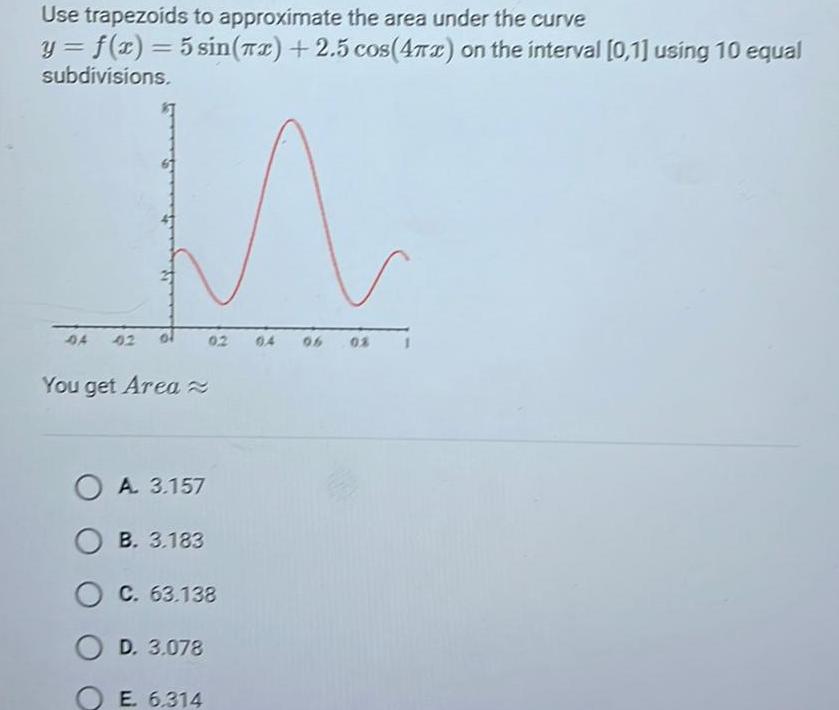
Definite IntegralsUse trapezoids to approximate the area under the curve y f x 5 sin x 2 5 cos 4x on the interval 0 1 using 10 equal subdivisions 04 42 You get Area 0 2 OA 3 157 OB 3 183 C 63 138 OD 3 078 E 6 314 06 08
Calculus
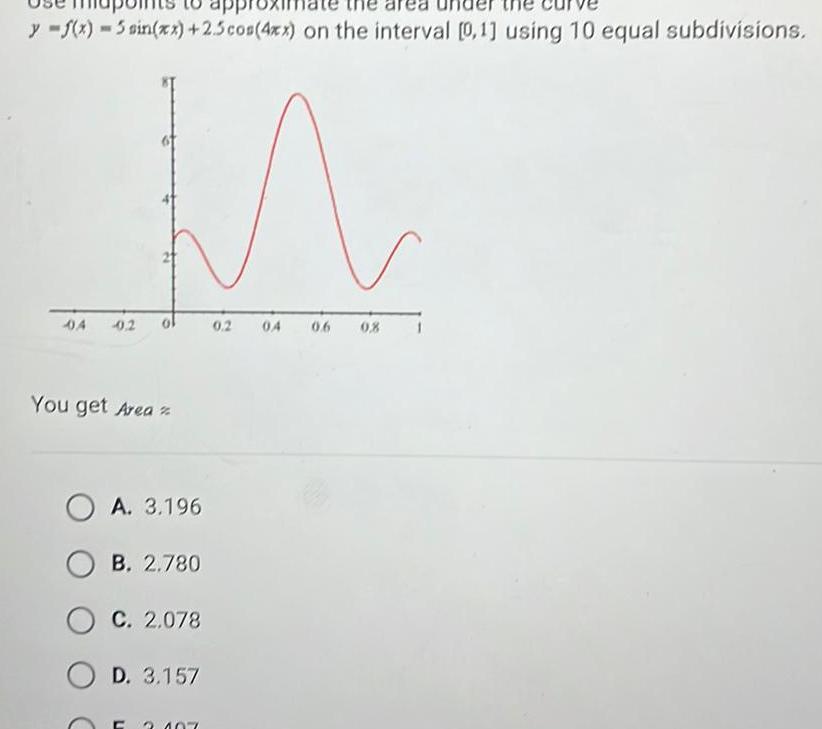
Definite Integralsy f x 5 sin xx 2 5 cos 4xx on the interval 0 1 using 10 equal subdivisions M 04 0 2 You get Area OA 3 196 B 2 780 C 2 078 OD 3 157 C 3 107 0 2 04 06 0 8
Calculus
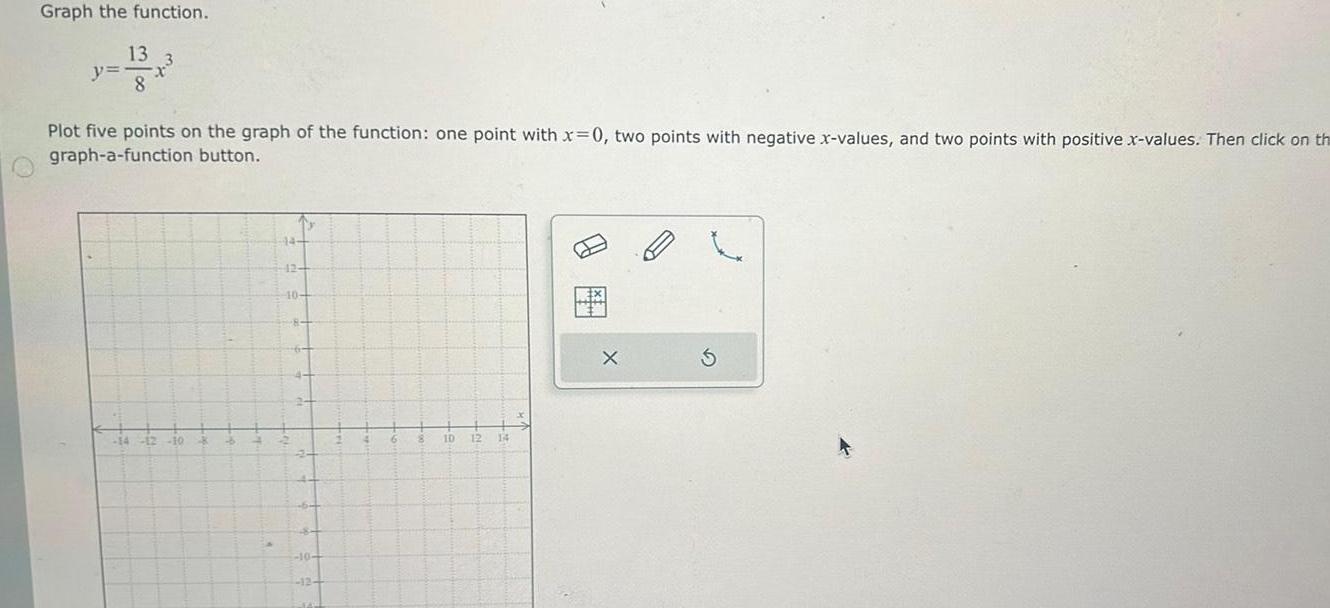
Application of derivativesGraph the function y 13 8 Plot five points on the graph of the function one point with x 0 two points with negative x values and two points with positive x values Then click on th graph a function button 14 12 10 12 10 12 14 X


Calculus
Application of derivativesLeila Dan and Reuben sent a total of 124 text messages over their cell phones during the weekend Dan sent 9 fewer messages than Leila Reuben sent 3 times as many messages as Dan How many messages did they each send Number of text messages Leila sent Number of text messages Dan sent Number of text messages Reuben sent 0 0 E X S
Calculus
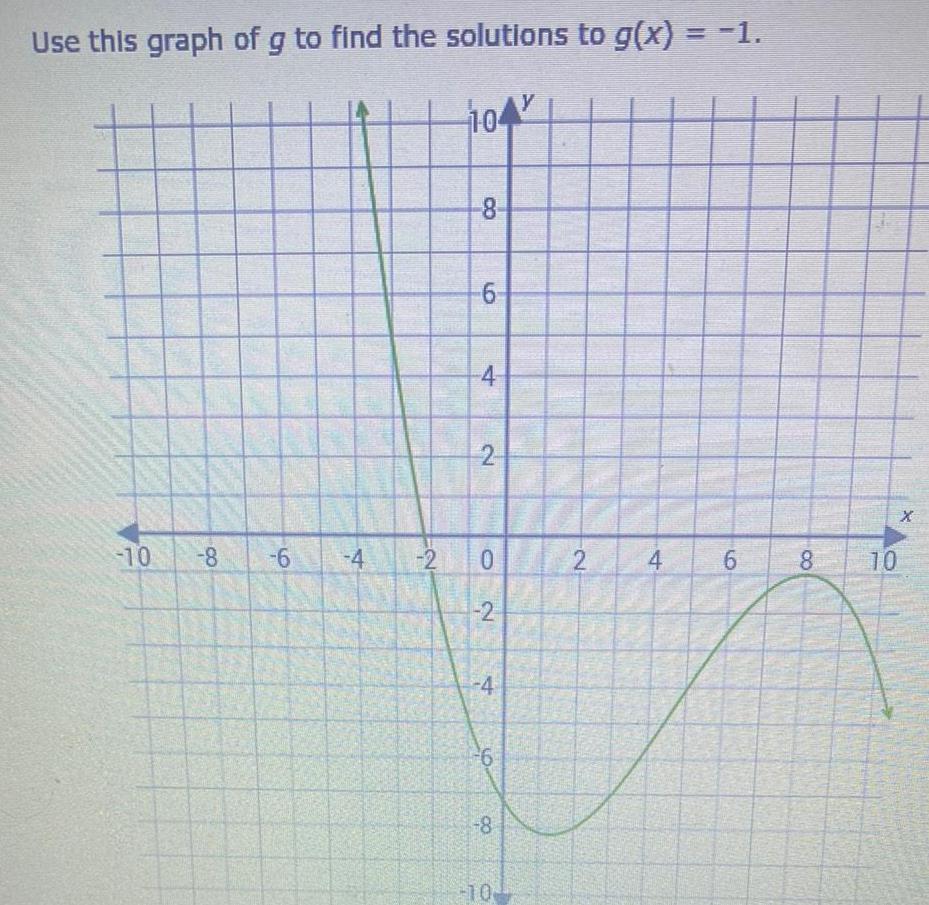
Vector CalculusUse this graph of g to find the solutions to g x 1 10 8 9 6 4 2 104 8 6 4 2 0 2 4 6 8 10 y 2 4 6 8 10 X
Calculus
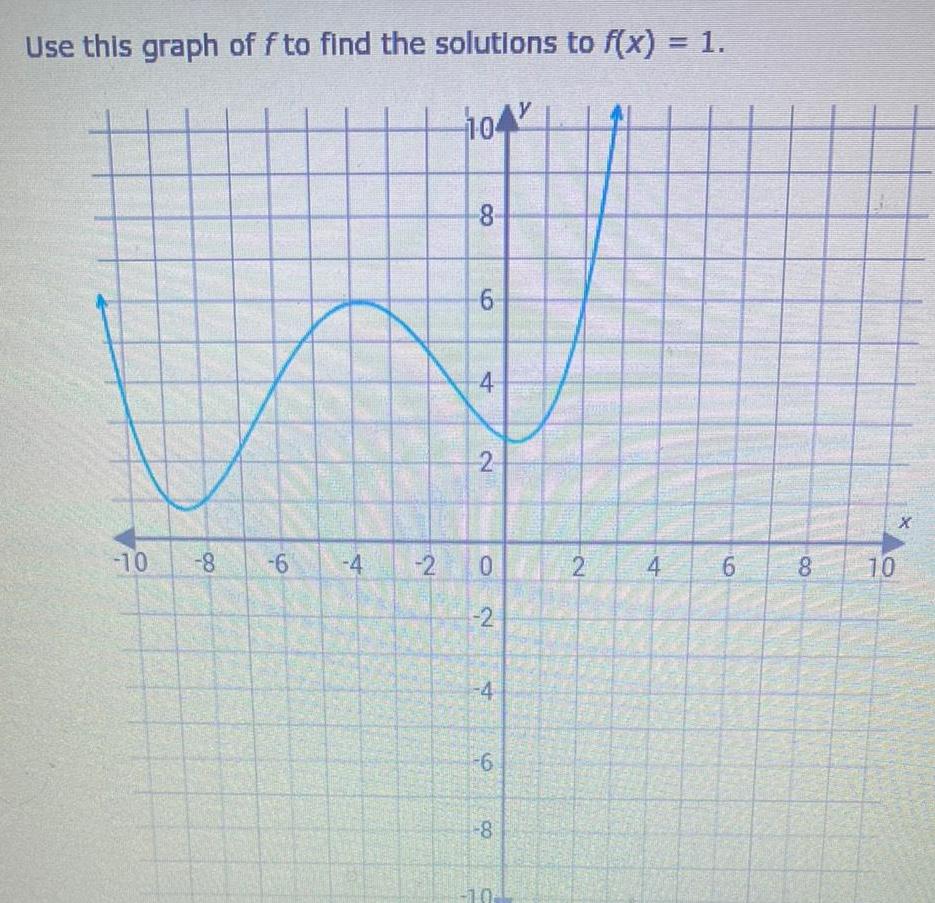
DifferentiationUse this graph of f to find the solutions to f x 1 104 10 8 6 4 2 8 6 4 2 0 2 4 6 8 G 2 4 6 8 Ag 10

Calculus
Application of derivatives4 Suppose the point 4 is on the curve sinx siny C where C is a constant Use x y the tangent line approximation to find the y coordinate of the point on the curve with x coordinate 10 Be sure to show all your work

Calculus
DifferentiationUse tangent line approximation to estimate 2390 to seven decimal places recognizing that 7 2401 Show all your work
Calculus
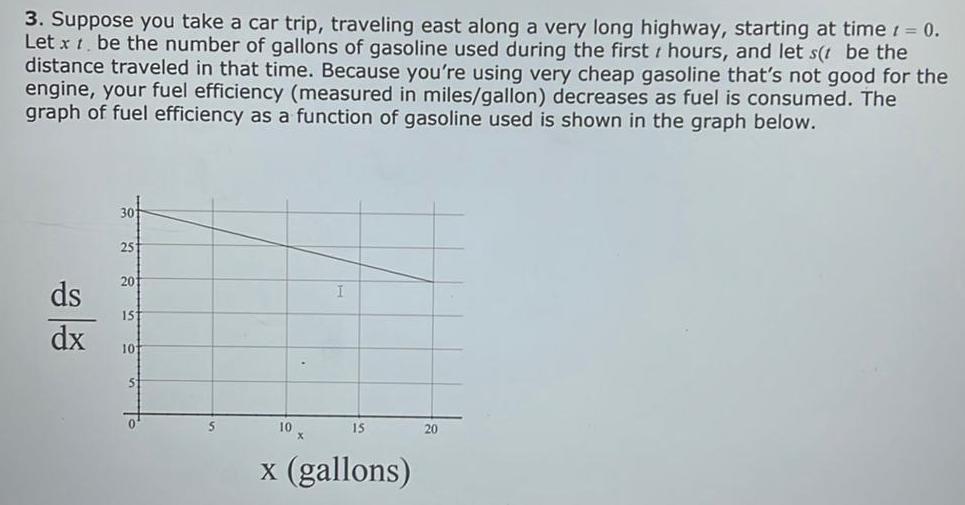
Vector Calculus3 Suppose you take a car trip traveling east along a very long highway starting at time 1 0 Let x t be the number of gallons of gasoline used during the first hours and let s t be the distance traveled in that time Because you re using very cheap gasoline that s not good for the engine your fuel efficiency measured in miles gallon decreases as fuel is consumed The graph of fuel efficiency as a function of gasoline used is shown in the graph below ds dx 25 201 151 101 5 5 I 10x x gallons 15 20

Calculus
Application of derivatives2 A boat is pulled into a dock by a rope with one end attached to the front of the boat and the other end passing through a ring attached to the dock at a point 5 feet higher than the front of the boat The rope is being pulled through the ring at the rate of 0 6 feet per second How fast is the boat approaching the dock when 13 feet of rope are out

Calculus
Vector CalculusSuppose your friend gives you the following problem There is some function p x that represents profit p in dollars as a function of the number of units sold x Your friend doesn t know what the function p x is explicitly but does know that p x 2 for all x Your friend also knows that p 200 3175 24 Now your friend has enough information to approximate p 203 using tangent line approximation but your friend really wants to know how accurate that approximation will be The question to you then is What can you tell your friend about the accuracy of the tangent line approximation for p 203 given the above information about the function p You may explain yourself mathematically or by presenting graphs or just by discussing in complete sentences
Calculus
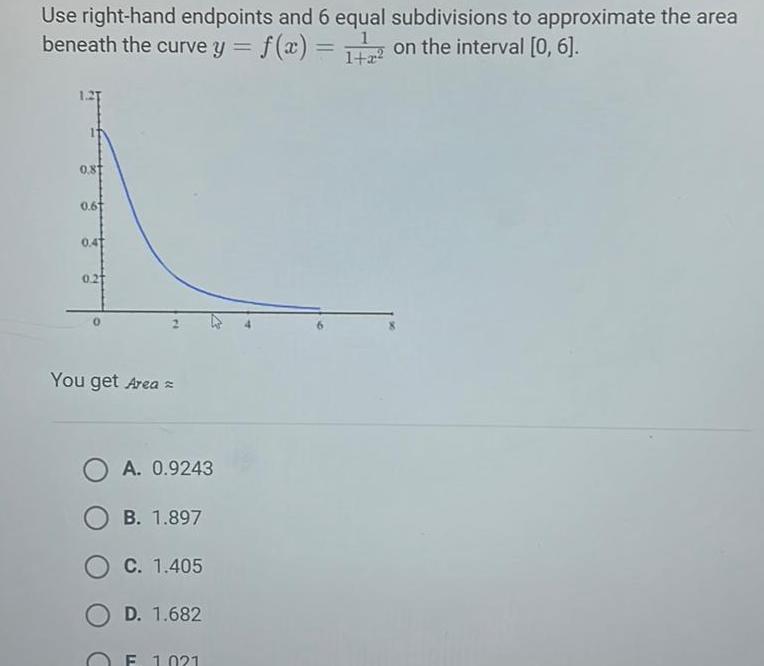
Definite IntegralsUse right hand endpoints and 6 equal subdivisions to approximate the area beneath the curve y f x 1 on the interval 0 6 1 2 0 81 0 61 0 41 0 21 You get Area A 0 9243 B 1 897 C 1 405 D 1 682 1 021

Calculus
Differentiation5 Use tangent line approximation to derive an estimate for 1 x when x is near 0 and n is any real number

Calculus
Definite Integrals4 A rotating beacon is located 2 miles out in the water Let 4 be the point on the shore that s closest to the beacon As the beacon rotates at 10 revolutions per minute the beam sweeps down the shore once each time it revolves Assume that the shore is straight How fast is the point where the beam hits the shore moving at an instant when the beam is lighting up a point 2 miles downshore from point
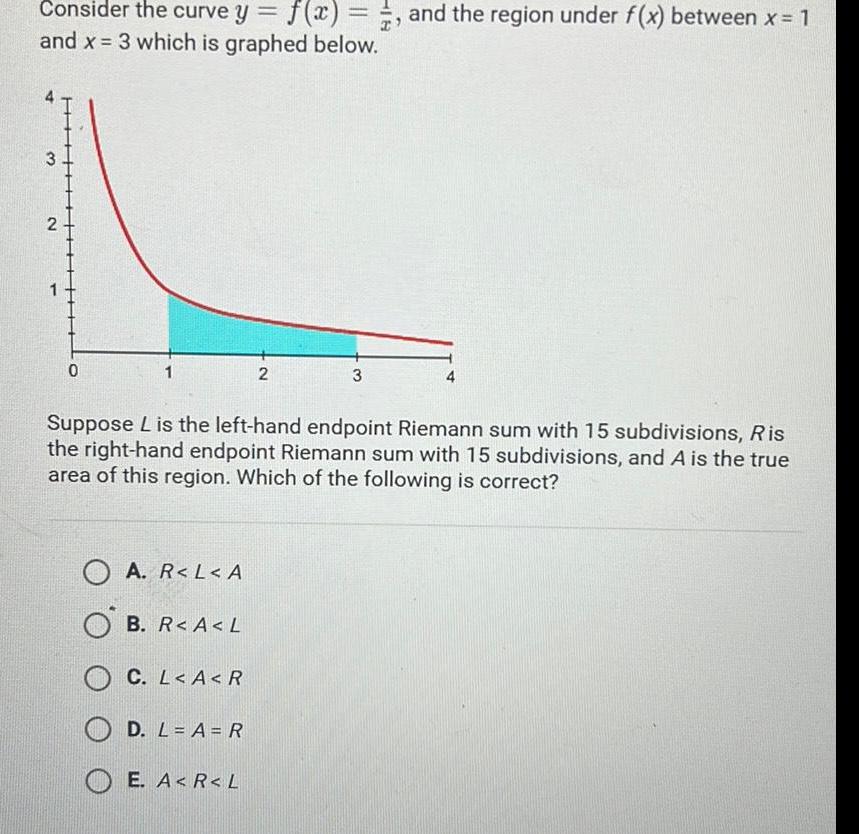
Calculus
Application of derivativesConsider the curve y f x and the region under f x between x 1 and x 3 which is graphed below 3 2 0 A R L A OB R A L C L A R Suppose L is the left hand endpoint Riemann sum with 15 subdivisions Ris the right hand endpoint Riemann sum with 15 subdivisions and A is the true area of this region Which of the following is correct D L A R 2 E A R L 3

Calculus
Application of derivatives1 At a certain instant the length of a rectangle is 3 inches and is increasing at the rate of 1 inch per minute At the same instant the width is 2 inches and is decreasing at the rate of 5 inches per minute Is the area increasing or decreasing
Calculus
Vector Calculus2 You measure a cubic container and find it to be about 10 cm on each side From this you conclude that it holds 1000 cc However your measurement is accurate only to within 10 1 cm So you can be sure that the side is between 9 9 and 10 1 cm A What are x f x and a in this problem B Use the tangent line approximation to estimate the error in your value of 1000 for the volume I C Give the percent error in your measurement of the length of the side
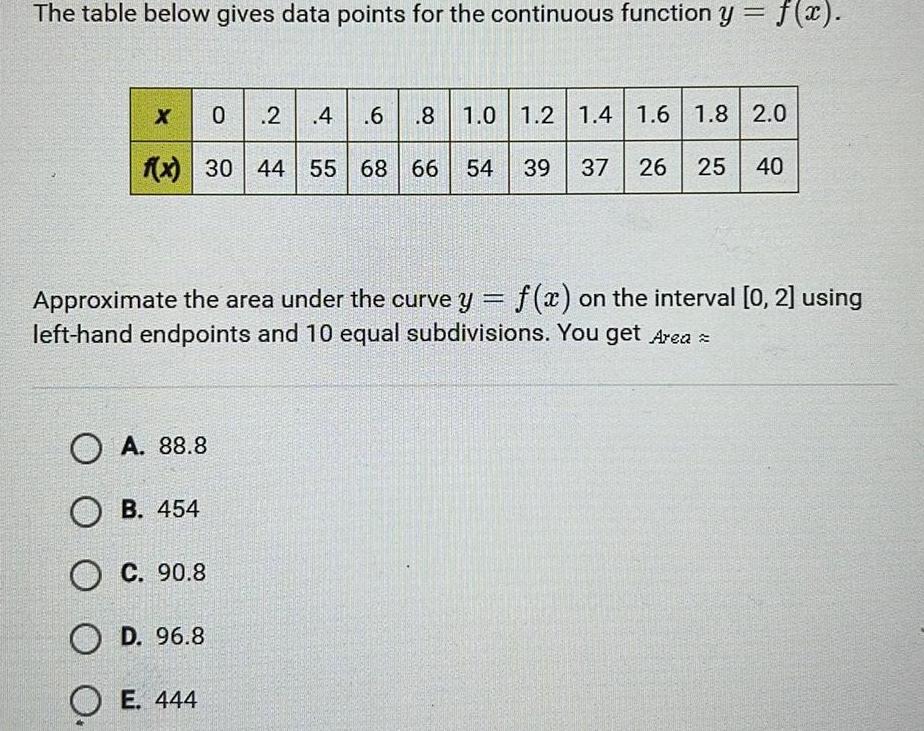
Calculus
Definite IntegralsThe table below gives data points for the continuous function y f x 0 2 4 6 8 1 0 1 2 1 4 1 6 1 8 2 0 f x 30 44 55 68 66 54 39 37 26 25 40 X Approximate the area under the curve y f x on the interval 0 2 using left hand endpoints and 10 equal subdivisions You get Area OA 88 8 OB 454 OC 90 8 OD 96 8 OE 444

Calculus
Vector CalculusThe function y 55 0 3 graphed below S Which of the following Riemann sums yields the exact area under the curve on the interval 0 6 O A R 1 f wk Ack where the subdivisions are taken to be at 0 2 3 4 6 and right hand endpoints are used and R E 1f w Axk where the subdivisions are taken to be at 0 2 3 4 6 and midpoints are used O B R f wk Axk where the subdivisions are taken to be at 0 2 3 4 6 and midpoints are used O c R f wk A k where the subdivisions are taken to be at 0 2 3 4 6 and right hand endpoints are used O D R f w A k where 6 equal subdivisions and right hand endpoints are used O E R f wk Ak where 6 equal subdivisions and left hand endpoints are used
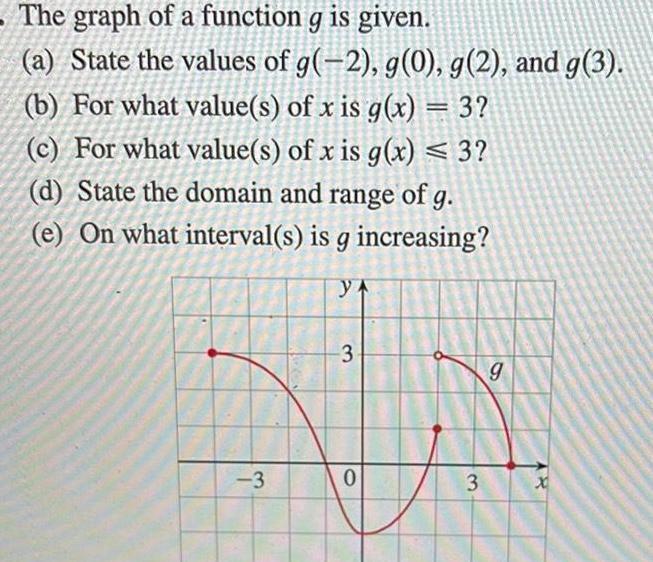
Calculus
Limits & ContinuityThe graph of a function g is given a State the values of g 2 g 0 g 2 and g 3 b For what value s of x is g x 3 c For what value s of x is g x 3 d State the domain and range of g e On what interval s is g increasing YA 3 3 0 3 9 x

Calculus
Application of derivativesSolve each of the linear systems in Problems 13 through 20 to determine whether the critical point 0 0 is stable asymptot cally stable or unstable Use a computer system or graphing calculator to construct a phase portrait and direction field for the given system Thereby ascertain the stability or instabil ity of each critical point and identify it visually as a node a saddle point a center or a spiral point 15 dx dt 2x dy dt y
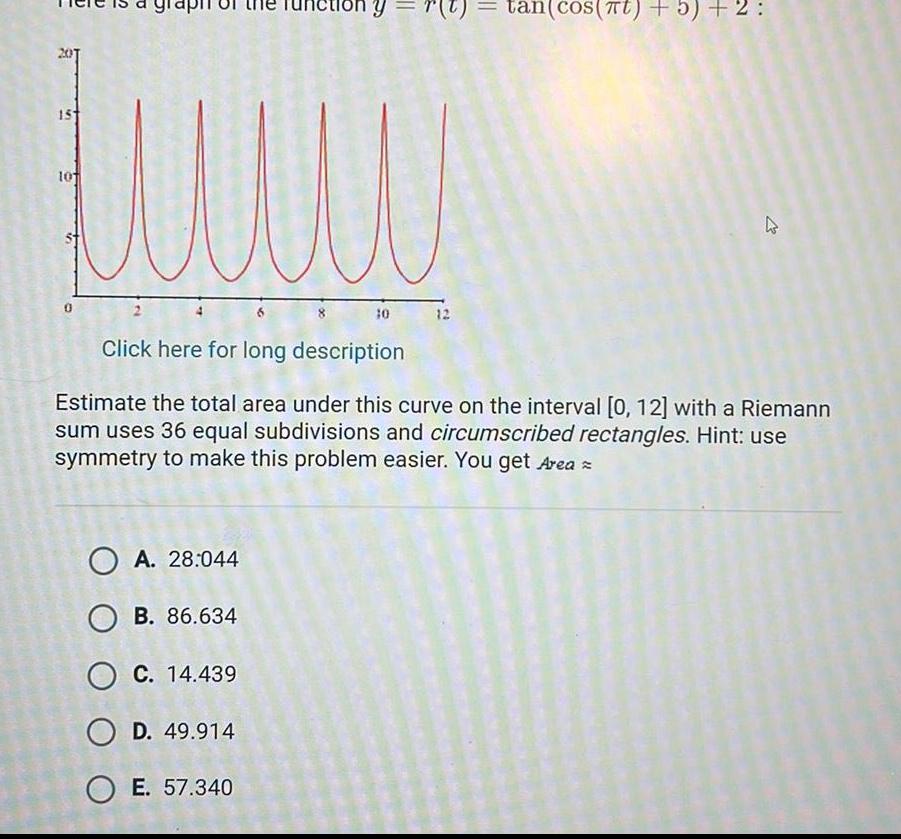
Calculus
Application of derivatives15 10 ny OA 28 044 OB 86 634 O C 14 439 OD 49 914 OE 57 340 10 12 tan cOS TU 3 2 27 Click here for long description Estimate the total area under this curve on the interval 0 12 with a Riemann sum uses 36 equal subdivisions and circumscribed rectangles Hint use symmetry to make this problem easier You get Area

Calculus
Application of derivatives1 The U S Post Office will accept a box for shipment only if the sum of the length and girth distance around is at most 108 inches Find the dimensions of the largest acceptable box with square ends air cargo fragile

Calculus
Application of derivativesYou re sunbathing on the island shown on the map below The island is six miles from shore at the closest point and the nearest store is a convenience store seven miles down the beach If you can row at 4 miles an hour and you can walk at 5 miles an hour where should you land to get a bag of tortilla chips in the least possible time Ignore tides currents and sharks No fair renting a helicopter a 7 miles

Calculus
Vector CalculusThe ellipse x 3y2 13 below has two points when x 1 m 2 7 O T 28 1 Find the slope of the ellipse at both these points I 2 Thoroughly explain the method you used to find the slope in part 1 What are the strength and weaknesses of the method you used 3 Explain whether your method will work to find the slope of x2 xy y2 3 at points 1 2 ar 1 1 If it succeeds please show your work as you find these two slopes If your method fai that s fine just explain thoroughly why it failed

Calculus
Differentiation3 Find the point on the graph of y x2 1 that s closest to the point 8 1 5 Hint Remember the distance formula The distance between two points in a plane is d x x 12 2 2

Calculus
Application of derivatives4 Given a right circular cone you put an upside down cone inside it so that its vertex is at the center of the base of the larger cone and its base is parallel to the base of the larger cone If you choose the upside down cone to have the largest possible volume what fraction of the volume of the larger cone does it occupy Let H and R be the height and radius of the large cone let h and be the height and radius of the small cone Use similar triangles to get an equation relating and r The formula for the volume of a cone is V r h

Calculus
Definite Integrals2 A rectangular piece of cardboard 8 inches by 14 inches is used to make an open top box by cutting out a small square from each corner and bending up the sides What size square should be cut from each corner for the box to have the maximum volume 8 14

Calculus
Vector Calculus1 Below is a chart that gives some information regarding a twice differentiable function fx The n a in the chart means not applicable x 4 x 4 4 x 0 x 0 0 x 4 x 4 4 x n a n a 1 n a 5 n a negative 0 positive 0 negative 0 positive n a f x x Concavity 3 n a n a Fill in the last row of the chart the four empty spaces with the proper concavity either concave up or concave down and then sketch a graph that satisfies all the conditions in the chart

Calculus
Differential equationsA Suppose the height of an object at any time 20 is given by the function h t where his feet and is in seconds The first derivative h t represents the rate of change in height with respect to time which is actually the velocity of the object and the units are feet per second What does the second derivative h t represent and what are the units B Suppose the population of a bacteria culture is given by the function p t where is population in thousands and represents time in hours Then p t represents the rate of change in the population of the bacteria with respect to time and its units are in thousands of bacteria per hour What does p t represent and what are its units C Suppose that 7 t is a twice differentiable function of 1 where T is in C and is in minutes What are the units of T t and T t
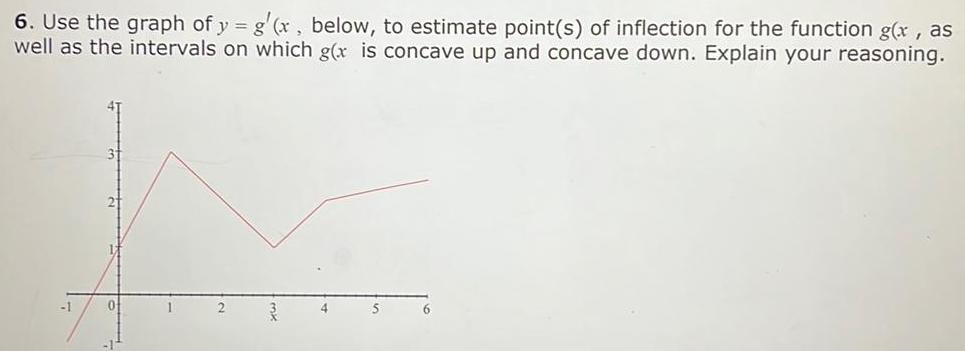
Calculus
Differentiation6 Use the graph of y g x below to estimate point s of inflection for the function g x as well as the intervals on which g x is concave up and concave down Explain your reasoning 1 6

Calculus
Indefinite Integration2 For each of the functions below use your graphing calculator to draw a graph of the function and then estimate the x coordinates of its inflection points List all estimated points of inflection all intervals where the function is concave up and all the intervals where the function is concave down You don t need to show your graphs and of course your estimates don t have to be perfect A f x xe B f x tanx on the domain x C f x 1

Calculus
Limits & Continuity7 Suppose you know that f x is an odd function on the domain of all real numbers and that th function is concave up on the intervals 0 x 3 and 5 x and concave down on the interval 3 x 5 List ALL intervals on which the function fx is concave up and ALL intervals on which the function fx is concave down explain how you know these to be correct

Calculus
Differentiation3 Consider the function f x 2x 3x 6 x 2 A Find f x Show your work B Graph f x on your calculator and use this graph to answer the following questions On what interval s is f x concave up and how did you use the graph of f x to estimate On what interval s is f x concave down and how did you use the graph of f x to estima this Note You don t need to include a sketch of y f x in your answer

Calculus
Differential equations4 Consider the function x x x 3 x2 As in the last problem find f x showing all work and use the graph of this function to estimate where fx is concave up and where fx is concave down You don t need to include sketch of the graph of f x in your answer

Calculus
Limits & Continuity2 Consider the function f x x x Use graphical methods to discuss the differentiability of the function In particular find all values of x for which the function appears non differentiable and explain why Include at least one graph illustrating each point of non differentiability

Calculus
Vector CalculusFind a power series solution of the form y x 0 Cnx of the given differential equation x y y 0 First compute y x Use cn for c in your answer Then x y x y Co C1 Cn n 1 Use c0 for co c1 for c cn for c and cnm1 for C 1 in your answer Requiring that the terms of this series for x y y vanish gives X7 1 Cn 1 for n 2 100 x 2 The series solution converges to the familiar function y f x x