Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
Vector Calculus7 a Find the arc length parametrization of the curve that is the intersection of the elliptic cylinder y 1 and the plane z 2y 7 5 Use s as the arc length parameter with s 0 corresponding to the point 0 1 9 oriented counter clockwise as seen from above Also if the density is given by 8 x y z z set up an expression for its mass
Calculus
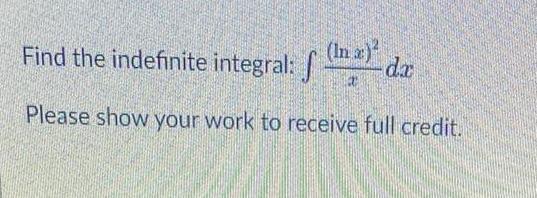
Indefinite IntegrationFind the indefinite integral f x da Please show your work to receive full credit

Calculus
DifferentiationTo find the derivative of the function f x sqrt 3 x 2 we can apply the power rule for differentiation
Calculus
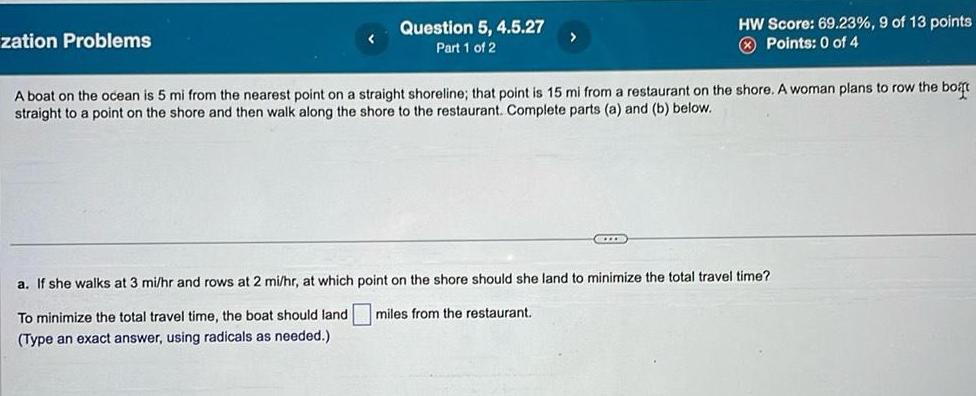
Application of derivativeszation Problems Question 5 4 5 27 Part 1 of 2 HW Score 69 23 9 of 13 points Points 0 of 4 A boat on the ocean is 5 mi from the nearest point on a straight shoreline that point is 15 mi from a restaurant on the shore A woman plans to row the boat straight to a point on the shore and then walk along the shore to the restaurant Complete parts a and b below COLLE a If she walks at 3 mi hr and rows at 2 mi hr at which point on the shore should she land to minimize the total travel time miles from the restaurant To minimize the total travel time the boat should land Type an exact answer using radicals as needed
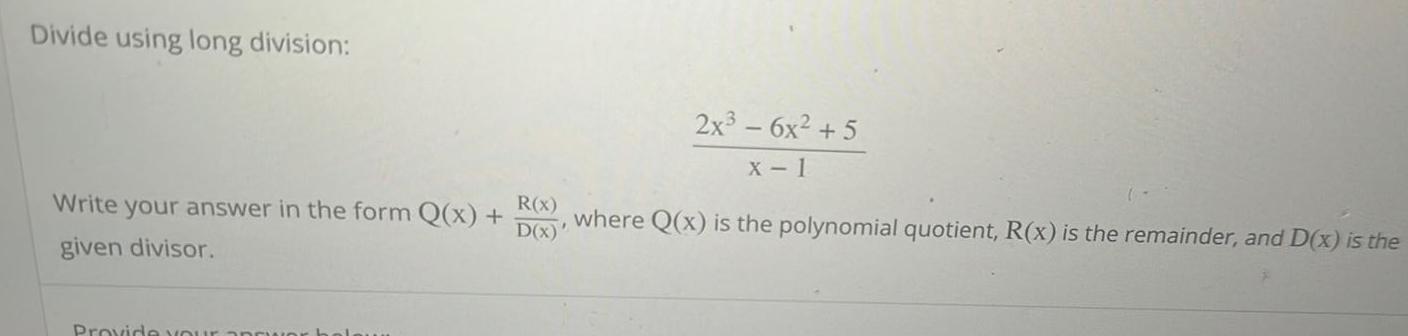
Calculus
Limits & ContinuityDivide using long division Write your answer in the form Q x given divisor Provide your R x D x 2x 6x 5 X 1 where Q x is the polynomial quotient R x is the remainder and D x is the

Calculus
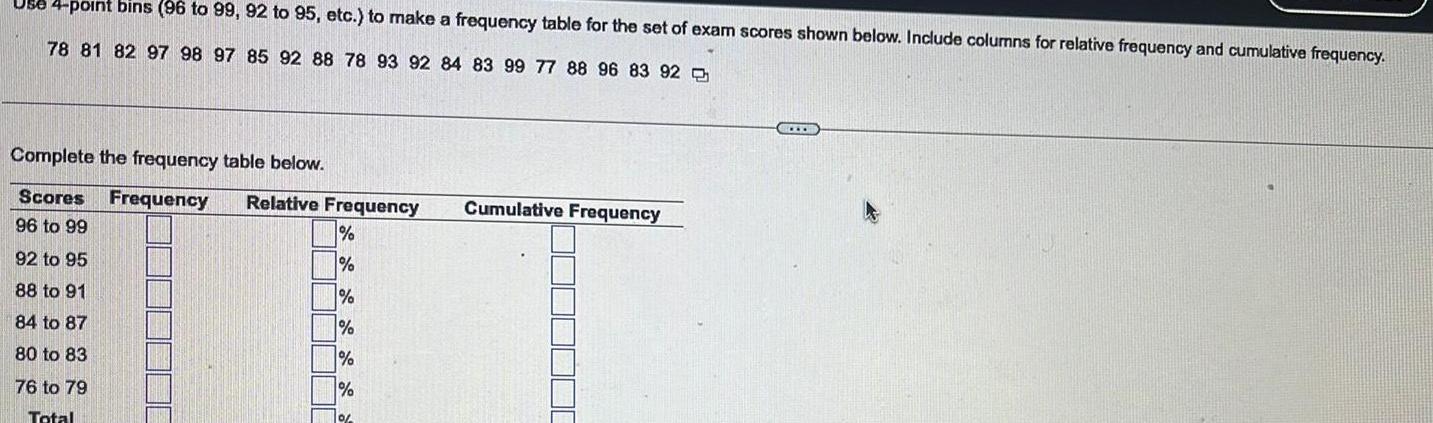
Vector Calculus4 point bins 96 to 99 92 to 95 etc to make a frequency table for the set of exam scores shown below Include columns for relative frequency and cumulative frequency 78 81 82 97 98 97 85 92 88 78 93 92 84 83 99 77 88 96 83 92 Complete the frequency table below Scores Frequency 96 to 99 92 to 95 88 to 91 84 to 87 80 to 83 76 to 79 Total Relative Frequency 7 Cumulative Frequency ww

Calculus
Application of derivativesAn archer releases an arrow with an initial velocity of 30 feet per second at a height of 3 feet The patffthe arrow takes can be modeled using the function f x 16x 30x 3 where f x represents the height in feet of the arrow and x represents the time the arrow travels in seconds How many seconds until the arrow hits the ground Round your answer to the nearest hundredth if necessary Do not include units in your answer Drouide
Calculus
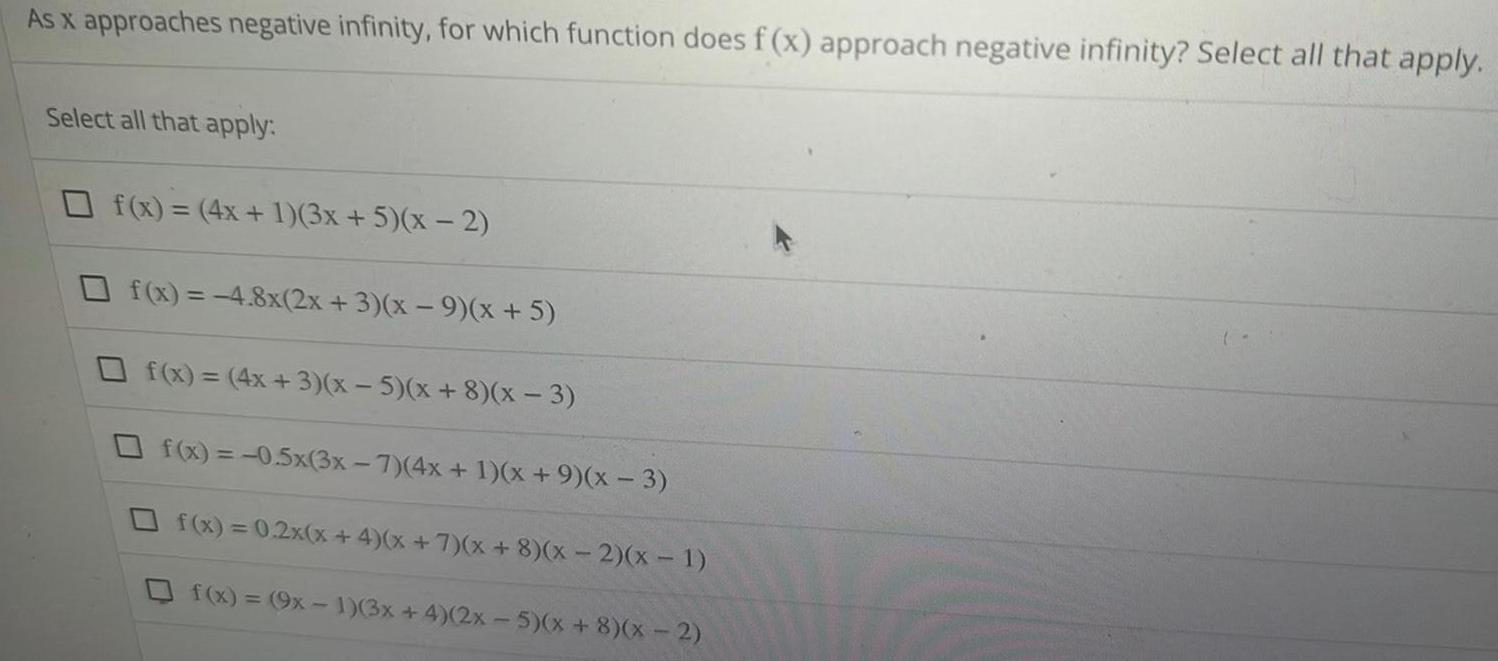
Application of derivativesAs x approaches negative infinity for which function does f x approach negative infinity Select all that apply Select all that apply f x 4x 1 3x 5 x 2 f x 4 8x 2x 3 x 9 x 5 f x 4x 3 x 5 x 8 x 3 f x 0 5x 3x 7 4x 1 x 9 x 3 f x 0 2x x 4 x 7 x 8 x 2 x 1 f x 9x 1 3x 4 2x 5 x 8 x 2

Calculus
Application of derivativesQuestion The flight of a kicked football follows the quadratic function f x 0 02x 2 2x 2 where f x is the vertical dista in feet and x is the horizontal distance the ball travels How far in feet will the ball travel across the field by the time it F the ground Round your answer to one decimal place Provide your answer below
Calculus
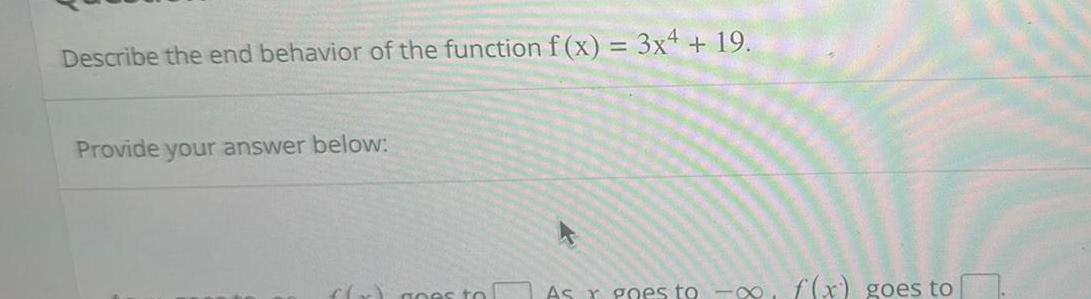
Application of derivativesDescribe the end behavior of the function f x 3x4 19 Provide your answer below f x goes to As r goes to f x goes to

Calculus
Differential equationsA model rocket is launched directly upward at a speed of 20 meters per second from the ground The function f t 4 91 20t models the relationship between the height of the rocket and the time after launch t in seconds When in seconds after launch will the rocket reach its highest point Round to two decimal places Provide your answer below seconds

Calculus
Definite IntegralsThe function h t 16t 48t 28 models the height in feet of a ball where t is the time in seconds What is the maximum height that the ball reaches Just write the numerical answer do not include h or any units in your answer
Calculus
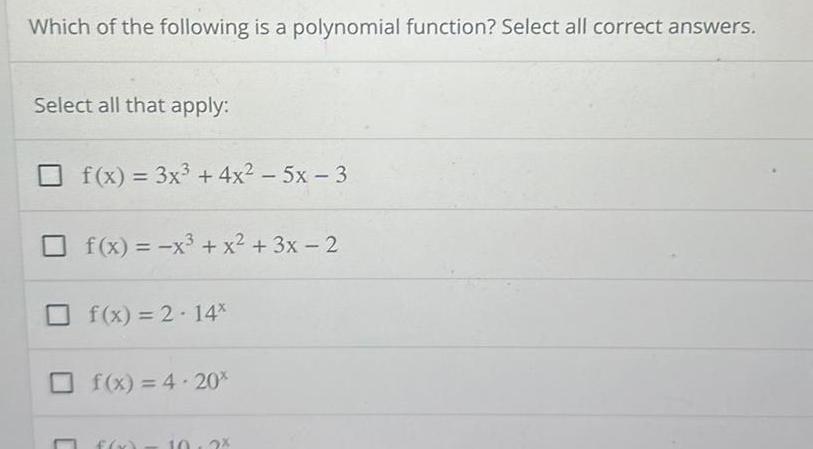
Application of derivativesWhich of the following is a polynomial function Select all correct answers Select all that apply f x 3x 4x 5x 3 f x x x 3x 2 f x 2 14 f x 4 20 2

Calculus
Application of derivativesA ball is launched directly in the air at a speed of 40 feet per second from a platform located 10 feet in the air The motion of the ball can be modeled using the function f t 16t 40t 10 where t is the time in seconds and f t is the heig of the ball When in seconds will the ball hit the ground Write your answer to the nearest hundredth of a second Do not include units in your answer Provide your answer below

Calculus
Definite IntegralsFind the y intercept of the following function f x x 13x 42 Write your answer in the form x y and use fractions if necessary
Calculus
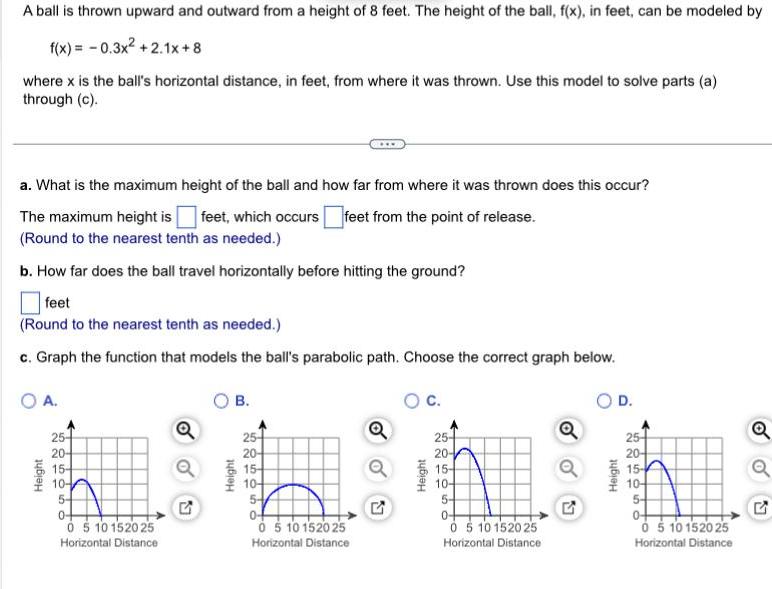
Application of derivativesA ball is thrown upward and outward from a height of 8 feet The height of the ball f x in feet can be modeled by f x 0 3x 2 1x 8 where x is the ball s horizontal distance in feet from where it was thrown Use this model to solve parts a through c a What is the maximum height of the ball and how far from where it was thrown does this occur The maximum height is feet which occurs feet from the point of release Round to the nearest tenth as needed b How far does the ball travel horizontally before hitting the ground feet Round to the nearest tenth as needed c Graph the function that models the ball s parabolic path Choose the correct graph below O A Height 25 20 15 10 5 0 0 5 10 152025 Horizontal Distance Q G B Height 25 20 15 10 5 0 0 5 10 15 20 25 Horizontal Distance oo G C Height 25 20 15 104 5 04 0 5 10 152025 Horizontal Distance Q D Height 25 20 15 104 5 0 0 5 10 15 20 25 Horizontal Distance Q Q
Calculus
Definite IntegralsA company is planning to manufacture mountain bikes The fixed monthly cost will be 300 000 and it will cost to produce each bicycle SIXX A Write the cost function C of producing x mountain bikes per month C x B Write the average cost function C of producing x mountain bikes per month C x C Find and interpret C 500 C 1000 C 2000 and C 4000 C 500 Interpret C 500 When bicycles are produced in a month it costs C 1000 Interpret 1000 When bicycles are produced in a month it costs C 2000 Interpret C 2000 When bicycles are produced in a month it costs to produce each bicycle to produce each bicycle to produce each bicycle C 4000 Interpret C 4000 When bicycles are produced in a month it costs to produce each bicycle D What is the horizontal asymptote for the graph of the average cost function C The horizontal asympote is Type an equation Describe what this means in practical terms O A When 300 000 bicycles are produced in a month the cost per bicycle is at a minimum OB When 200 bicycles are produced in a month the cost per bicycle is at a minimum OC The cost per bicycle approaches 200 as more bicycles are produced in a month OD The cost per bicycle approaches 300 000 as more bicycles are produced in a month
Calculus
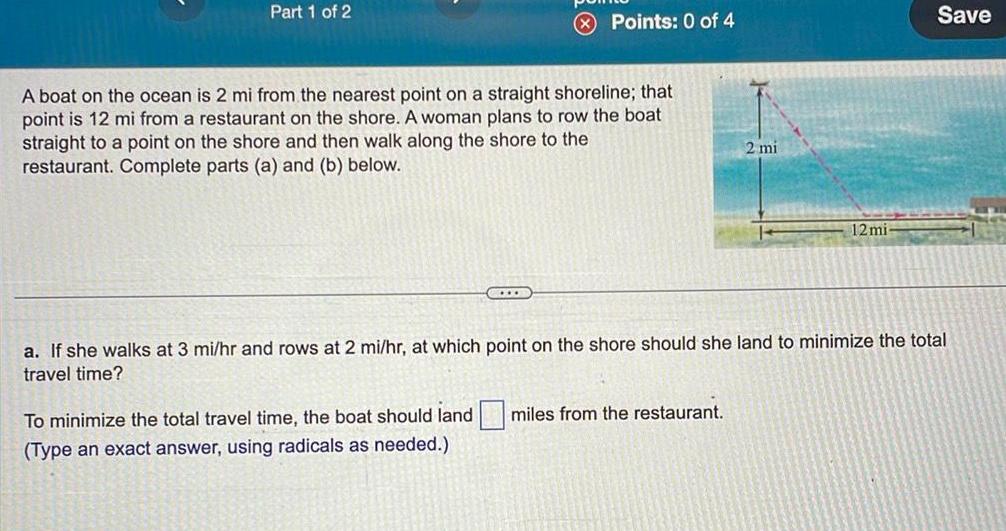
Vector CalculusPart 1 of 2 Points 0 of 4 A boat on the ocean is 2 mi from the nearest point on a straight shoreline that point is 12 mi from a restaurant on the shore A woman plans to row the boat straight to a point on the shore and then walk along the shore to the restaurant Complete parts a and b below COLLE 2 mi To minimize the total travel time the boat should land miles from the restaurant Type an exact answer using radicals as needed 12 mi Save a If she walks at 3 mi hr and rows at 2 mi hr at which point on the shore should she land to minimize the total travel time
Calculus
Vector CalculusPart 2 of 2 a Squares with sides of length x are cut out of each corner of a rectangular piece of cardboard measuring 7 ft by 5 ft The resulting piece of cardboard is then folded into a box without a lid Find the volume of the largest box that can be formed in this way Points 0 of 1 b Suppose that in part a the original piece of cardboard is a square with sides of length s Find the volume of the largest box that can be formed in this way C a The maximum volume of the box is approximately 15 02 ft Round to the nearest hundredth as needed b The maximum volume of the box is Type an expression using s as the variable Save

Calculus
Vector CalculusThe electric current i in mA in the circuit i 7 4 1 e 0 42t where t is the time in s Evaluate i for t 9 0 m i mA Round to four decimal places as needed
Calculus
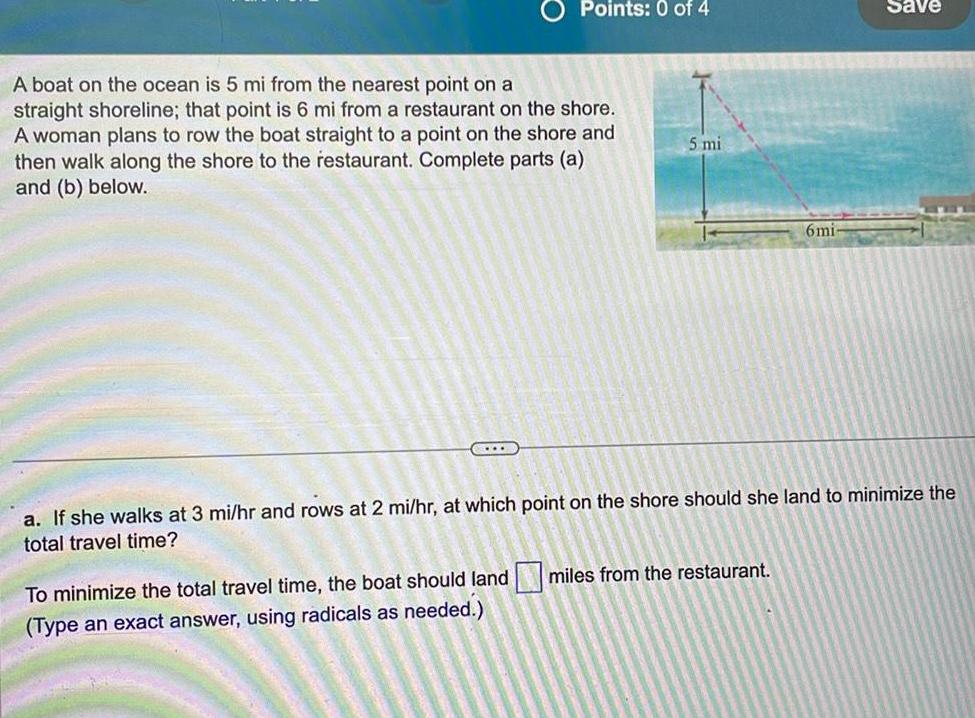
Application of derivativesPoints 0 of 4 A boat on the ocean is 5 mi from the nearest point on a straight shoreline that point is 6 mi from a restaurant on the shore A woman plans to row the boat straight to a point on the shore and then walk along the shore to the restaurant Complete parts a and b below 5 mi 6mi To minimize the total travel time the boat should land miles from the restaurant Type an exact answer using radicals as needed Save a If she walks at 3 mi hr and rows at 2 mi hr at which point on the shore should she land to minimize the total travel time
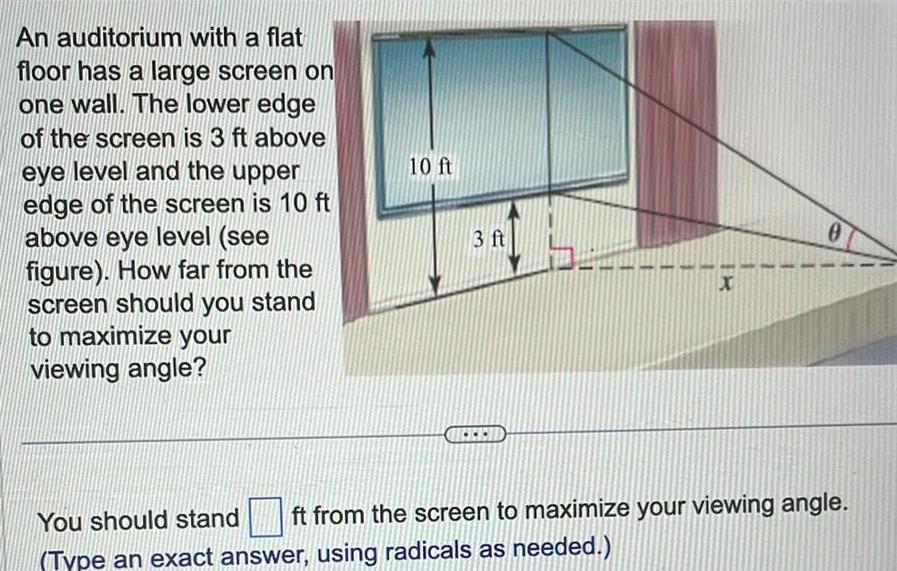
Calculus
Application of derivativesAn auditorium with a flat floor has a large screen on one wall The lower edge of the screen is 3 ft above eye level and the upper edge of the screen is 10 ft above eye level see figure How far from the screen should you stand to maximize your viewing angle 10 ft 3 ft X 0 You should stand ft from the screen to maximize your viewing angle Type an exact answer using radicals as needed
Calculus
Application of derivativesA rectangular tank with a square base an open top and a volume of 10 976 ft is to be constructed of sheet steel Find the dimensions of the tank that has the minimum surface area The tank with the minimum surface area has a height of with a side length of ft ft and a square base
Calculus
Application of derivativesa Squares with sides of length x are cut out of each corner of a rectangular piece of cardboard measuring 7 ft by 5 ft The resulting piece of cardboard is then folded into a box without a lid Find the volume of the largest box that can be formed in this way b Suppose that in part a the original piece of cardboard is a square with sides of length s Find the volume of the largest box that can be formed in this way a The maximum volume of the box is approximately Round to the nearest hundredth as needed ft
Calculus
Definite IntegralsA rectangle is constructed with its base on the x axis and its upper two vertices on the parabola y 25 x What are the dimensions of the rectangle with the maximum area What is the area THEONE and the longer The shorter dimension of the rectangle is dimension is Type an exact answer using radicals as needed
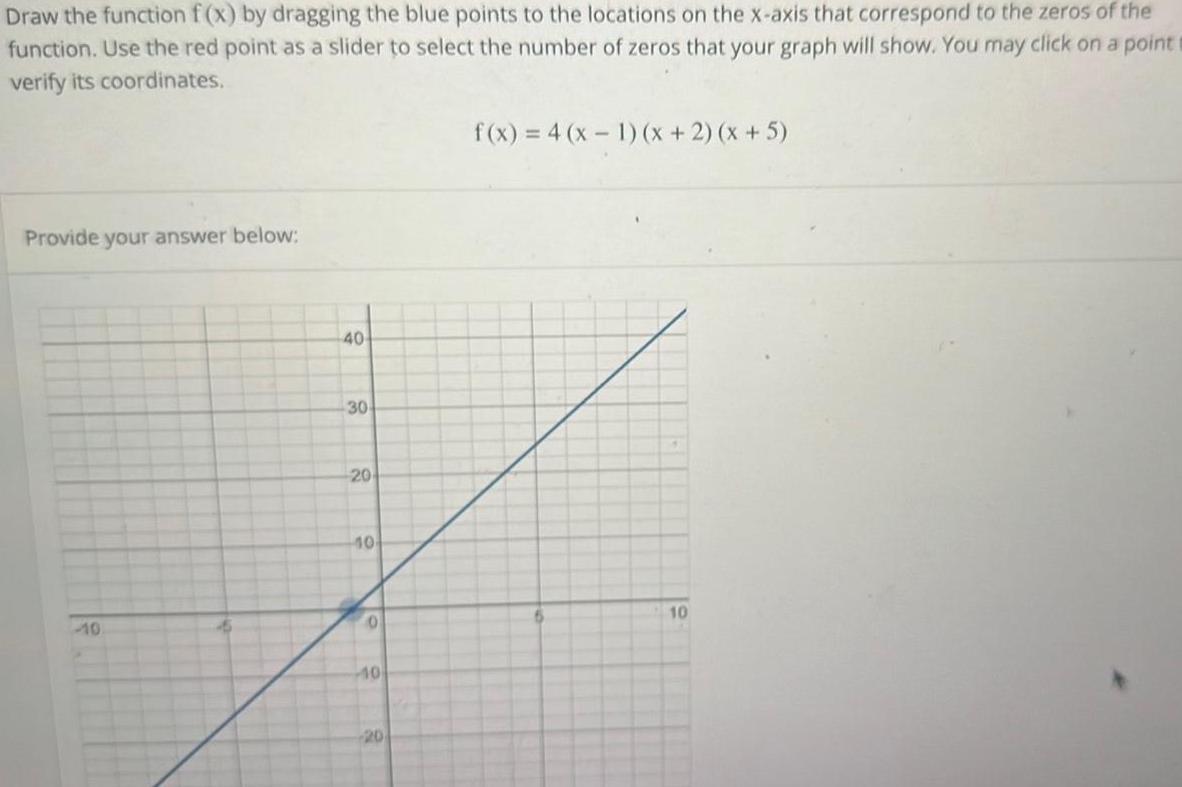
Calculus
Application of derivativesthe Draw the function f x by dragging the blue points to the locations on the x axis that correspond to the zeros of function Use the red point as a slider to select the number of zeros that your graph will show You may click on a point verify its coordinates Provide your answer below 40 30 20 10 0 10 20 f x 4 x 1 x 2 x 5 10

Calculus
Application of derivativesA single card is selected from an ordinary deck of cards The sample space is shown below Find the probabilities Enter the probabilities as fractions a 1 4 47 ND P club and a king b P club or a king 200 Hearts red cards Diamonds red cards 44 N Spades black cards Clubs black cards

Calculus
Differential equations56 Points DETAILS SMITHNM13 13 3 025 ppose that the odds in favor are 16 to 1 that a man will be bald by the time he is 60 State this as a probability Enter the probability as a ction man is bald by 60
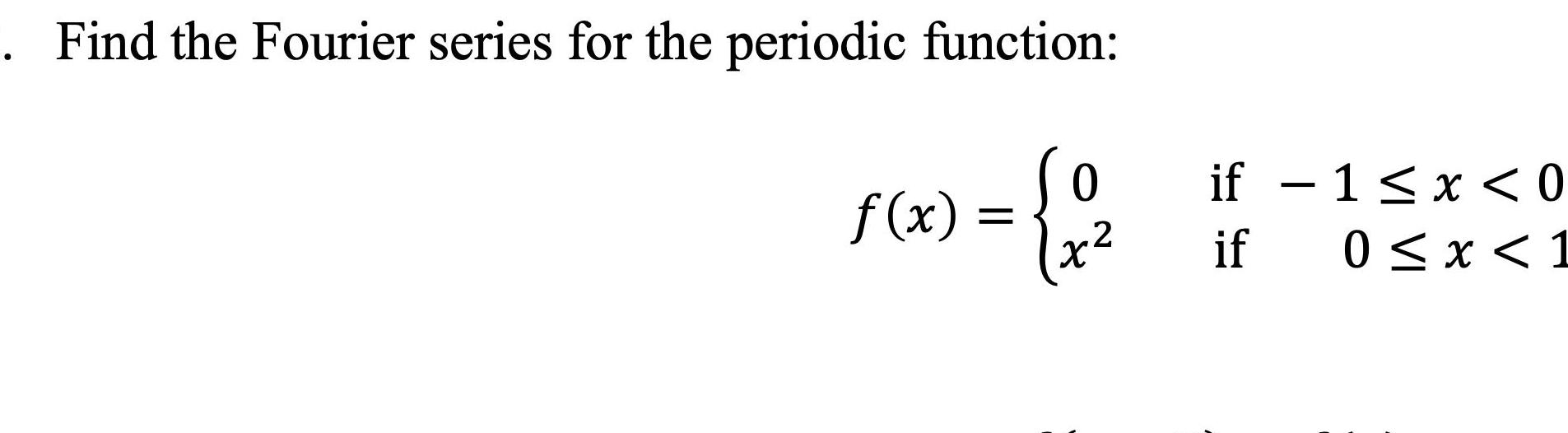
Calculus
Indefinite IntegrationFind the Fourier series for the periodic function x 0 2 x if 1 x 0 if 0 x 1

Calculus
Application of derivativesConsider the ollowing table showing the results of a survey of TV network executives Opinion of Current Programming Network Satisfied S Not Satisfied S Total 18 30 22 35 15 30 95 NBC N CBS C ABC A Total 55 2259 12 13 15 40 uppose one network executive is selected at random Find the indicated probabilities Round your answers to four decimal places a What is the probability that it is an NBC executive b What is the probability that the selected person is satisfied c What is the probability the selected person is from CBS if we know the person is satisfied with current programming d What is the probability the selected person is satisfied if we know the person is from CBS

Calculus
Limits & ContinuityFind the measure of the least positive angle that is coterminal with the angle given Then find the measure of the negative angle that is nearest to and is coterminal with the angle given 51 The positive angle is

Calculus
Definite IntegralsIf a region is bounded by y lnx x 0 y 2 and y 1 find the definite integral that will compute for the moment with respect to y axis

Calculus
Definite IntegralsConsider the parametric equations below x sin t y sin 4t Osts 2 Set up an integral that represents the area of the surface obtained by rotating the given curve about the x a C at dt Use your calculator to find the surface area correct to four decimal places

Calculus
Differential equations1 point Convert the nonhomogeneous differential equation y 3y 7y 1 to a first order system Let x y x y Enter x and x in your answers as x1 and x2 x t x t help formulas help formulas
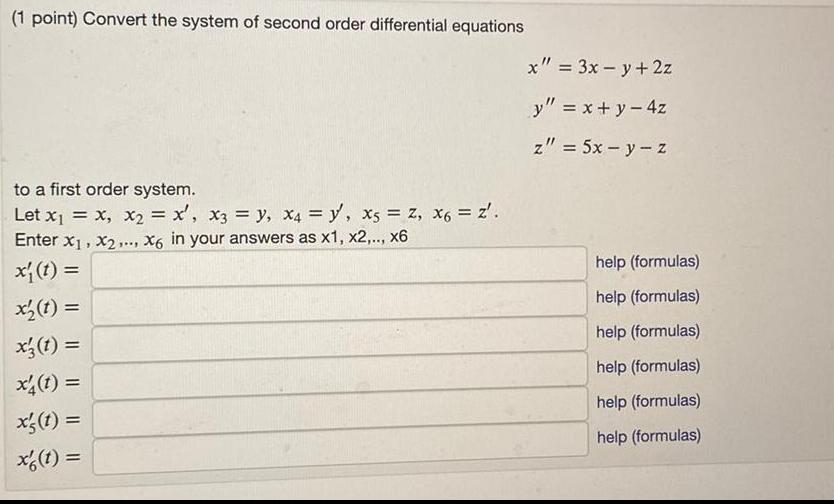
Calculus
Differential equations1 point Convert the system of second order differential equations to a first order system Let x x x x x3 y x4 y x5 Z x6 Z Enter x x2 X6 in your answers as x1 x2 x6 x t x t x t x4 1 x s t x t x 3x y 2z y x y 4z z 5x y z help formulas help formulas help formulas help formulas help formulas help formulas
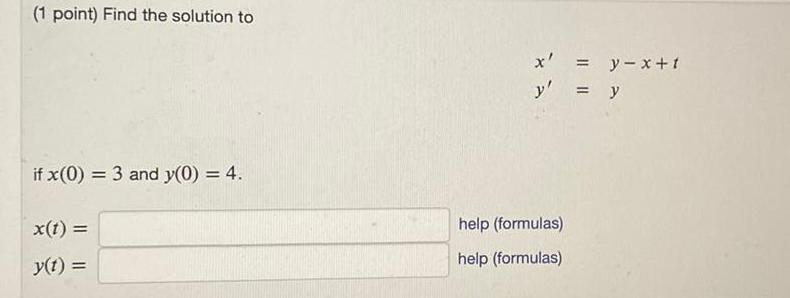
Calculus
Differential equations1 point Find the solution to if x 0 3 and y 0 4 x t y t x y x t y y help formulas help formulas

Calculus
Vector Calculus1 point Consider the second order differential equation with initial conditions Without solving it rewrite the differential equation as an equivalent set of first order equations In your answer use the single letter u to represent the function u and the single letter v to represent the velocity function u Do not use u t or u t to represent these functions Expressions like sin t that represent other functions are OK u U Now write the first order system using matrices d dt u V u 6 5u 3u 1 5 sin 31 u 1 6 u 1 4 5 The initial value of the vector valued solution for this system is u 1 v 1 BIO E

Calculus
Vector Calculus1 point This is the second part of a two part problem Show that y t is a solution to the system of linear homogeneous differential equations y y y3 y y 2y2 y3 et a Find the value of each term in the equation y 2y y2 y3 in terms of the variable 1 Enter the terms in the order given 2y y2 Y3 1 y2 2y3 b Find the value of each term in the equation y2 y y2 2y3 in terms of the variablet Enter the terms in the order given c Find the value of each term in the equation y y 2y2 y3 in terms of the variablet Enter the terms in the order given

Calculus
Differential equations1 point Consider the system of differential equations Verify that 3 0 X 1 e 1 is a solution to the system of differential equations for any choice of the constants c and c2 Find values of c and c that solve the given initial valu problem According to the uniqueness theorem you have found the unique solution of x Px x 0 o t DH e4r

Calculus
DifferentiationLet part of a two part problem P 8 6 cos 61 sin 6t Enter your answers in terms of the variable t x 0 13 a Show that x 1 is a solution to the system Px by evaluating derivatives and the matrix product 06 86 6 Enter your answers in terms of the variablet 6 sin 6t 6 cos 6t x 1 6 b Show that x 1 is a solution to the system Px by evaluating derivatives and the matrix product 06 31 1 6 X 1

Calculus
Vector Calculus1 point This is the second part of a two part problem Let 7 1 sin 6 cos 61 Compute the wronskian to determine whether the functions x 1 and x t are linearly independent Wronskian det x 1 6 sin 6t 6 cos 61

Calculus
Differential equationspoint This is the first part of a two part problem ewrite the given system of linear homogeneous differential equations as a homogeneous linear system of the form y Py y 2y1 y2 Y3 y y2 2y3 1 y 2y2 y3 Y Y1 3 2 Va
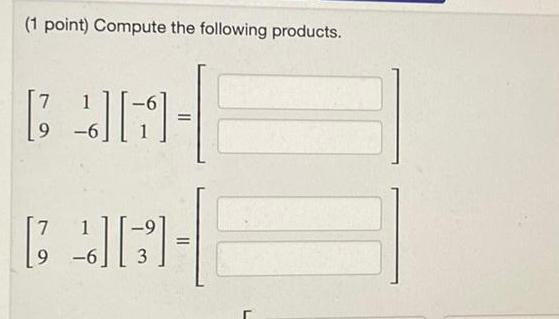
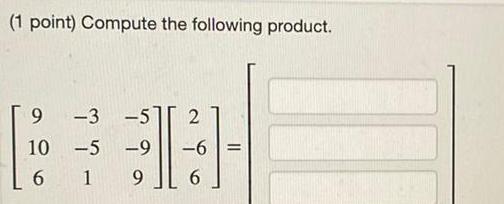
Calculus
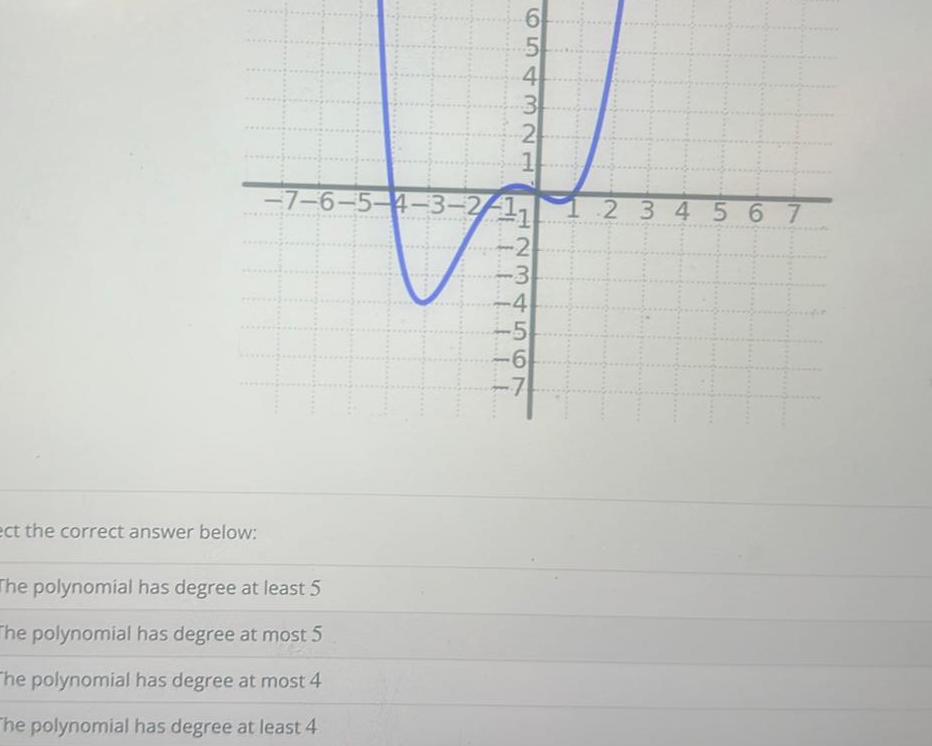
Application of derivativesect the correct answer below The polynomial has degree at least 5 The polynomial has degree at most 5 The polynomial has degree at most 4 The polynomial has degree at least 4 6 5 LLI 4 4321 7 6 5 4 3 2 1 11 2 3 4567AWNH 4 5 6 7 2 3 4 567
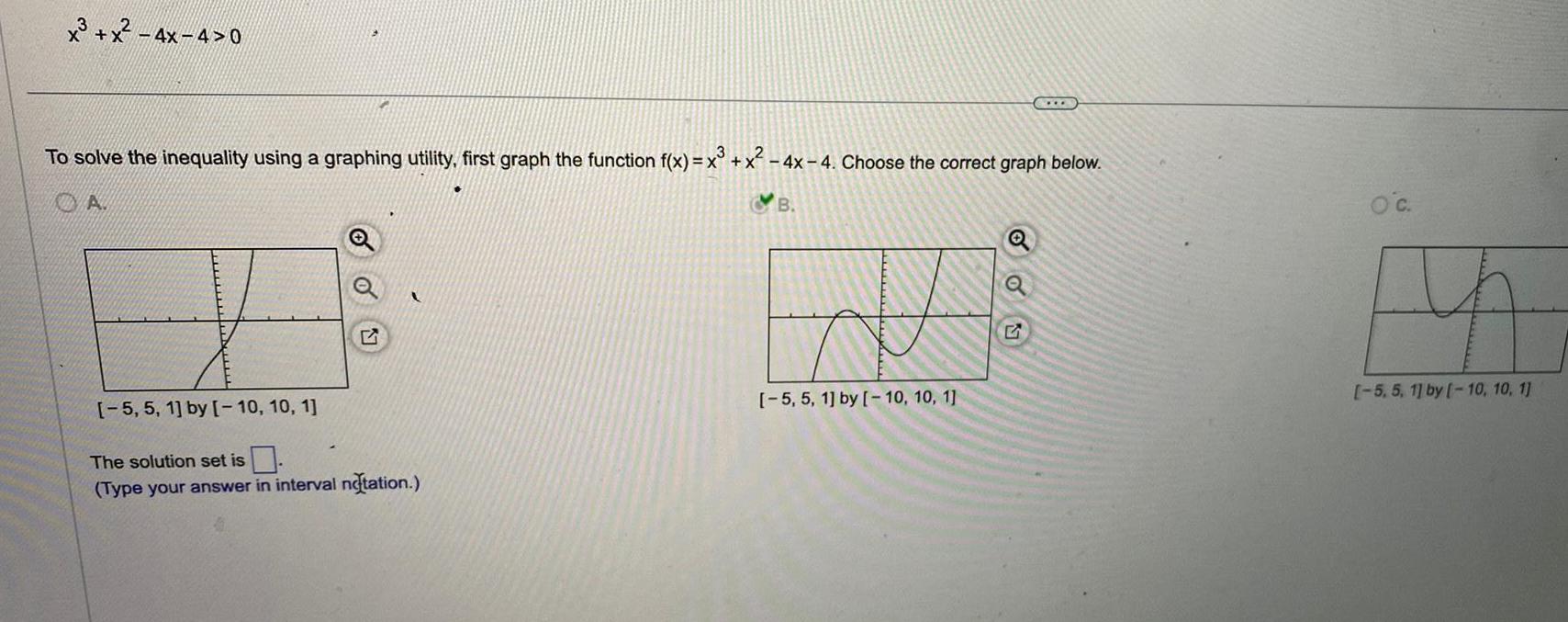
Calculus
Application of derivativesx x 4x 4 0 3 To solve the inequality using a graphing utility first graph the function f x x x 4x 4 Choose the correct graph below A B 5 5 1 by 10 10 1 E The solution set is Type your answer in interval notation 5 5 1 by 10 10 1 Q OU OC 5 5 1 by 10 10 1
Calculus
Limits & ContinuityWhich is an equation with a degree of 3 x intercepts located at 3 0 and 2 0 and a y intercept located at 0 0 Select the correct answer below O y x x 3 x 2 O y x x 3 x 2 Oy x 3 x 2 Oy x 3 x 2 Oy x 2 x 3
Calculus
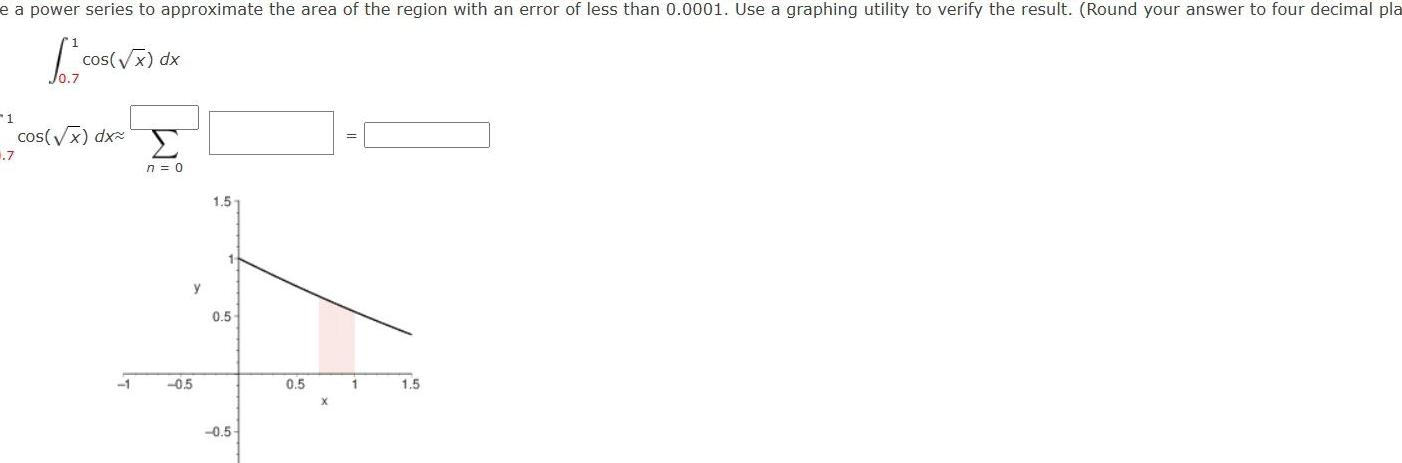
Limits & Continuitye a power series to approximate the area of the region with an error of less than 0 0001 Use a graphing utility to verify the result Round your answer to four decimal pla cos x dx 1 1 7 cos x dx 1 n 0 y 0 5 1 5 1 0 5 0 5 0 5 1 1 5

Calculus
Definite IntegralsThe table provides various values including select minimums and maximums of a particular cosine function f x Angle T negative 3 times pi over 4 negative pi over 2 negative pi over 4 0 pi over 2 f x 2 1 4 1 2 4 2 What is the period of the function that contains these points