Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
Vector CalculusConsider the function f x x 3 6x 2 9x 1 a Find the critical points of f x and determine whether each point is a la maximum local minimum or neither b Determine the intervals where f x is increasing or decreasing c Find the points of inflection of f x and determine whether each pa corresponds to a concave up or concave down region

Calculus
Vector CalculusFind a polar equation for the parabola with focus 0 0 and directrix r cos 0 2 2

Calculus
Differential equationsFind the domain and range of the given function and identify its level curves Sketch a typical level 2 f x y qx y curve

Calculus
Differential equationsEvaluate fzyldz y dz 2 dy where C is the rectangle with vertices 0 0 4 0 4 1 and 0 1

Calculus
Differential equations1 point Determine the bifurcation value s for the one parameter family k help numbers dy dt Determine which differential equation corresponds to each phase line You should be able to state briefly how you know your choices are correct 1 K equal to the bifurcation value 2 k larger than the bifurcation value 3 K smaller than the bifurcation value y k A B

Calculus
Application of derivativesConsider the autonomous differential equation Critical Point 1 Critical Point 2 Critical Point 3 Use a computer system of graphics calculator to plot a slope field and or enough solution curves to indicate the stability or instability of each critical point of the differential equation Some of these critical points may be semistable List the critical points in increasing order is is is dx dt x x 4

Calculus
Indefinite IntegrationProblem 4 20pts Use the Divergence Theorem to evaluate the following Surface Integral fr where the vector field F is given by F dS F 2x 2 i x y j xz k and the closed surface S is given by the unit cube where the coordinates x y and z take values from 1to1 raspectively

Calculus
Application of derivativesdy Let y t be the solution to d 7te satisfying y 0 3 dt a Use Euler s Method with time step h 0 2 to approximate y 0 2 y 0 4 y 1 0 ktk 00 10 2 20 4 30 6 40 8 51 0 Yk 3 b Use separation of variables to find y t exactly y t c Compute the error in the approximations to y 0 2 y 0 6 and y 1 y 0 2 Y y 0 6 Y3 ly 1 ys

Calculus
Application of derivativesdy Let y t be the solution to dr y satisfying y 0 2 dt Use Euler s Method with time step h 0 2 to approximate y 0 2 y 0 4 y 1 0 f tn yn Ay ntn 00 10 2 20 4 30 6 40 8 51 0 Yn 2 h 0 2 0 2 0 2 0 2 0 2
Calculus
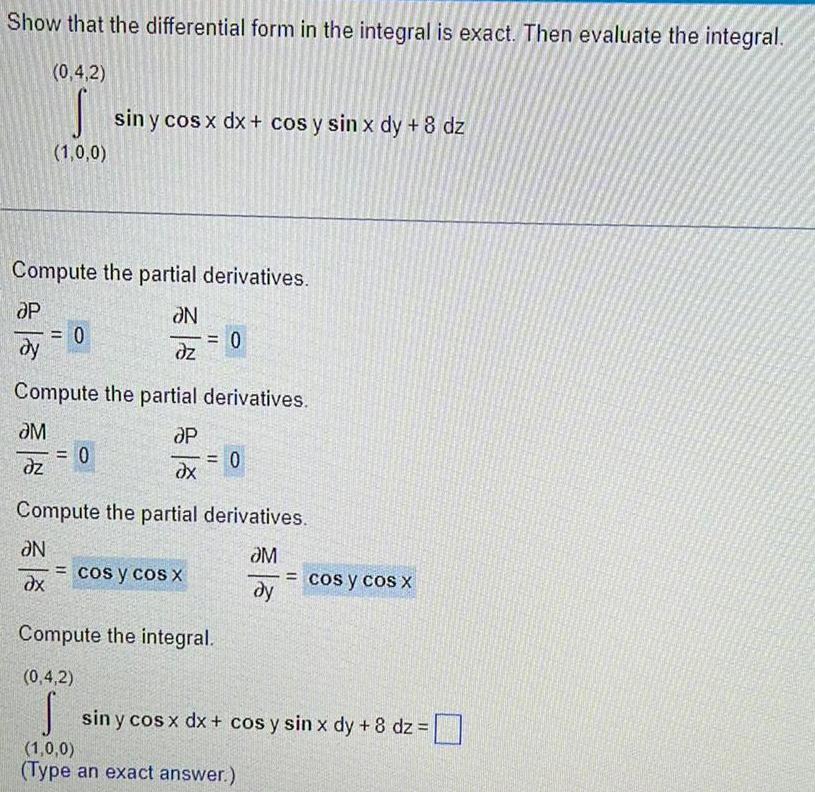
Vector CalculusShow that the differential form in the integral is exact Then evaluate the integral 0 4 2 S 1 0 0 Compute the partial derivatives OP N dy dz 0 sin y cos x dx cos y sin x dy 8 dz N ax Compute the partial derivatives M P dz dx 0 0 Compute the partial derivatives M dy cos y cos X 0 Compute the integral 0 4 2 S 1 0 0 Type an exact answer cos y cos x sin y cos x dx cos y sin x dy 8 dz

Calculus
Application of derivativesUse Green s Theorem to find the counterclockwise circulation and outward flux for the field F y 2x i 2x y j and curve C the triangle bounded by y 0 x 3 a The flux is Simplify your answer
Calculus
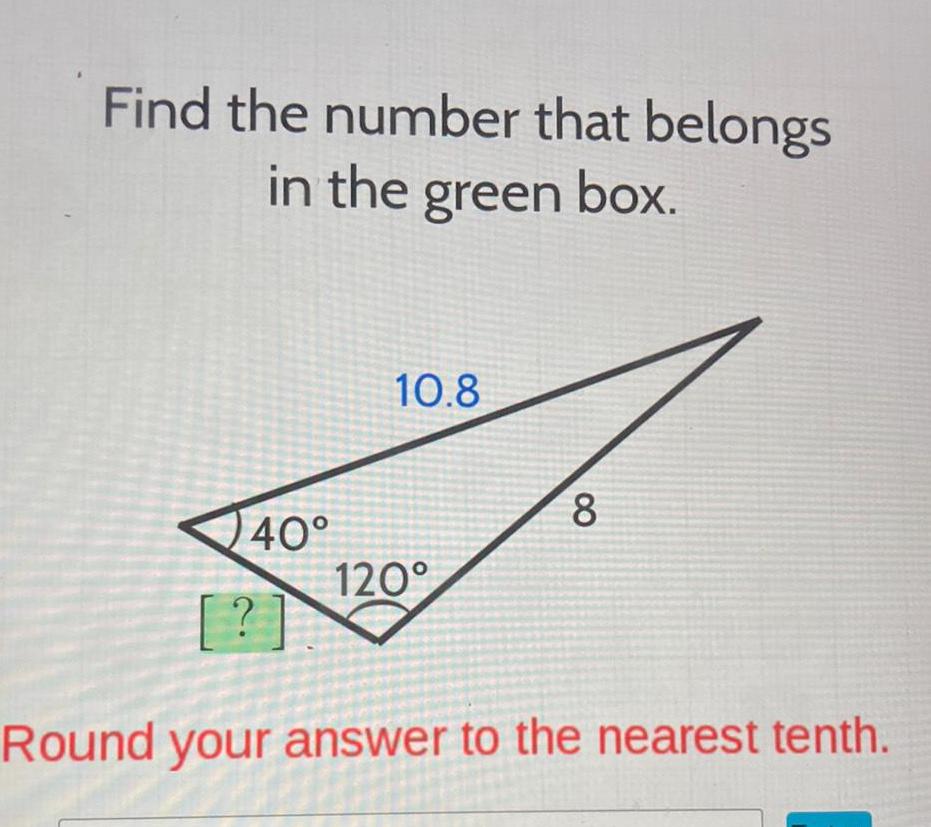
Application of derivativesFind the number that belongs in the green box 40 10 8 120 8 Round your answer to the nearest tenth
Calculus
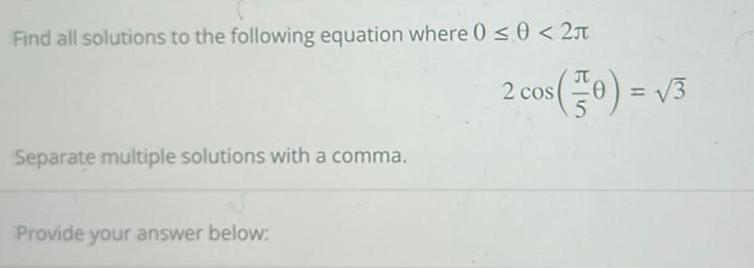
Application of derivativesFind all solutions to the following equation where 0 0 2 Separate multiple solutions with a comma Provide your answer below 2 cos 0 3
Calculus
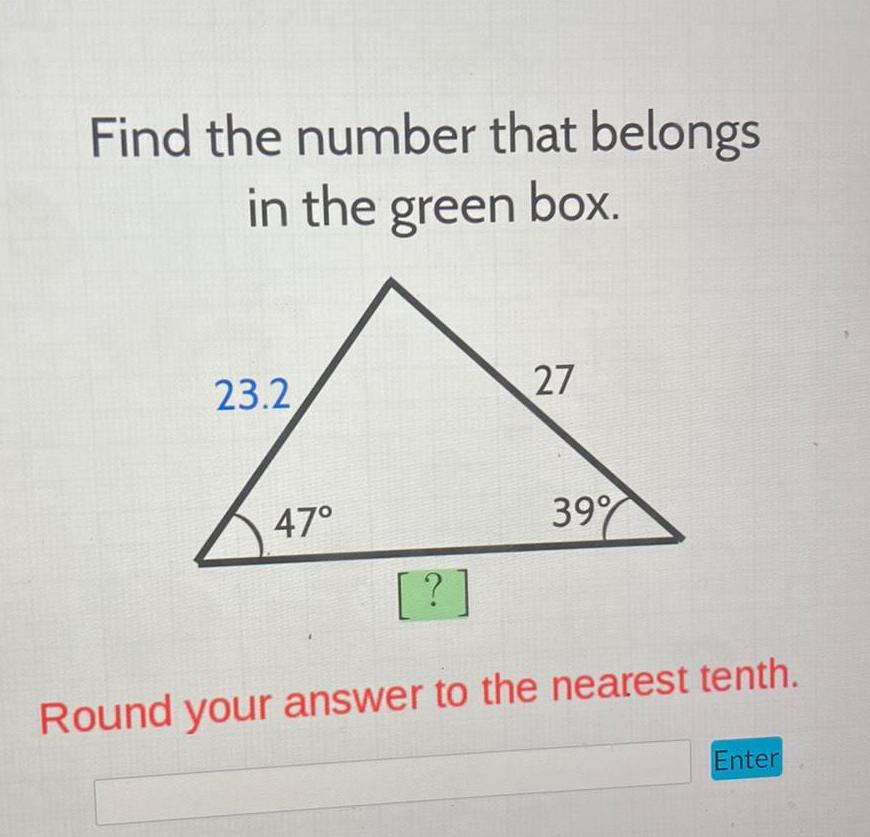
Application of derivativesFind the number that belongs in the green box 23 2 47 27 39 Round your answer to the nearest tenth Enter
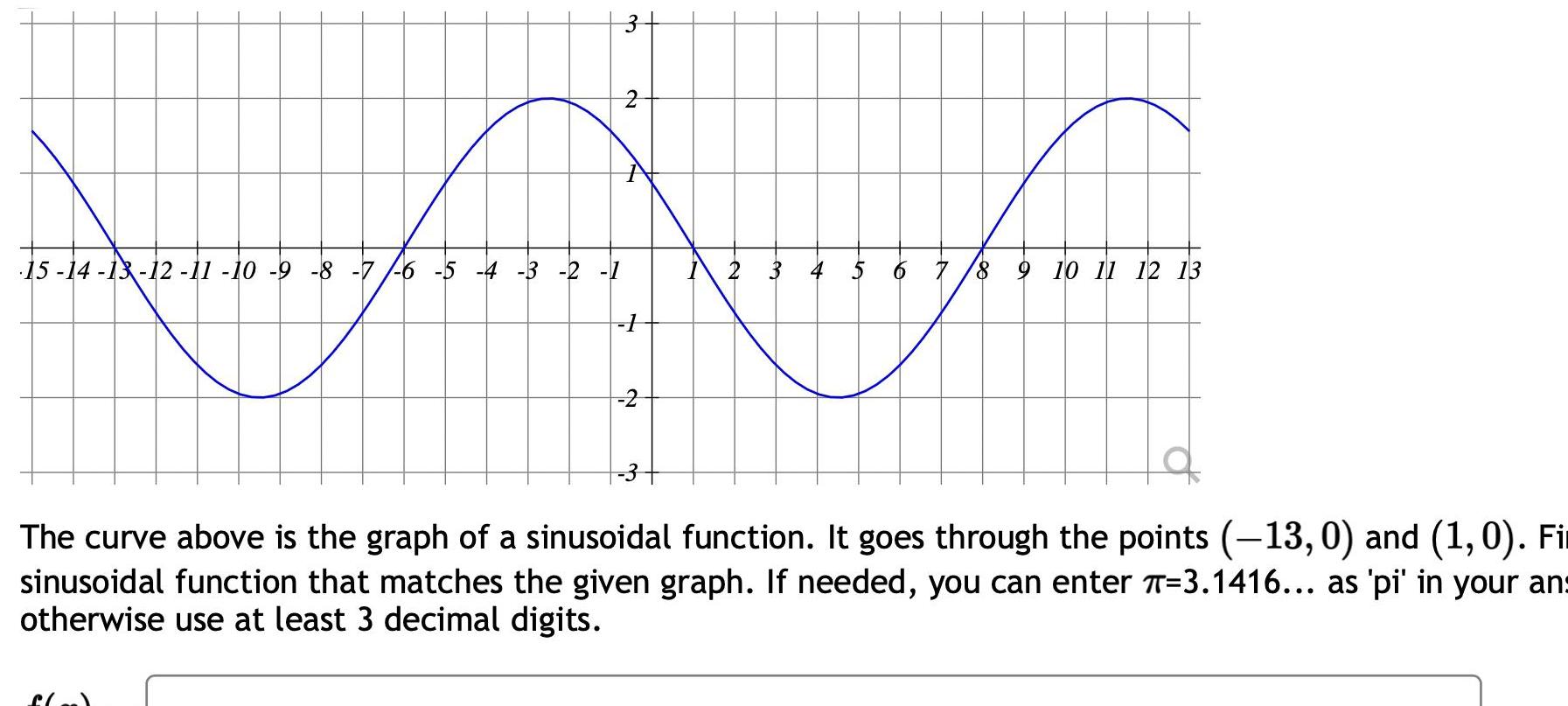
Calculus
Limits & Continuity15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 3 f o N A N 1 2 3 4 5 6 7 8 9 10 11 12 13 The curve above is the graph of a sinusoidal function It goes through the points 13 0 and 1 0 Fi sinusoidal function that matches the given graph If needed you can enter T 3 1416 as pi in your an otherwise use at least 3 decimal digits
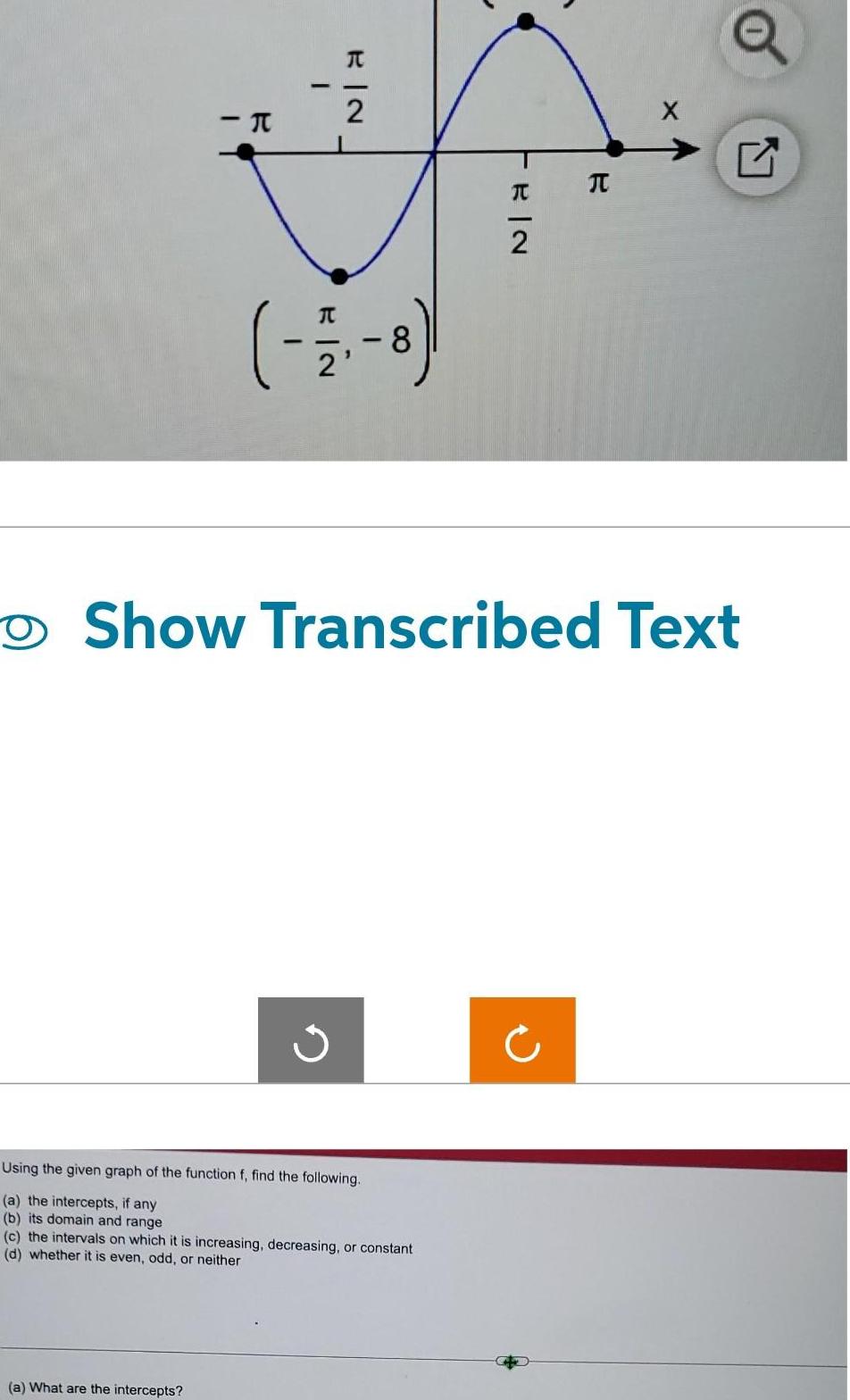
Calculus
Application of derivativesI H I a What are the intercepts RIN 2 17 8 Using the given graph of the function f find the following a the intercepts if any b its domain and range c the intervals on which it is increasing decreasing or constant d whether it is even odd or neither FEIN 2 Show Transcribed Text R Q
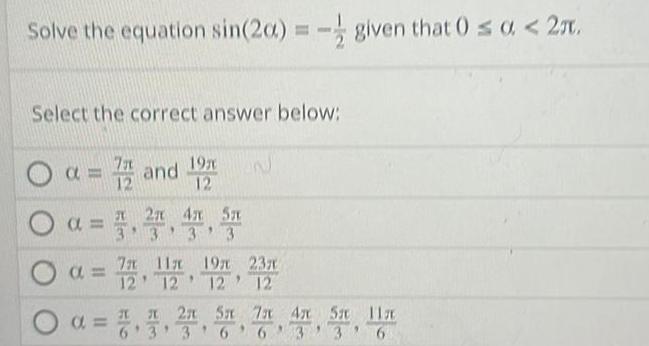
Calculus
DifferentiationSolve the equation sin 20 given that 0 0 2m Select the correct answer below a 72 and 192 a 3 O a 7 5m 11x 19 12 12 12 x 2 5 a 2 3 4 5 6 3 6 W 23 12 7 4x 5 11 63 31 AT ST

Calculus
Definite IntegralsUse a parametrization to express the area of the surface as a double integral Then evaluate the integral The portion of the cylinder x y 4 between the planes z 4 and z 7 Let uz and v 0 and use cylindrical coordinates to parameterize the surface Set up the double integral to find the surface area JO du dv 00 Type exact answers

Calculus
Vector CalculusSolve the following equation for where Select the correct answer below OB OB 2 OB 5 and B and 5 sec B 1 tan B 3 3

Calculus
Application of derivativesC 2 Before drawing any more graphs let s see what members of this family have in common Since 3 lim x x 2x c for any value of c they all have the x axis as a horizontal asymptote A vertical asymptote will occur when c 1 there is no vertical asymptote the top graph above When c 1 the graph has a single vertical asymptote x 1 because 3 lim x 1 x 2x 1 0 f x Now we compute the derivative When c 1 there are two vertical asymptotes x 1 3 lim x 1 x 1 x 2x c This shows that f x 0 when x maximum value f 1 0 For c 1 this means that f increases on the interval in interval notation if c 1 f x 0 when x 1 and f x 0 when x 1 the bottom graph above For c 1 f 1 0 Solving this equation we get x 1 and decreases on the interval in interval notation For c 1 there is an absolute is a local maximum value and the intervals of increase and decrease are interrupted at the vertical asymptotes When The figures below are a slide show displaying five members of the family all graphed in the viewing rectangle 5 4 by 6 6 As predicted c 1 is a value at which a transition takes place from 0 as c co As c decreases two vertical asymptotes to one and then to none As c increases from 1 we see that the maximum point becomes lower this is explained by the fact that c 1 1
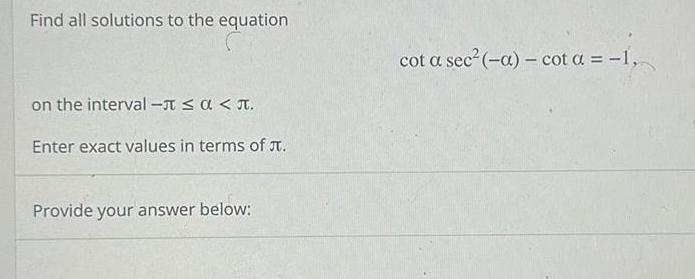
Calculus
Vector CalculusFind all solutions to the equation on the interval Enter exact values in terms of Provide your answer below cot a sec a cot a 1

Calculus
Limits & ContinuityGiven that 0 x 2 which of the following gives all solutions to the equation cos 2x cos x sin 2x sin x Select the correct answer below O C 5x X x 5 and 7 x 4 and 5 4x 5x 10x 11x 16x 17x 99

Calculus
Application of derivativesQuestion Solve the equation 3tan a 3tan a given that Separate your answers with commas

Calculus
Limits & ContinuitySolve the equation 2tan a 2tan a given that a T Separate your answers with commas

Calculus
Definite IntegralsProduce graphs of f that reveal all the important aspects of the curve Then use calculus to find the following Enter your answers using interval notation Round your answers to two decimal pla f x 8 sin x x 5 x 3 Find the interval s of increase Find the interval s of decrease Find the inflection points of the function smaller x value larger x value x y x y Find the interval s where the function is concave up Find the interval s where the function is concave down
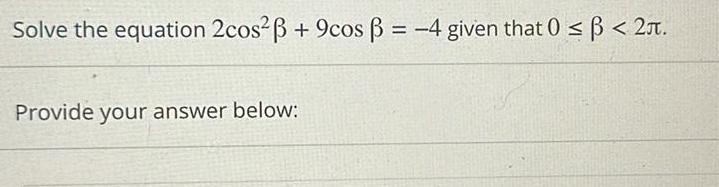

Calculus
Definite IntegralsFind f Use C for the constant of the first antiderivative D for the constant of the second antiderivative and F for the constant of the third antiderivative f t 24 cos t f t X Remember to use capital C D and F


Calculus
Limits & ContinuitySolve for 8sin 0 5 13 and 0 0 25 List your answers as exact answers in terms of separated by a comma if necessary Do not include 0 in your answer

Calculus
Limits & ContinuityDetermine all the values of 0 in the following equation if 0 0 2 12sin 0 5 4 Type your answers from least to greatest Provide your answer below

Calculus
Indefinite IntegrationConsider the following function f x 36x Find f x Use C for the constant of the first antiderivative f x Find f Use D for the constant of the second antiderivative f x

Calculus
Application of derivativesFind the antiderivative F off that satisfies the given condition Check your answer by comparing the graphs of f and F f x 2e 8x F 0 5 F x

Calculus
DifferentiationFind the most general antiderivative of the function Check your answer by differentiation Use C for the constant of the antiderivative 2t 4 7 t t F t f t

Calculus
Indefinite IntegrationFind an antiderivative of the function Remember to use absolute values where appropriate 5 t a g t G t b r 0 sec 0 R 8



Calculus
DifferentiationSolve for 0 if 10sin 0 8 5 3 8 and 0 0 2 Select the correct answer below 0 0 4 0 0 5 00 only only only 0 and 0 0 0 4 and 0 Sa 4x

Calculus
Limits & ContinuityIf 2 2 2cos 0 2 where 0 0 2 what are the values of 0 Select the correct answer below 0 2 and 0 0 O 0 0 only 0 0 and 0 0 0 only 7x 0 0 7 only 7x

Calculus
Indefinite IntegrationWe have determined that w 22 Recalling from a previous step that 44 w allows us to determine the other dimension 1 44 w To conclude we state the dimensions of the rectangle in m with perimeter 88 m whose area is as large as possible Enter the dimensions as a comma separated list m
Calculus
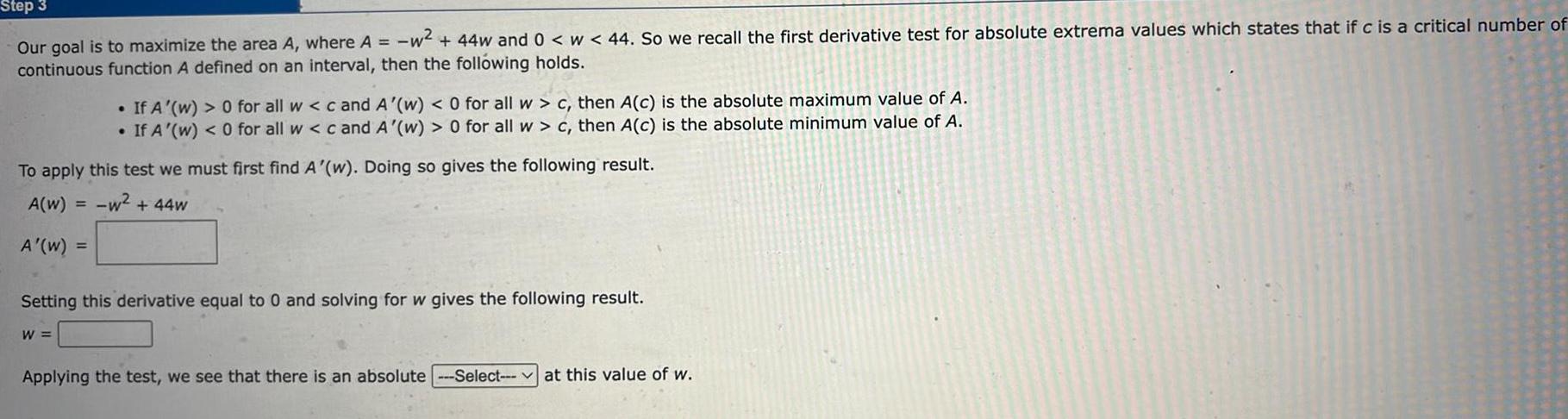
Application of derivativesStep 3 our goal is to maximize the area A where A w 44w and 0 w 44 So we recall the first derivative test for absolute extrema values which states that if c is a critical number of continuous function A defined on an interval then the following holds To apply this test we must first find A w Doing so gives the following result A W w 44w A W W If A w 0 for all w c and A w 0 for all w c then A c is the absolute maximum value of A If A w 0 for all w c and A w 0 for all w c then A c is the absolute minimum value of A Setting this derivative equal to 0 and solving for w gives the following result Applying the test we see that there is an absolute Select at this value of w

Calculus
Application of derivativesWe are given that the perimeter of the rectangle is 88 m Therefore P 88 We substitute this value into the perimeter equation determined in the previous step P 21 2w 88 2 2w We then solve the resulting equation for I 88 2 2w 1 Next we substitute this expression for into the area equation determined in the previous step and expand the result A lw A w Recalling that area must be greater 0 we note that this equation is valid when 0 W

Calculus
Application of derivativesWe have determined that the absolute minimum of f x occurs at x 28 where x is the smaller of the two numbers whose product we wish to minimize Recall that the other number is given by x 56 Thus the two numbers whose difference is 56 and whose product is a minimum are as follows smaller number larger number

Calculus
Application of derivativesWe wish to minimize this function so we recall the first derivative test for absolute extrema values which states that if c is a critical number of a continuous function f defined on an interv then the following holds If f x 0 for all x c and f x 0 for all x c then f c is the absolute maximum value of f If f x 0 for all x c and f x 0 for all x c then f c is the absolute minimum value of f To apply this test we must first find f x Doing so gives the following result f x x 56x f x Setting this derivative equal to 0 and solving for x gives the following result X Applying the test we see that there is an absolute Select at this value of x

Calculus
Application of derivativesIf C x is the cost of producing x units of a commodity then the average cost per unit is c x C x 3 000 110x 6x 2 a Find the total cost in dollars at a production level of 1 000 units b Find the average cost in dollars per unit at a production level of 1 000 units per unit c Find the marginal cost in dollars per unit at a production level of 1 000 units per unit d Find the production level in units that will minimize the average cost units e What is the minimum average cost in dollars per unit per unit C x X Consider the cost function C x given below Round your answers to the nearest cent

Calculus
Application of derivativesIf 30 000 cm of material is available to make a box with a square base and an open top find the largest possible volume in cm of the box 3 cm

Calculus
Application of derivativesConsider the following problem a farmer with 750 feet of fencing wants to enclose a rectangular area and then divide it into four pens with fencing parallel to one side of the rectangle What is largest possible total area of the four pens a Draw several diagrams illustrating the situation some with shallow wide pens and some with deep narrow pens Find the total areas of these configurations Does it appear that there is maximum area If so estimate it b Draw a diagram illustrating the general situation Let x denote the length of each of two sides and three dividers Let y denote the length of the other two sides c Write an expression for the total area A in terms of both x and y A d Use the given information to write an equation that relates the variables e Use part d to write the total area as a function of one variable A x f Finish solving the problem by finding the largest area in ft ft

Calculus
Limits & ContinuityWe will now write a function that is the product of our two numbers where x represents the smaller number and x 56 represents the larger number as follows f x x x x
Calculus
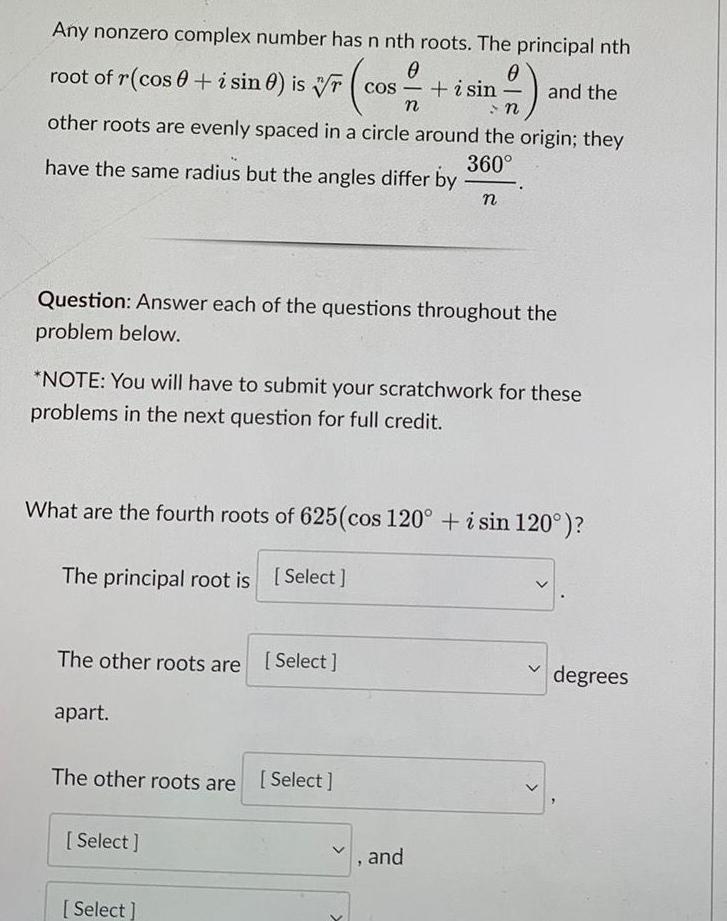
Application of derivativesAny nonzero complex number has n nth roots The principal nth root of r cos i sin 0 is rcos i sin 0 cos n other roots are evenly spaced in a circle around the origin they have the same radius but the angles differ by 360 Question Answer each of the questions throughout the problem below NOTE You will have to submit your scratchwork for these problems in the next question for full credit The other roots are Select apart What are the fourth roots of 625 cos 120 i sin 120 The principal root is Select The other roots are Select Select and the n Select 7 and degrees

Calculus
DifferentiationFind the dimensions of a rectangle in m with perimeter 76 m whose area is as large as possible Enter the dimensions as a comma separated list m

Calculus
Limits & ContinuityLet and w represent the length and the width of the rectangle measured in m Let A represent the area of the rectangle measured in m Writing an equation for A in terms of I and w gives us the following A m Let P represent the perimeter of the rectangle measured in m Writing an equation for P in terms of and w gives us the following P m