continuous at every point in its domain and hence f is a

Last updated: 10/10/2023

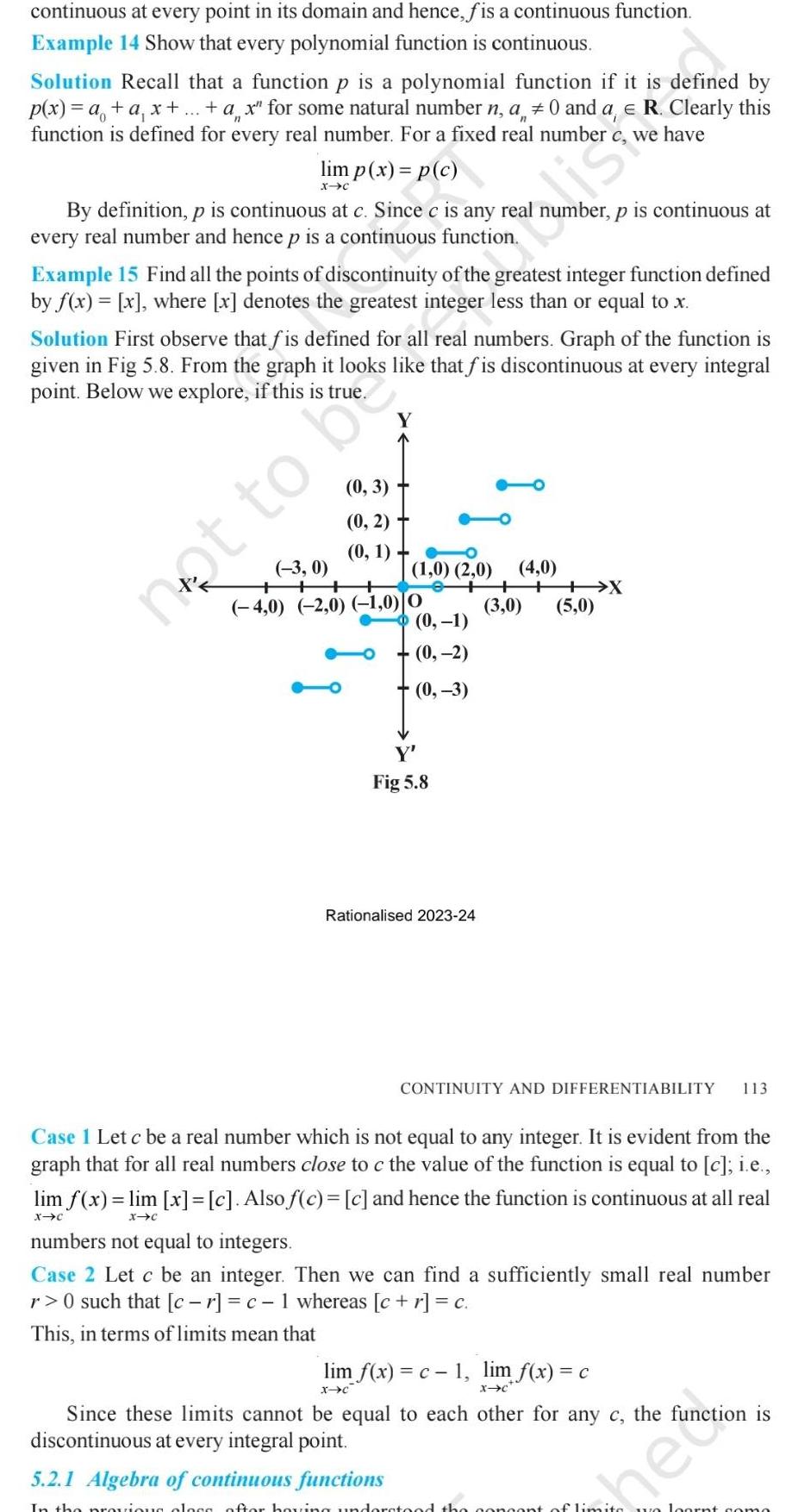
continuous at every point in its domain and hence f is a continuous function Example 14 Show that every polynomial function is continuous Solution Recall that a function p is a polynomial function if it is defined by p x a a x ax for some natural number n a 0 and a e R Clearly this function is defined for every real number For a fixed real number c we have lim p x p c X C By definition p is continuous at c Since c is any real number p is continuous at every real number and hence p is a continuous function Example 15 Find all the points of discontinuity of the greatest integer function defined by f x x where x denotes the greatest integer less than or equal to x Solution First observe that fis defined for all real numbers Graph of the function is given in Fig 5 8 From the graph it looks like that fis discontinuous at every integral point Below we explore if this is true Y 0 3 0 2 0 1 3 0 4 0 2 0 1 0 0 1 0 2 0 not to b 0 1 0 2 0 3 Y Fig 5 8 Rationalised 2023 24 4 0 3 0 X 5 0 CONTINUITY AND DIFFERENTIABILITY 113 Case I Let c be a real number which is not equal to any integer It is evident from the graph that for all real numbers close to c the value of the function is equal to c i e lim f x lim x c Also f c c and hence the function is continuous at all real X C X C numbers not equal to integers Case 2 Let c be an integer Then we can find a sufficiently small real number r 0 such that cr c 1 whereas c r c This in terms of limits mean that lim f x c 1 lim f x c X C X C Since these limits cannot be equal to each other for any c the function is discontinuous at every integral point 5 2 1 Algebra of continuous functions In the previous clogs after having understood the concept of limits we loont como he Anction