Converting P 36 39 x 38 39 to the standard normal random
Last updated: 11/21/2023
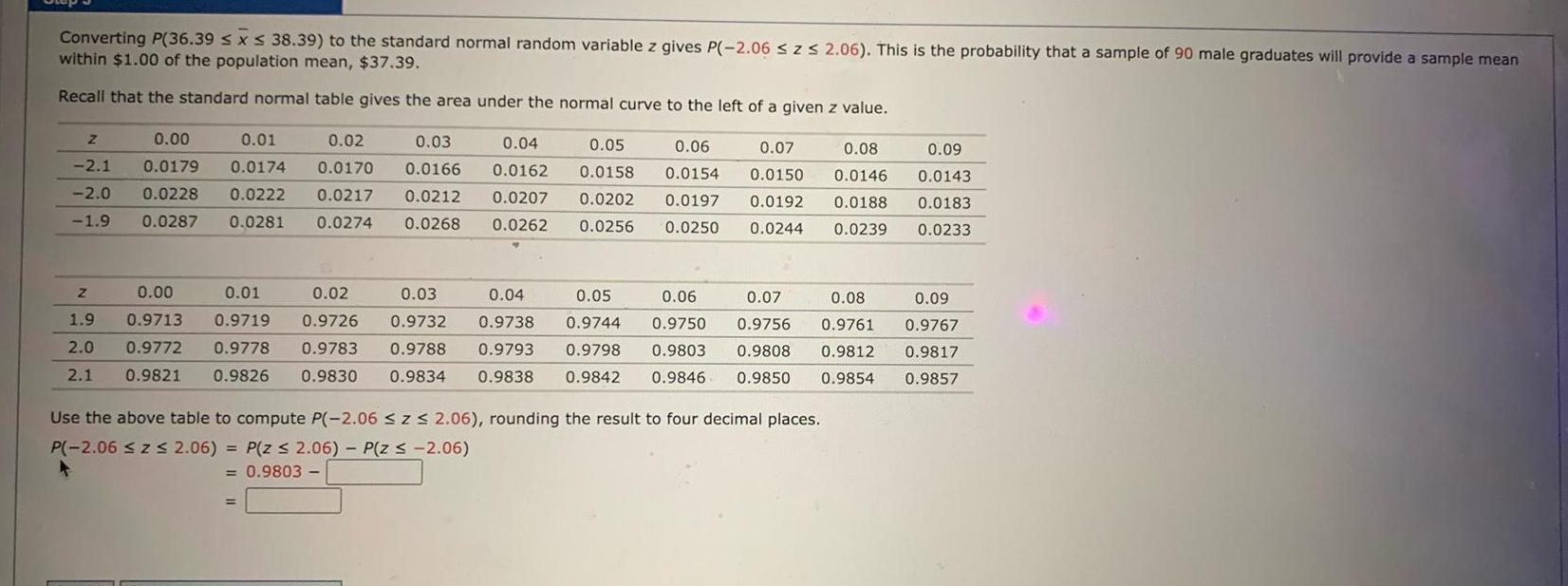
Converting P 36 39 x 38 39 to the standard normal random variable z gives P 2 06 z 2 06 This is the probability that a sample of 90 male graduates will provide a sample mean within 1 00 of the population mean 37 39 Recall that the standard normal table gives the area under the normal curve to the left of a given z value Z 0 00 0 01 0 02 0 03 0 04 0 05 0 06 0 07 0 08 2 1 0 0179 0 0174 0 0170 0 0166 0 0162 0 0158 0 0154 0 0150 0 0146 2 0 0 0228 0 0222 0 0217 0 0212 0 0207 0 0202 0 0197 0 0192 0 0188 1 9 0 0287 0 0281 0 0274 0 0268 0 0262 0 0256 0 0250 0 0244 0 0239 Z 0 00 0 01 0 02 0 03 0 04 0 05 0 06 1 9 0 9713 0 9719 0 9726 0 9732 0 9738 0 9744 0 9750 2 0 0 9772 0 9778 0 9783 0 9788 0 9793 0 9798 0 9803 2 1 0 9821 0 9826 0 9830 0 9834 0 9838 0 9842 0 9846 0 9850 0 07 0 08 0 9756 0 9761 0 9808 0 9812 0 9854 Use the above table to compute P 2 06 z 2 06 rounding the result to four decimal places P 2 06 z 2 06 P Z 2 06 P z 2 06 0 9803 0 09 0 0143 0 0183 0 0233 0 09 0 9767 0 9817 0 9857