Find the derivative of the function f t 6t sin nt Step 1 We

Last updated: 6/12/2023

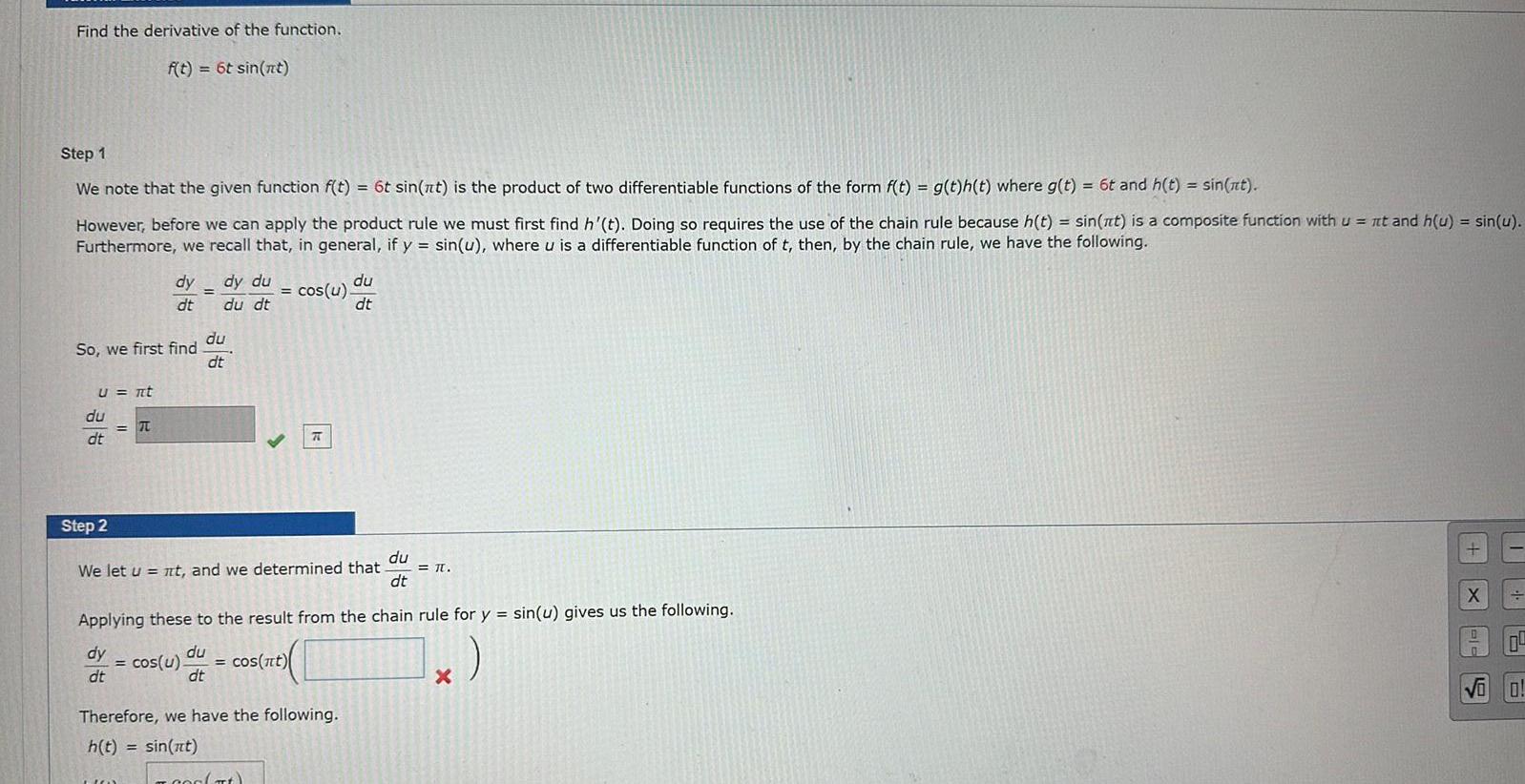
Find the derivative of the function f t 6t sin nt Step 1 We note that the given function f t 6t sin nt is the product of two differentiable functions of the form f t g t h t where g t 6t and h t sin t However before we can apply the product rule we must first find h t Doing so requires the use of the chain rule because h t sin nt is a composite function with u it and h u sin u Furthermore we recall that in general if y sin u where u is a differentiable function of t then by the chain rule we have the following So we first find U It du dt Step 2 70 dy dy du du dt dt itor du dt cos u COC Tt 70 du We let u t and we determined that dt Applying these to the result from the chain rule for y sin u gives us the following dy cos u cos nt du dt dt Therefore we have the following h t sin at du dt TU X 15 Vo 0