Given the function g(x) = 8x^33 + 36x^2 + 48x, find the

Last updated: 8/11/2022

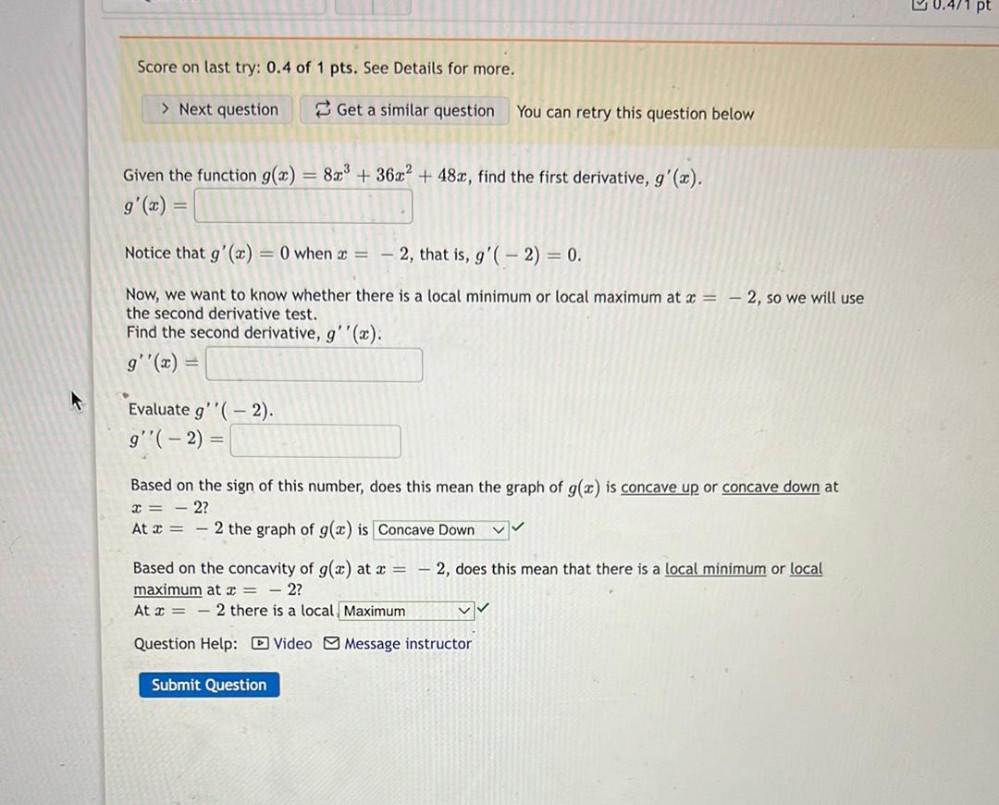
Given the function g(x) = 8x^33 + 36x^2 + 48x, find the first derivative, g'(x)=______________ Notice that g'(x) = 0 when x = -2, that is, g'( - 2) = 0. Now, we want to know whether there is a local minimum or local maximum at x = -2, so we will use the second derivative test. Find the second derivative, g''(x). g''(x)=____________ Evaluate g''(-2). g''( - 2) =_______________ Based on the sign of this number, does this mean the graph of g(x) is concave up or concave down at x= - 2? At x = – 2 the graph of g(x) is ____________ Based on the concavity of g(x) at x = – 2, does this mean that there is a local minimum or local maximum at x= - 2? At x = - 2 there is a ____________