Given x and x distributions that are normal or approximately

Last updated: 11/5/2023

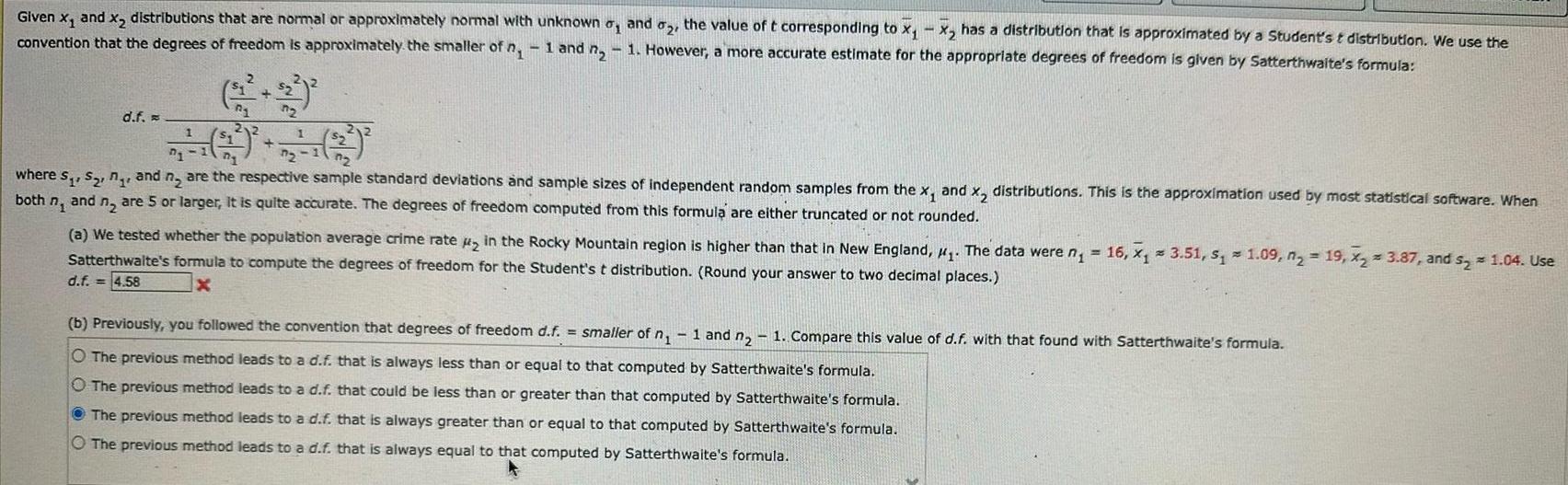
Given x and x distributions that are normal or approximately normal with unknown and 2 the value of t corresponding to x x has a distribution that is approximated by a Student s t distribution We use the convention that the degrees of freedom is approximately the smaller of n 1 and 1 However a more accurate estimate for the appropriate degrees of freedom is given by Satterthwaite s formula 2 3 d f where s S n and n are the respective sample standard deviations and sample sizes of independent random samples from the x and x distributions This is the approximation used by most statistical software When both n and n are 5 or larger it is quite accurate The degrees of freedom computed from this formula are either truncated or not rounded a We tested whether the population average crime rate in the Rocky Mountain region is higher than that in New England The data were n Satterthwalte s formula to compute the degrees of freedom for the Student s t distribution Round your answer to two decimal places d f 4 58 16 3 51 S 1 09 n 19 X 3 87 and s 1 04 Use b Previously you followed the convention that degrees of freedom d f smaller of n 1 and n 1 Compare this value of d f with that found with Satterthwaite s formula O The previous method leads to a d f that is always less than or equal to that computed by Satterthwaite s formula O The previous method leads to a d f that could be less than or greater than that computed by Satterthwaite s formula The previous method leads to a d f that is always greater than or equal to that computed by Satterthwaite s formula O The previous method leads to a d f that is always equal to that computed by Satterthwaite s formula