Lesson 7 1 Interior and Exterior Angles Learning Goal I can
Last updated: 11/28/2023
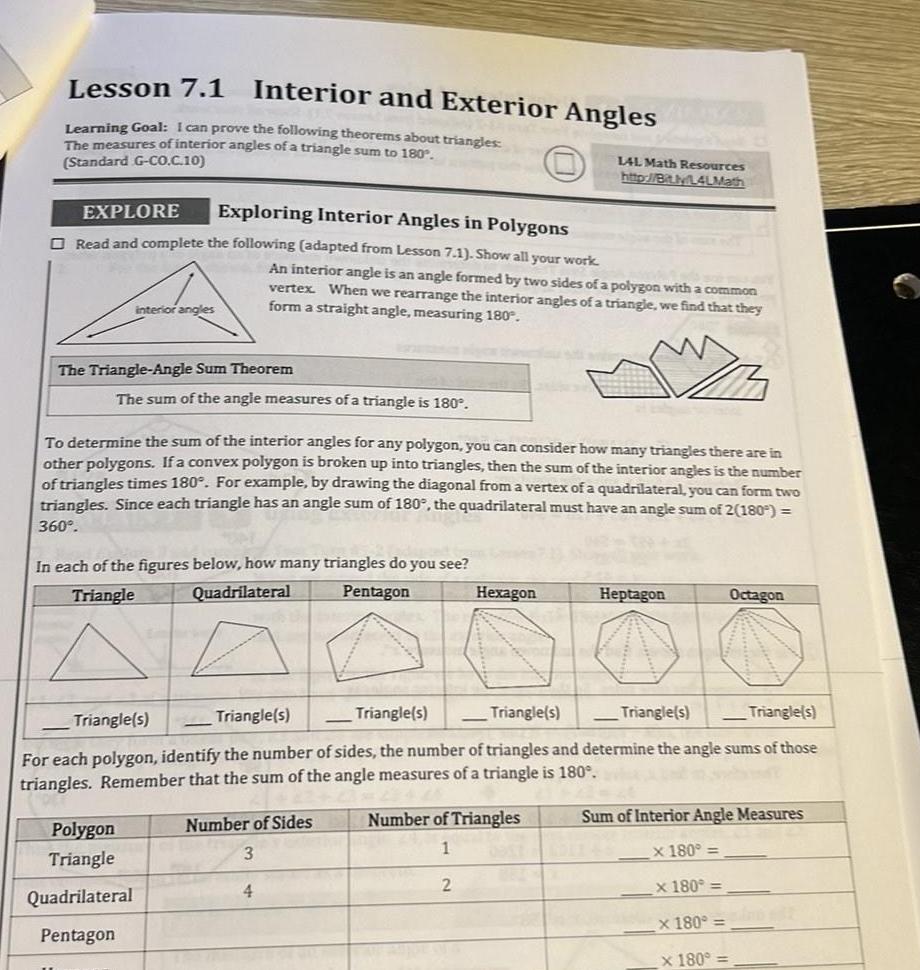
Lesson 7 1 Interior and Exterior Angles Learning Goal I can prove the following theorems about triangles The measures of interior angles of a triangle sum to 180 Standard G CO C 10 EXPLORE Exploring Interior Angles in Polygons Read and complete the following adapted from Lesson 7 1 Show all your work interior angles The Triangle Angle Sum Theorem An interior angle is an angle formed by two sides of a polygon with a common vertex When we rearrange the interior angles of a triangle we find that they form a straight angle measuring 180 The sum of the angle measures of a triangle is 180 To determine the sum of the interior angles for any polygon you can consider how many triangles there are in other polygons If a convex po is broken up into triangles then the sum of the interior angles is the number of triangles times 180 For example by drawing the diagonal from a vertex of a quadrilateral you can form two triangles Since each triangle has an angle sum of 180 the quadrilateral must have an angle sum of 2 180 360 In each of the figures below how many triangles do you see Triangle Quadrilateral Pentagon Polygon Triangle Quadrilateral Pentagon Number of Sides 3 4 LAL Math Resources http bit ly L4LMath Hexagon Triangle s Triangle s Triangle s Triangle s Triangle s Triangle s For each polygon identify the number of sides the number of triangles and determine the angle sums of those triangles Remember that the sum of the angle measures of a triangle is 180 Number of Triangles 1 2 Heptagon Octagon Sum of Interior Angle Measures x 180 x 180 x 180 x 180