Question:
Let a ≠ 1 and a5 = 1. Then prove that Q(a) is a normal
Last updated: 8/1/2022
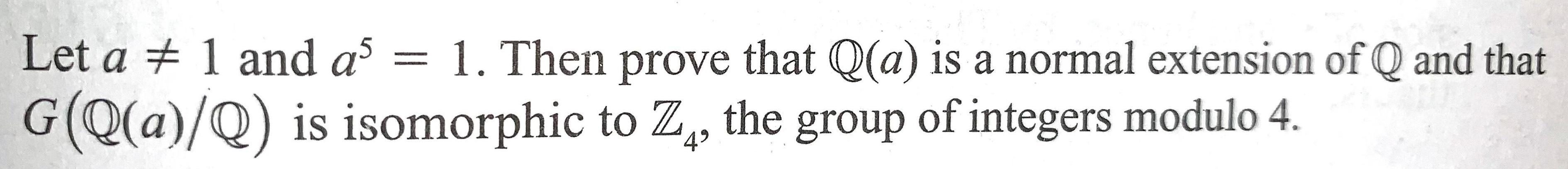
Let a ≠ 1 and a5 = 1. Then prove that Q(a) is a normal extension of Q and that G(Q(a)/Q) is isomorphic to Z4, the group of integers modulo 4.
Last updated: 8/1/2022
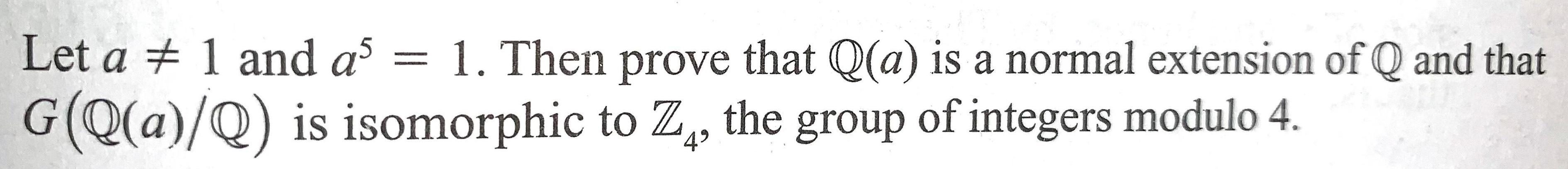
Let a ≠ 1 and a5 = 1. Then prove that Q(a) is a normal extension of Q and that G(Q(a)/Q) is isomorphic to Z4, the group of integers modulo 4.