Let F be a field and F is a fixed algebric closure of F.

Last updated: 7/16/2022

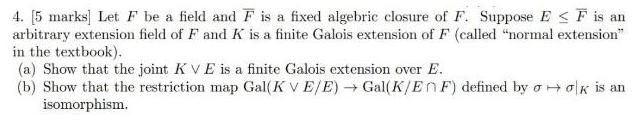
Let F be a field and F is a fixed algebric closure of F. Suppose E≤ F is an arbitrary extension field of F and K is a finite Galois extension of F (called "normal extension" in the textbook). (a) Show that the joint K VE is a finite Galois extension over E. (b) Show that the restriction map Gal(KVE/E) → Gal(K/EnF) defined by ook is an isomorphism.