Question:
Let G be a finite group and p be a prime number. Let H be a
Last updated: 7/31/2022
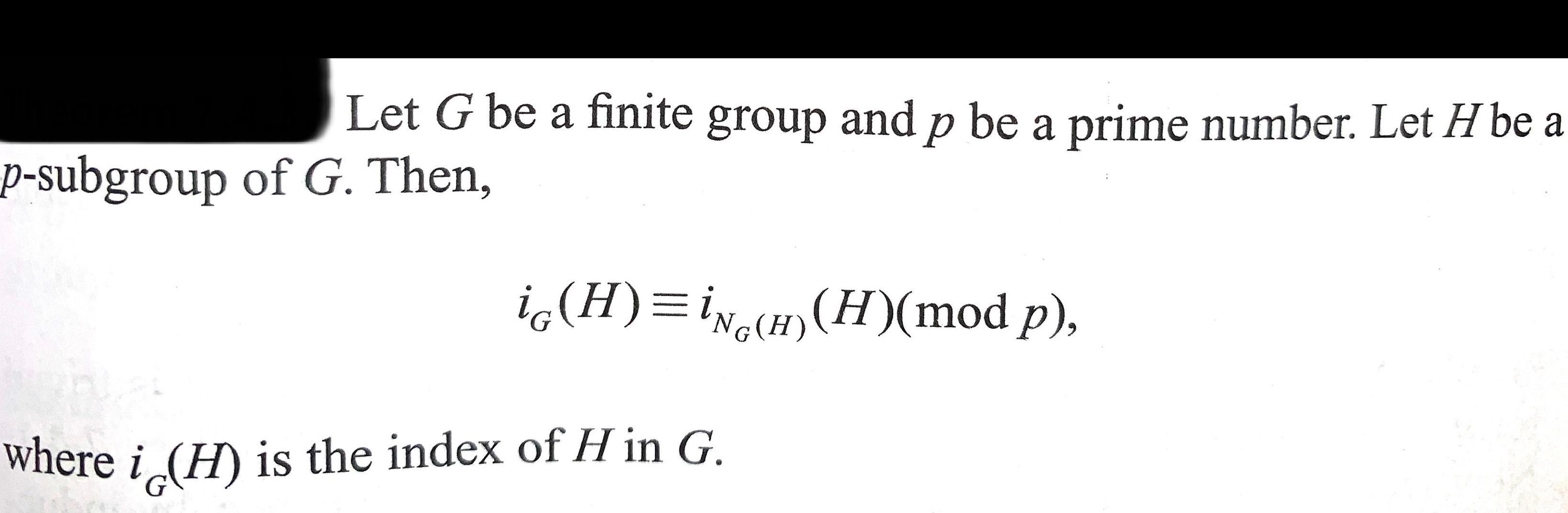
Let G be a finite group and p be a prime number. Let H be a p-subgroup of G. Then, iG(H)=iNG(H)(H)(mod p), where iG(H) is the index of H in G.
Last updated: 7/31/2022
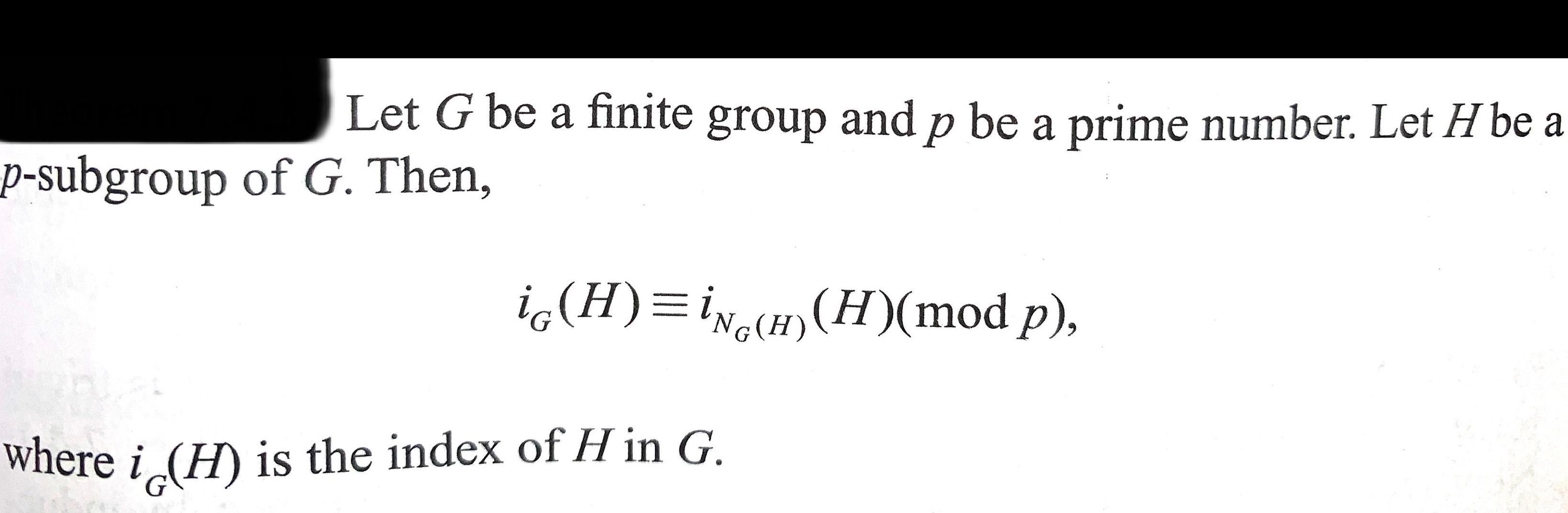
Let G be a finite group and p be a prime number. Let H be a p-subgroup of G. Then, iG(H)=iNG(H)(H)(mod p), where iG(H) is the index of H in G.