Let N = {1, 2, 3, 4, ...} be the set of natural numbers and

Last updated: 7/5/2022

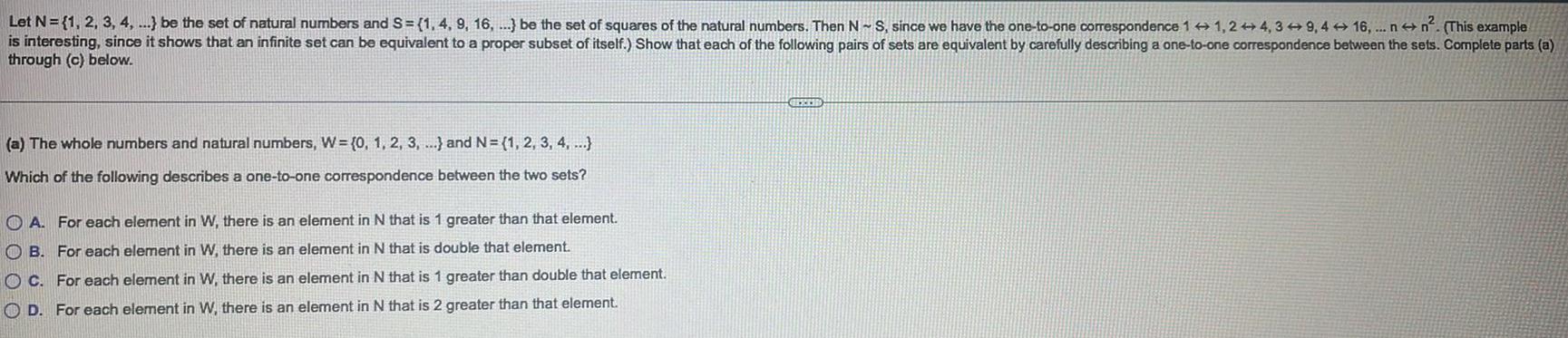
Let N = {1, 2, 3, 4, ...} be the set of natural numbers and S= (1, 4, 9, 16, ...) be the set of squares of the natural numbers. Then N - S, since we have the one-to-one correspondence 1+1, 2+4, 39, 416, ... nn². (This example is interesting since it shows that an infinite set can be equivalent to a proper subset of itself.) Show that each of the following pairs of sets are equivalent by carefully describing a one-to-one correspondence between the sets. Complete parts (a) through (c) below. (a) The whole numbers and natural numbers, W= {0, 1, 2, 3, ...) and N= {1, 2, 3, 4, ...) Which of the following describes a one-to-one correspondence between the two sets? A. For each element in W, there is an element in N that is 1 greater than that element. B. For each element in W, there is an element in N that is double that element. OC. For each element in W, there is an element in N that is 1 greater than double that element. D. For each element in W, there is an element in N that is 2 greater than that element.