Step 5 Now we must find the radius of convergence for the

Last updated: 7/22/2023

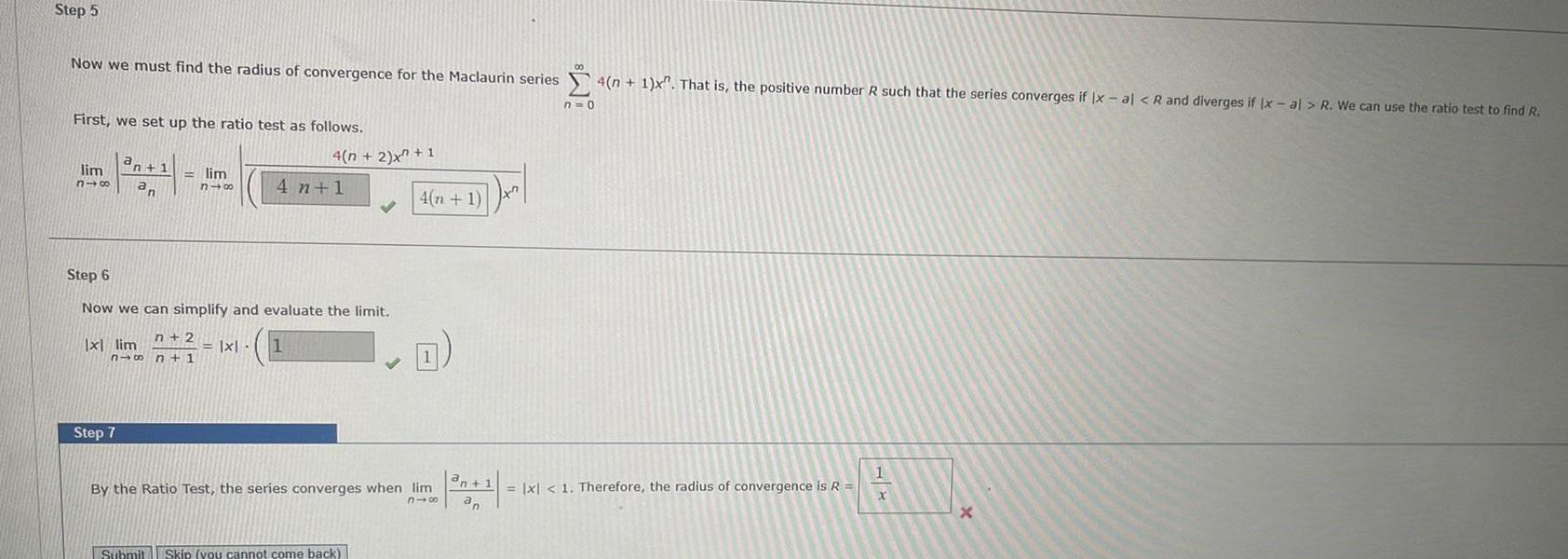
Step 5 Now we must find the radius of convergence for the Maclaurin series First we set up the ratio test as follows a lim n 1 318 an lim n48 n 2 816 n 1 x lim Step 7 Step 6 Now we can simplify and evaluate the limit 4 n 2 x 1 4 n 1 x 1 Submit Skip you cannot come back 4 n 1 x By the Ratio Test the series converges when lim 816 an 1 an 4 n 1 x That is the positive number R such that the series converges if x al R and diverges if Ix al R We can use the ratio test to find R n 0 x 1 Therefore the radius of convergence is R 1 X X