vausvAI The objective function is maximization so the

Last updated: 10/9/2023

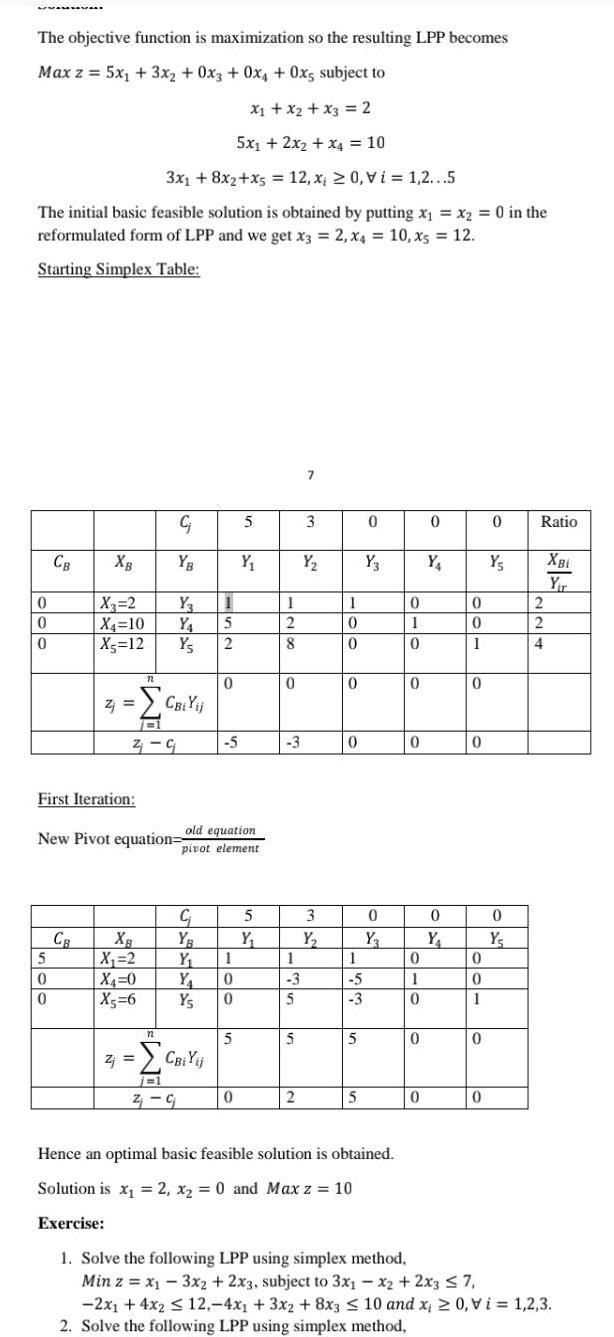
vausvAI The objective function is maximization so the resulting LPP becomes Max z 5x 3x 0x3 0x4 0x5 subject to X x2 x3 2 5x 2x x 10 3x1 8x2 x5 12 x 20 Vi 1 2 5 The initial basic feasible solution is obtained by putting x x2 0 in the reformulated form of LPP and we get x3 2 x4 10 x5 12 Starting Simplex Table 000 CB XB 5 0 0 1 X3 2 Y3 X4 10 Y4 5 X5 12 Y5 2 First Iteration CB 72 CBi Yij B1 Z G Z C YB XB X 2 X4 0 X5 6 New Pivot equation old equation pivot element Z 0 72 CBi Xij j 1 2 9 5 C YB Y 1 Y 0 Ys 0 5 5 0 Y 5 Y 1 2 8 0 3 1 3 5 5 2 7 3 Y 3 Y 1 0 0 0 0 1 5 3 5 5 0 Y3 0 Y3 Hence an optimal basic feasible solution is obtained Solution is x 2 x 0 and Max z 10 Exercise 0 1 0 0 0 0 1 0 0 0 0 Y 0 Y 0 0 1 0 0 0 0 1 0 0 1 Solve the following LPP using simplex method Min z x 3x2 2x3 subject to 3x1 x2 2x3 7 0 Y 0 Y Ratio 2 2 4 XBi Yir 2x 4x2 12 4x 3x2 8x3 10 and x 0 Vi 1 2 3 2 Solve the following LPP using simplex method