We are given the following power series and must determine the radius of convergence R centered at Recall that a power series

Question

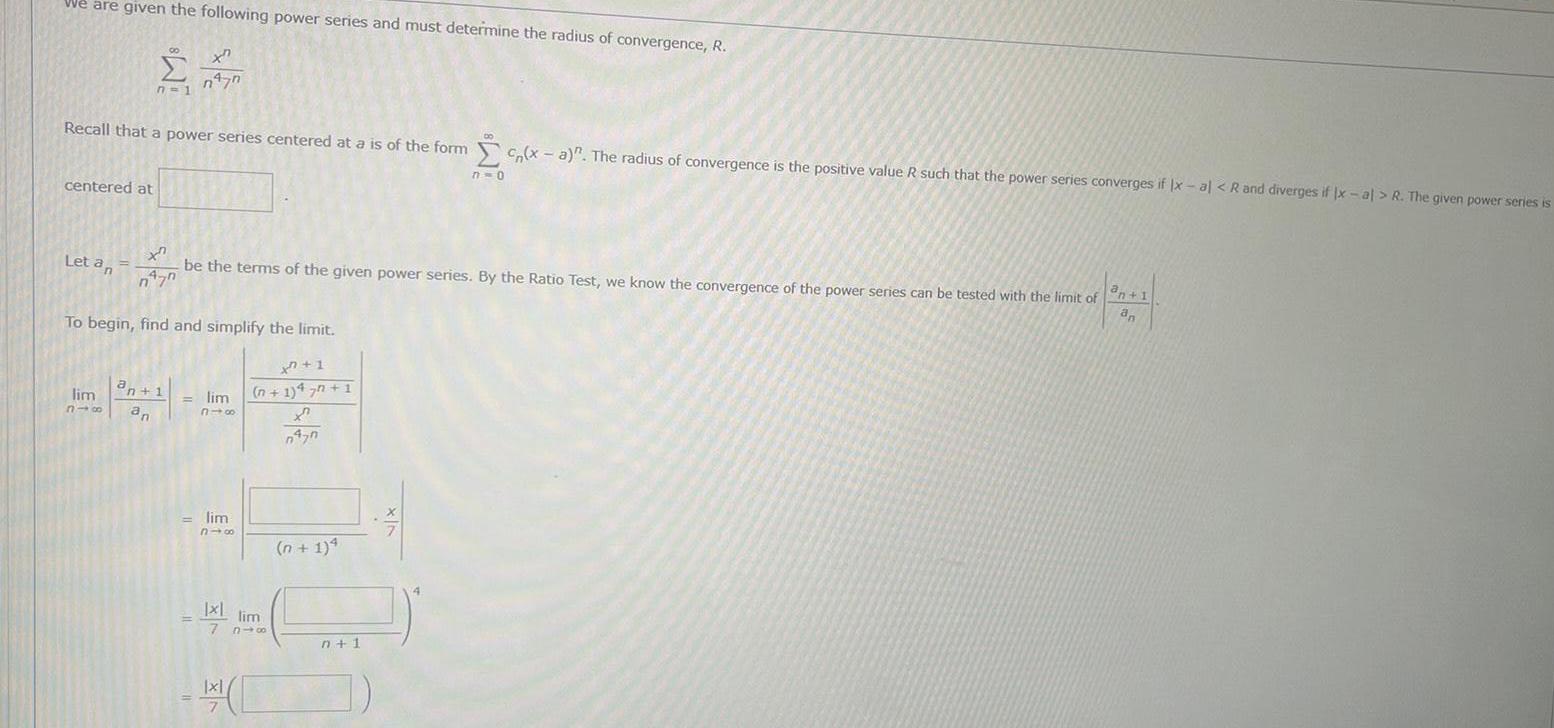
We are given the following power series and must determine the radius of convergence R centered at Recall that a power series centered at a is of the form x a The radius of convergence is the positive value R such that the power series converges if x al R and diverges if Ix al R The given power series is n 1 Let an xn n 70 be the terms of the given power series By the Ratio Test we know the convergence of the power series can be tested with the limit of an 1 an To begin find and simplify the limit xn 1 n 1 47n 1 X 0470 n477 lim an 1 318 an lim 318 lim 310 Ixl lim le 7 816 x n 1 4 7 0 n 1

Kunduz · Accepted Answer

Click to see the answer