Algebra Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.




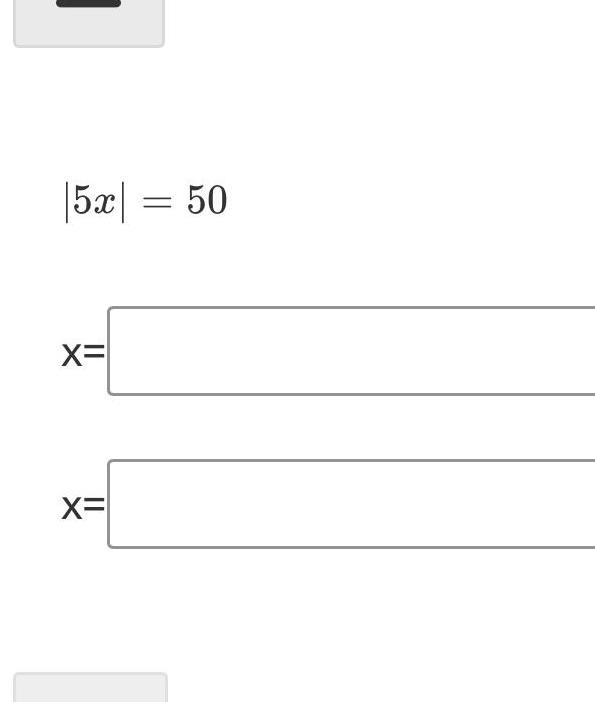
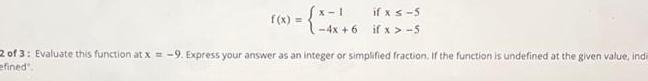
Algebra
Permutations and Combinationsf x if x 5 if x 5 4x 6 2 of 3 Evaluate this function at x 9 Express your answer as an integer or simplified fraction If the function is undefined at the given value inde efined
Algebra
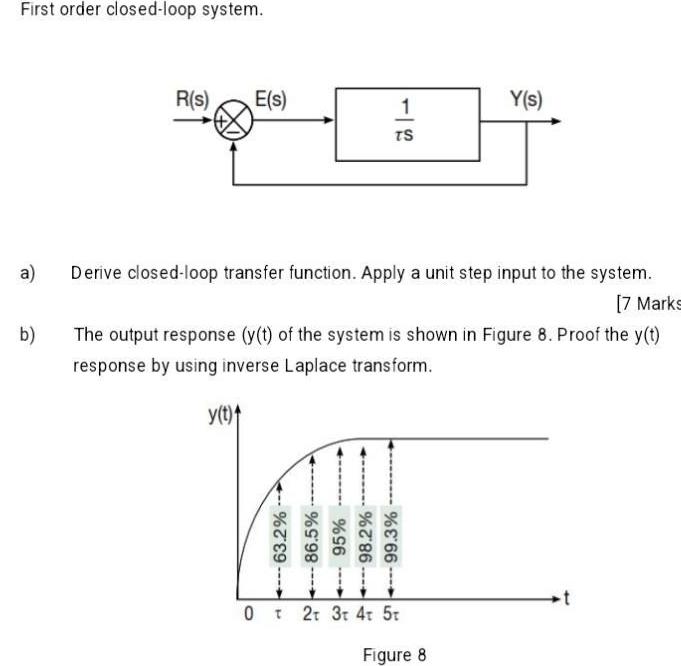
Complex numbersFirst order closed loop system a b R s E s 1 TS Derive closed loop transfer function Apply a unit step input to the system 7 Marks 63 2 N 86 5 The output response y t of the system is shown in Figure 8 Proof the y t response by using inverse Laplace transform y t 95 98 2 99 3 Y s 0 2T 3T 4t 5t Figure 8

Algebra
Matrices & Determinants3 Write the point slope form of the equation of the line through the given point with the given slope 9 8 through 3 2 slope 2 A y 2 2 x 3 B y 3 x 2 C y 3 x 2 D y 3 x 2 9 through 2 5 slope A y 2 x 5 B y 2 x 5 C y 2 x 5 D y 5 x 2 Write the point slope form of the equation of the line through the given points 10 through 5 1 and 5 1 11 11 through 1 3 and 0 3 A 0 x 5 A y 1 6 x 3 B y 1 x 5 B y 3 6 x 1 C y 1 x 5 D y 1 3 x 5 C y 3 x 1 6 D y 1 6 x 3 3 2

Algebra
Sequences & SeriesMATHEMATICS Proposition 3 Let x J 0 y J be two solutions of the initial value problem dx f t x x t xg dt then x t y t for all 1 JOJ Proof Recall that both x and y being solutions of the initial value problem satisfy the integral equations on their domain intervals x 1 x f s x s ds y 1 x f s y s ds Therefore x 1 y 1 ff s x s f s y s ds which implies 10 x 1 y 1 0 S 5 x s s y s 0 SK x s y s for all t2te 40 Applying Gronwalls result with A 0 we get 0 x 1 y 1 0 for all t t This gives the desired equality x t y t for all tJJ Towards the uniqueness of the solution of the initial value problem 3 we consider all the solutions of the initial value problem 3 Let the totality of them be denoted by x J XEA the solutions x being thus indexed by a suitable indexing set A Above we have verified that any two solutions say x and xare equal on the overlap of their domains Therefore we patch together all the solutions to get a maximal solution is the solution defined on the largest open interval It is obtained as follows Let J UJ 2 A clearly Jis an open sub internal of I with XJ and all the solutions x patch up to get a solution x J of the initial value problem 3

Algebra
Matrices & Determinants36 MATHEMATICS respectively Similarly in the second arrangement the entries in the first row represent the number of notebooks possessed by Radha Fauzia and Simran respectively The entries in the second row represent the number of pens possessed by Radha Fauzia and Simran respectively An arrangement or display of the above kind is called a matrix Formally we define matrix as Definition 1 A matrix is an ordered rectangular array of numbers or functions The numbers or functions are called the elements or the entries of the matrix We denote matrices by capital letters The following are some examples of matrices 2 5 A 0 5 3 6 B 3 5 3 2 i 3 Jou 1 7 5 N a 12 a22 m2 SUNNI In the above examples the horizontal lines of elements are said to constitute rows of the matrix and the vertical lines of elements are said to constitute columns of the matrix Thus A has 3 rows and 2 columns B has 3 rows and 3 columns while C has 2 rows and 3 columns 3 2 1 Order of a matrix A matrix having m rows and n columns is called a matrix of order m n or simply m n matrix read as an m by n matrix So referring to the above examples of matrices we have A as 3 x 2 matrix B as 3 x 3 matrix and C as 2 x 3 matrix We observe that A has 3 x 2 6 elements B and C have 9 and 6 elements respectively In general an m xn matrix has the following rectangular array C A 13 aj A23 x cosx sinx 2 or A almx 1 i m l j n i jEN n Thus the 7th row consists of the elements a consists of the elements a az azamj 1 x Rationalised 2023 24 am Azn in mn mxn a2 a3 ain while the 7th column In general a is an element lying in the 7th row and jth column We can also call it as the i j th element of A The number of elements in an m n matrix will be equal to mn MATRICES 37 Note In this chapter 1 We shall follow the notation namely A a to indicate that A is a matrix of order mx n

Algebra
Permutations and CombinationsNow Therefore a 12 11 3 1 1 a11 1 11 2 i 3j i 1 2 3 and j 1 2 12 3 11 12 3 21 2 213 3 11 0 a32 12 13 3 21 1 12 Hence the required matrix is given by A 0 3 For example A 1 1 2 5 92 111 3 21 2 3 3 Types of Matrices In this section we shall discuss different types of matrices i Column matrix A matrix is said to be a column matrix if it has only one column iii Square matrix 1 Rationalised 2023 24 In general A a mx is a column matrix of order m 1 1 Row matrix For example B 5 2 3 2 For example A A matrix is said to be a row matrix if it has only one row is a column matrix of order 4 1 3 3 2 In general B b 1 x is a row matrix of order is a row matr 2 Ban MATRICES n A matrix in which the number of rows equal to the number of columns said to be a square matrix Thus an m x n matrix is said to be a square matrix m n and is known as a square matrix of order n 1 0 3 2 1 3 oblished is a square matrix of order 3 3

Algebra
Quadratic equationsA square matrix B b mxm is said to be a diagonal matrix if all its non diagonal elements are zero that is a matrix B b mxm is said to be a diagonal matrix if b 0 when i j For example A 4 B of order 1 2 3 respectively v Scalar matrix For example A diagonal matrix is said to be a scalar matrix if its diagonal elements a that is a square matrix B b x is said to be a scalar matrix when i j when i j for some constant k A 3 B 1 1 C 0 b 0 ij b k C 0 coffe 0 are scalar matrices of order 1 2 and 3 respectively identity matrix if a kira of For example 1 3 0 1 1 O 0 0 20 0 03 vi Identity matrix A square matrix in which elements in the diagonal are all 1 and rest are all zero is called an identity matrix In other words the square matrix A a x is an 1 if i j if i j 1 are diagonal matrices We denote the identity matrix of order n by I When order is clear from the context we simply write it as I 1 00 0 1 0 00 1 e equal are identity matrices of order 1 2 and 3 Rationalised 2023 24 respectively Observe that a scalar matrix is an identity matrix when k 1 But every identity matrix is clearly a scalar matrix 0 0 For example 0 0 0 zero matrix by O Its order will be clear from the context MATRICES vii Zero matrix A matrix is said to be zero matrix or null matrix if all its elements are zero 3 3 1 Equality of matrices Definition 2 Two matrices A a and B b are said to be equal if i they are of the same order 41 0 0 are all zero matrices We denote ii each element of A is equal to the corresponding element of B that is a b for all i and j

Algebra
Quadratic equationsDefinition 2 Two matrices A a and B b are said to be equal if i they are of the same order ii each element of A is equal to the corresponding element of B that is a all i and j 3 For example 2 and 2 1 not equal matrices Symbolically if two matrices A and B are equal we write A B X y 1 5 0 If z a 2 b C 3 Example 4 If x 3 42 Simplifying we get 6 then 2 6 a 1 b 3 21 z 4 2y 7 MATHEMATICS 0 2 are equal matrices but Free 5 Find the values of a b c x y and z Solution As the given matrices are equal therefore their corresponding elements must be equal Comparing the corresponding elements we get x 3 0 z 4 6 2y 7 3y 2 a 1 3 b 3 2b 4 Solving these equations we get 1 In the matrix A 35 2 0 2c 2 a 2 b 7 c 1 x 3 y 5 z 2 Example 5 Find the values of a b c and d from the following equation 2a b a 2b 4 3 H 5c d 4c 3d 24 6 2b 4 21 0 6 3y 2 3 2c 2 Rationalised 2023 24 a 1 b 2 c 3 and d 4 19 5 Solution By equality of two matrices equating the corresponding elements we get 5c d 11 2a b 4 a 2b 3 4c 3d 24 EXERCISE 3 1 12 3 2 1 a 6 b 3 c 2 17 and write b for 3 1 5 i The order of the matrix ii The number of ele iii Write the elements a13 a21 9332 A242 23 2 If a matrix has 24 elements what are the possible has 13 elements are ned it can have What if it 3 If a matrix has 18 elements what are the possible orders it can have What if it hata

Algebra
Matrices & DeterminantsThis new matrix is the sum of the above two matrices We observe that the sum of two matrices is a matrix obtained by adding the corresponding elements of the given matrices Furthermore the two matrices have to be of the same order Thus if A 2 3 matrix Then we define A B Example 6 911 912 913 921 922 923 is a 2 x 3 matrix and B and is given by A B In general if A a and B b are two matrices of the same order say m n Then the sum of the two matrices A and B is defined as a matrix C c a b for all possible values of i and j 3 1 1 Since A B are of the same order 2 3 0 and B she a 1 b a 2 b 2 a21 b 1 a22 b 2 2 3 1 5 1 1 2 2 15 3 3 0 defined For example if A 2 51 2 3 b b2 b 3 b 1 b22 23 6 a 3 b 3 a23 b 3 is another 3 Therefore addition of A and B is defined 1 2 123 01 Note 1 We emphasise that if A and B are not of the same order then A B is not 13 3 B 1 then A B is not defined 2 We may observe that addition of matrices is an example of binary operation on the set of matrices of the same order 3 4 2 Multiplication of a matrix by a scalar Now suppose that Fatima has doubled the production at a factory A in all categories refer to 3 4 1

Algebra
Matrices & Determinantsiii Write the elements a3 a21 a332 a242 a23 2 If a matrix has 24 elements what are the possible orders it can have What if it has 13 elements 3 If a matrix has 18 elements what are the possib orders it can have What if it has 5 elements 4 Construct a 2 2 matrix A i j 2 5 Construct a 3 x 4 matrix whose elements are given by 1 aj 1 X 1 a ii a 2i j 6 Find the values of x y and z from the following equations 4 3 1 A x 35 3 a whose elements are given by 5 2 3x Z 7 Find the value of a b c and d from the equation a b 2a c 30 4 0 5 2a b 3c d 8 A am is a square matrix if n A m n B m n ii y 7 x y 2 5 z xy Rationalised 2023 24 0 y 2 4 62 58 Factory at A Boys Girls 13 C m n D None of these 9 Which of the given values of x and y make the following pair of matrices equal 3x 7 x 8 y 1 iii aij D x y present B Not possible to find 2 2 Boys 2 C y 7 x 3 3 3 10 The number of all possible matrices of order 3 x 3 with each entry 0 or 1 is A 27 B 18 C 81 Factory at B i 2j 2 x y z x Z y z MATRICES Girls II 3 4 Operations on Matrices In this section we shall introduce certain operations on matrices namely addition of matrices multiplication of a matrix by a scalar difference and multiplication of matrices 5 3 4 1 Addition of matrices Suppose Fatima has two factories at places A and B Each factory produces sport shoes for boys and girls in three different price categories labelled 1 2 and 3 The quantities produced by each factory are represented as matrices given below 43

Algebra
Quadratic equations1 y 3 x 1 2 a Graph the function by hand b Identify the vertex c Label at least one point on either side of the vertex d Take a picture of your graph and upload 2 Write a quadratic function in vertex form similar to 1 to model the graph G ve a reason for your answe 4 2 2 0 2

Algebra
Quadratic equationsBelle and her friends are planning a weekend trip to Isle of Palms South Carolina They can rent either a sedan or a fuel efficient SUV for the trip The sedan will cost 180 to rent while the SUV will cost 200 Belle estimates that the sedan will cost 0 11 per mile in fuel while the SUV will cost about 0 06 per mile How many miles would Belle and her friends need to drive for the total cost of the vehicles to be the same Simplify any fractions

Algebra
Complex numbers1 Solve by graphing y x 2x 1 y 2x 1 b x y 4 y 2x 2 Solve by substitution Show your work y x x 1 y x 1 3 Solve by elimination Show your work y 2 x 2 y x 4x 2
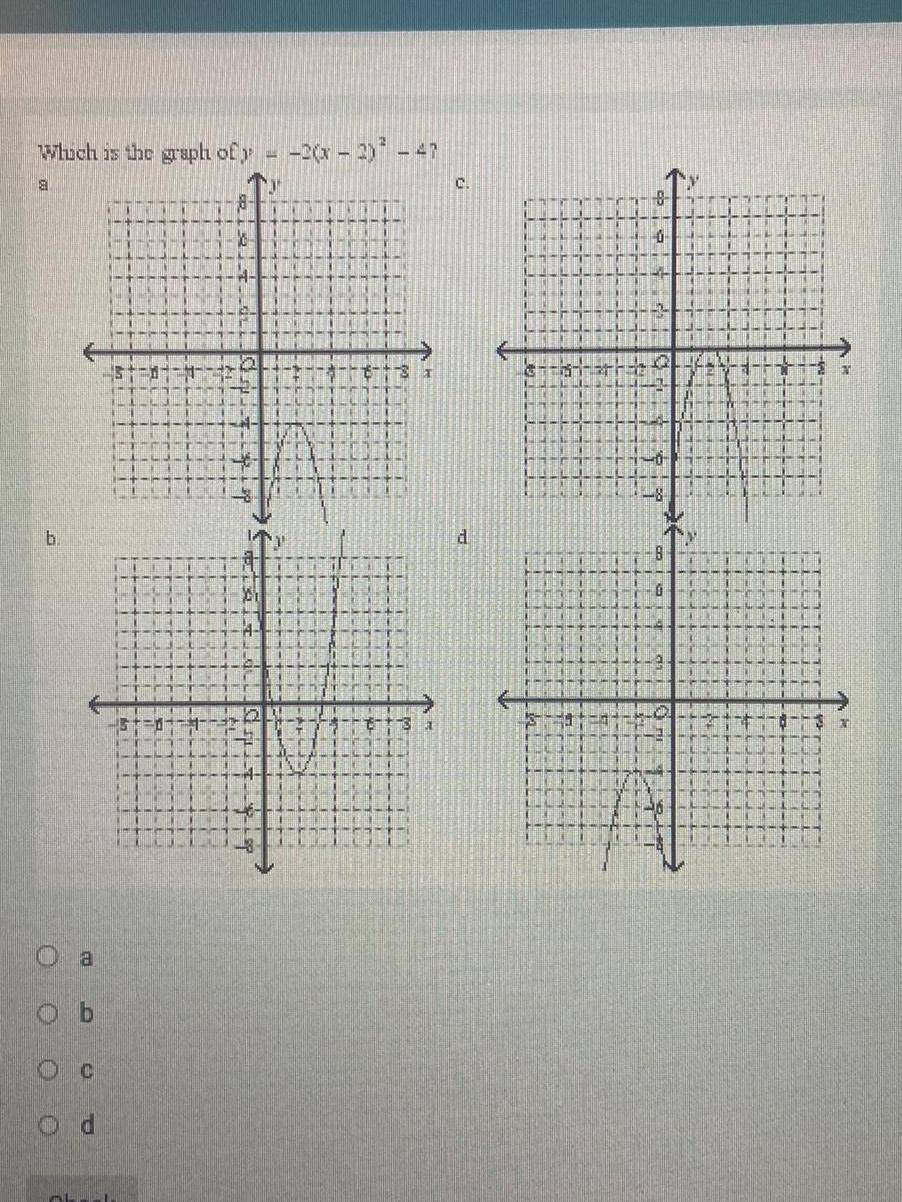
Algebra
Complex numbersy 2 x 1 1 Select one O a y 20 O b y21 O c y2 1 O d all real numbers Check Describe how to transform the parent function y x to the graph of the function y 2 x 3 1 reflect across the x axis compress by a factor of 2 translate 3 units up translated 3 units right translated 1 unit up Choose Choose Choose Choose Choose
Algebra
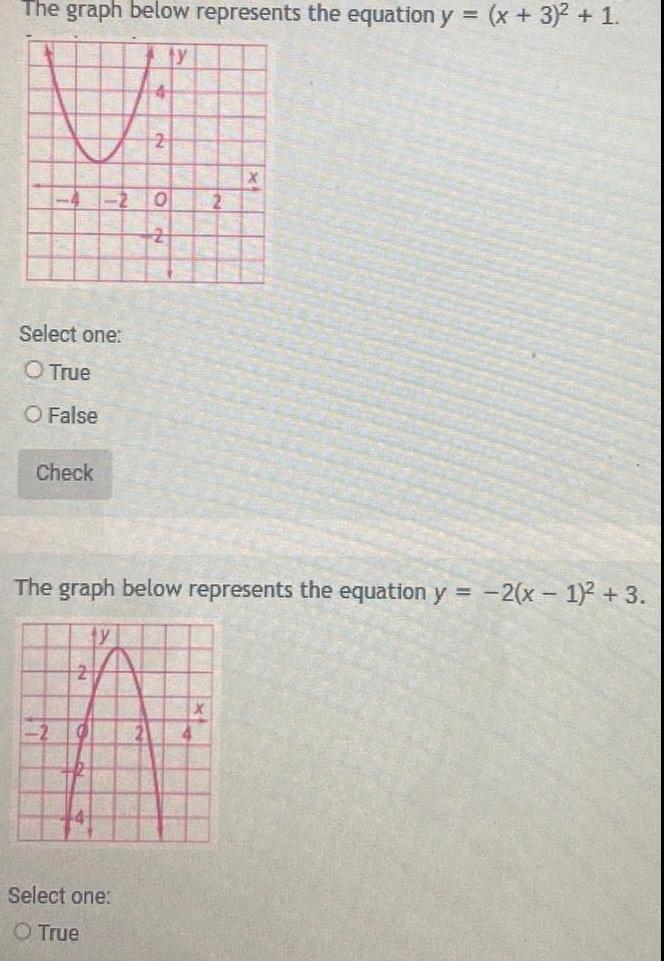
Quadratic equationsThe graph below represents the equation y x 3 1 ty 4 Select one O True O False Check 2 2 2 O 2 2 Select one O True 0 The graph below represents the equation y 2 x 1 3 2 X
Algebra
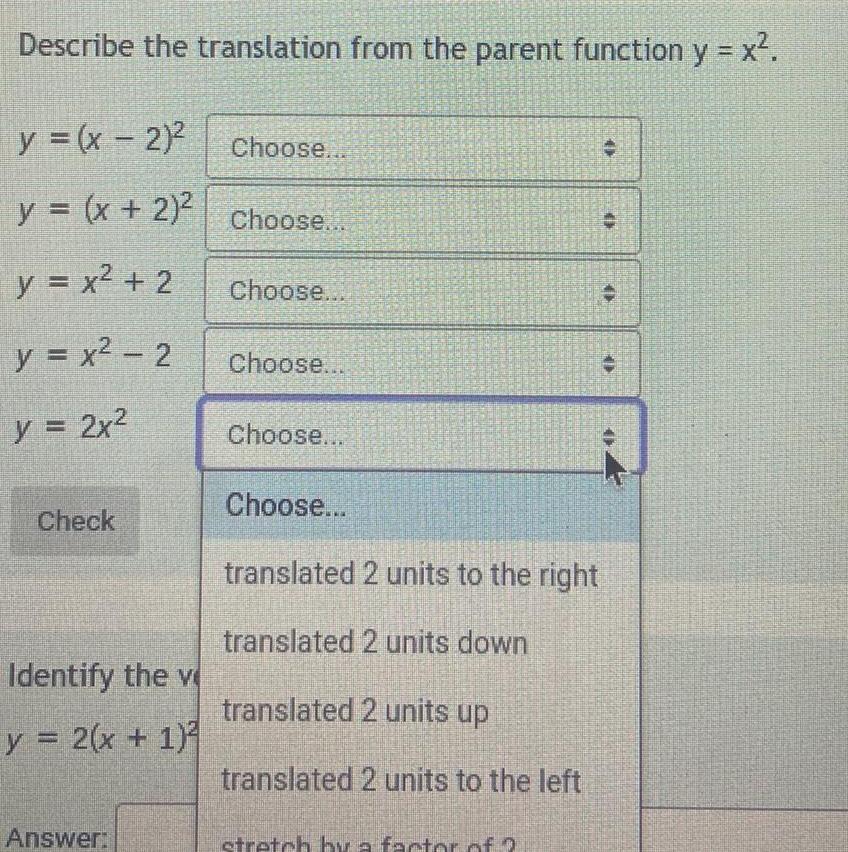
Quadratic equationsDescribe the translation from the parent function y x y x 2 Choose y x 2 y x 2 y x 2 y 2x Check Identify the v y 2 x 1 Answer Choose Choose Choose Choose Choose translated 2 units to the right translated 2 units down translated 2 units up translated 2 units to the left stretch by a factor of 2 47 ED
Algebra
Quadratic equationsAnswer Check Identify the axis of symmetry Write as the equation of a line y 2 x 1 1 Answer Check Identify the maximum or minimum y 2 x 1 1 Select one O a maximum 1 O b maximum 1
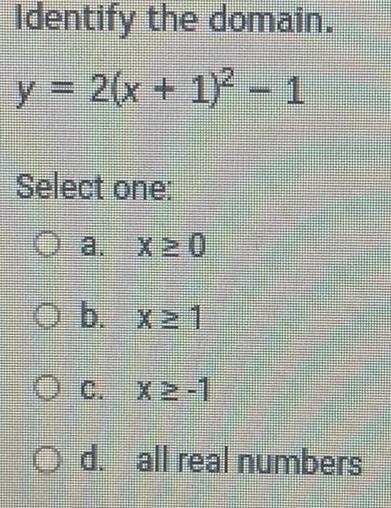
Algebra
Matrices & DeterminantsIdentify the domain y 2 x 1 2 1 Select one O a x 20 O b x 21 O c x2 1 O d all real numbers

Algebra
Quadratic equationsUse synthetic division to show that x is a solution of the equation and use the result to factor the polynomia x 28x48 0 x 4 I
Algebra
Complex numbersThe acceleration due to gravity is The acceleration due to gravity is meters per second feet per second

Algebra
Quadratic equations3 Find the factored form Use imaginary numbers to write as the product of two binomials 4b 1
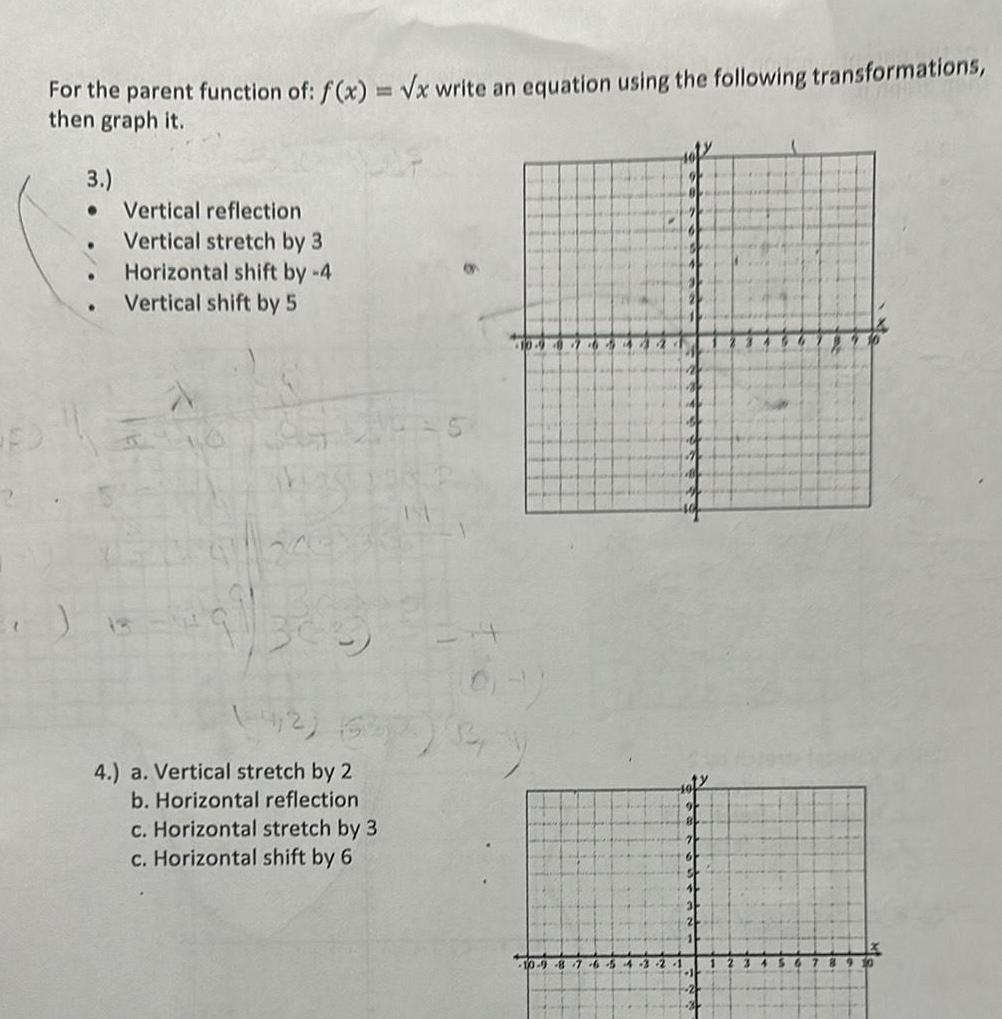
Algebra
Quadratic equationsFor the parent function of f x x write an equation using the following transformations then graph it 3 Vertical reflection Vertical stretch by 3 Horizontal shift by 4 Vertical shift by 5 4 2 4 a Vertical stretch by 2 b Horizontal reflection c Horizontal stretch by 3 c Horizontal shift by 6 11 10 4 10 9 8 7 6 54 2

Algebra
Quadratic equationsSolve using the quadratic formula Only need to input the final answer Leave in radical form when applicable a 3x 36 0 b x 14x 53
Algebra
Quadratic equationsSelect one O a 5 71 24 O b 1 4 2 3 c 2 3 O d 1 4 2 3 Check the exact X A AVAN 5X Solve using the quadratic formula Input answers from least to greatest x 25 0

Algebra
Permutations and Combinations2 Show steps to solve by Completing the Square Use fractions not decimals when applicable Other methods will not earn credit a x 13x 36 0 b x 4x 13 0

Algebra
Complex numbersUse the quadratic formula to find the exact solution s for x 3x3 0 b 3 21 2 3 21 2 3 3 2 3 3 2 c d Select one O a O b O c Od

Algebra
Quadratic equationsConsider the polynomial below Find f 2 by using synthetic division and the Remainder Theorem and by evaluating f 2 directly Use Remainder Theorem f 2 f x 2x 2x x 4 Evaluate Directly f 2

Algebra
Quadratic equations4 Use a calculator to graph and solve If exact roots cannot be found approximate to the nearest hundredth x 2x 2 0 5 Use the formula h t 1622 vt ho Melia throws a softball with an initial velocity of 32 feet per second She releases the ball at about 4 feet above the ground How long it take for the ball to reach the ground Round to the nearest tenth Show steps or explain how you found the answer 6 Write a quadratic equation and solve to find two real numbers such that their sum is 8 and their product is 209 Show or describe steps

Algebra
Matrices & Determinants4 The height of a firework at a 4th of July celebration can be modeled by a quadratic function Suppose the firework is launched from a platform thre feet off the ground at a velocity of 96 feet per second Use h t 16t vt ho a Write a function to represent the situation b Show steps to find the vertex and describe its meaning in context
Algebra
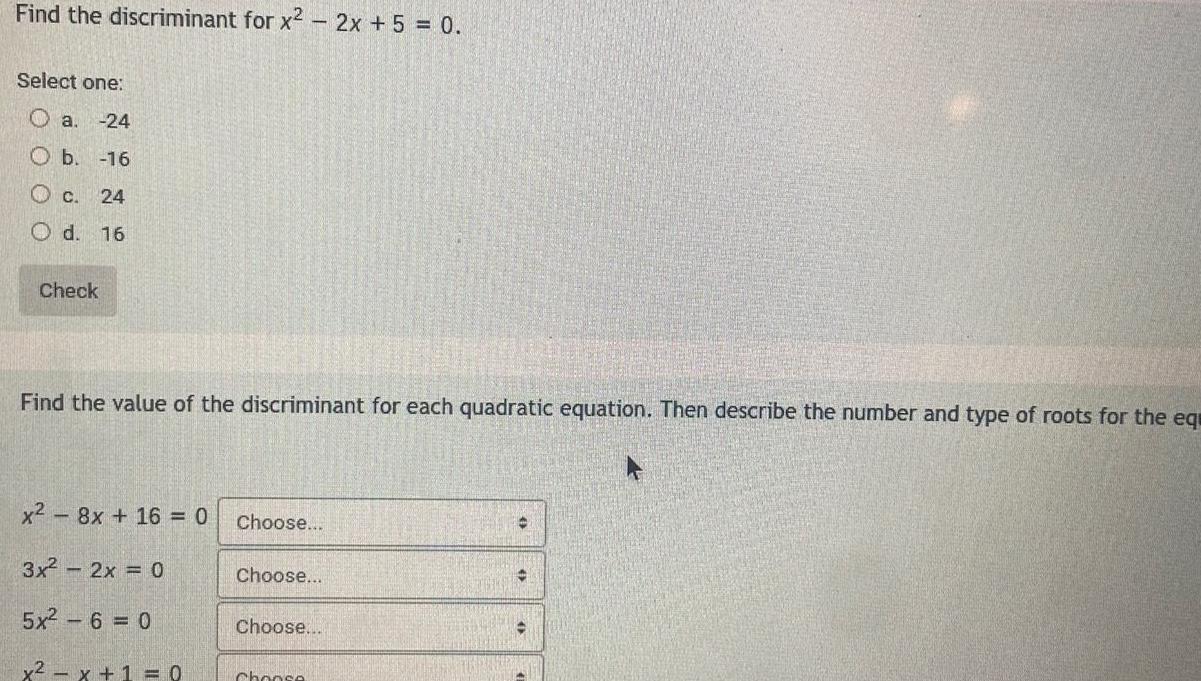
Quadratic equationsFind the discriminant for x 2x 5 0 Select one a 24 O b 16 c 24 O d 16 Check Find the value of the discriminant for each quadratic equation Then describe the number and type of roots for the eq x 8x 16 0 Choose 3x 2x 0 5x2 6 0 x x 1 0 Choose Choose Choose
Algebra
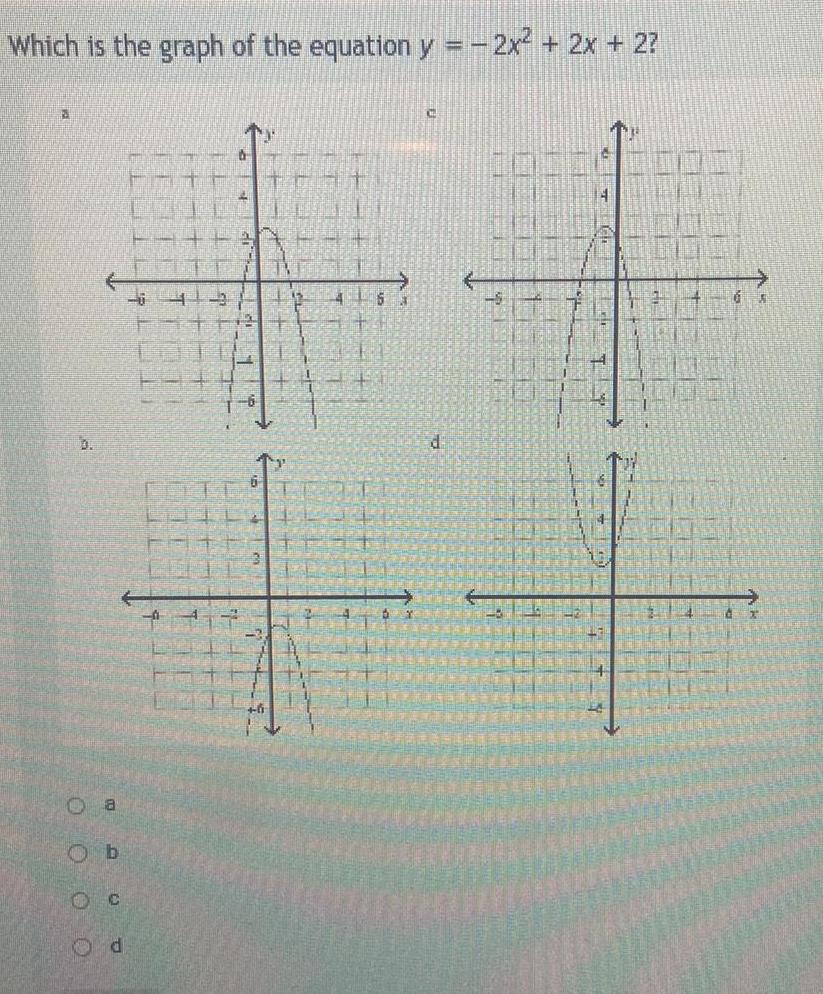
Quadratic equationsWhich is the graph of the equation y 0 0 0 0 a Ob C Od T a IL 4 2 3 1 4 6 2x 2x 2 d 4 DETT

Algebra
Quadratic equations3 y x 2x 5 a Write the function in vertex form b Find the axis of symmetry and vertex c Is the vertex a maximum or minimum How do you know
Algebra
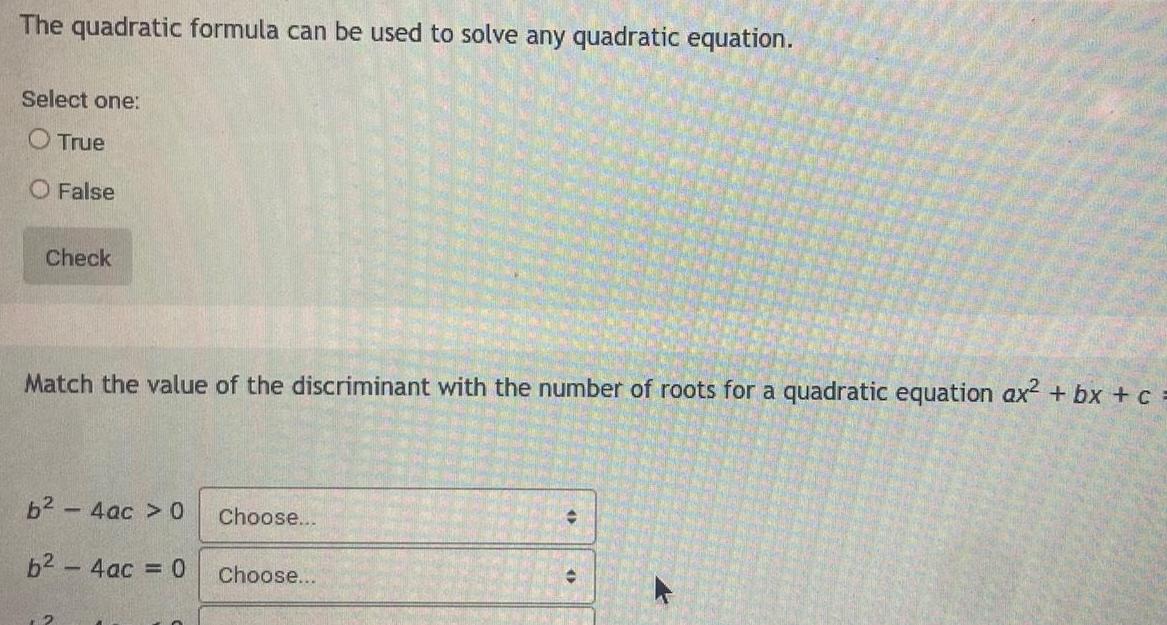
Quadratic equationsThe quadratic formula can be used to solve any quadratic equation Select one True O False Check Match the value of the discriminant with the number of roots for a quadratic equation ax bx c b 4ac 0 6 4ac 0 Choose Choose C

Algebra
Quadratic equations1 Show steps to solve each equation by the Square Root Property Other methods will not earn credit a 36x 12x 1 b 2x 20x 50 128 18

Algebra
Complex numbers1 Describe how to simplify i 2 Write the quotient as a complex number rationalize the denominator Show steps b 7 13i 21 1 i dkry 4 i 2 4 iv 2 3 Find the factored form Use imaginary numbers to write as the product of two binomials
Algebra
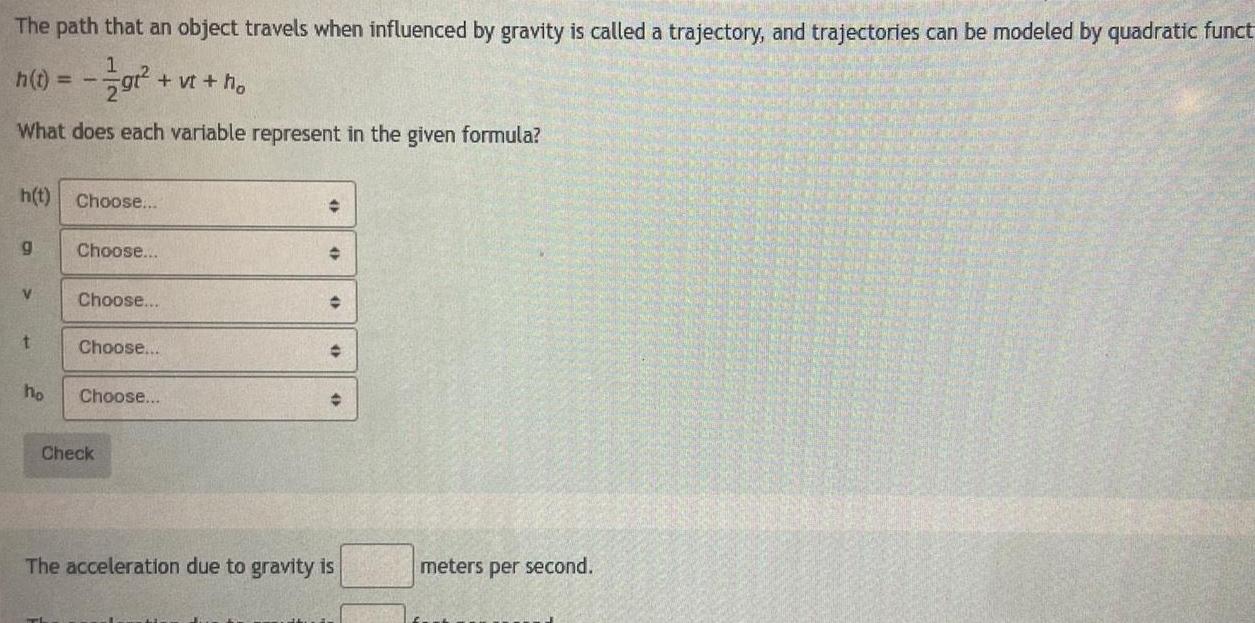
Quadratic equationsThe path that an object travels when influenced by gravity is called a trajectory and trajectories can be modeled by quadratic funct h t gt vt ho What does each variable represent in the given formula h t Choose g V t ho Choose Choose Choose Choose Check The acceleration due to gravity is meters per second
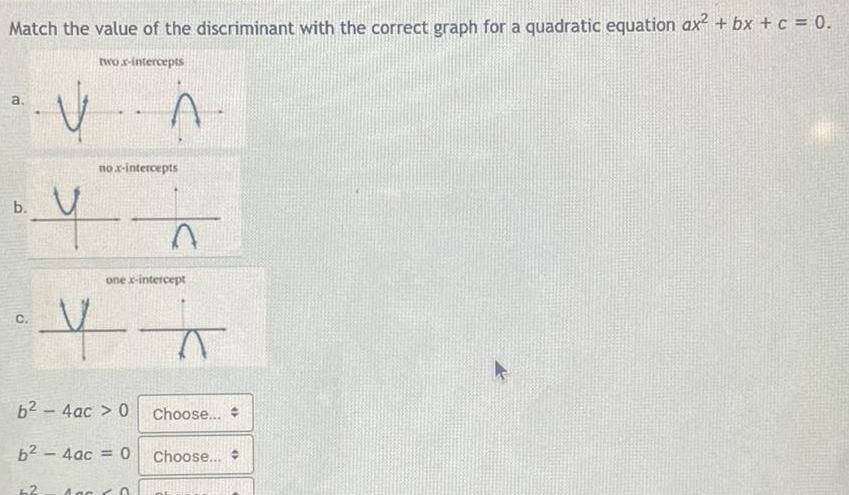
Algebra
Complex numbersMatch the value of the discriminant with the correct graph for a quadratic equation ax bx c 0 two x intercepts a b C V no x intercepts y A one x intercept 4 6 4ac 0 Choose b 4ac 0 Choose Age 0
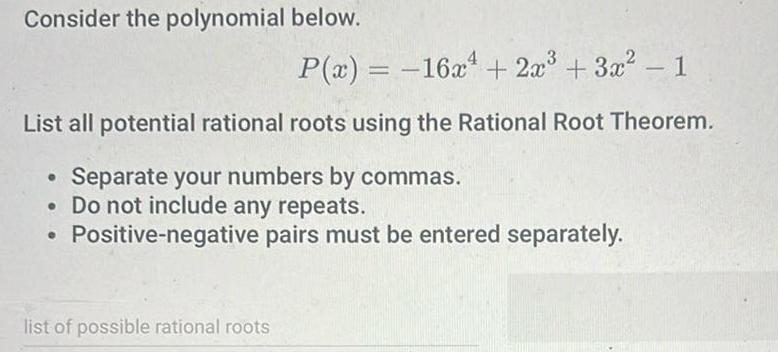
Algebra
Complex numbersConsider the polynomial below P x 16x 2x 3x 1 List all potential rational roots using the Rational Root Theorem Separate your numbers by commas Do not include any repeats Positive negative pairs must be entered separately list of possible rational roots
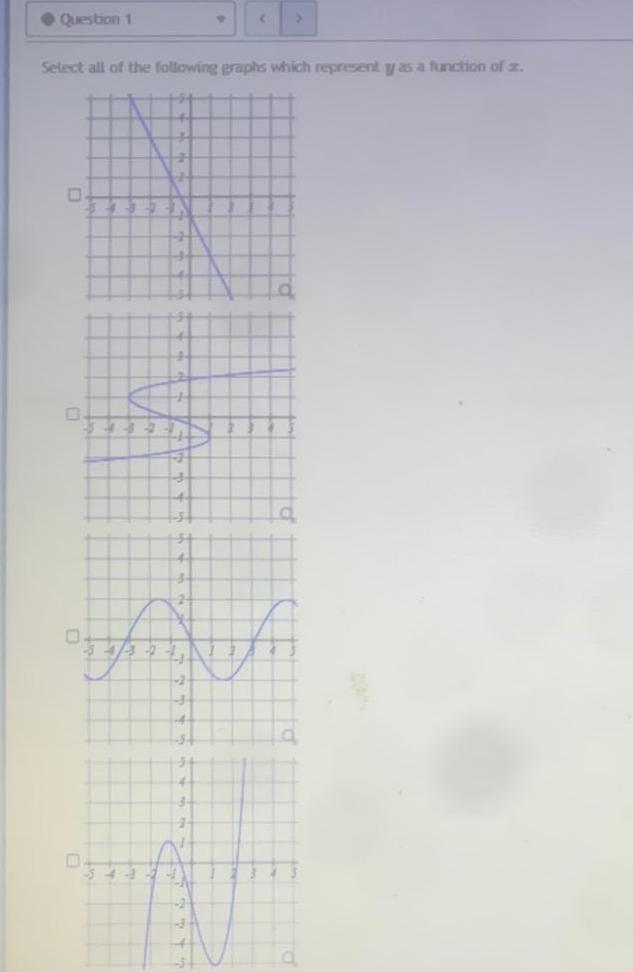
Algebra
Complex numbersQuestion 1 0 Select all of the following graphs which represent y as a function of z 50 2 54 CH T 1 a
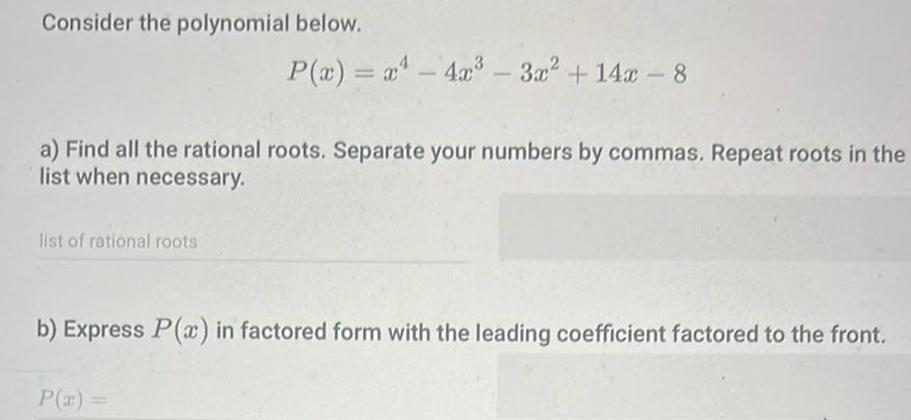
Algebra
Quadratic equationsConsider the polynomial below a Find all the rational roots Separate your numbers by commas Repeat roots in the list when necessary list of rational roots P x x 4x 3x 14x 8 b Express P x in factored form with the leading coefficient factored to the front P x

Algebra
Quadratic equations4x 28x 49 5 Input answers as decimals rounded to the nearest hundredth least to greatest X

Algebra
Quadratic equationsRewrite the equation in vertex form by completing the square Then determine the vertex Input vertex x y or y x 4x 1
Algebra
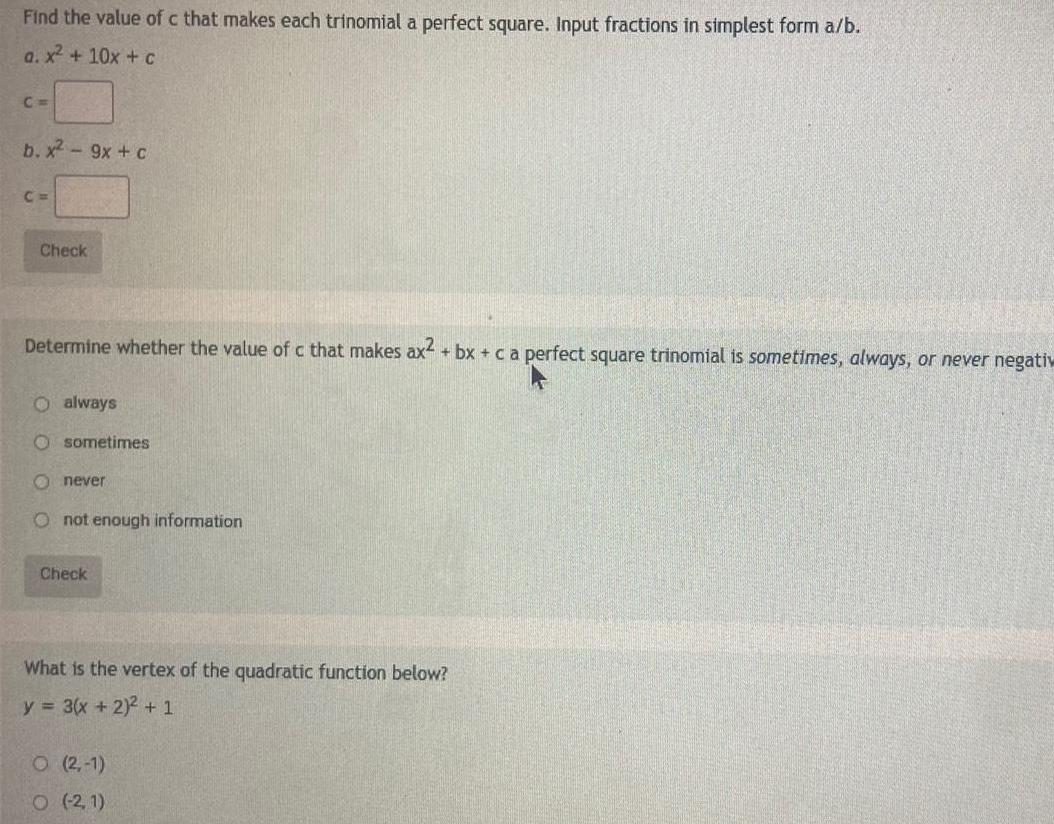
Quadratic equationsFind the value of c that makes each trinomial a perfect square Input fractions in simplest form a b a x 10x c C b x 9x c C Check Determine whether the value of c that makes ax2 bx c a perfect square trinomial is sometimes always or never negativ O always O sometimes Onever O not enough information Check What is the vertex of the quadratic function below y 3 x 2 2 1 O 2 1 O 2 1

Algebra
Quadratic equationsSolve by completing the square 3x 7x 5 9 b Oa Ob Od 7 6 3 109 6 109 3 d 7 t 3 m 10 3