Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
Application of derivativesThe current toll for the use of a certain toll road is 2 75 A study conducted by the state highway department determined that with a toll of p dollars q cars will use the road each day where q 60 000e 0 4p Is demand elastic or inelastic at p 2 75 To determine if demand is elastic or inelastic the elasticity must be computed To compute the elasticity of demand for the given equation use the formula for elasticity What is the formula for elasticity pf p OA E p f p O OC E p B E p pf p f p D E p pf p f p pf p f p 0 4p Notice that f p q 60 000e is given in the problem statement but f p is not Calculate f p 60 000e 0 4p d f p


Calculus
Differential equations8 A spotlight on the ground shines on a wall 12 m away If a man 2 m tall walks from the spotlight toward the building at a speed of 1 6 m s how fast is the length of his shadow on the building decreasing when he is 4 m from the building

Calculus
Application of derivativesFind a center of mass of a thin plate of density 8 6 bounded by the lines y x and x 0 and the parabola y 2 x in the first quadrant x 0 y 0 Type simplified fractions

Calculus
Application of derivativesSuppose that f x 3x 1 and g x 2x 9 a Solve f x 0 c Solve f x g x b Solve f x 0 d Solve f x g x e Graph y f x and y g x and find the point that represents the solution to the equation f x g x a For what value of x does f x 0 1 3 Type an integer or a simplified fraction b For which values of x is f x 0 X Type your answer in interval notation Use integers or fractions for any numbers in the expression c For what value of x does f x g x x 2 Type an integer or a simplified fraction d For which values of x is f x g x

Calculus
Differentiation4 If a snowball melts so that its surface area decreases at a rate of 1 cm min find the rate at which the diameter decreases when the diameter is 10 cm

Calculus
Application of derivatives5 The radius of a spherical ball is increasing at a rate of 2 cm min At what rate is the surface area of the ball increas ing when the radius is 8 cm


Calculus
Vector Calculusdirection that is 165 counterclockwise from the x axis Part A Find the x component of this vector Express your answer in meters View Available Hint s Hint 2 Simplify expression for the horizontal component Hint 1 How to approach the problem Tx A O Submit Request Answer wwwww

Calculus
Differentiation3 Each side of a square is increasing at a rate of 6 cm s At what rate is the area of the square increasing when the area of the square is 16 cm

Calculus
Vector CalculusDraw a propane 1 ol b heptane 2 ol c Ethanol d Diethyl ether e dipropyl ether f methyl ethyl ether


Calculus
Vector Calculus3 Draw the following a Ethanal b Propanal C Pentanal All of question d Hexane 2 one e Octane 3 one f Decane 5 one

Calculus
DifferentiationEvaluate each function ANSWER SHOULD BE A FRACTION OR MIXED NUMBER ANSWERS GIVEN AS A DECINMAL WILL BE COUNTED AS INCORRECT 5 f x 2 Find f 6 4 3 3

Calculus
Limits & ContinuityFor each of those 4 values below answer the following questions a Does the limit exist if yes the value b What type of discontinuity is it 11 Examine the graph below and answer the questions that follow assume a scale of 1 paying attention to the values where a discontinuity occurs C4 x 8 a b x 1 2 a b 1x 2 a b x 2

Calculus
Vector Calculus2 Which of the following has a point discontinuity c y x a y X b y x 1 X d y x 1 x 1

Calculus
Vector Calculus7 The height of an object thrown from a cliff is modeled by h t 4 91 3 6t 63 where tis time in seconds and h t is height in metres a What is the average velocity from time Os to time 1s A4 b What is the instantaneous velocity of the object at 1 seconds

Calculus
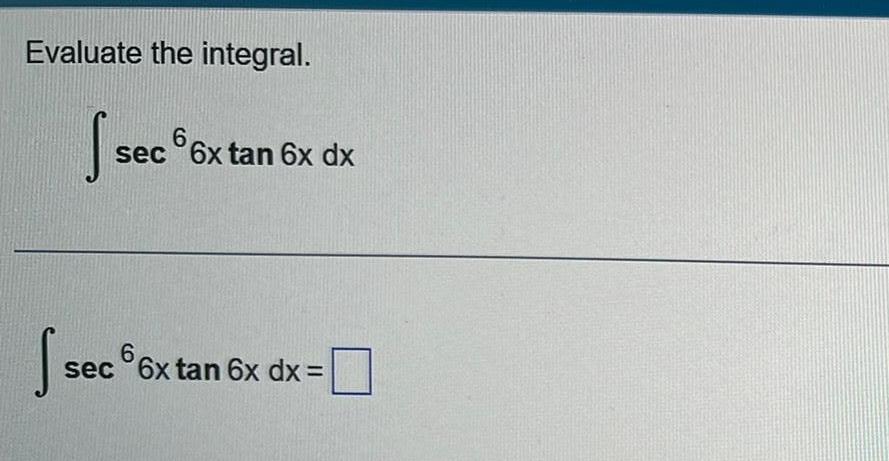
Indefinite Integration3 Determine the equation of the tangent line to the curve f x x 6 at x 10D A3

Calculus
Limits & Continuity10 The function f x is known to be continuous determine the value of a and the value of b required to make this statement true T4 6 x x 1 f x ax b 1 x 2 5x 3x 2
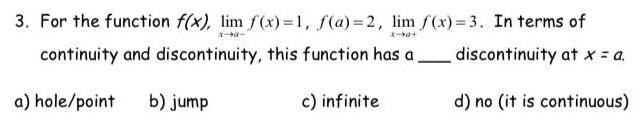
Calculus
Definite Integrals3 0 3 b0 3 For the function f x lim f x 1 f a 2 lim f x 3 In terms of continuity and discontinuity this function has a discontinuity at x a a hole point b jump c infinite d no it is continuous

Calculus
Application of derivatives6 Find the slope of the tangent at the given point f x 3 X at x 4 K3


Calculus
Limits & Continuity5 Determine if the limit exists at x 1 and if so determine the value 2x 3 x 1 f x 6 x 1 3x 2 x 1 K2


Calculus
Application of derivativesAs always show you work all relevant steps any formulas used correct use of good mathematical form and clearly indicate your answers Use skills appropriate to this chapter Circle the correct letter no work required for Multiple Choice 1 The function y has no limit at what value x 1 x 1 a x 1 b x 0 c x 1 K2 d none of the above

Calculus
Limits & ContinuityAs x f x As x 5 f x As x 5 from the right f x lim f x x 3 lim f x X 6 graph of f x below 6 What is the equation of the horizontal asymptote What is the equation of the vertical asymptote Classify the discontinuity at x 3 Classify the discontinuity at x 6

Calculus
Application of derivativesLet R be the flow rate of a gas through a cylindrical pipe for a fixed drop in pressure between the two ends of the pipe For the following recall that you do not need to simplify or expand any of your expressions a Find a formula for R r if the flow rate is proportional to the fourth power of the radius R Use k for any constant of proportionality you have in your equation 3 b If R 420 cm s in a pipe of radius 3 cm for a certain gas find a formula for the rate of flow of that gas through a pipe of radius r cm R cm s c What is the rate of flow of the same gas through a pipe with a 4 cm radius R cm s correct

Calculus
Definite Integrals2 Find a center of mass of a thin plate of density 8 6 bounded by the lines y x and x 0 and the parabola y 2 x the first quadrant x 0 y 0 Type simplified fractions

Calculus
Limits & Continuityf x I 2 kx x 1 5 3x x 1 207 If lim f x 3 and lim g x 7 find lim x 2 x 2 x2 f x 208 Find a value for k so that f x is continuous if g x


Calculus
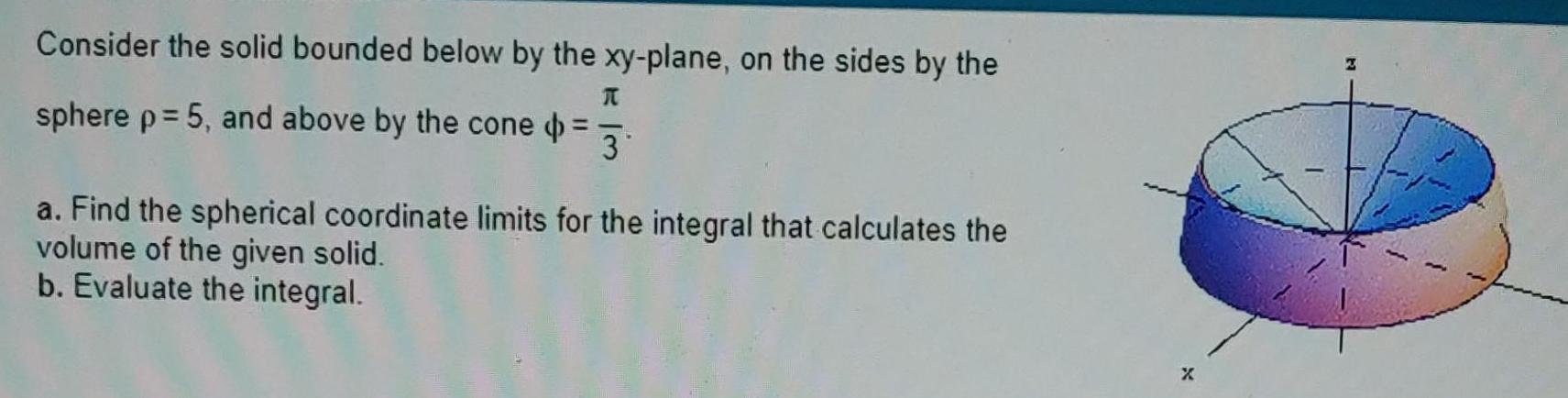
Definite IntegralsConsider the solid bounded below by the xy plane on the sides by the sphere p 5 and above by the cone 3 a Find the spherical coordinate limits for the integral that calculates the volume of the given solid b Evaluate the integral X
Calculus
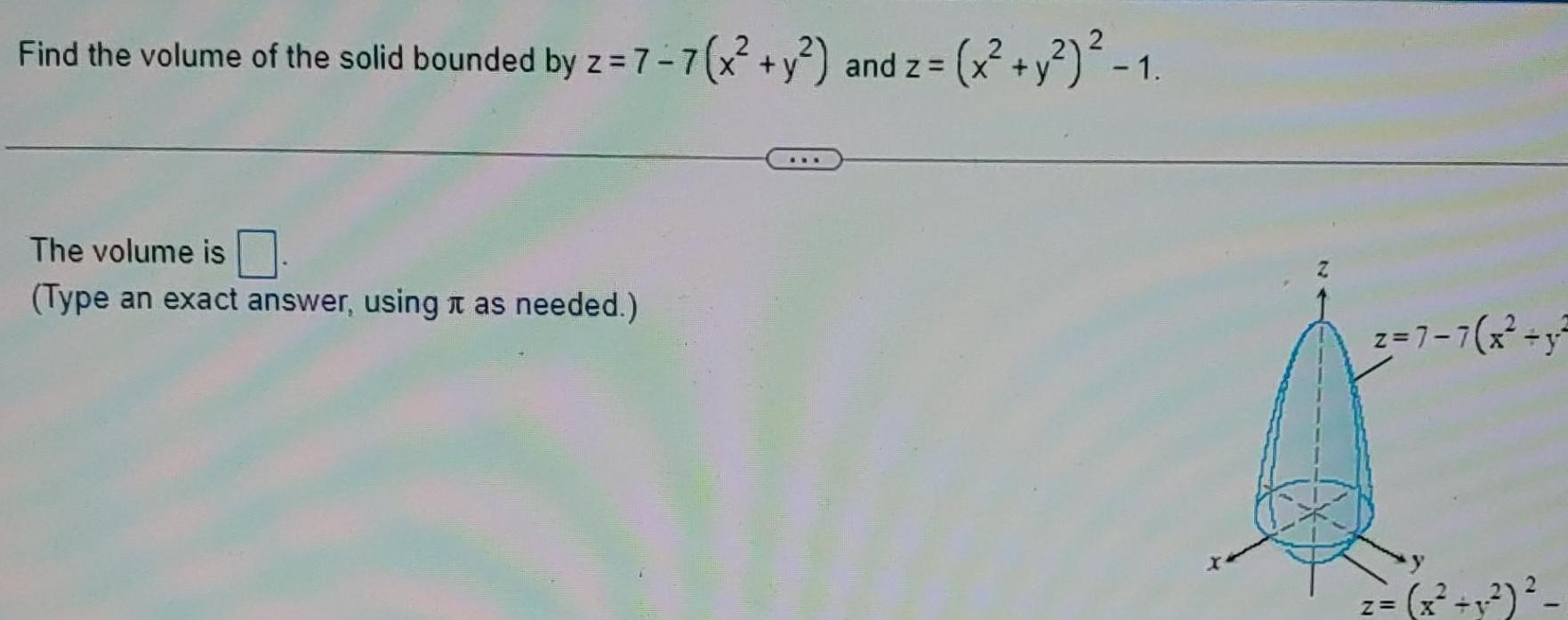
Definite IntegralsFind the volume of the solid bounded by z 7 7 x y and z 2 The volume is Type an exact answer using as needed x y 1 z 7 7 x y z x


Calculus
Limits & Continuity109 Find the average rate of change between x 2 and x 5 based on the graph below 11 10 9 6 54321 Ay y f x I 4 5 6 7 8 9 10

Calculus
Application of derivativesn 108 Suppose that the value V of a certain product depreciates with time t where V t 120 Find lim V t 30t 16 t

Calculus
Application of derivativesFiven the polynomial identify the coefficients and degree of each term 3x 2 7x 3x 4x First term degree Second term degree Third term coefficient 3 coefficient 2 degree 2 Fourth term degree 4 Fifth term degree 3 coefficient 4 Note make sure that you understand the terms leading coefficient and leading term What is the leading coefficient coefficient 7 coefficient 3 What is the degree of the leading term What is the degree of the polynomial

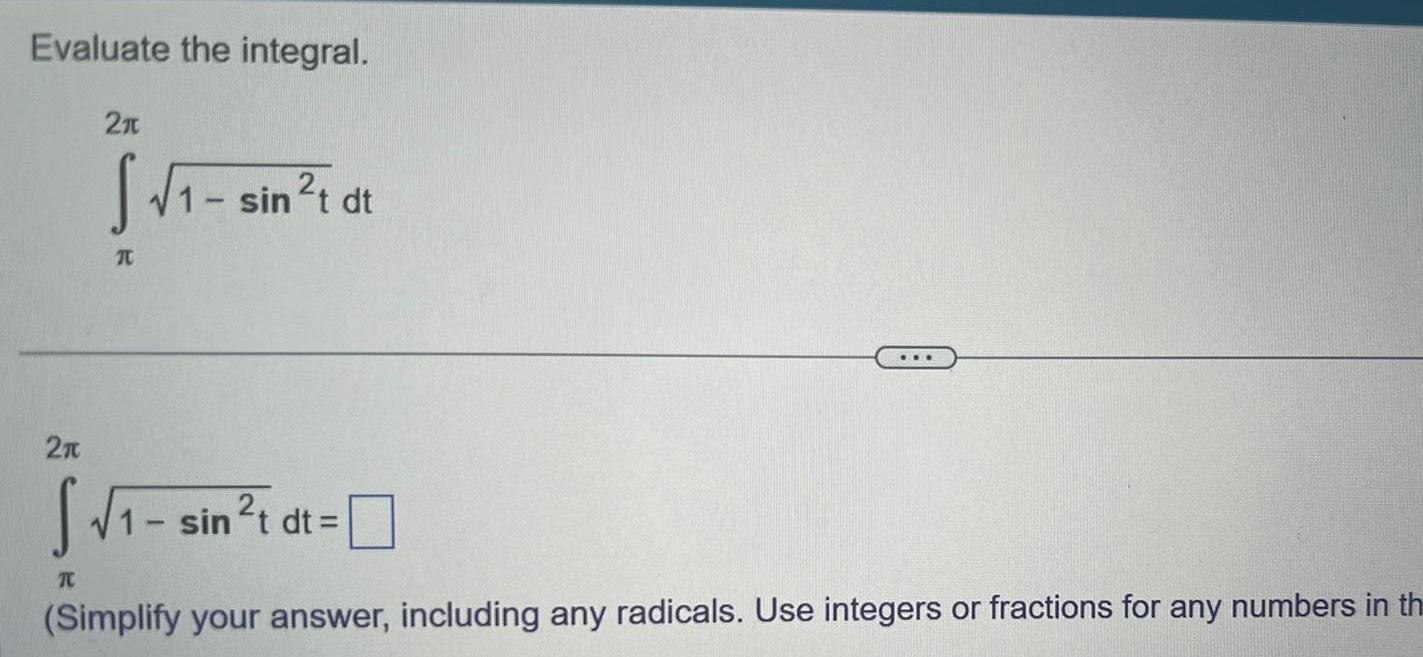
Calculus
Indefinite IntegrationEvaluate the integral 2n 21 TC S sin t dt I si sin t dt Simplify your answer including any radicals Use integers or fractions for any numbers in th


Calculus
Indefinite IntegrationSS S p sin dp do do 0 0 0 Evaluate the spherical coordinate integral The value is Type an exact answer using as needed

Calculus
Application of derivativesMath 126 Homework 9 Sects 2 7 2 8 3 12 pts a Find the inverse function of f where f x 3x 11 b Use function composition to prove that the two functions are inverses

Calculus
Application of derivativesGiven the relationship between the perimeter of a square and its side length ans a On the graph below i Construct a graph on the axes below to represent the square s perimeter P in terms of its square s side length s ii Represent an increase in the square s side length from 3 cm to 4 cm iii Represent the corresponding increase in the square s perimeter Hint 22 20 18 16 62 14 12 10 8 6 4 2 P 6 S

Calculus
Differentiation5 State the definition of the 6 Use the definition of the derivative i e the four step process to find the derivative of f x 7 4r

Calculus
DifferentiationDetermine whether the following pair of lines is parallel intersects at a single point or is skew If the lines are parallel determine whether they are the same line and thus intersect at all points If the lines intersect at a single point determine the point of intersection r 2 1 5 1 4 5 3 R 22 9 17 s 5 2 3 Select the correct choice below and if necessary fill in the answer boxes to complete your choice O A The lines intersect at the single point D Simplify your answers OB The lines are skew OC The lines are parallel OD The lines intersect at all points on the line r t

Calculus
DifferentiationSuppose the value of y and the value of a vary together at a constant rate of change so that Ay 0 5 Ax and y 1 5 when x 3 a We are given that y 1 5 when 3 Plot a point on the graph to represent these values 8 7 6 S 4 2 1 3 2 1 1 y 1 2 3 4 5 6 7 8 Clear All Draw Dot x Ax 3 75 b Suppose the value of a varies from x 3 to z 6 75 i By how much did the value of a change Preview ii By how much did the value of y change over this interval of a Ay c What is the value of y when z 6 75 Preview Enter a mathematical expression more

Calculus
Application of derivativesPractice For each problem find the required composition and state the domain of the composition f x 1 h g x 2 g h x 3 h f x 1 4x 1 x g x h x x 6 x d domars

Calculus
Indefinite IntegrationDetermine if the improper integral converges and if so evaluate it dr 8 2 Write F if the integral doesn t converge