Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
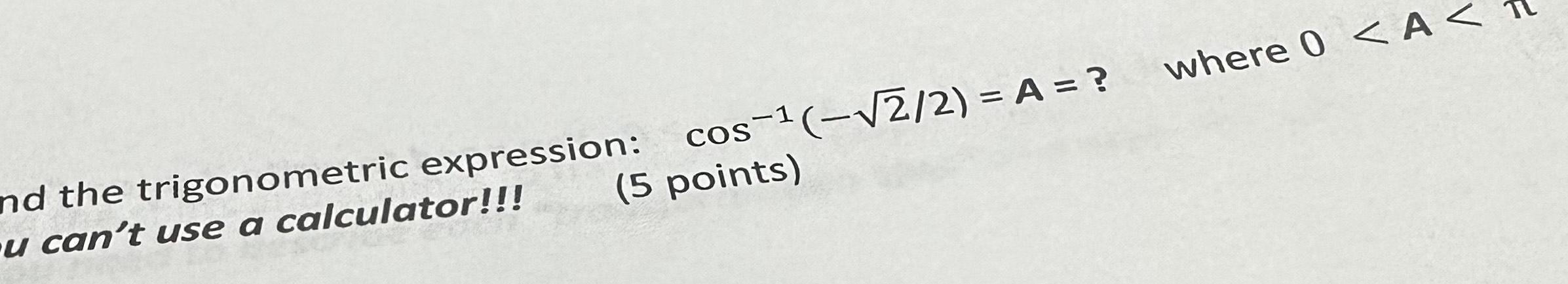
Calculus
Definite Integrals5 points and the trigonometric expression cos 2 2 A u can t use a calculator where 0 A F

Calculus
Limits & Continuity1 Use the graph of g x shown to the right to answer the following questions A lim 9 x B lim g x C lim g x 111 D miT 10touder I sio C libero om 6 A omak 1 3 2 1 y g x 1 2 g 1 Hoy of inpiroqni ai phigini la tag of vow to Host 3 4
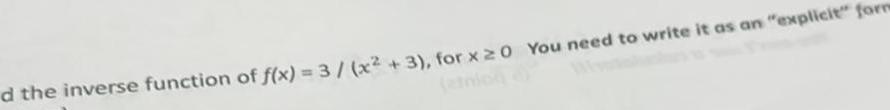
Calculus
Differentiationd the inverse function of f x 3 x 3 for x 20 You need to write it as an explicit form

Calculus
Limits & Continuityx 9 9 Given f x 7 3x A Find lim x 818 B Find lim f x 0 C Find lim f x 2 0




Calculus
Application of derivatives2 Given f x x 12 and g x x 3 5 points svin sit worb A Find fog 5 points Smotenont Find gof 5 points



Calculus
Application of derivativesWhat are the minimum and maximum values of x for which x x 6x 0 O minimum 3 maximum 0 O minimum 0 maximum 2 O minimum 3 no maximum minimum 2 no maximum
Calculus
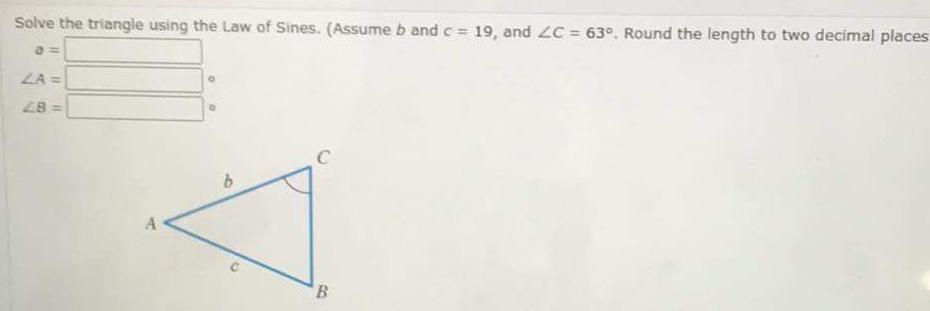
Indefinite IntegrationSolve the triangle using the Law of Sines Assume b and c 19 and ZC 63 Round the length to two decimal places a LA 28 A B

Calculus
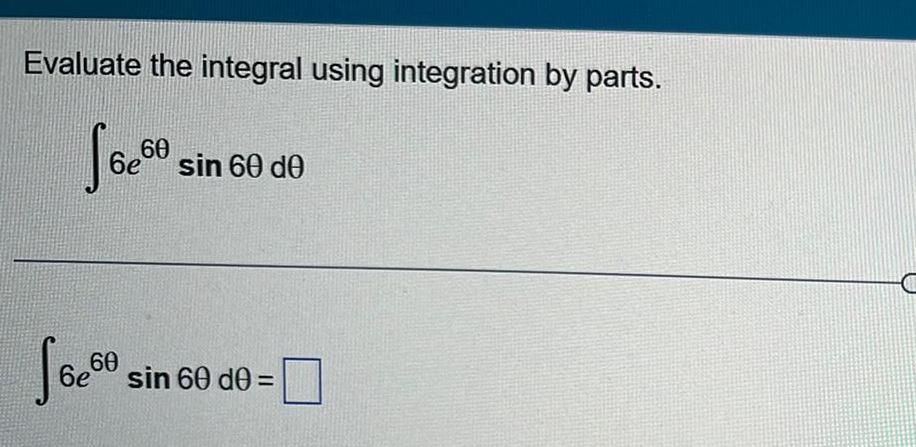
Indefinite IntegrationEvaluate the integral using integration by parts Jo 60 6e 60 6e sin 60 de sin 60 d0

Calculus
Application of derivativesEvaluate the integral by using a substitution prior to integration by parts Se 5m 5m 9 5m 9 dm
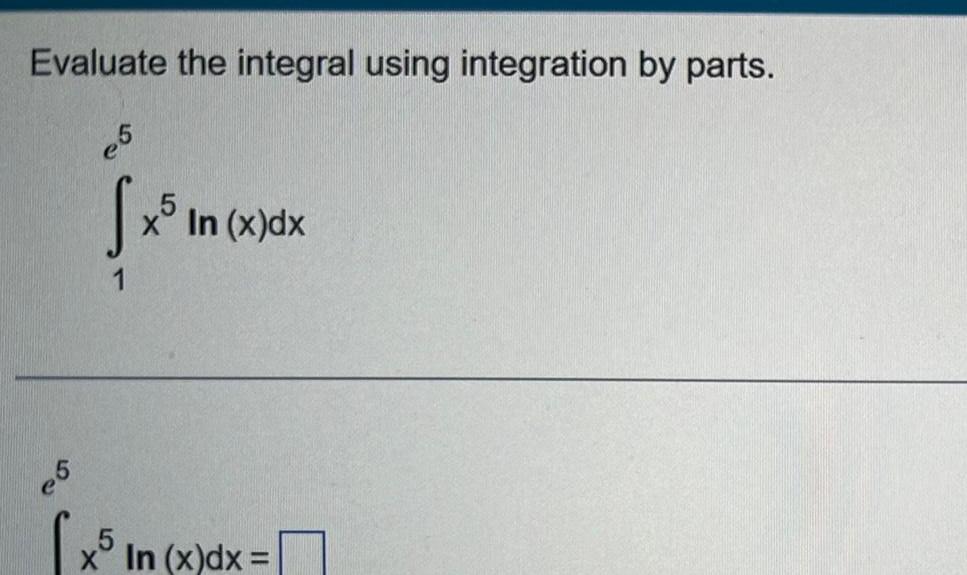
Calculus
Definite IntegralsEvaluate the integral using integration by parts e5 S x In x dx 5 x5 In x In x dx

Calculus
Application of derivativesSketch the triangle 28 32 2C 48 b 45 CH A C 45 329 B to 18 A 45 48 32 B C C 45 A 32 B 18 Solve the triangle using the Law of Sines Round side lengths to the nearest Integer a 45 32 48 A B


Calculus
Application of derivativesSolve the triangle using the Law of Sines Assume c 60 ZA 48 and 28 15 Round lengths to two decimal places x x X ZC U B

Calculus
Application of derivativesEvaluate the integral using integration by parts fxsin x dx x sin x dx



Calculus
Application of derivativesWhat is the solution of x x 9 x 1 X 3 2 1 0 3 TT 3 3 2 31 L 0 0 2 1 1 2 2 2 3 3 43 3 4 4

Calculus
Definite Integrals1 4 7 10 12 6 16 x 3sinx e C 18 tan x sec x C 440 S 4 cos cos x C 12 cos2x ax b 3a 14 20 2 tan x x 3 sec x C 22 A 17 log x 2x C MATHEMATICS 2 c x 4 x 8 C 1 m log x 1 m 2 C 5 C 2 5 9 1 15 sin 3x ax 8 at by a C 9 3x C 18 3 ax b C 7 x 2 x 2 C 3a 6 EXERCISE 7 2 4a 1 4 17 19 tan x x C 21 C 2 ax b C Rationalised 2023 24 logi x C 3 log 1 log x C cos cos 2 a ONCERT not to be republished 10 log19 4x 1 C 16 10 2log x 1 C 1 18 2 3x pe 19 log e e C

Calculus
Definite IntegralsE be the event at least two heads appear and F be the event first coin shows tail Then and Therefore and 1 Since the coins are fair we can assign the probability to each sample point Let Also with or E HHH HHT HTH THH F THH THT TTH TTT P E P HHH P HHT P HTH P THH Thus 1 1 111 Why 88 882 P F P THH P THT P TTH P TTT 408 11111 8 8 8 8 2 P EF P THH Now suppose we are given that the first coin shows tail i e F occurs then what is the probability of occurrence of E With the information of occurrence of F we are sure that the cases in which first coin does not result into a tail should not be considered while finding the probability of E This information reduces our sample space from the set S to its subset F for the event E In other words the additional information really amounts to telling us that the situation may be considered as being that of a new random experiment for which the sample space consists of all those outcomes only which are favourable to the occurrence of the event F Now the sample point of F which is favourable to event E is THH 1 Thus Probability of E considering F as the sample space 4 EnF THH 1 Probability of E given that the event F has occurred 4 This probability of the event E is called the conditional probability of E given that F has already occurred and is denoted by P EIF P EIF MATHEMATICS Note that the elements of F which favour the event E are the common elements of E and F i e the sample points of En F RT 1 P EIF Thus we can also write the conditional probability of E given that F has occurred as Number of elementary events favourable to EnF Number of elementary events which are favourable to F n EF n F Rationalised 2023 24 blished Dividing the numerator and the denominator by total number of elementary events of the sample space we see that P EIF can also be written as n EnF n S n F n S Note that 1 is valid only when P F 0 i e F Why P EIF P EF P F hed 1

Calculus
Definite Integrals1 1 4 Composition of Functions 1 Letf A B and g B C be two functions Then the composition of f and g denoted by g of is defined as the function g of AC given by go f x g y xe A ii Iff A B and g BC are one one then g of A C is also one one iii Iff A B and g BC are onto then g of AC is also onto However converse of above stated results ii and iii need not be true Moreover we have the following results in this direction iv Letf A B and g BC be the given functions such that g of Then fis one one v Letf A B and g BC be the given functions such that g is onto ER 1 1 5 Invertible Function 1 A function f X Y is defined to be invertible if there exists a function g Y X such that g of 1 and fog 1 The function g is called the inverse of fand is denoted by f ii A function f X Y is invertible if and only if f is a bijective function blated one one is onto Then i If f X Y g Y Z and h Z S are functions then ho gof hog of iv Let f X Y and g Y Z be two invertible functions Then g of is also invertible with gof fog 1 1 6 Binary Operations i A binary operation on a set A is a function AxA A We denote a b by a b ii A binary operation on the set X is called commutative if a b ba for every a be X iii A binary operation A x AA is said to be associative if a b c a b c for every a b c e A iv Given a binary operation AxAA an elemente e A if it exists is called identity for the operation if ae a e a ya A 1 2 Solved Examples Short Answer S A Example 1 Let A 0 1 2 3 and define a relation R on A as follows R 0 0 0 1 0 3 1 0 1 1 2 2 3 0 3 3 Is R reflexive symmetric transitive RELATIONS AND FUNCTIONS 3 v Given a binary operation A x AA with the identity element e in A an element a A is said to be invertible with respect to the operation if there exists an element b in A such that a b e ba and b is called the inverse of a and is denoted by a Solution R is reflexive and symmetric but not transitive since for 1 0 3 e R whereas 1 3 Example 2 For the set A 20 04 2018 R and R 11 2 3 define a relation R in the set A as follows

Calculus
Definite Integralsn F Dividing the numerator and the denominator by total number of elementary events of the sample space we see that P EIF can also be written as P EIF Also Note that 1 is valid only when P F 0 i e F Why Thus we can define the conditional probability as follows Definition 1 If E and F are two events associated with random experiment the conditional probability of the event E given that F has occurred i e P EIF is given by P EIF We have n EF n S n F n S P SIF 13 2 1 Properties of conditional probability Let E and F be events of a sample space S of an experiment then we have Property 1 P SIF P FIF 1 We know that P EF P F P FF P F P AUB IF P SOF P F P F P F provided P F 0 P FIF Thus P SIF P FIF 1 Property 2 If A and B are any two events of a sample space S and F is an event of S such that P F 0 then P AUB IF P A F P BIF P AB IF Rationalised 2023 24 P F 1 P F In particular if A and B are disjoint events then P AUB IF P A F P BIF P AUB FI P F same sample space of a Property 3 P EIF 1 P EIF From Property 1 we know that P SIF 1 P EEF 1 pride you P AF U BF P F by distributive law of union of sets over intersection P AF P BOF P AOB OF P F When A and B are disjoint events then P AB IF 0 P AB F P A F P BIF PROBABILITY 409 P AF P BF P AB FJ P F P F P F P A F P BIF P AB IF since SEVE

Calculus
Definite Integrals1 4 ax b 3a 7 10 log x 2x C 2 12 14 16 x 3sin x e C 18 tan x sec x C 6 440 20 2 tan x 3 sec x C 22 A C 8 11 4 cos cos x C 5 12 14 17 2 5 MATHEMATICS 8 log x 1 m C ONCERT not to be republished sin 3x 3 9 C 15 2 cx 4a x 4 x 8 C x c 3 EXERCISE 7 2 ax b C 7 x 2 x 2 C 3a 6 2 logixl C 3 log 1 logx C 9 1 cos 2 ax b C Rationalised 2023 24 x x 1 C 17 3 19 tan x x C 21 C 18 C 4 3cos x 10 13 log19 4x 1 C 16 10 2log x 1 C 1 18 2 3x 19 log e e C Ble te 9 C
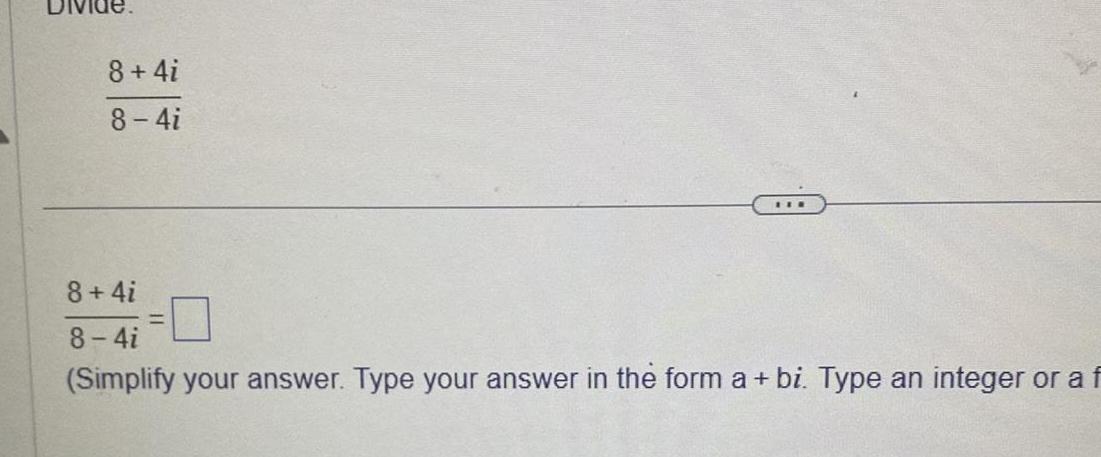
Calculus
Differentiation8 4i 8 4i TIE 8 4i 8 4i Simplify your answer Type your answer in the form a bi Type an integer or a f

Calculus
Application of derivativeshe given complex number a state the real part B state the imaginary or nonreal complex hat is the real part of 2 979 PUT part and 6 identify the num
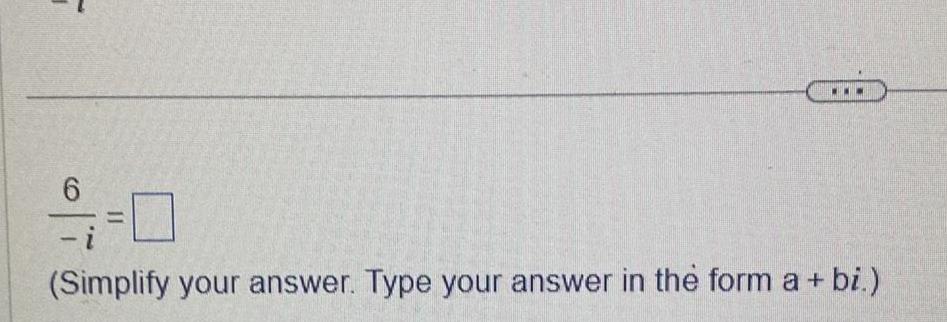

Calculus
Application of derivativesSimplify the power of i 1 22 C 1 i 22 Simplify your answer Type your answer in the form a
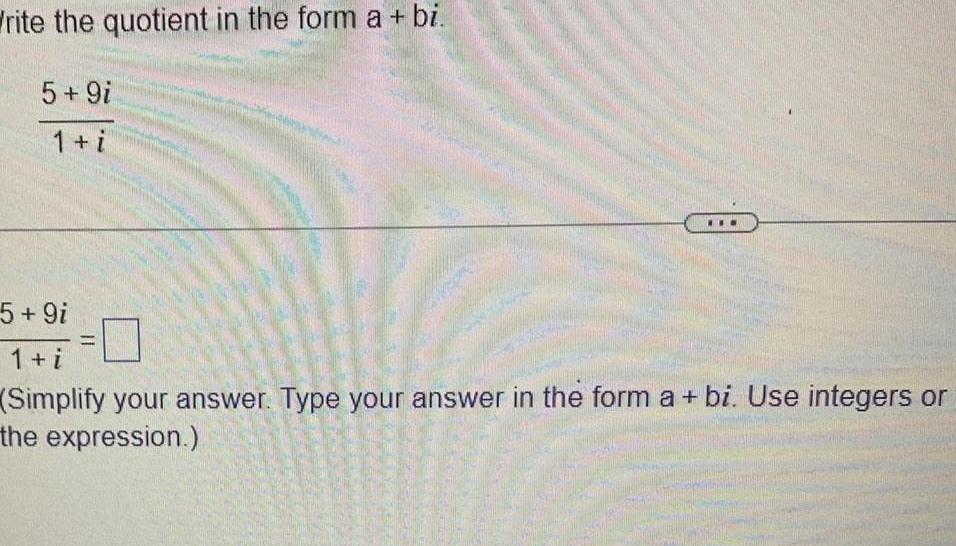
Calculus
DifferentiationWrite the quotient in the form a bi 5 9i 1 i 5 9i 1 i Simplify your answer Type your answer in the form a bi Use integers or the expression

Calculus
Application of derivativesFind the complex conjugate of the given complex number 4 2i The complex conjugate is Type an exact answer using radicals and as needed

Calculus
Application of derivativesFind the product and write the result in standard form i 6 4i 6 4i www i 6 4i 6 4i Type an integer or a simplified fraction Type your answer in the form a bi


Calculus
Application of derivatives5 4i 2 7i 5 4i 2 7i Simplify your answer Type your answer in the form a bi Do not fa

Calculus
Application of derivatives2 2 2 2 Simplify your answer Type your answer in the form a bi Type an exact answer using radicals as


Calculus
Application of derivativesuply 2 6i 2 6i Simplify your answer Type your answer in the form a bi

Calculus
DifferentiationDivide as indicated 21 3 21 3 Simplify your answer Type an exact answer using radicals and i as needed Use integers or frac numbers in the expression
Calculus
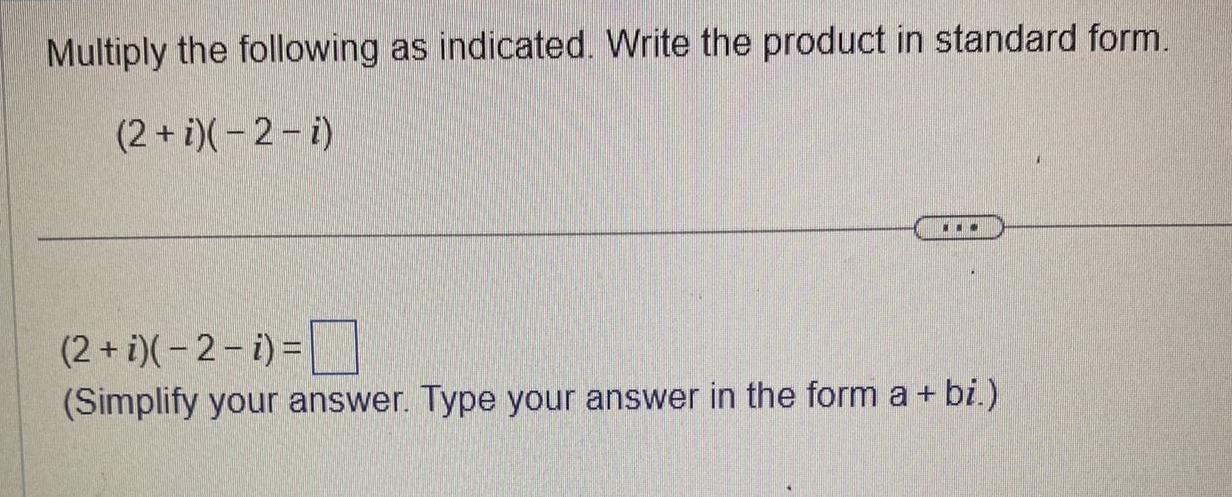
Definite IntegralsMultiply the following as indicated Write the product in standard form 2 i 2 i 2 i 2 i Simplify your answer Type your answer in the form a bi


Calculus
Application of derivativesthe following complex numbers Write the difference in star 5 9i 10i 8 9i 10i 8 Type your answer in the form a bi

Calculus
Application of derivatives8 5i 5 5i 8 5i 5 5i Simplify your answer Type your answer in the form a bi


Calculus
Application of derivativesPerform the indicated multiplication 4i 2 8i 4i 2 8i Simplify your answer Type your answer in the form a ba



Calculus
Limits & Continuity2x 2 17 Finding a symmetric interval Let f x and note x 1 that lim f x 4 For each value of e use a graphing utility to find all values of 8 0 such that f x 4 whenever 0 x 1 d a 2 b 8 1 IC c For any 0 make a conjecture about the value of 8 that sat isfies the preceding inequality