Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
Calculus
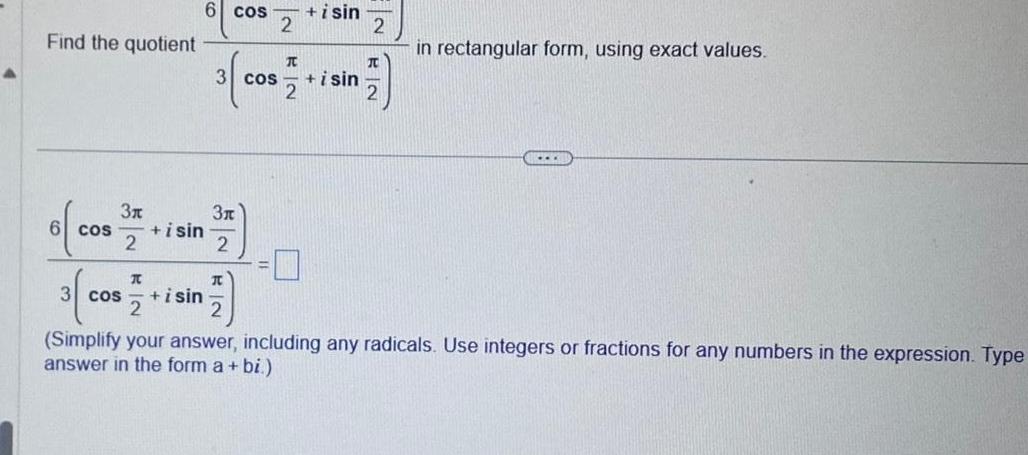
Application of derivativesFind the quotient 3x 6 cos i sin 2 T 3 3 cos i sin 2 6 cos i sin 2 3 cos 3x 2 172 I 2 i sin 2 BIN in rectangular form using exact values Simplify your answer including any radicals Use integers or fractions for any numbers in the expression Type answer in the form a bi
Calculus
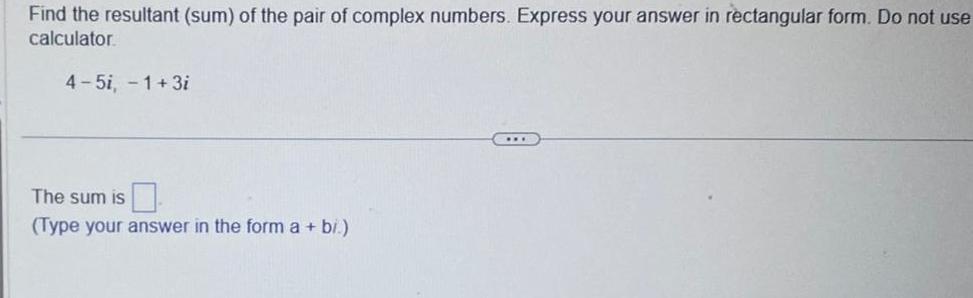
Application of derivativesFind the resultant sum of the pair of complex numbers Express your answer in rectangular form Do not use calculator 4 5i 1 3i The sum is Type your answer in the form a bi

Calculus
Differential equationsFinal Exam Practice Problems Consider the region bounded by y ln x over 1 e a Set up integrals using both methods if revolved about the z axis Repeat if revolved about the y axis Find each volume b Set up integrals if revolved about y 1 both methods c Set up an integral that computes the length of the curve d Set up an integral that computes the area if the curve is revolved about the z axi
Calculus
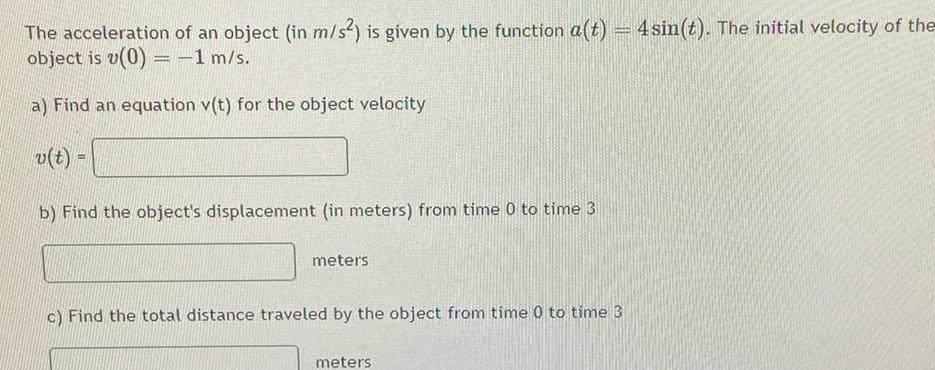
Application of derivativesThe acceleration of an object in m s is given by the function a t 4 sin t The initial velocity of the object is v 0 1 m s a Find an equation v t for the object velocity v t b Find the object s displacement in meters from time 0 to time 3 meters c Find the total distance traveled by the object from time 0 to time 3 meters

Calculus
Differential equationsUse absolute value on a graphing calculator to find the area bounded by the graphs of the equations over the given interval y e x y 0 1x 0 4 2 x 2 The area is
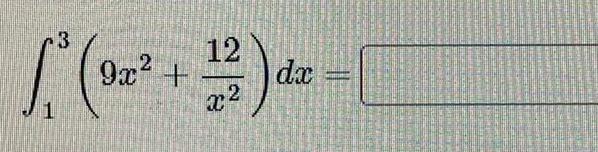

Calculus
Vector Calculus12 Vector a joins the x and y intercepts tail at the x intercept and head at the y intercept of the line 2x 3y 6 Determine a as a quadrant bearing

Calculus
Vector CalculusApplication 3 An airplane is on a heading of 030 at an airspeed of 800 km h There is a wind of 75 km h from 315 Using trigonometry find the resultant velocity as a true bearing of the airplane Include a diagram
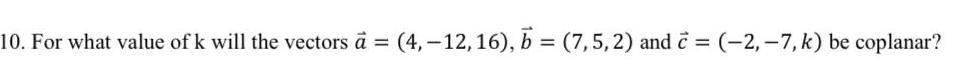
Calculus
Application of derivatives10 For what value of k will the vectors a 4 12 16 b 7 5 2 and c 2 7 k be coplanar

Calculus
Application of derivatives9 Determine the value s of z such that the points A 1 5 8 B 0 9 4 and C 8 5 z form an Isosceles triangle where AC is the base i e the non equal side
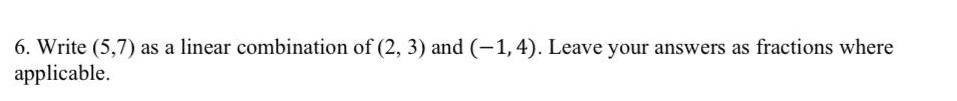
Calculus
Application of derivatives6 Write 5 7 as a linear combination of 2 3 and 1 4 Leave your answers as fractions where applicable
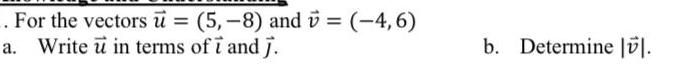
Calculus
Application of derivativesFor the vectors u 5 8 and v 4 6 a Write u in terms of i and j b Determine lvl
Calculus
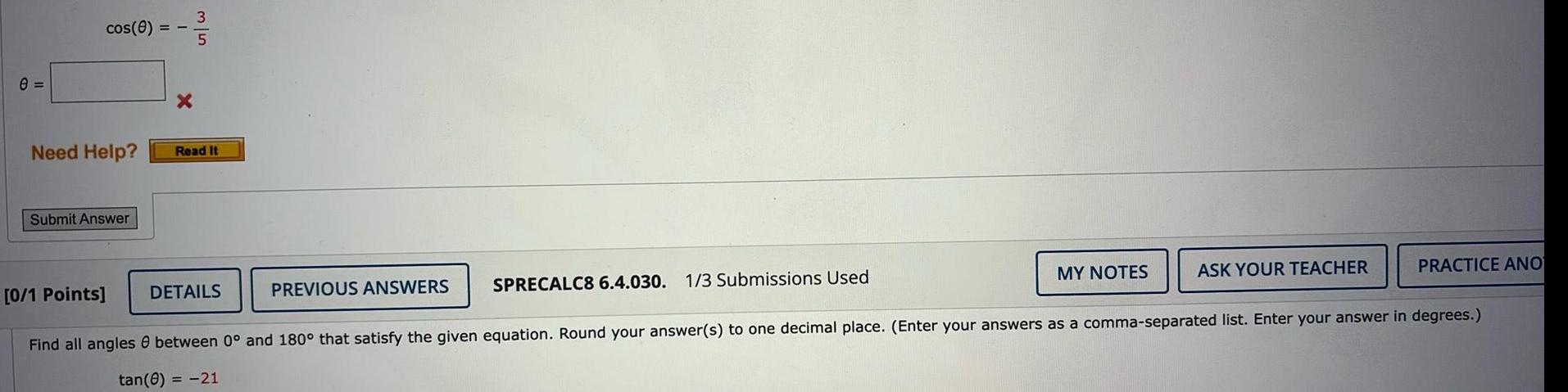
Limits & Continuitye cos 0 Need Help Submit Answer 0 1 Points X 35 Read It DETAILS PREVIOUS ANSWERS SPRECALC8 6 4 030 1 3 Submissions Used MY NOTES ASK YOUR TEACHER PRACTICE ANO Find all angles 8 between 0 and 180 that satisfy the given equation Round your answer s to one decimal place Enter your answers as a comma separated list Enter your answer in degrees tan 0 21
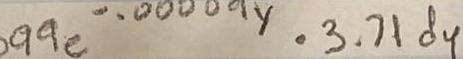
Calculus
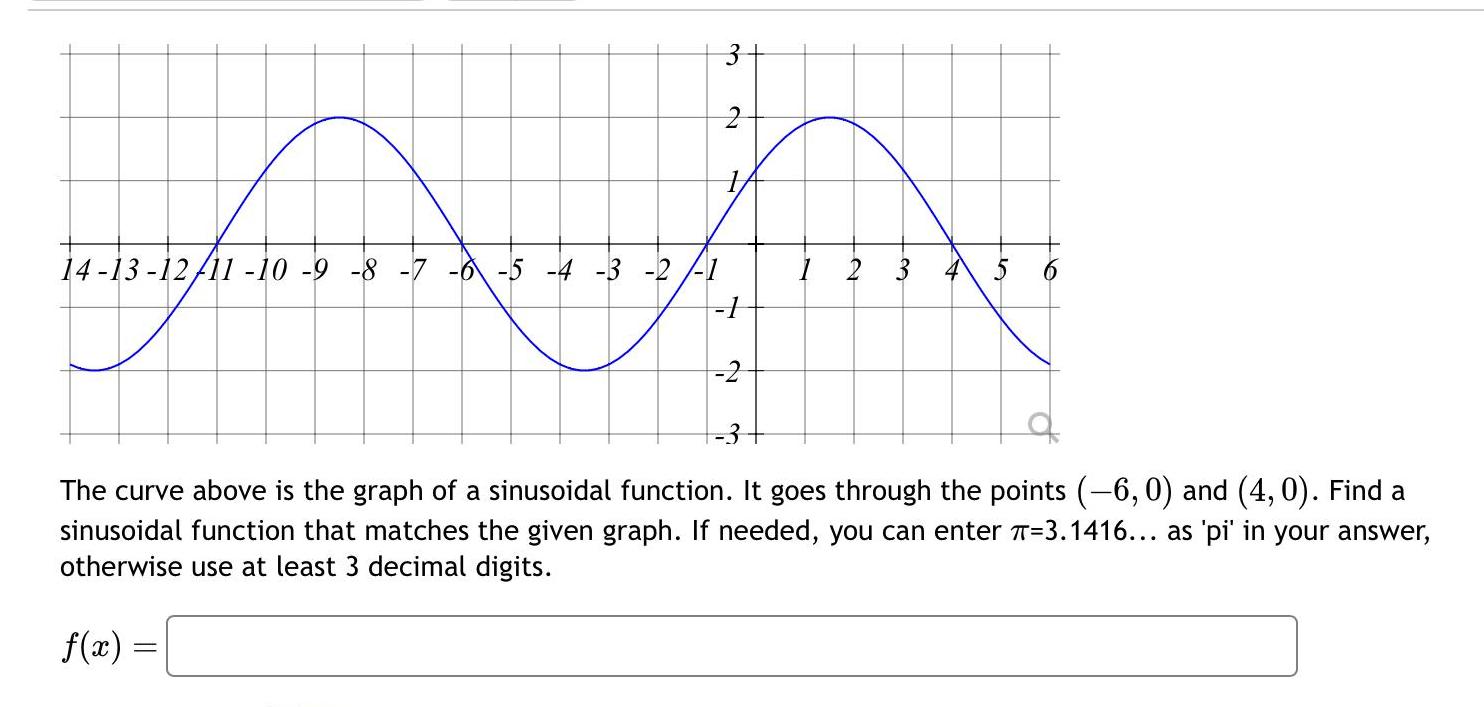
Differential equations3 2 T 14 13 12 11 10 9 8 7 6 5 4 3 2 1 1 2 3 10 The curve above is the graph of a sinusoidal function It goes through the points 6 0 and 4 0 Find a sinusoidal function that matches the given graph If needed you can enter T 3 1416 as pi in your answer otherwise use at least 3 decimal digits f x

Calculus
DifferentiationA company determined that the marginal cost C x of producing the xth unit of a product is given by C x x 4x Find the total cost function C assuming that C x is in dollars and that fixed costs are 6000 C x CO

Calculus
Indefinite IntegrationFind s t where s t represents the position function v t represents the velocity function and a t represents the acceleration function a t 301 6 with v 0 5 and s 0 8
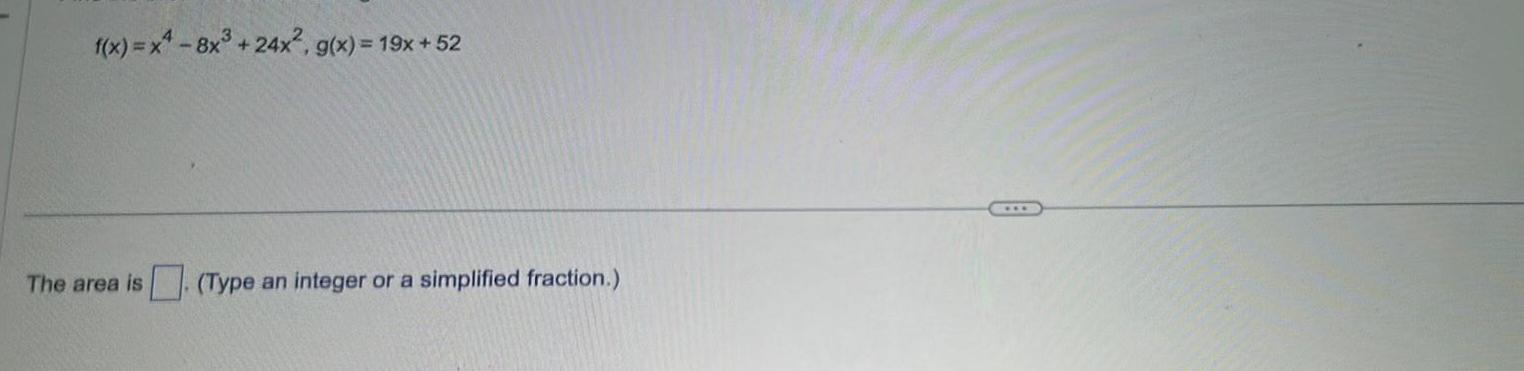

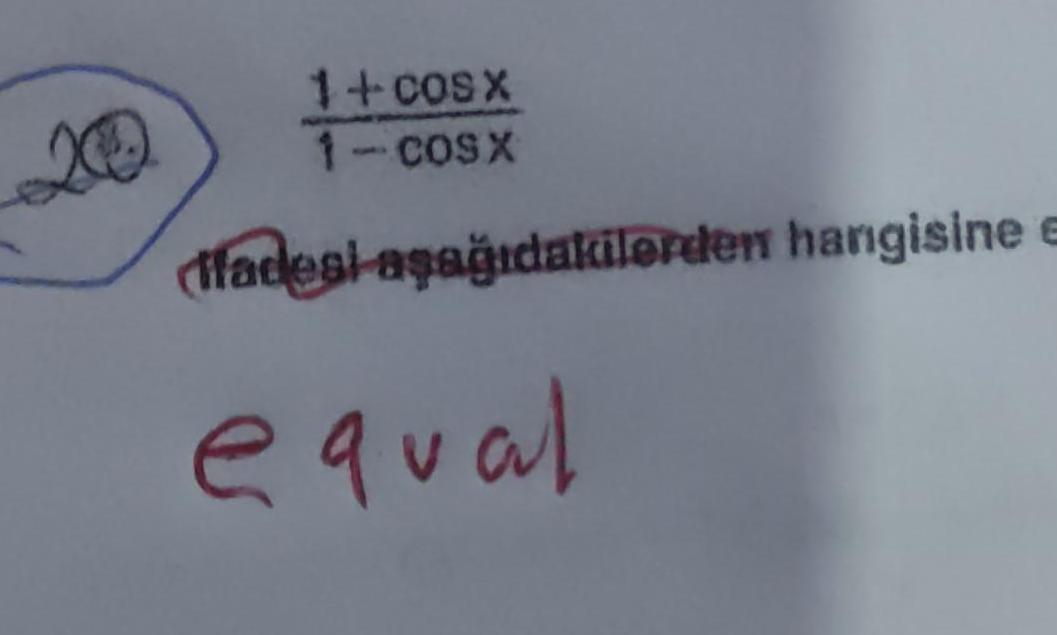
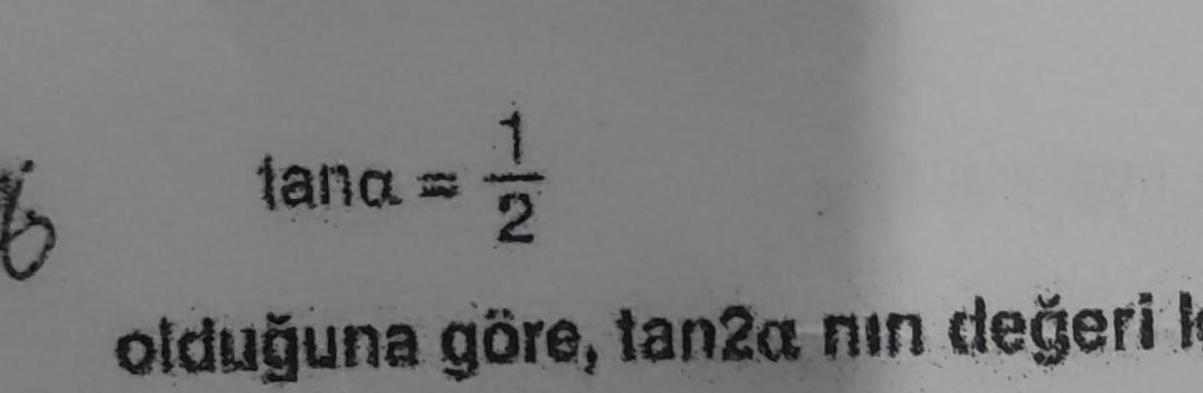

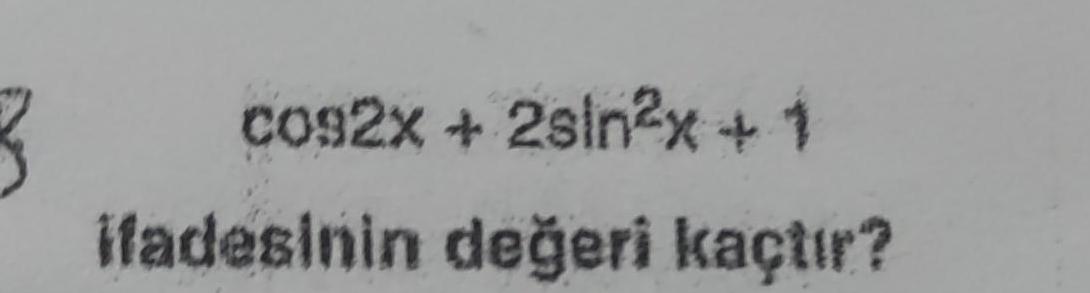


Calculus
Application of derivatives6 log 8 log 7 log 9 I leminin sonucu ka t r What is the result of The transaction

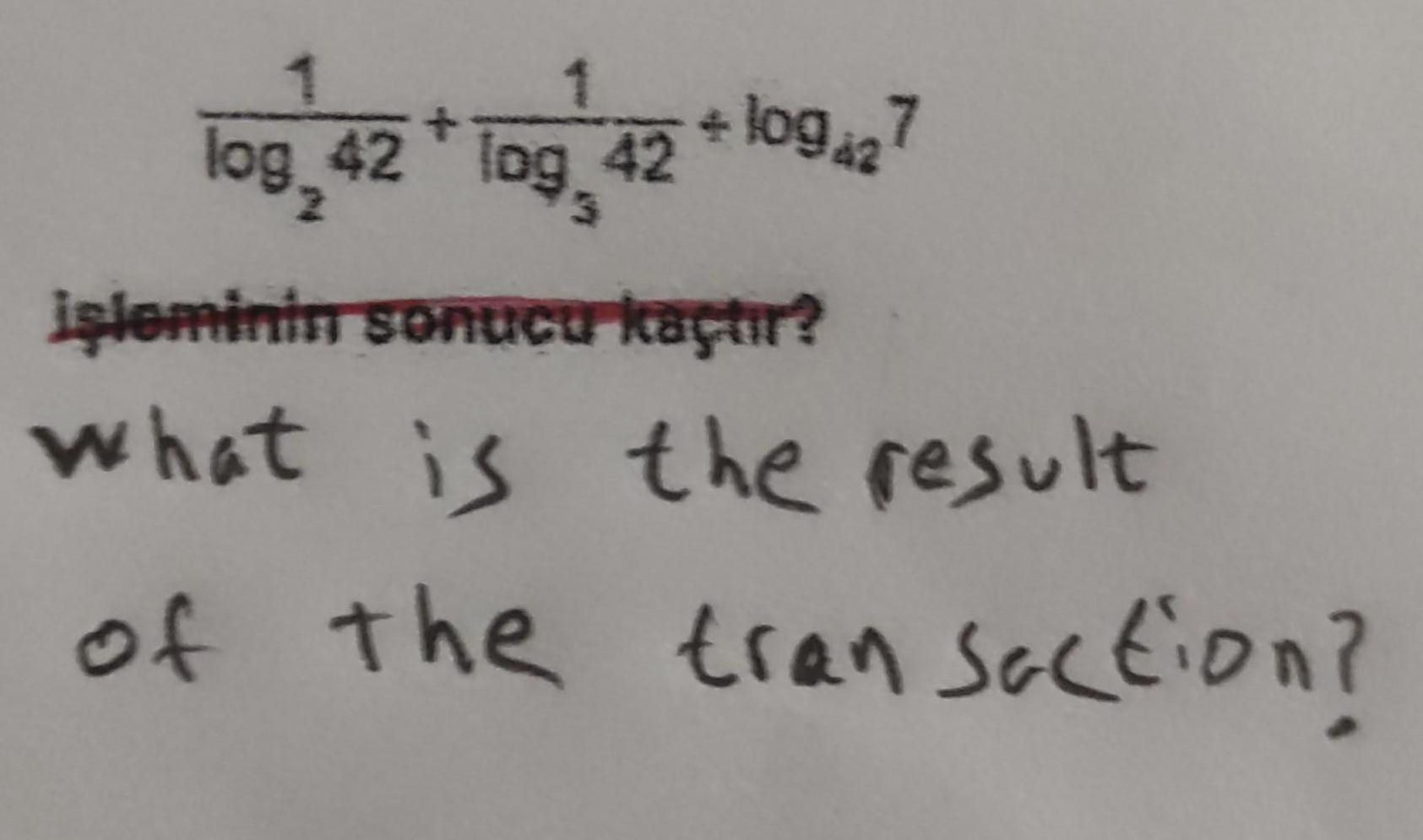
Calculus
Application of derivatives1 log 42 log 42 log427 i leminin sonucu ka t r what is the result of the transaction
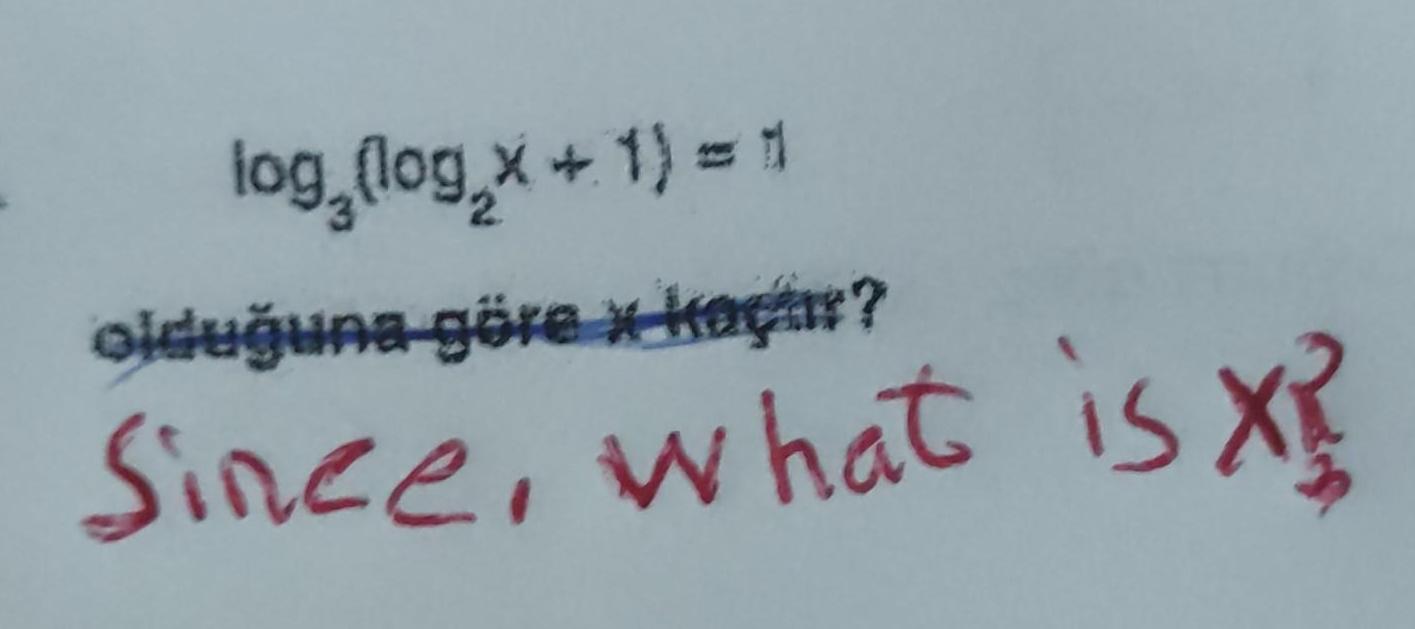

Calculus
Definite IntegralsFind the area bounded by the graphs of the indicated equations over the given interval when stated Compute answers to three decimal places y x 3 y 6x 6 1 x 2 The area calculated to three decimal places is ACTOR square units

Calculus
Definite IntegralsFind the area bounded by the graphs of the indicated equations over the given interval when stated Compute answers to three decimal places y x 3 y 6x 6 1 x 2 COFFR The area calculated to three decimal places is square units
Calculus
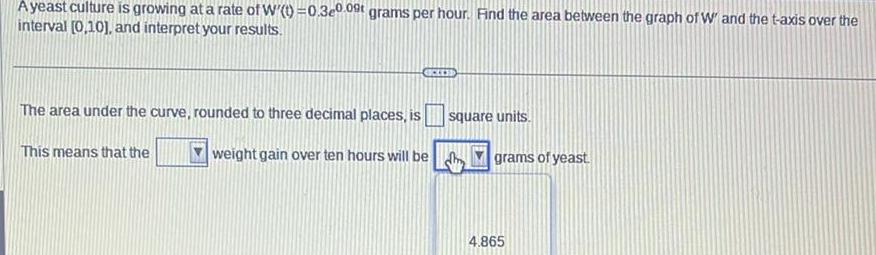
Definite IntegralsA yeast culture is growing at a rate of W t 0 3e0 09 grams per hour Find the area between the graph of W and the t axis over the interval 0 10 and interpret your results The area under the curve rounded to three decimal places is weight gain over ten hours will be This means that the CEES square units grams of yeast 4 865
Calculus
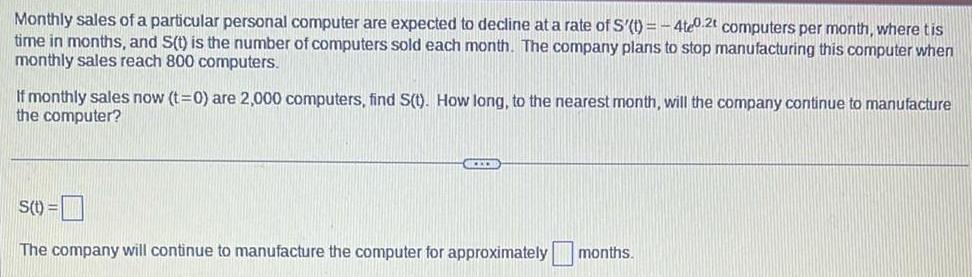
Definite IntegralsMonthly sales of a particular personal computer are expected to decline at a rate of S t 4te0 2t computers per month where tis time in months and S t is the number of computers sold each month The company plans to stop manufacturing this computer when monthly sales reach 800 computers If monthly sales now t 0 are 2 000 computers find S t How long to the nearest month will the company continue to manufacture the computer S t CECH The company will continue to manufacture the computer for approximately months
Calculus
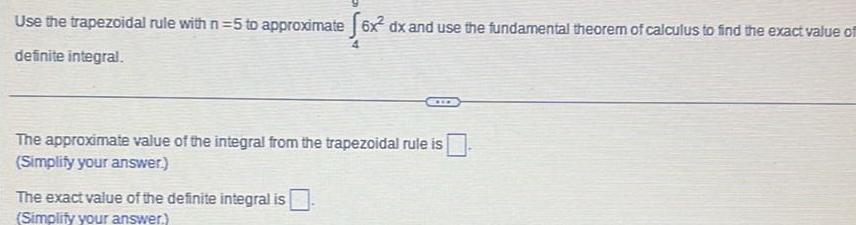
Application of derivativesUse the trapezoidal rule with n 5 to approximate 6x dx and use the fundamental theorem of calculus to find the exact value of definite integral The approximate value of the integral from the trapezoidal rule is Simplify your answer The exact value of the definite integral is Simplify your answer

Calculus
Definite IntegralsChoose the correct answer below OA P x k x dx OC Sk x dx C d OE SIP x K X k x dx OB S p x k x dx d OD k x p x dx OF Sp x dx y k x y p x cd
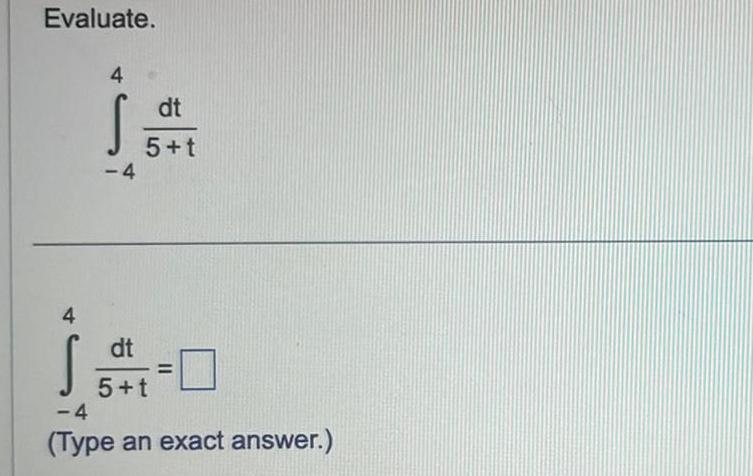
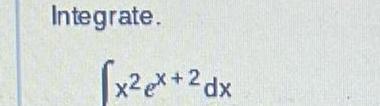
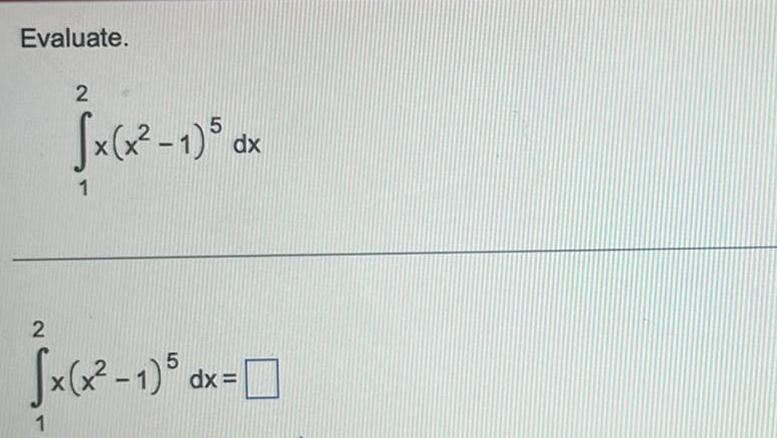
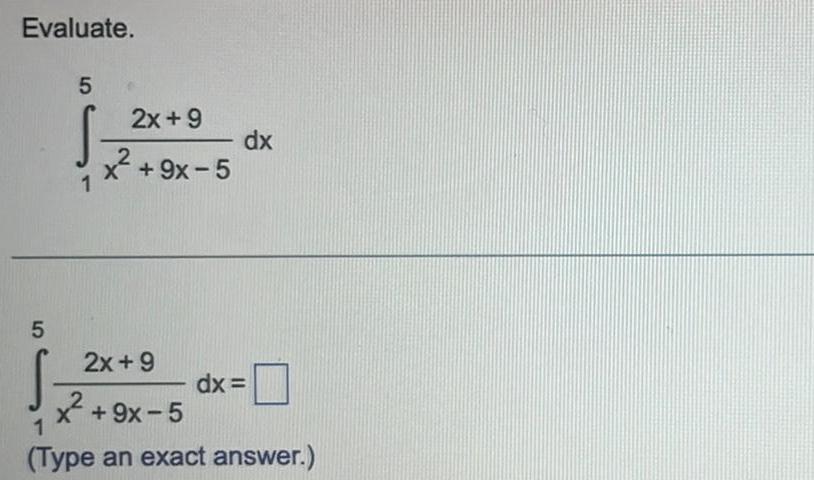

Calculus
DifferentiationEvaluate Be sure to check by differentiating Sex 20 dx S 6x 2 dx Type an exact answer Use parentheses to clearly denote the argument of each function


Calculus
Definite IntegralsUse the trapezoidal rule with n 3 to approximate 9 x4 dx T3 Round the final answer to two decimal places as needed Round all intermediate values to four decimal pl as needed

Calculus
Definite IntegralsThe concentration of particulate matter in parts per million t hours after a factory ceases operation for the day is given by the following formula C t Find the average concentration for the period from t 0 to t 4 C t 8In t 9 t 9 The average concentration of particulate matter for the time period from t 0 to t 4 is approximately million Do not round until the final answer Then round to four decimal places as needed parts per

Calculus
Definite IntegralsUse absolute value on a graphing calculator to find the area between the curve and the x axis over the given interval 13 y x ex 2 x 2 The area between the curve and the x axis over the given interval is Type an integer or decimal rounded to two decimal places as needed

Calculus
Indefinite Integration10The mouse is a particularly useful model for studying human disease because mice and humans are 100 genetically a identical all mice are in essence clones mice do not feel pain and discomfort d mice and humans are the only species whose genomes have been sequenced b C e approximately 90 of human disease associated genes are present in the mouse genome

Calculus
Limits & Continuity7 In the creation of a DNA profile a b C d minisatellites short tandem repeats introns exons are typically used

Calculus
Application of derivatives7 In the creation of a DNA profile a b C d minisatellites short tandem repeats introns exons are typically use
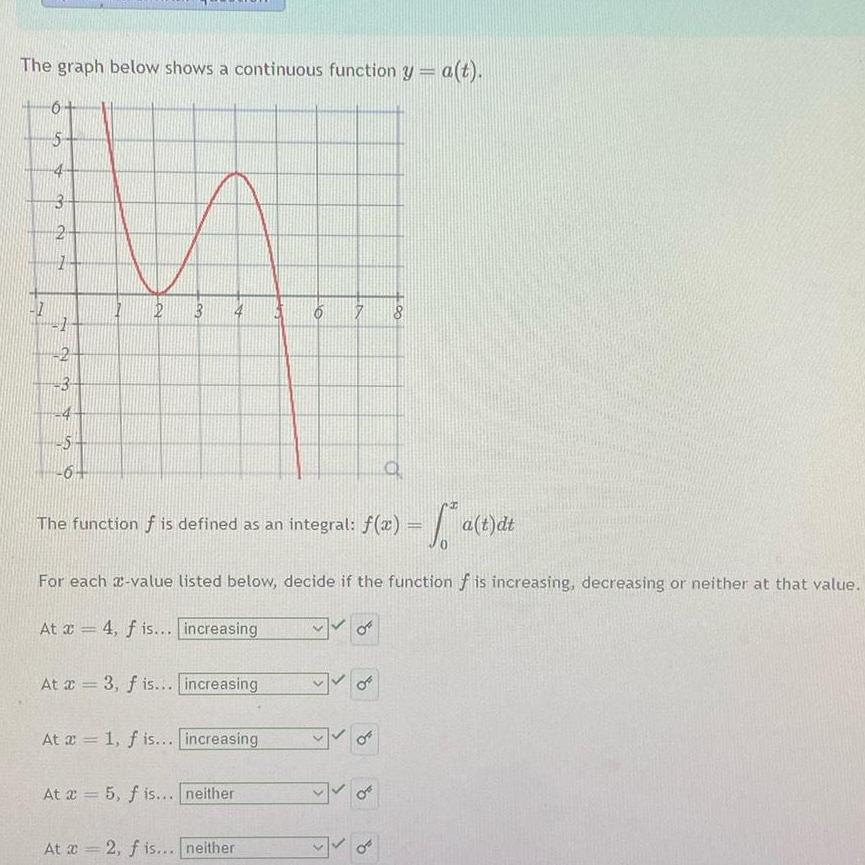
Calculus
Limits & ContinuityThe graph below shows a continuous function y a t F 6 5 A 3 2 2 2 2 3 5 6 2 3 A At 3 f is increasing The function is defined as an integral f x a t dt f At a 1 f is increasing 6 For each value listed below decide if the function f is increasing decreasing or neither at that value At 4 f is increasing At a 5 f is neither At 2 f is neither 7 8 OF OF a OF OF
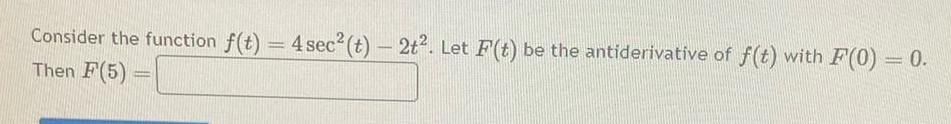
Calculus
Application of derivativesConsider the function f t 4 sec t 2t Let F t be the antiderivative of f t with F 0 0 Then F 5
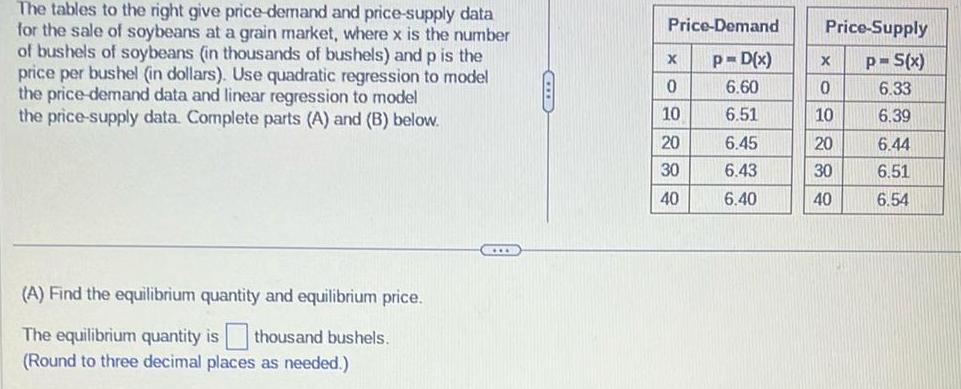
Calculus
Vector CalculusThe tables to the right give price demand and price supply data for the sale of soybeans at a grain market where x is the number of bushels of soybeans in thousands of bushels and p is the price per bushel in dollars Use quadratic regression to model the price demand data and linear regression to model the price supply data Complete parts A and B below A Find the equilibrium quantity and equilibrium price The equilibrium quantity is thousand bushels Round to three decimal places as needed GIIB Price Demand X 0 10 20 30 40 Price Supply p S x 6 33 6 39 p D x X 6 60 0 6 51 10 6 45 20 6 43 30 6 40 40 6 44 6 51 6 54