Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
Calculus
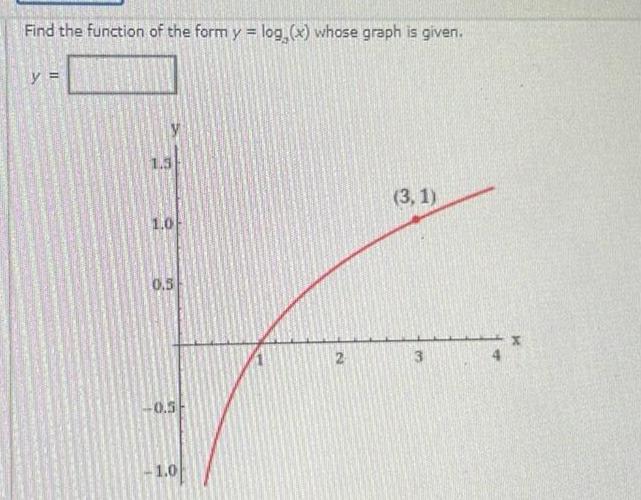
Application of derivativesFind the function of the form y log x whose graph is given y II 1 0 0 5 0 5 1 0 2 3 1 3
Calculus
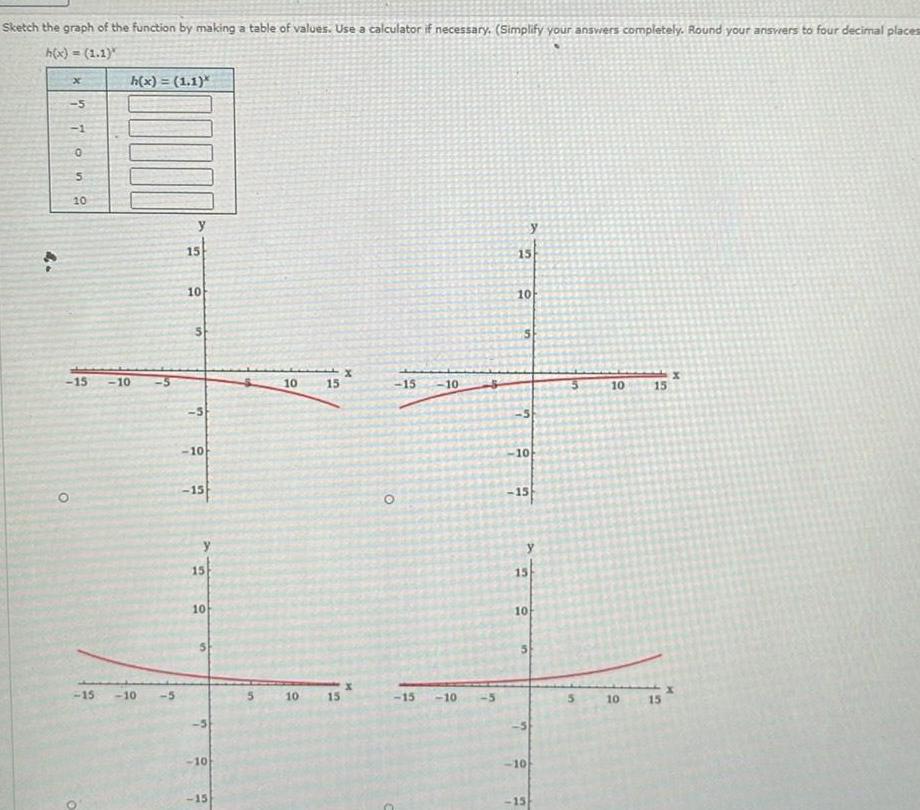
Vector CalculusSketch the graph of the function by making a table of values Use a calculator if necessary Simplify your answers completely Round your answers to four decimal places h x 1 1 x O 5 1 0 5 10 h x 1 1 15 10 15 10 5 y 15 10 5 S 10 15 y 15 10 5 10 15 10 10 15 15 X O 15 10 15 10 7 15 10 S 7 y 10 15 15 10 5 10 15 S 10 10 15 15 X
Calculus
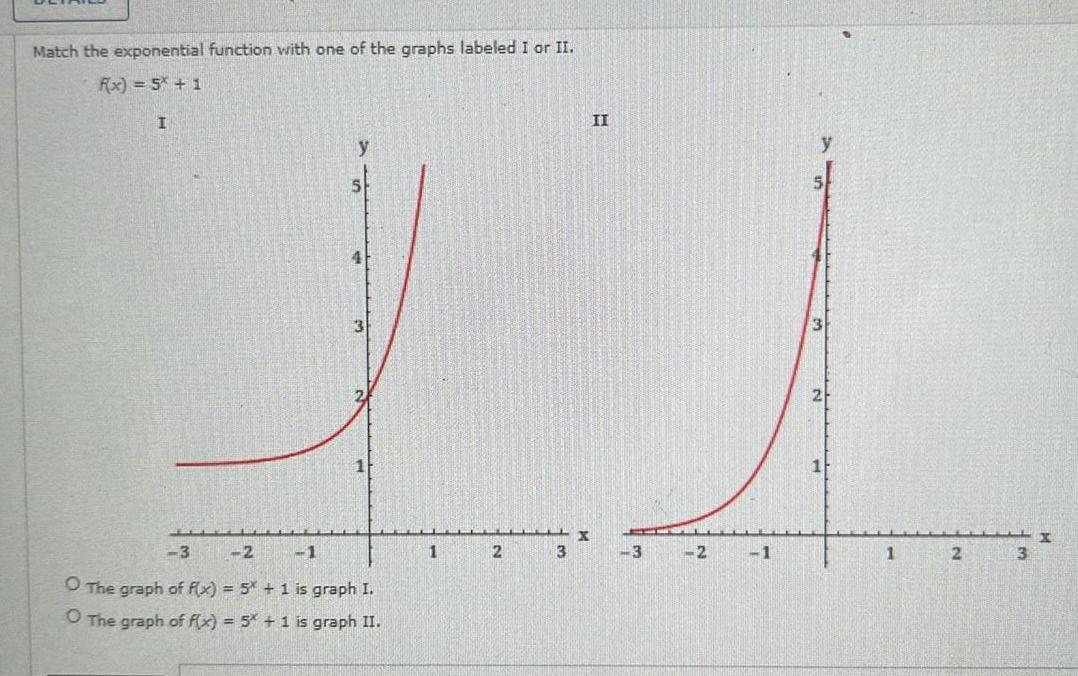
Vector CalculusMatch the exponential function with one of the graphs labeled I or II Rx 5x 1 I 5 3 3 2 1 O The graph of f x 5 1 is graph I O The graph of f x 5x 1 is graph II 1 2 3 X II 3 2 1 2 1 2 3 X
Calculus
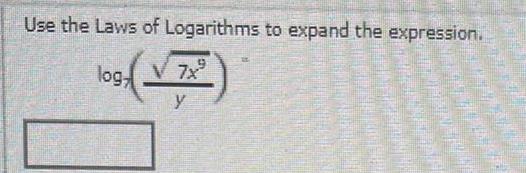
Application of derivativesUse the Laws of Logarithms to expand the expression log V 7x y HODINY FR

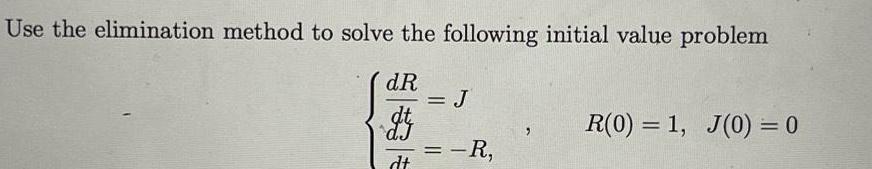
Calculus
Application of derivativesUse the elimination method to solve the following initial value problem dR dt dJ dt J R R 0 1 J 0 0
Calculus
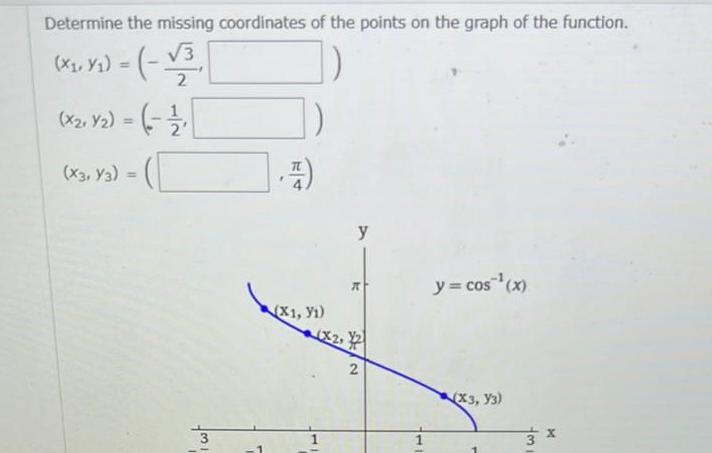
Vector CalculusDetermine the missing coordinates of the points on the graph of the function X X 3 x 2 X2 Y2 1 X3 Y3 ym 7 1 X1 y1 y R 22 7 45 y cos x X3 Y3 3 x

Calculus
Vector CalculusFill in the blank to complete the trigonometric identity Simplify your answer completely



Calculus
Limits & ContinuitySolve the logarithmic equation Round your answer to three decimal places log10 x 1 8

Calculus
Limits & ContinuityFind the inverse function of f informally Verify that f f x x and f f x x f x 5 x 4 f x
Calculus
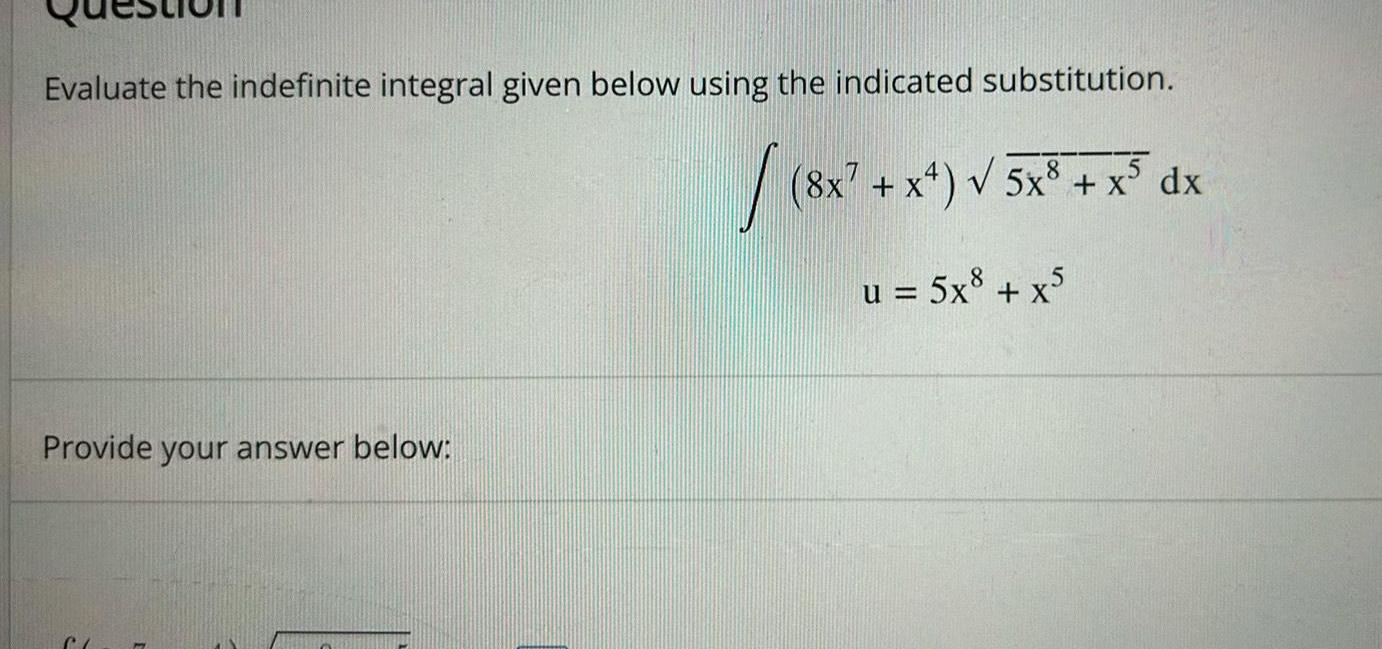
Indefinite IntegrationEvaluate the indefinite integral given below using the indicated substitution 8x x 5x x dx u 5x8 x5 Provide your answer below CL

Calculus
Application of derivativesA weight is oscillating on the end of a spring see figure The position of the weight relative to the point of equilibrium is given by y cos 8t 3 sin 8t where y is the displacement in meters and it is the time in seconds Find the times at which the weight is at the point of equilibrium y 0 for 0 sts 1 Round your answers to two decimal p Enter your answers as a comma separated list t H Equilibrium 4x4

Calculus
Vector CalculusFind all solutions of the equation in the interval 0 2m algebraically Use the table feature of a graphing utility to check your answers numerically 7 sec x 7 tan x 7
Calculus
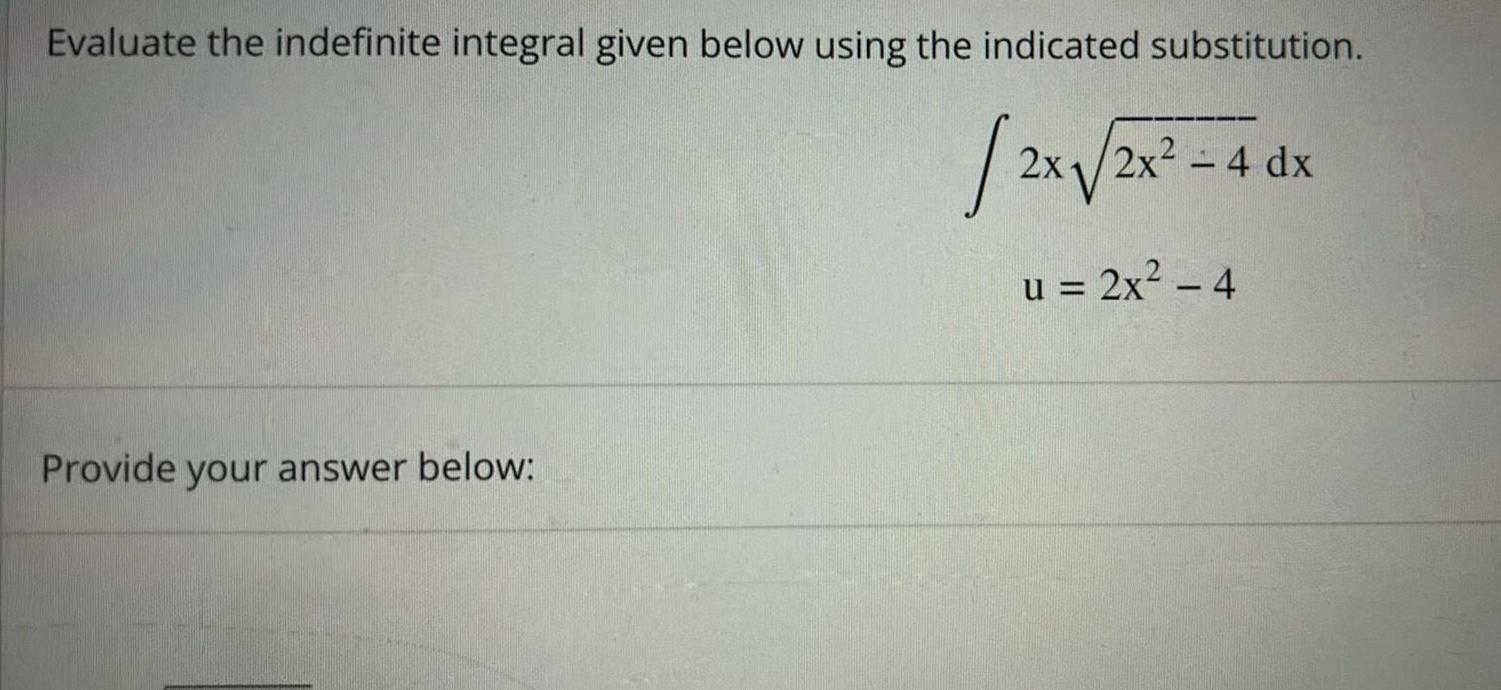
Indefinite IntegrationEvaluate the indefinite integral given below using the indicated substitution 2x 2x Provide your answer below 2x 4 dx u 2x 4

Calculus
Application of derivativesThe length of each of the two equal sides of an isosceles triangle is 10 meters see figure The angle between the two sides is 0 10 m a Write the area of the triangle as a function of 0 2 A 0 2 0 10 m b Write the area of the triangle as a function of and determine the value of 0 such that the area is a maximum A 0 radians

Calculus
Application of derivativesRewrite the expression in terms of the first power of the cosine Use a graphing utility to graph both expressions to verify that both forms are the same 3cos 2x

Calculus
Vector CalculusFactor the expression and use the fundamental identities to simplify Use a graphing utility to check your result graphically 2 sec x 2 sec x 2 sec x 2

Calculus
Application of derivativesUse the product to sum formulas to write the product as a sum or difference 2 sin 20 sin 50

Calculus
Application of derivativesUse inverse functions where necessary to solve the equation Use n as an integer constant Enter your answers as a comma separated list 2 cos x 13 sin x 8
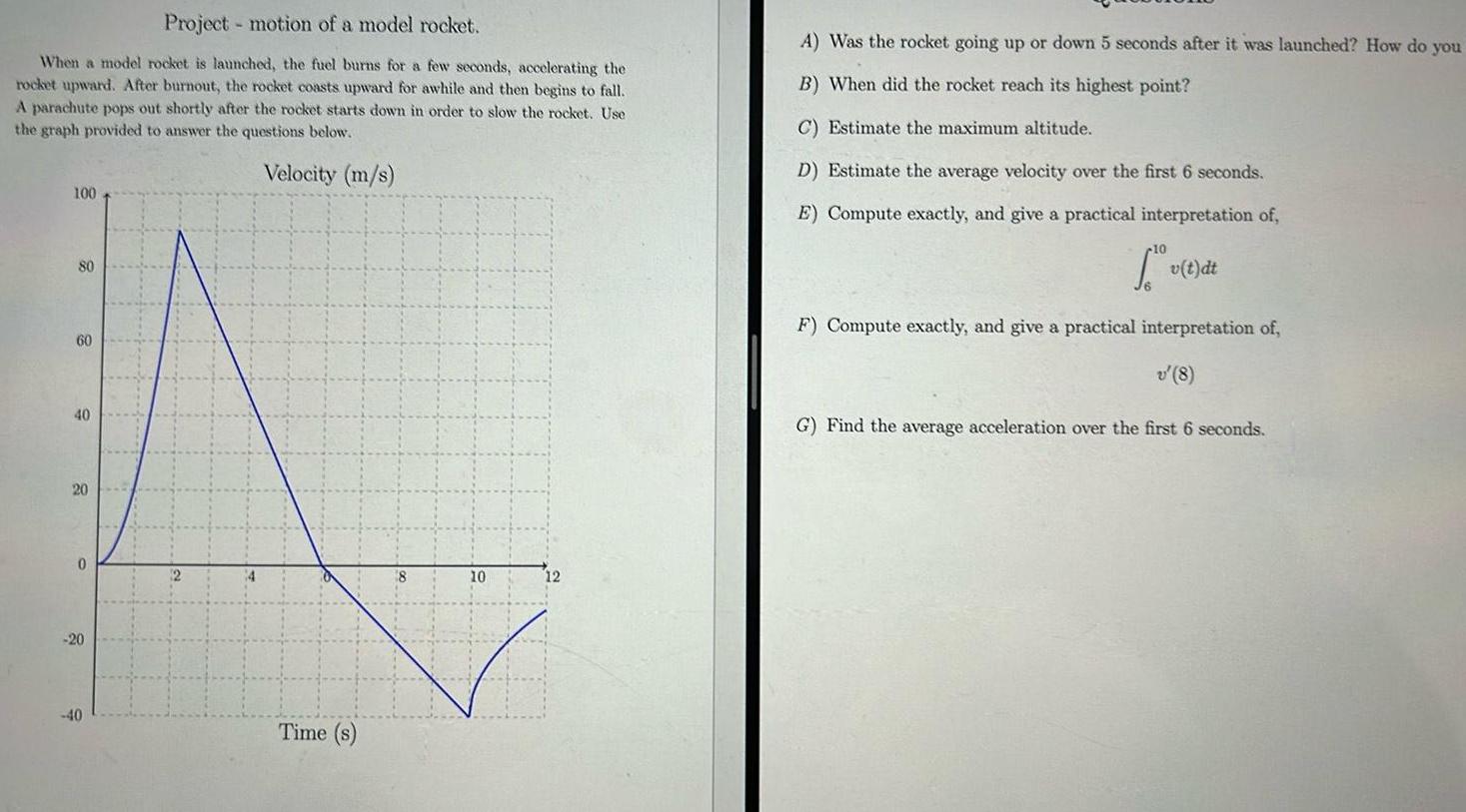
Calculus
Definite IntegralsProject motion of a model rocket When a model rocket is launched the fuel burns for a few seconds accelerating the rocket upward After burnout the rocket coasts upward for awhile and then begins to fall A parachute pops out shortly after the rocket starts down in order to slow the rocket Use the graph provided to answer the questions below Velocity m s 100 80 60 40 20 0 20 40 Time s 10 12 A Was the rocket going up or down 5 seconds after it was launched How do you B When did the rocket reach its highest point C Estimate the maximum altitude D Estimate the average velocity over the first 6 seconds E Compute exactly and give a practical interpretation of Tv t dt F Compute exactly and give a practical interpretation of v 8 G Find the average acceleration over the first 6 seconds

Calculus
Application of derivativesUse the properties of logarithms to verify the equation In 18 2 In 3 In 2 In 18 In 32 2 In 32 2 2 In 3 In 2 X In 3 X

Calculus
Application of derivativesThe relationship between the number of decibels and the intensity of a sound S in watts per square meter is given by 10910 10 12 B 10 log10 a Use the properties of logarithms to write the formula in a simpler form B b Use a graphing utility to complete the table Verify your answers algebraically 10 4 10 6 10 8 S n X DO so Po 100 10 10 n 10 12 an 10 14

Calculus
Application of derivativesUse the properties of logarithms to expand the expression as a sum difference and or constant multiple of logarithms Assume all variables are positive

Calculus
Application of derivativesRewrite the logarithm as a ratio of common logarithms and natural logarithms 9 lage 0 10 a common logarithms k 9 log 10 log a b natural logarithms


Calculus
Definite IntegralsWhich of the following statements is TRUE by the Comparison Test Hint When x e we have In x 1 We know 1 cos x 1 O fro e10 X foo dx e10 x2 ln x COS X X In x e10 X da converges because of a X 150 1 1 21 dx converges X COS X converges because ef 00 de diverges because dx converges because dx e 0 x2 1 00 1 e10 x2 de converges because S 1 X converges 1 x dx diverges dx diverges dx converges
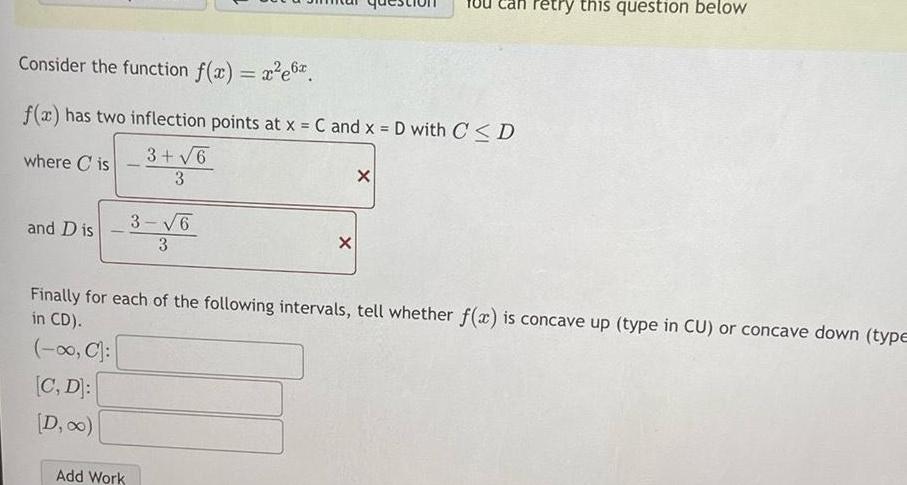
Calculus
Application of derivativesConsider the function f x x e6 f x has two inflection points at x C and x D with C D 3 6 where Cis 3 and Dis 3 6 3 Add Work X X retry this question below Finally for each of the following intervals tell whether f x is concave up type in CU or concave down type in CD C C D D

Calculus
Indefinite IntegrationThe questions in Level 1 are introductory problems The hints contain links to videos covering this content A Question 1 1 point Retake question Which of the following Type 1 Improper Integrals CONVERGE Select all that apply Ste 1 2 da dx 2 X Of 5 1 da of To 27 1 3 of a x dx da x sin x dx
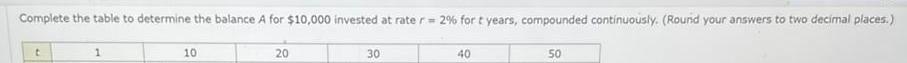
Calculus
Application of derivativesComplete the table to determine the balance A for 10 000 invested at rate r 2 for t years compounded continuously Round your answers to two decimal places 1 t 1 10 20 30 40 50

Calculus
Indefinite IntegrationUse a graphing utility to find the point of intersection if any of the graphs of the functions Round your result to three decimal places Enter NONE in any unused answer blanks x y y 110e0 01x y 13 500 x

Calculus
DifferentiationThe bounded area between the curves f x 15x4 and g x 15x is Your answer should be a number
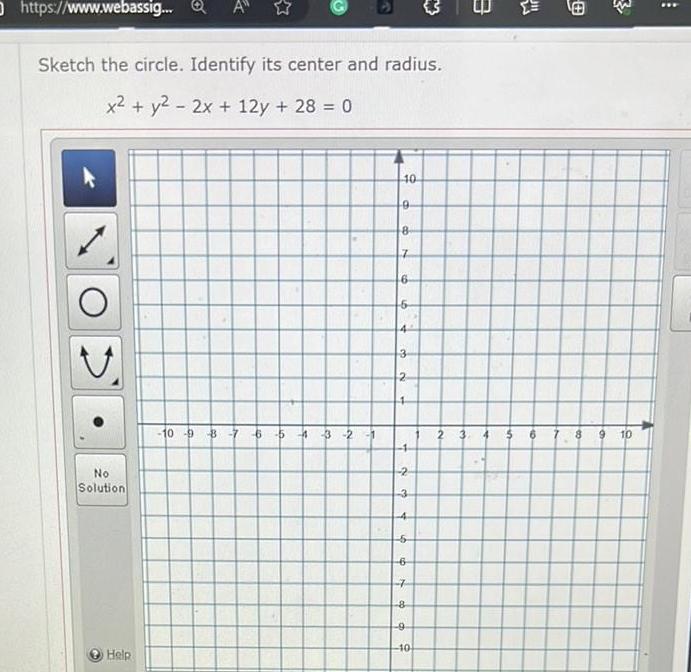
Calculus
Limits & Continuityhttps www webassig Q Sketch the circle Identify its center and radius x y 2x 12y 28 0 No Solution Help 10 9 8 7 6 5 3 2 1 40 9 8 7 6 6 4 3 2 4 4 2 3 4 5 6 7 8 9 10 56 8 9 10
Calculus
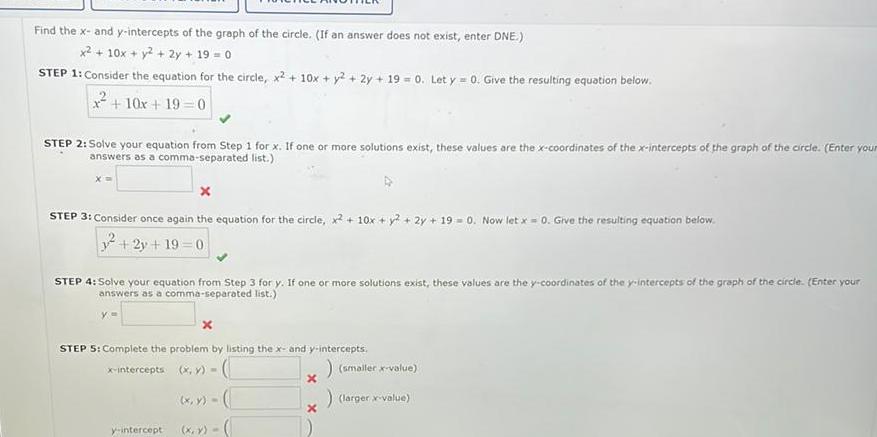
Application of derivativesFind the x and y intercepts of the graph of the circle If an answer does not exist enter DNE x 10x y 2y 19 0 STEP 1 Consider the equation for the circle x2 10x y2 2y 19 0 Let y 0 Give the resulting equation below 10x 19 0 STEP 2 Solve your equation from Step 1 for x If one or more solutions exist these values are the x coordinates of the x intercepts of the graph of the circle Enter your answers as a comma separated list x x STEP 3 Consider once again the equation for the circle x 10x y 2y 190 Now let x 0 Give the resulting equation below 2y 19 0 STEP 4 Solve your equation from Step 3 for y If one or more solutions exist these values are the y coordinates of the y intercepts of the graph of the circle Enter your answers as a comma separated list y x STEP 5 Complete the problem by listing the x and y intercepts x intercepts x y y intercept x y x y x x smaller x value larger x value
Calculus
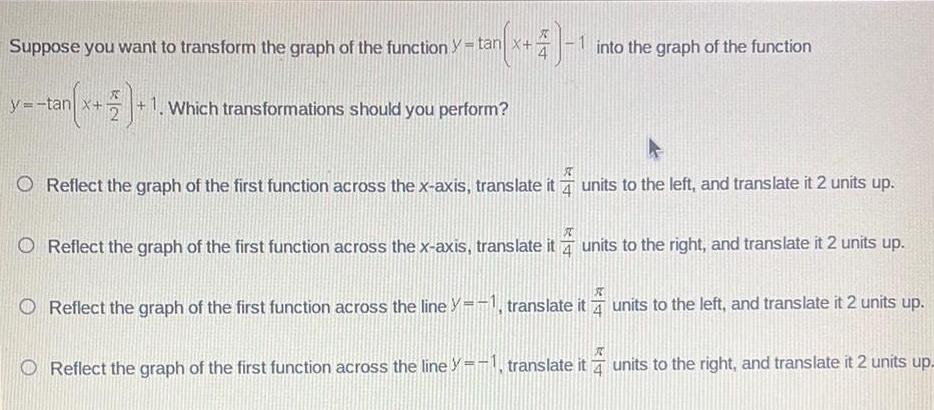
Definite Integralsy tan x 4 1 Suppose you want to transform the graph of the function t y tan tan x 1 1 Which transformations should you perform into the graph of the function X O Reflect the graph of the first function across the x axis translate it units to the left and translate it 2 units up ST Reflect the graph of the first function across the x axis translate it units to the right and translate it 2 units up 4 units to the left and translate it 2 units up Reflect the graph of the first function across the line y 1 translate it Reflect the graph of the first function across the line y 1 translate it units to the right and translate it 2 units up
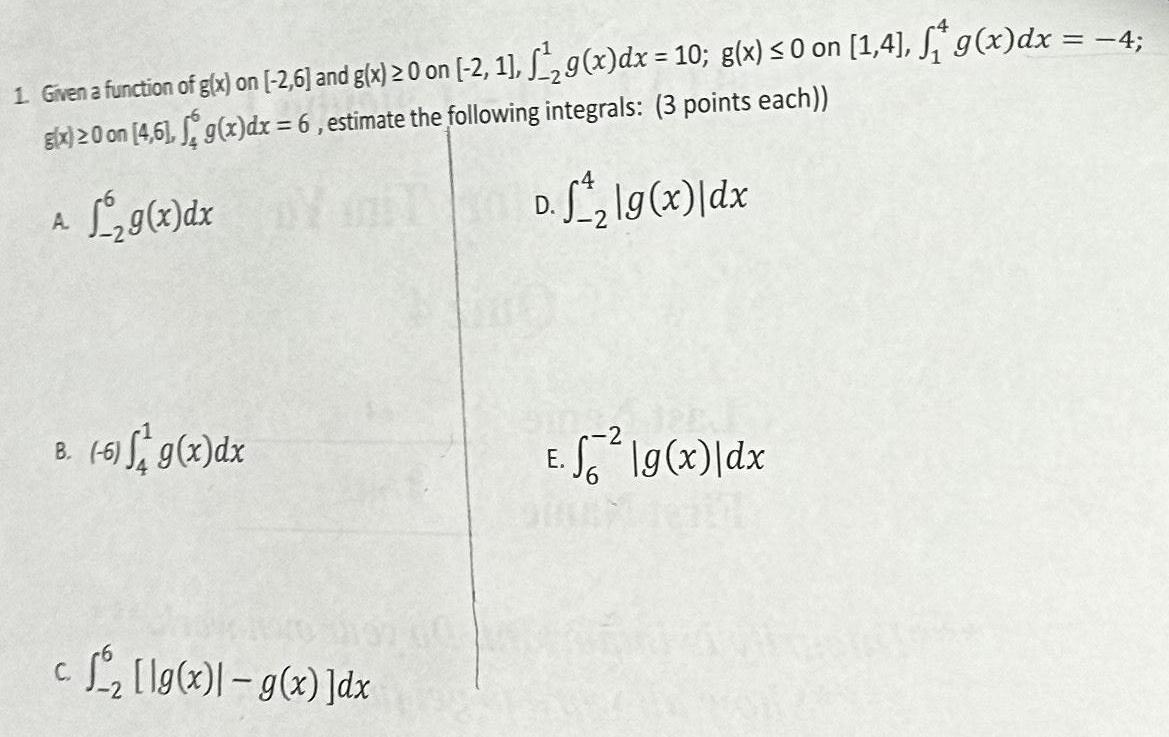
Calculus
Definite Integrals1 Given a function of g x on 2 6 and g x 0 on 2 1 g x dx 10 g x 0 on 1 4 g x dx 4 g x 0 on 4 6 g x dx 6 estimate the following integrals 3 points each D 2 lg x dx A L2g x dx B 6 g x dx c S g x g x dx E f lg x dx


Calculus
Definite IntegralsFigure 1 Rectangular garden fencing rdener has a large open space and wants to use fencing to create a rectangular garden with 2 er gardens of equal size as shown in Figure 4 He has 1000 feet of fencing Write an equation A w ibing the total area of the garden in terms of the width w

Calculus
Definite IntegralsThe marriage rate in a certain country is approximated by M t 8 3e 0 022t where M t is the number of marriages per 1000 people t years after 200 4 a Find the total number of marriages per 1000 people in the country from 2000 to 2004 Note that this is given by M t dt 0 b Find the total number of marriages per 1000 people in the country between 2004 and 2016
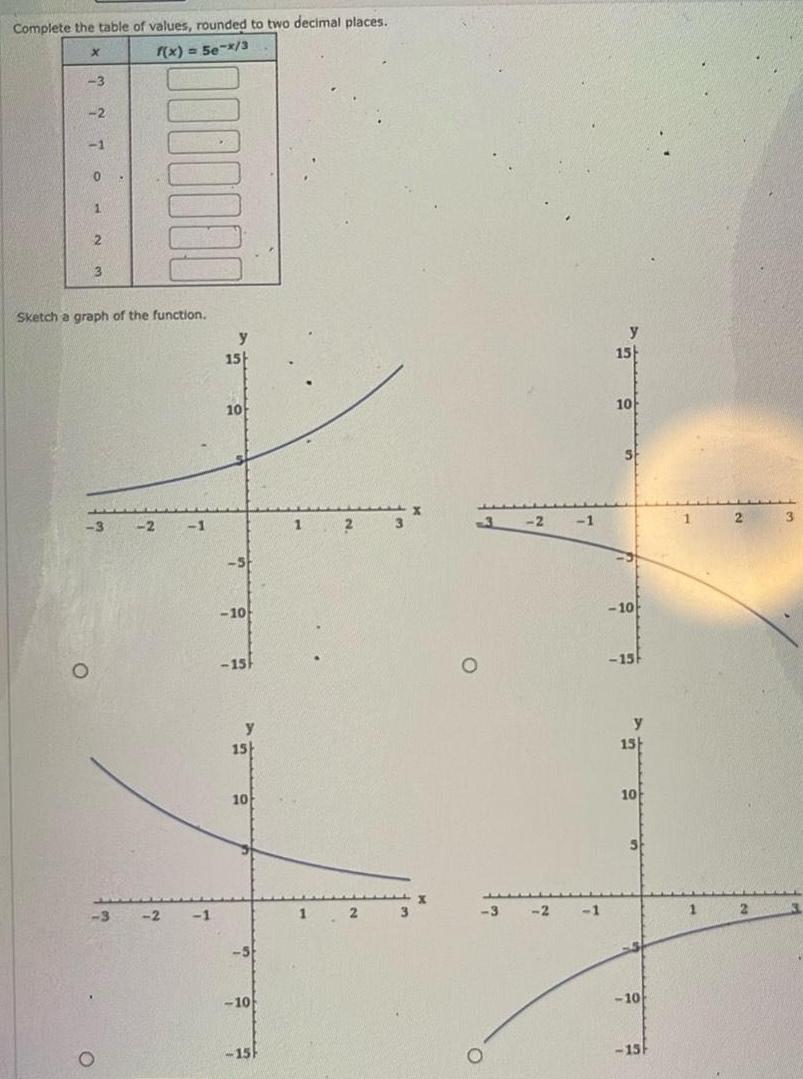
Calculus
Vector CalculusComplete the table of values rounded to two decimal places f x 5e x 3 X 3 2 1 0 1 2 3 Sketch a graph of the function 3 2 1 3 O 2 1 y 15 10 5 10 15 y 15 10 5 10 15 1 2 1 2 3 3 2 1 3 2 1 y 15 10 10 15 y 15 10 S 10 15 1 2 1 2
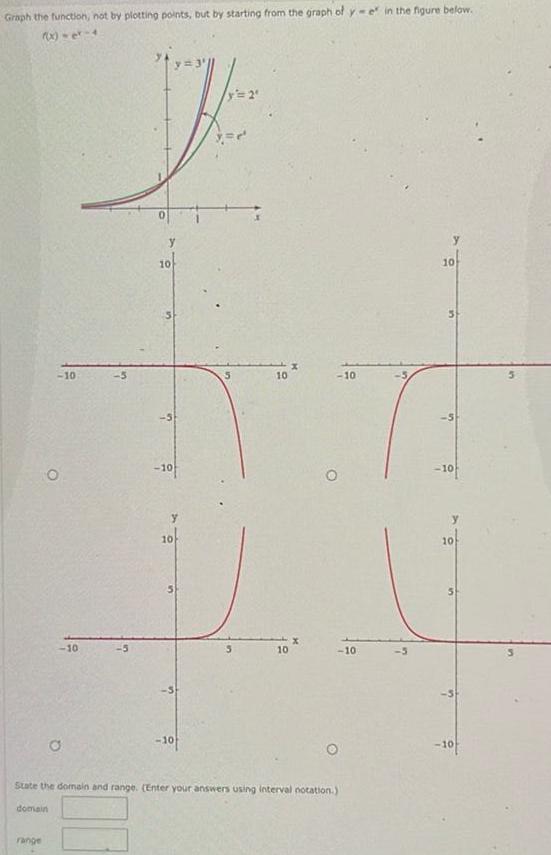
Calculus
Application of derivativesGraph the function not by plotting points but by starting from the graph of y e in the figure below 10 range O 10 O y 10 10 y 10 10 y 2 10 10 X 10 O 10 State the domain and range Enter your answers using interval notation domain y 10 10 10 10
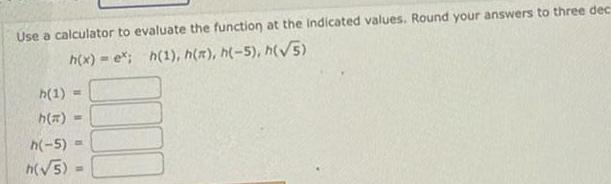
Calculus
Vector CalculusUse a calculator to evaluate the function at the indicated values Round your answers to three dec h x e h 1 h h 5 h 5 h 1 h h 5 h 5 W
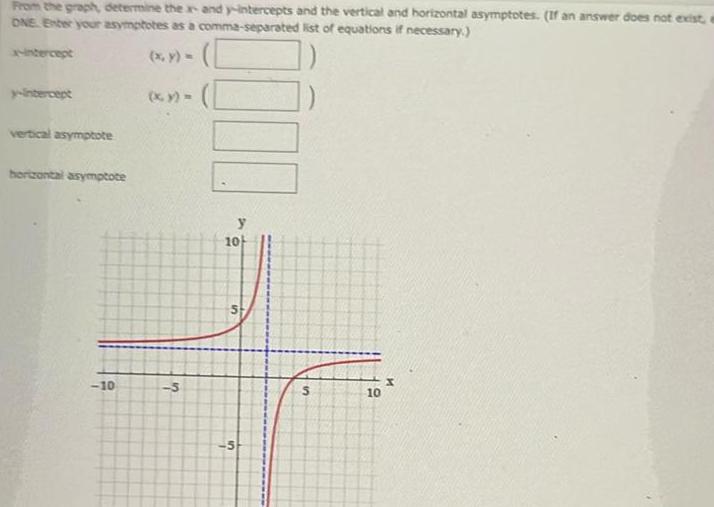
Calculus
Differential equationsFrom the graph determine the x and y intercepts and the vertical and horizontal asymptotes If an answer does not exist ONE Enter your asymptotes as a comma separated list of equations if necessary x intercept y intercept vertical asymptote horizontal asymptote 10 5 y 10 S 5 S 10 M

Calculus
Vector CalculusTue or False 12 x Let x x 1 2x 4 a The graph of r has a vertical asymptote x 1 O True O False b The graph of r has a vertical asymptote x 2 O True O False c The graph of r has a horizontal asymptote y 1 O True O False d The graph of r has a horizontal asymptote y O True O False

Calculus
Vector CalculusFind all horizontal and vertical asymptotes if any If an answer does not exist enter DNE Enter your answers as a comma separated list of equations r x 3 X 9 vertical asymptote s horizontal asymptote 10
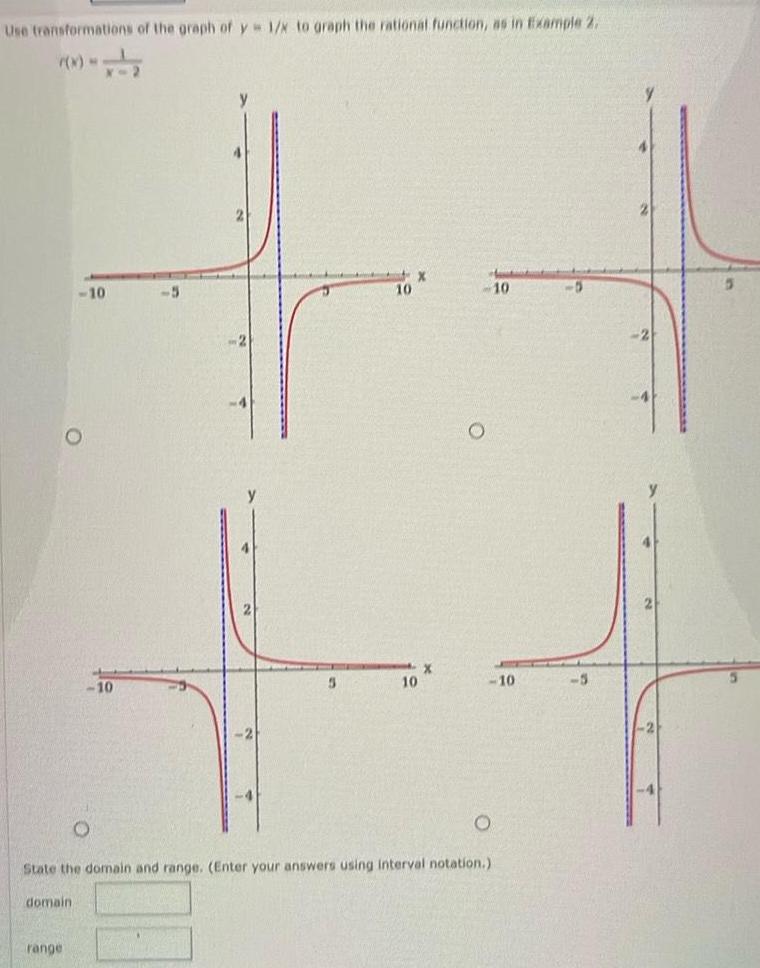
Calculus
Application of derivativesUse transformations of the graph of y 1 x to graph the rational function as in Example 2 domain 10 range 10 5 5 10 X 10 X 10 State the domain and range Enter your answers using interval notation 10 5 5 2

Calculus
Indefinite IntegrationQuestion 5 20 points 5 Find the moment of inertia in terms of its mass of a right circular cone of radius r and height h with respect to its axis h Axis