Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
Calculus
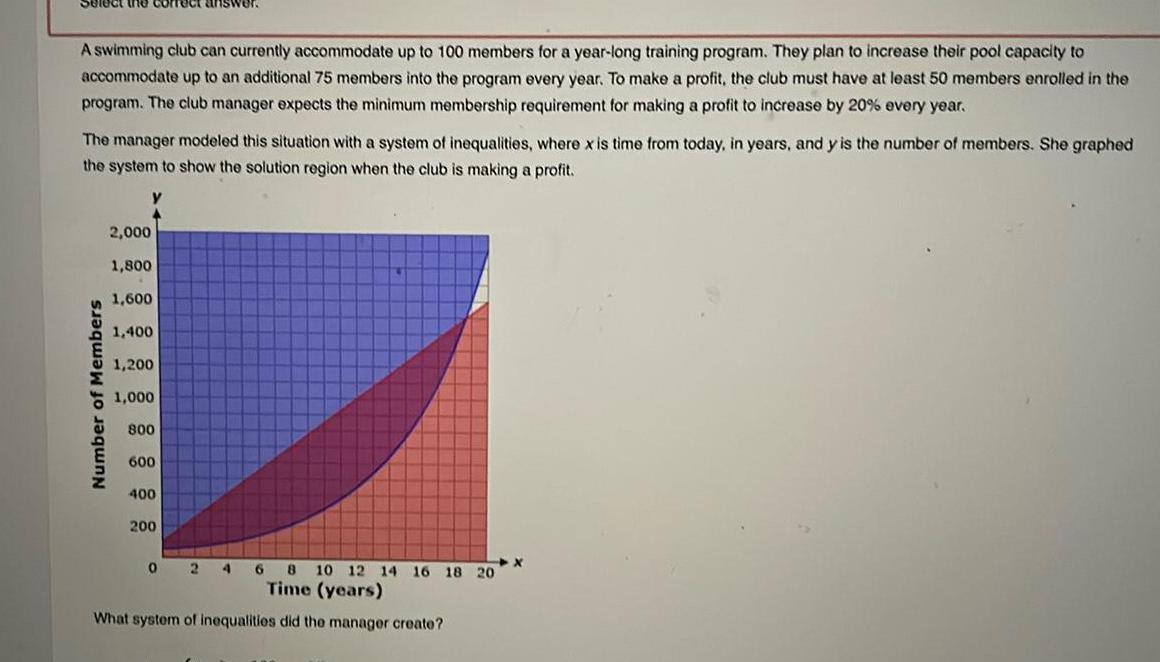
Limits & Continuitythe A swimming club can currently accommodate up to 100 members for a year long training program They plan to increase their pool capacity to accommodate up to an additional 75 members into the program every year To make a profit the club must have at least 50 members enrolled in the program The club manager expects the minimum membership requirement for making a profit to increase by 20 every year The manager modeled this situation with a system of inequalities where x is time from today in years and y is the number of members She graphed the system to show the solution region when the club is making a profit Number of Members 2 000 1 800 1 600 1 400 1 200 1 000 800 600 400 200 68 10 12 14 16 18 20 Time years What system of inequalities did the manager create 0 24

Calculus
Application of derivativesEstimate the area under the graph of f x over the interval 1 4 using ten approximating rectangles and right endpoints as sample points Rn Ln Repeat the approximation using left endpoints as sample points x 2 Repeat the approximation using midpoint as sample points M

Calculus
Definite IntegralsLet R be the region bounded by the following curves Use the shell method to find the volume of the solid generated when R is revolved about the y axis y 21 1 21x y 0 x 0 x 1 V Type an exact answer in terms of t GECED O Points 0 of 1 of 26 points 22 yu 21 1 21x
Calculus
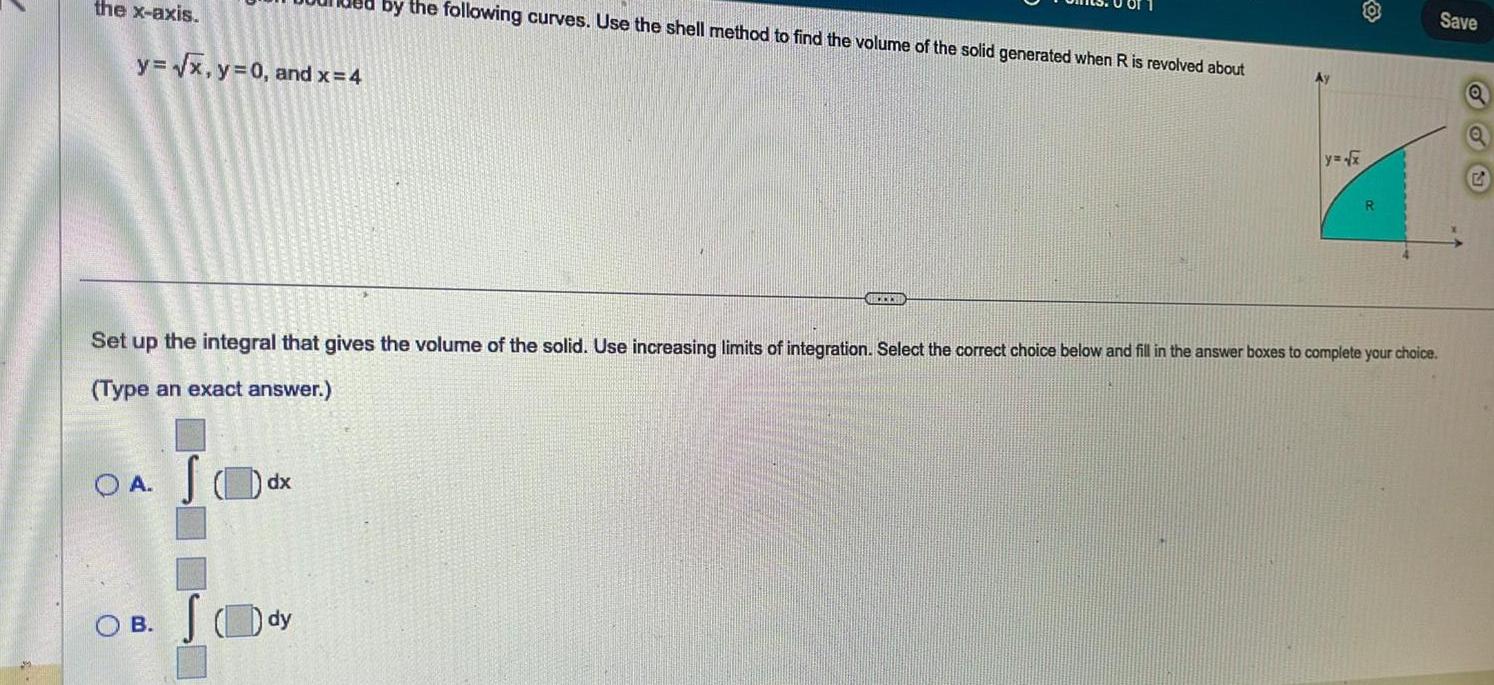
Definite Integralsthe x axis y x y 0 and x 4 OA dx OB JO by the following curves Use the shell method to find the volume of the solid generated when R is revolved about Set up the integral that gives the volume of the solid Use increasing limits of integration Select the correct choice below and fill in the answer boxes to complete your choice Type an exact answer dy BECCESSO y x R Save

Calculus
Vector CalculusPoints 0 of 1 Select the correct choices that complete the sentence below A region R is revolved about the y axis The volume of the resulting solid could in principle be found by using the disk washer method and integrating with respect to shell method and integrating with respect to Save or using
Calculus
Application of derivativesIdentify the integral Choose the correct answer below OA 2 f O C b 2n f x OD a b OB 2 g x f x dx a nethod that equals the volume of the resulting solid Tegloh bounded by the graphs of f and g and the lines x a and x b is revolved about the y axis Write the integra b 2x f x g x dx b a 2xx g x f x dx 2nx f x g x dx a
Calculus
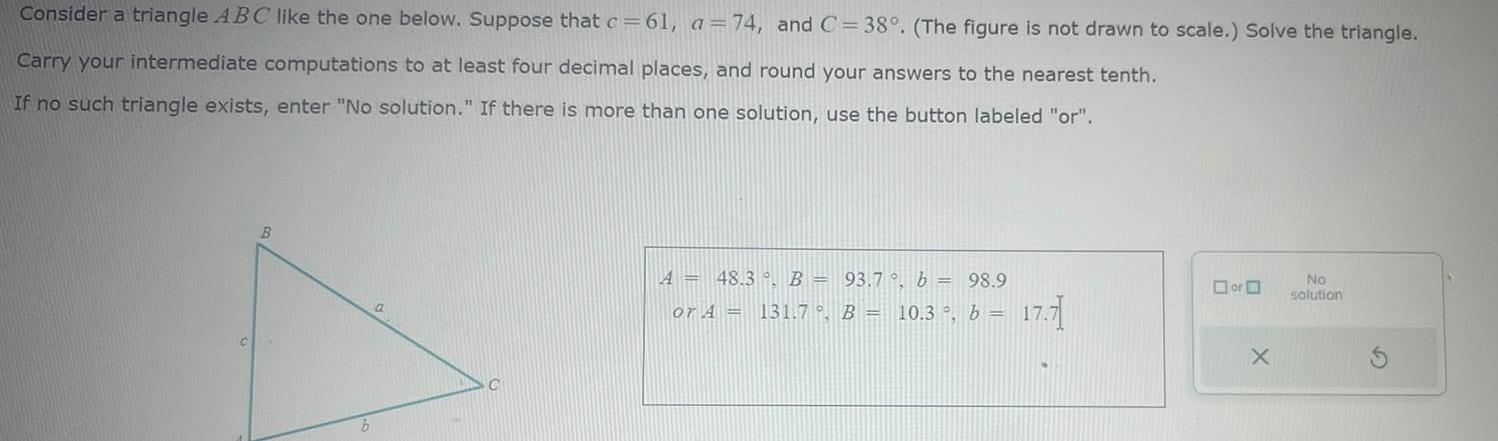
Vector CalculusConsider a triangle ABC like the one below Suppose that c 61 a 74 and C 38 The figure is not drawn to scale Solve the triangle Carry your intermediate computations to at least four decimal places and round your answers to the nearest tenth If no such triangle exists enter No solution If there is more than one solution use the button labeled or B b a A 48 3 B 93 7 b 98 9 or A 131 7 B 10 3 b 17 71 or X No solution

Calculus
DifferentiationA company determined that the marginal cost C x of producing the xth unit of a product is given by C x x 2x Find the total cost function C assuming that C x is in dollars and that fixed costs are 8000 C x

Calculus
Vector CalculusRemember that rectangular form is z a bi and that polar form is z r cos0 i sin 0 Take following number in polar form and convert it to rectangular form 10 cos 84 i sin 84 Round to the nearest hundredth The angle above provided is in degrees 2


Calculus
DifferentiationAn oil tanker aground on a reef is forming a circular oil slick about 0 2 foot thick To in cubic feet per minute at which the oil is leaking from dV estimate the rate dt the tanker it was found that the radius of the slick was increasing at 0 42 foot per dR dV minute 0 42 when the radius R was 400 feet Find dt C dt Y using 3 14 dV ft min dt Type an integer or a decimal Round to the nearest whole number as needed 2 A xR V 0 2A Tanker R

Calculus
Application of derivativesThe price p in dollars and demand x for wireless headphones are related by x 8 000 0 15p The current price of 95 is decreasing at a rate 5 per week Find the associated revenue function R p and the rate of change in dollars per week of revenue R p

Calculus
Application of derivativesA manufacturer of handcrafted wine racks has determined that the cost to produce x units per month is given by C 0 4x 9 000 How fast is the cost per month changing when production is changing at the rate of 15 units pe month and the production level is 80 units Costs are at the rate of Round to the nearest dollar as needed per month at this production level

Calculus
Application of derivativesA retail store estimates that weekly sales s and weekly advertising costs x both in dollars are related by 40 000 20 000 0 00025x The current weekly advertising costs are 4 000 and these costs are increasing at a rate of 600 per week Find the current rate of change of sales The current rate of change of sales is Round to the nearest dollar as needed per week

Calculus
Application of derivativesA 13 foot ladder is placed against a vertical wall Suppose the bottom of the ladder slides away from the wall at a constant rate of 2 feet per second How fast is the top of the ladder sliding down the wall when the bottom is 12 fee from the wall The ladder is sliding down the wall at a rate of Type an integer or a simplified fraction RYYB ft sec

Calculus
Differential equationsThe radius of a spherical balloon is increasing at the rate of 0 7 cm minute How fast is the volume changing when the radius is 7 4 cm The volume is changing at a rate of n minute cm Type an integer or a decimal Round to one decimal place as needed

Calculus
Application of derivativesA boat is being pulled toward a dock as shown in the figure to the right If the rope is being pulled in at the rate of 4 feet per second how fast is the distance between the dock and the boat decreasing when it is 3 feet from the dock The distance between the dock and the boat is decreasing by dock Round to the nearest thousandth as needed Boat Rope 4 ft Dock feet per second when the boat is 3 feet from the

Calculus
DifferentiationA box with an open top has a square base and four sides of equal height The volume of the box is 200 ft The height is 3 ft greater than both the length and the width If the surface area is 185 ft2 what are the dimensions of the box The width and length of the box is ft CHE x X
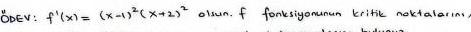
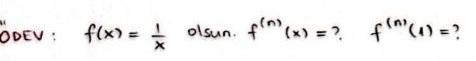


Calculus
DifferentiationA concert promoter sells tickets and has a marginal profit function given below where P x is in dollars per ticket Thi means that the rate of change of total profit with respect to the number of tickets sold x is P x Find the total profit from the sale of the first 170 tickets disregarding any fixed costs P x 4x 1152 The total profit is coded Y

Calculus
Application of derivativesA note card company has found that the marginal cost per card of producing x note cards is given by the function below where C x is the marginal cost in cents per card Find the total cost of producing 780 cards disregarding any fixed costs C x 0 05x 90 for x 1000 The total cost is cents
Calculus
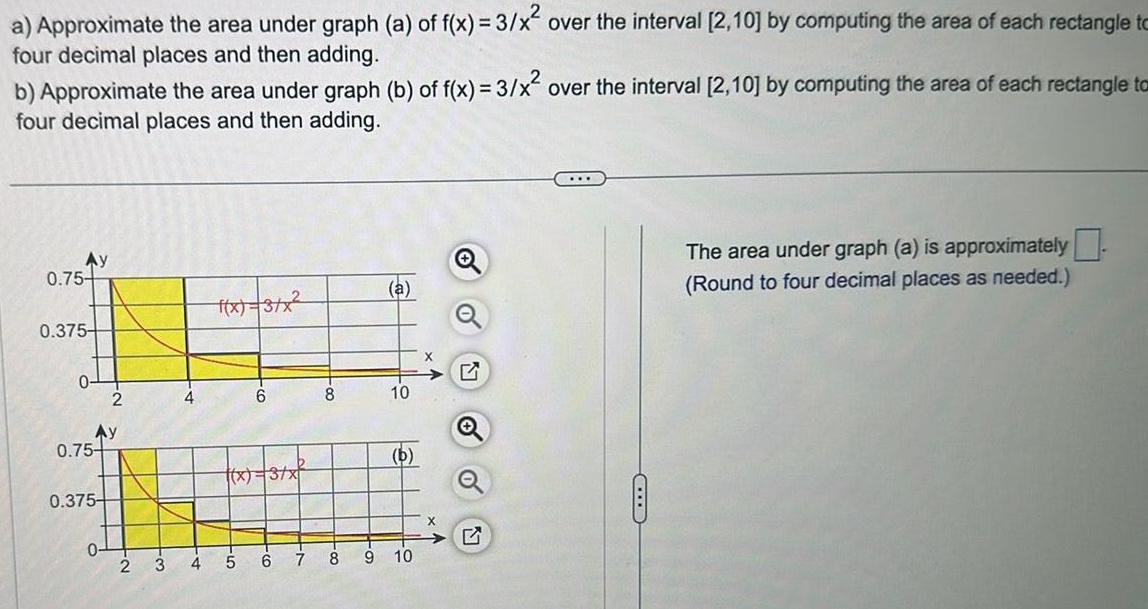
Limits & Continuitya Approximate the area under graph a of f x 3 x over the interval 2 10 by computing the area of each rectangle to four decimal places and then adding b Approximate the area under graph b of f x 3 x over the interval 2 10 by computing the area of each rectangle to four decimal places and then adding Ay 0 75 0 375 C 0 Ay 0 75 0 375 2 0 4 4 f x 3 x CO 5 6 x 3 x 6 00 8 a 10 b 7 8 9 10 X O o The area under graph a is approximately Round to four decimal places as needed
Calculus
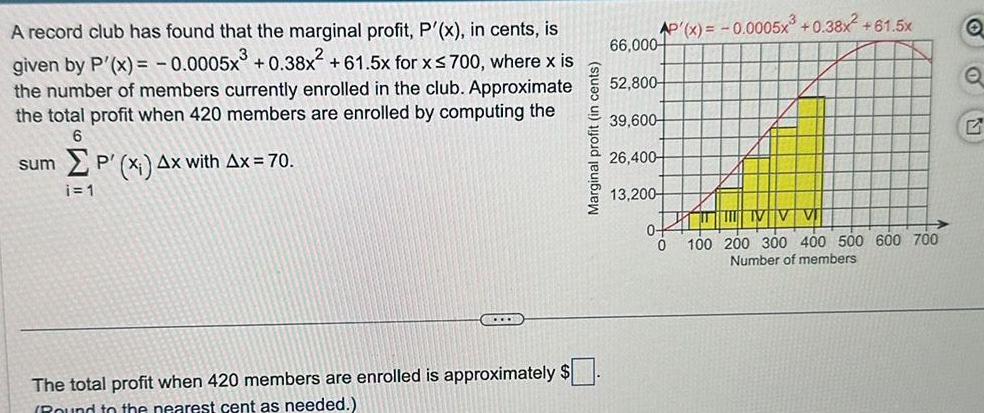
Definite IntegralsA record club has found that the marginal profit P x in cents is given by P x 0 0005x 0 38x 61 5x for x 700 where x is the number of members currently enrolled in the club Approximate the total profit when 420 members are enrolled by computing the 6 sum P x Ax with Ax 70 i 1 CO The total profit when 420 members are enrolled is approximately Round to the nearest cent as needed Marginal profit in cents AP x 0 0005x 0 38x 61 5x 66 000 52 800 39 600 26 400 13 200 0 0 VV 100 200 300 400 500 600 700 Number of members Q Q

Calculus
Application of derivativesSuppose that for a company manufacturing calculators the cost revenue and profit equations are given by C 90 000 30x R 300x 20 where the production output in 1 week is x calculators If production is increasing at a rate of 600 calculators per week when production output is 5 000 calculators Find the rate of increase decrease in cost revenue and profit A Costs are Simplify your answer P R C at the rate of S per week at this production level

Calculus
Differentiation1 5 points For each statement circle TRUE if the statement is always true Otherwise circle FALSE You do not need to justify your answer a 1 point A point p is an inflection point if f p 0 or if f p is undefined True b 1 point For a differentiable function defined on a closed interval a b the global maxi mum is either at a local maximum or at an endpoint True e 1 point If a function is increasing it has to be concave up C 1 point If p is a point so that f p 0 and p 0 then p is a local minimum True False True False d 1 point If f x is a continuous function with f 1 0 and f 1 4 then based on the Mean Value Theorem f 0 2 True False False False

Calculus
Limits & ContinuityA plane is 144 mi north and 186 mi east of an airport Find x the angle the pilot should turn in order to fly directly to the airport Round your answer to the nearest tenth of a degree W N 144 Airport 186 X E 0 X
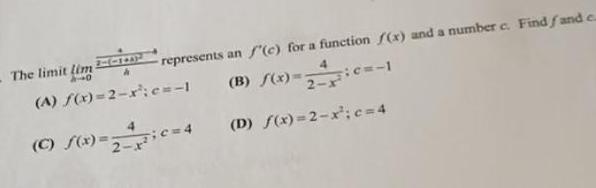
Calculus
Limits & ContinuityHAD A A f x 2 x c 1 B f x c 1 C S x 2 c 4 D f x 2 x c 4 represents an f c for a function f x and a number c Find fand e The limit lim 40
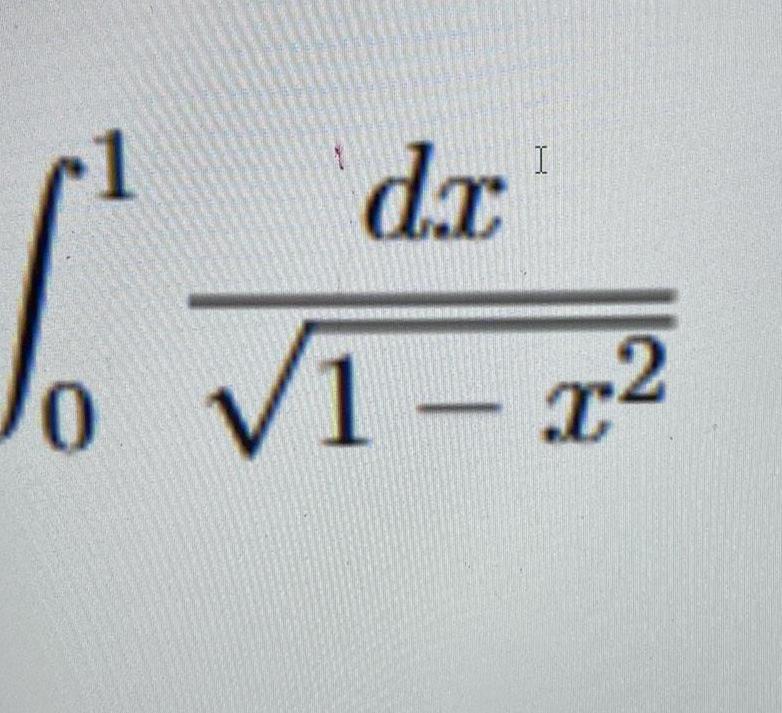
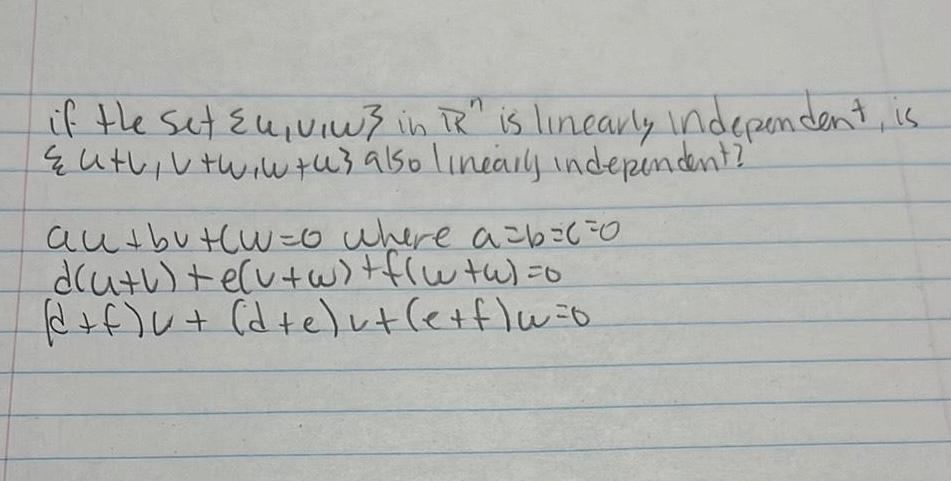
Calculus
Vector Calculusif the set Eu viw in TR is linearly independent is Euth vtwintus also linearly independent autbut w 0 where a 6 0 d u h e v w f w a 0 d f u d e vt e f w 0

Calculus
Limits & ContinuityWrite the first five terms of the arithmetic sequence Use the table feature of a graphing utility to verify your results as 15 814 91 5 a 32 03 34 as
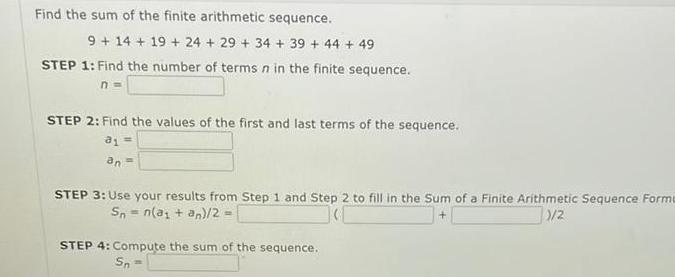
Calculus
Vector CalculusFind the sum of the finite arithmetic sequence 9 14 19 24 29 34 39 44 49 STEP 1 Find the number of terms n in the finite sequence n STEP 2 Find the values of the first and last terms of the sequence 81 an STEP 3 Use your results from Step 1 and Step 2 to fill in the Sum of a Finite Arithmetic Sequence Forme 1 2 Sn n a an 2 STEP 4 Compute the sum of the sequence Sn

Calculus
Vector CalculusA hardware store makes a profit of 25 000 during its first year The store owner sets a goal of increasing profits by 8000 each year for 5 years Assuming that this goal is met find the total profit during the first 6 years of business Need Help Read It


Calculus
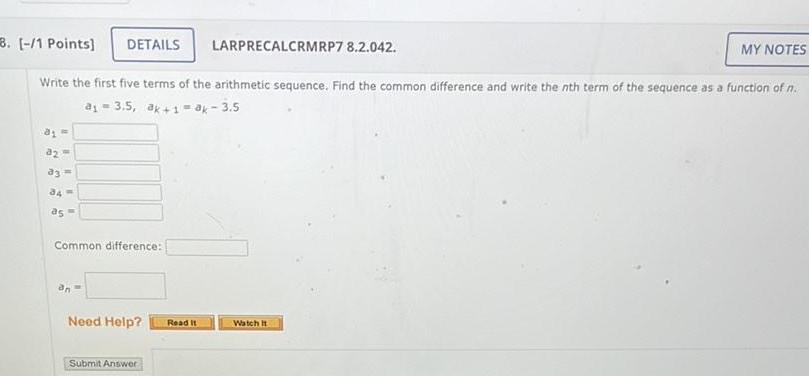
Limits & Continuity3 1 Points DETAILS LARPRECALCRMRP7 8 2 042 Write the first five terms of the arithmetic sequence Find the common difference and write the nth term of the sequence as a function of n a 3 5 ak 1 ak 3 5 12 93 34 as Common difference an Need Help Submit Answer Read It Watch t MY NOTES

Calculus
Vector CalculusThe first two terms of the arithmetic sequence are given Find the missing term Use the table feature of a graphing utility to verify your results a 6 3 19 ag

Calculus
DifferentiationWrite the first five terms of the arithmetic sequence Use the table feature of a graphing utility to verify your results a 9 d 1 12 a1 32 a3 34 35
Calculus
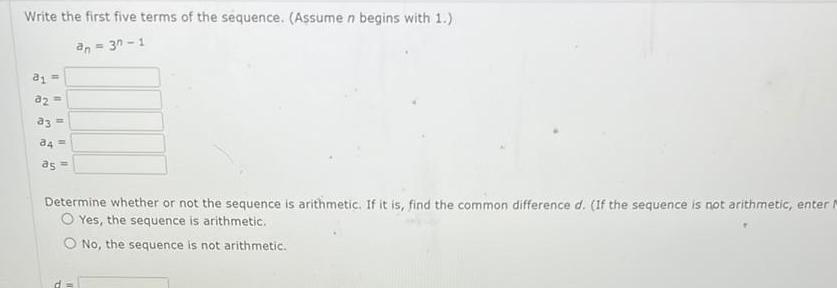
DifferentiationWrite the first five terms of the sequence Assume n begins with 1 an 3n 1 81 10 1 a3 34 as Determine whether or not the sequence is arithmetic If it is find the common difference d If the sequence is not arithmetic enter Yes the sequence is arithmetic O No the sequence is not arithmetic d

Calculus
DifferentiationDetermine whether the sequence is arithmetic If so find the common difference d If the sequence is not arithmetic enter NONE 6 10 14 18 22 O Yes the sequence is arithmetic O No the sequence is not arithmetic
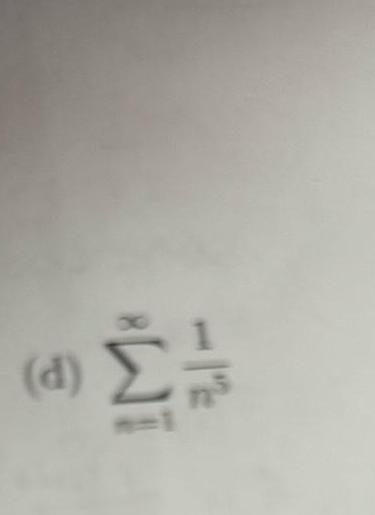
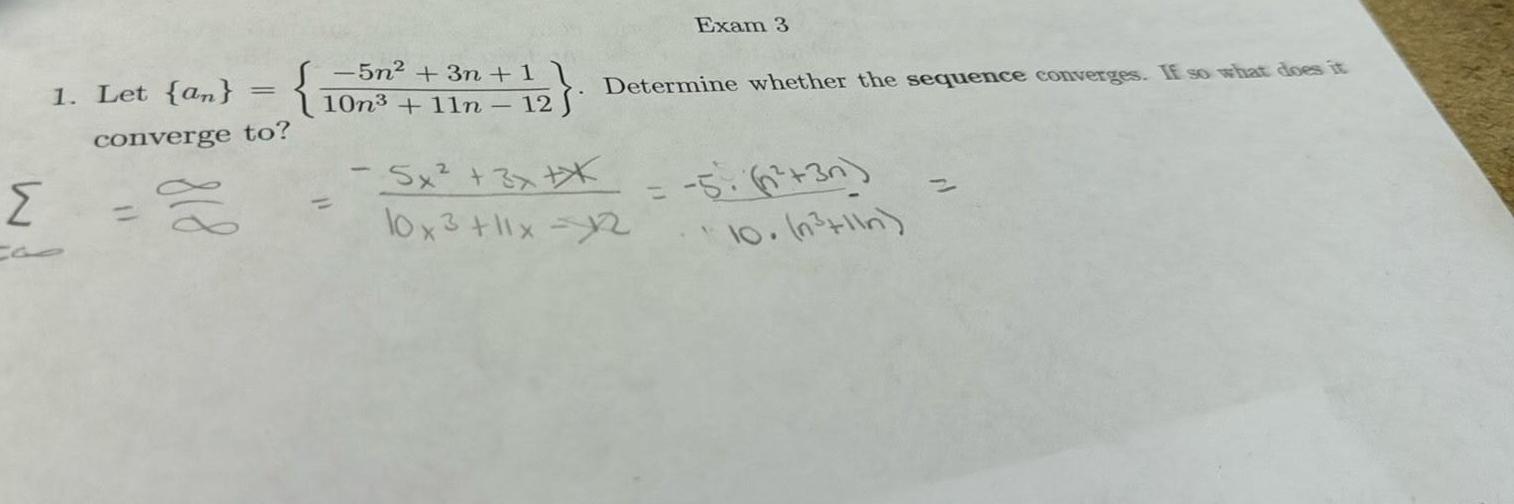
Calculus
Limits & Continuity1 Let an converge to D 5n 3n 1 10n 11n 12 5x 3x XX Exam 3 Determine whether the sequence converges If so what does it 10x3 11x 2 5 3n 10 n 1 n
Calculus
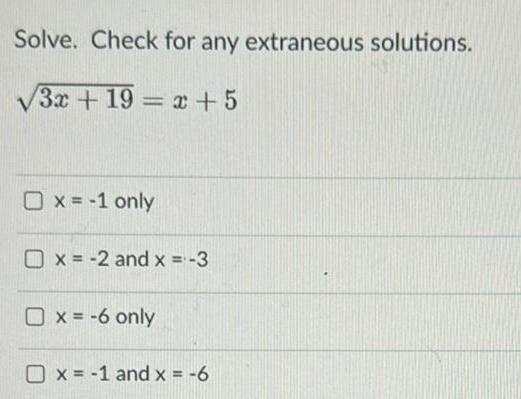
Application of derivativesSolve Check for any extraneous solutions 3x 19 x 5 O x 1 only x 2 and x 3 x 6 only x 1 and x 6
Calculus
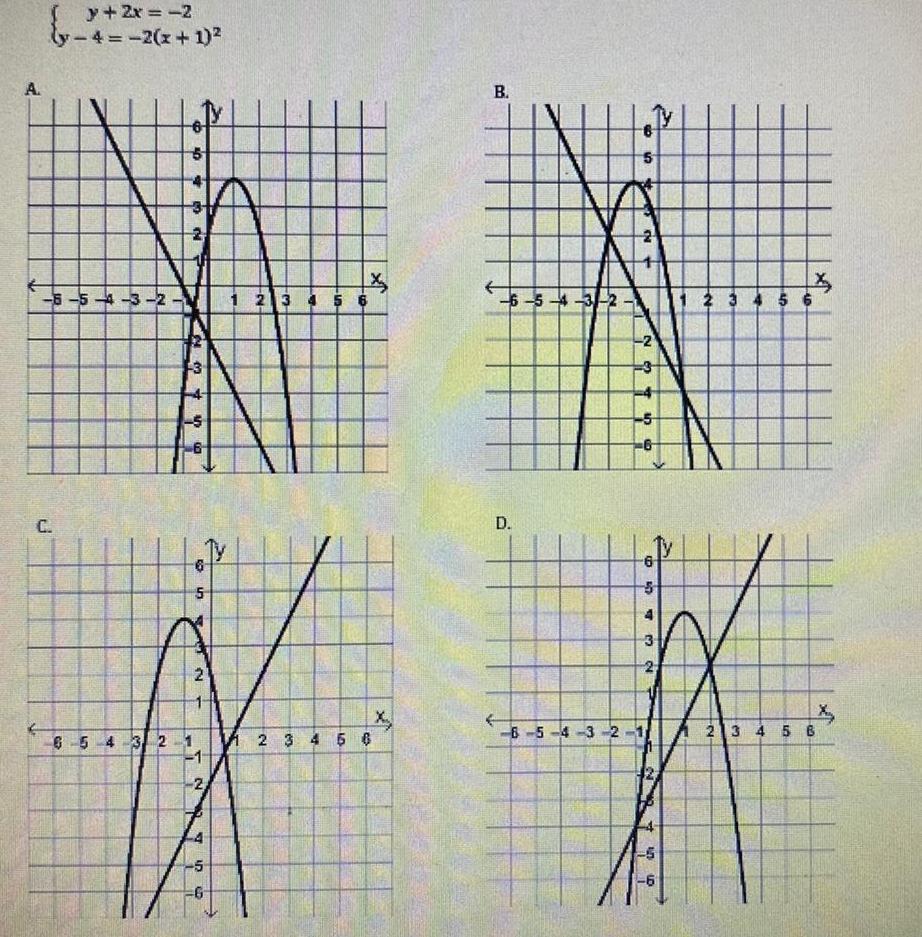
Differential equationsA y 2x 2 ly 4 2 x 1 6 5 4 3 2 C 2 3 4 5 6 B 5 A N 6 5 4 3 2 1 1 2 ST ch 6 x 1 2 3 4 5 6 1 2 3 4 5 6 x X B 6 5 4 3 2 D 5 2 2 19 5 6 6 57 4 6 5 4 3 2 1 12 10 1 2 3 4 5 6 AT LD X 2 3 4 5 6 X
Calculus
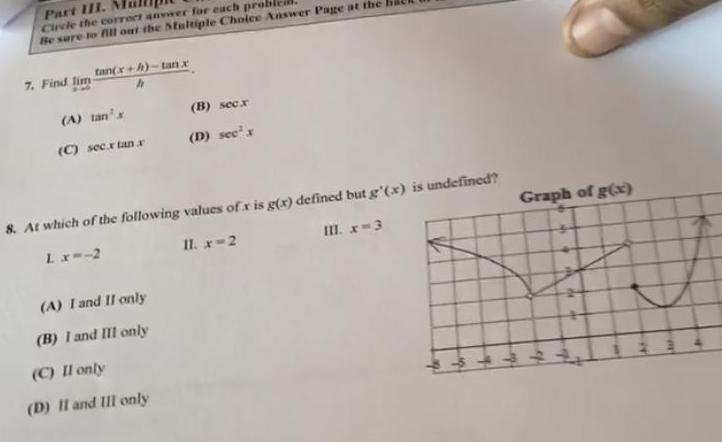
Application of derivativesPart III Circle the correct answer for each proble Be sure to fill out the Multiple Choice Answer Page at the tan x h tan x 7 Find lim A tan s C sec x tan x B sec x D see x 8 At which of the following values of x is g x defined but g x is undefined L x 2 II x 2 III x 3 A I and II only B I and III only C II only D II and III only Graph of g x

Calculus
Differentiation12 16 x 7 1 hint Ax is the same as h A 1 2m C 1 1 2r Inr C f x lim A 40 A f x lim 1 3cos o 7 2x which of the following will calculate the derivative of f x 2r Ar 2x x Ax 1x 1 Ar 0 2 0 3sin 0 what is f 0 f 0 1 3 cos 0 o 2 x 4r 2x x x 1 x 1 Ar B f 0 B 0 1 2ln D S 1 2m D f 0 2x Ar 2x B f x Ar 1 x 1 2 x 4x 2x D f x x 4x 1x 1 1 3 0 sin 0 o Ar 1 3 0 cos 0 Ar
Calculus
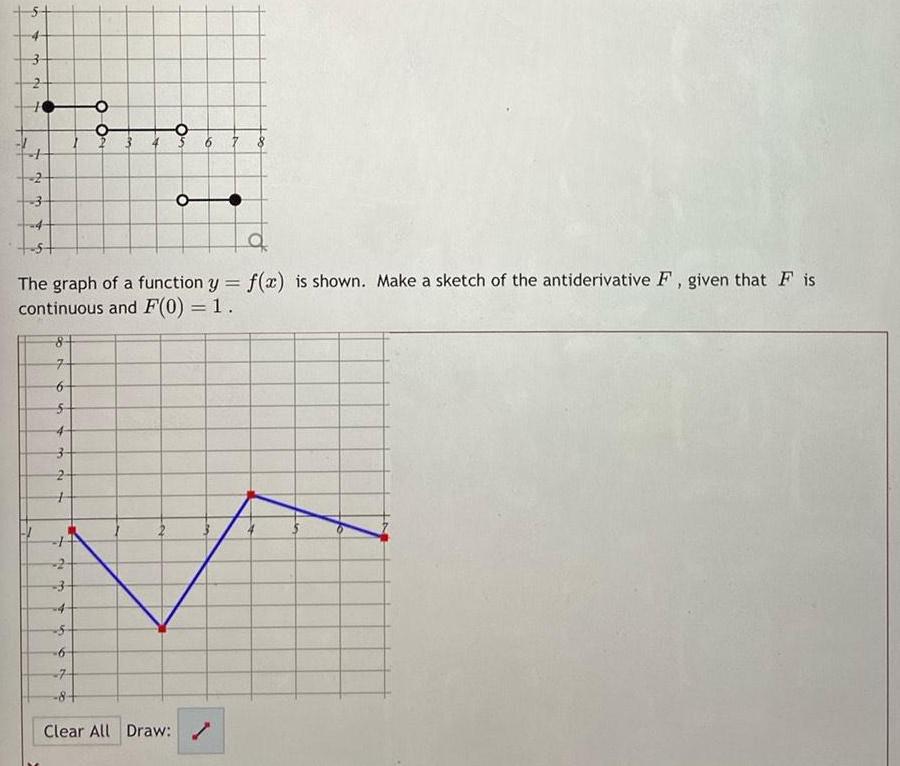
Application of derivatives5 3 O 2 34 a The graph of a function y f x is shown Make a sketch of the antiderivative F given that F is continuous and F 0 1 7 5 20 2 m 6 2 5 6 7 8 Clear All Draw

Calculus
Application of derivatives1 2 c If k x g x AM 2 1 2 9 x 5 2 sl a x 4 2 MIN find k 1 3 points 1 6 The functions f x and g x are differentiable for all values of x Selected values for Cry and g x and their derivatives are shown in the chart above a If s x f x g x find 2 1 point b If h x f x g x find 1 2 points 4 d If f x e f x find 1 Leave your answer in terms of e 2 points

Calculus
Application of derivativesalues are given in is permitted 17 Consider the function f x x x 11 a Find the average rate of change of f x on 0 6 2 points b Find the instantaneous rate of change of f x when x 4 2 points c Write an equation of the line tangent to fat the point where x 4 2 points Still using f x above if g x f x find all values of x where the tangent lines to g am Horizontal Show how you arrive at your answer 3 points