Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
Calculus
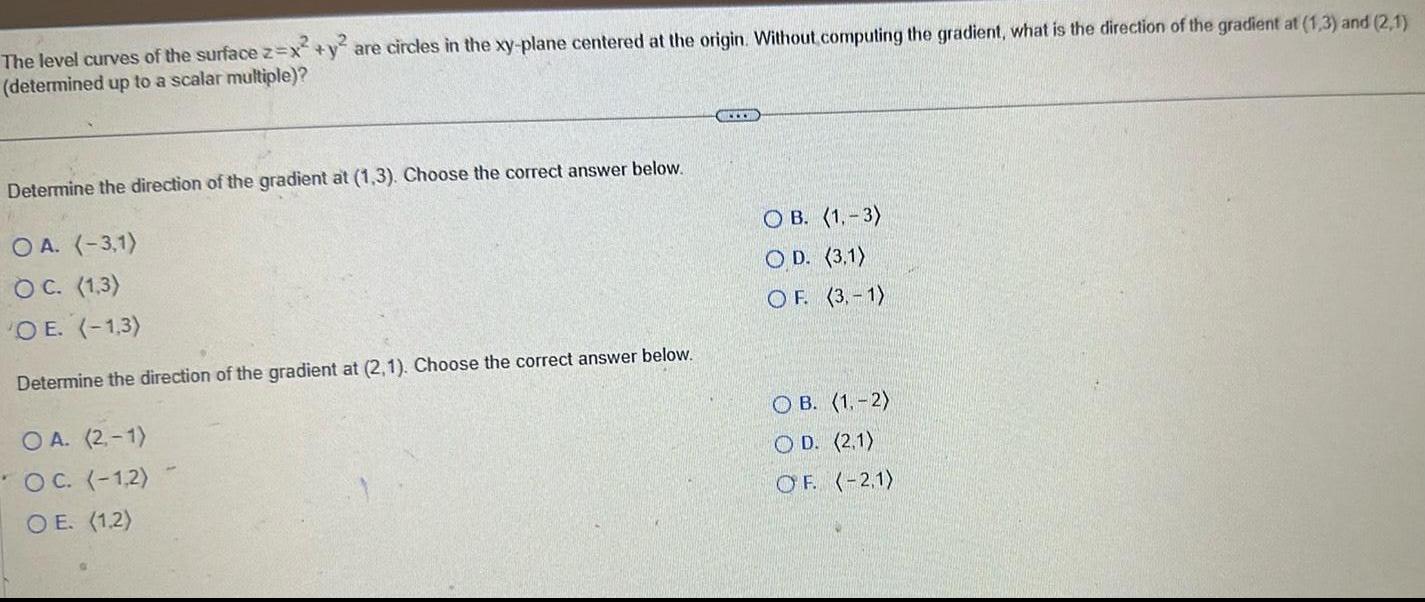
Vector CalculusThe level curves of the surface z x y are circles in the xy plane centered at the origin Without computing the gradient what is the direction of the gradient at 1 3 and 2 1 determined up to a scalar multiple Determine the direction of the gradient at 1 3 Choose the correct answer below OA 3 1 OC 1 3 O E 1 3 Determine the direction of the gradient at 2 1 Choose the correct answer below OA 2 1 OC 1 2 OE 1 2 CCC OB 1 3 OD 3 1 OF 3 1 OB 1 2 O D 2 1 OF 2 1

Calculus
DifferentiationCompute the directional derivative of the function g x y sin x x 3y at the point P 2 3 in the direction The directional derivative is Type an exact answer using as needed 14 3 5 5 Be sure to use a unit vector for the direction vector
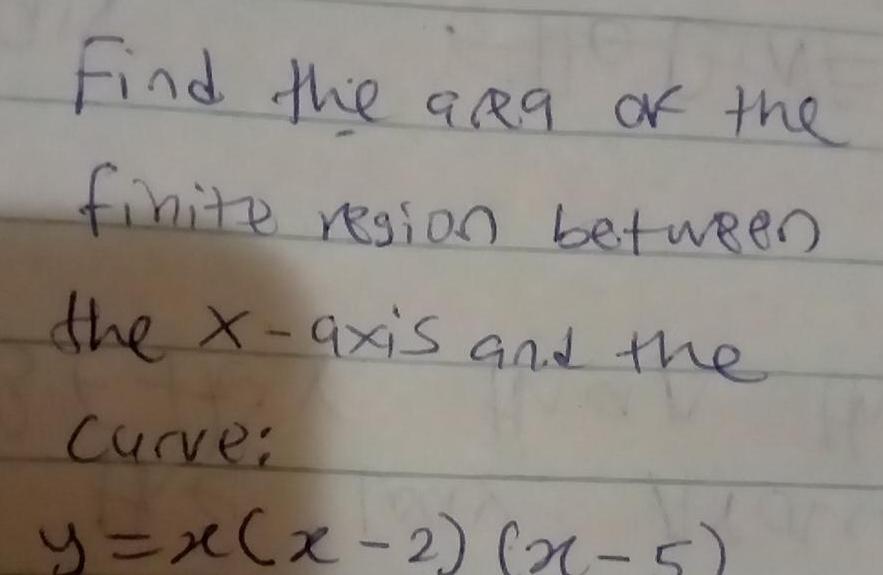
Calculus
Definite IntegralsFind the 9R9 of the finite region between the x axis and the Curve y x x 2 x 5
Calculus
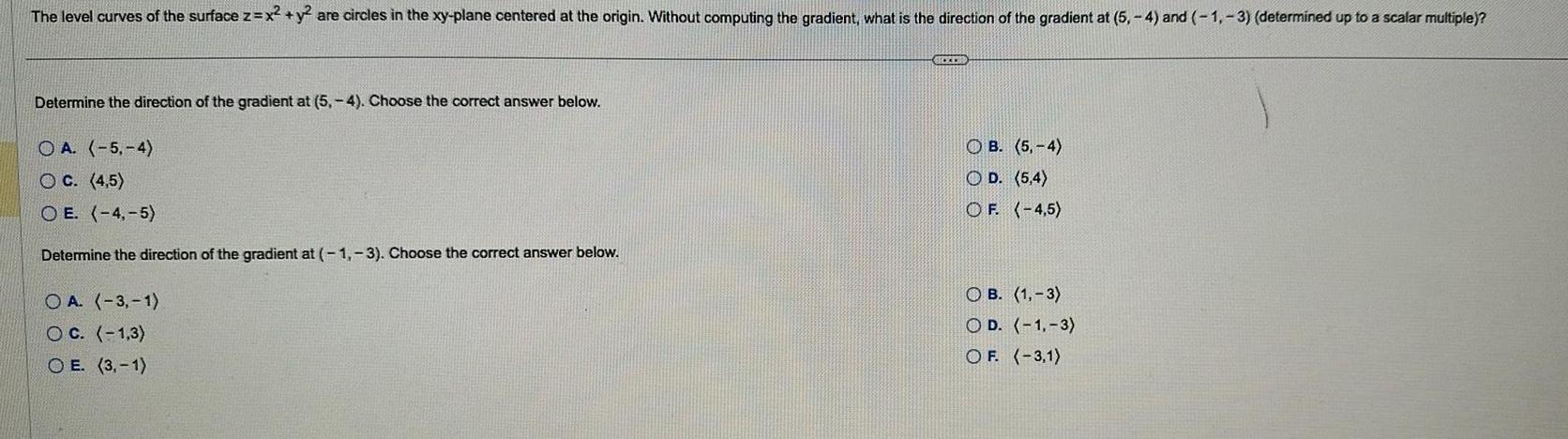
Vector CalculusThe level curves of the surface z x y are circles in the xy plane centered at the origin Without computing the gradient what is the direction of the gradient at 5 4 and 1 3 determined up to a scalar multiple Determine the direction of the gradient at 5 4 Choose the correct answer below OA 5 4 OC 4 5 OE 4 5 Determine the direction of the gradient at 1 3 Choose the correct answer below OA 3 1 OC 1 3 OE 3 1 ACCES O B 5 4 OD 5 4 OF 4 5 OB 1 3 OD 1 3 OF 3 1
Calculus
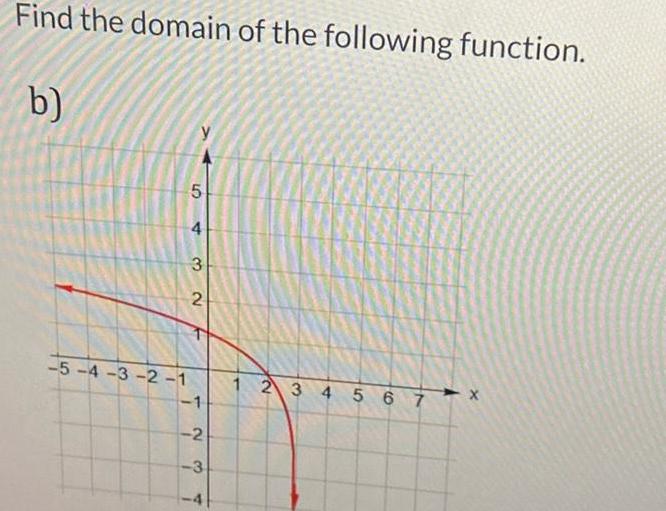
Application of derivativesFind the domain of the following function b 5 4 3 2 1 5 t 3 2 1 2 3 4 2 3 4 5 6 7
Calculus
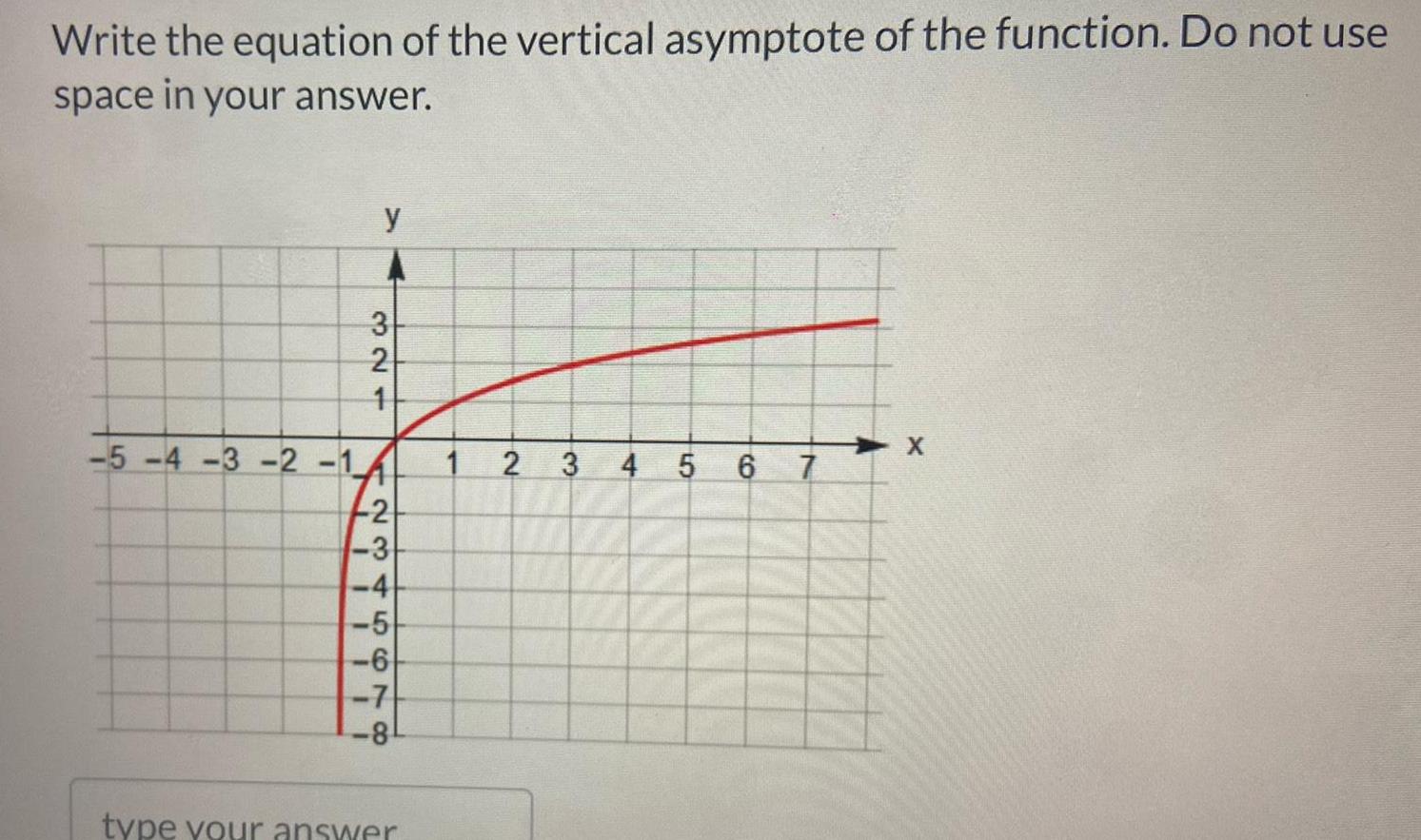
Application of derivativesWrite the equation of the vertical asymptote of the function Do not use space in your answer 5 4 3 2 1 y 3 321 2 1 2 3 4 5 6 7 8 type your answer 2 3 4 5 6 7 X
Calculus
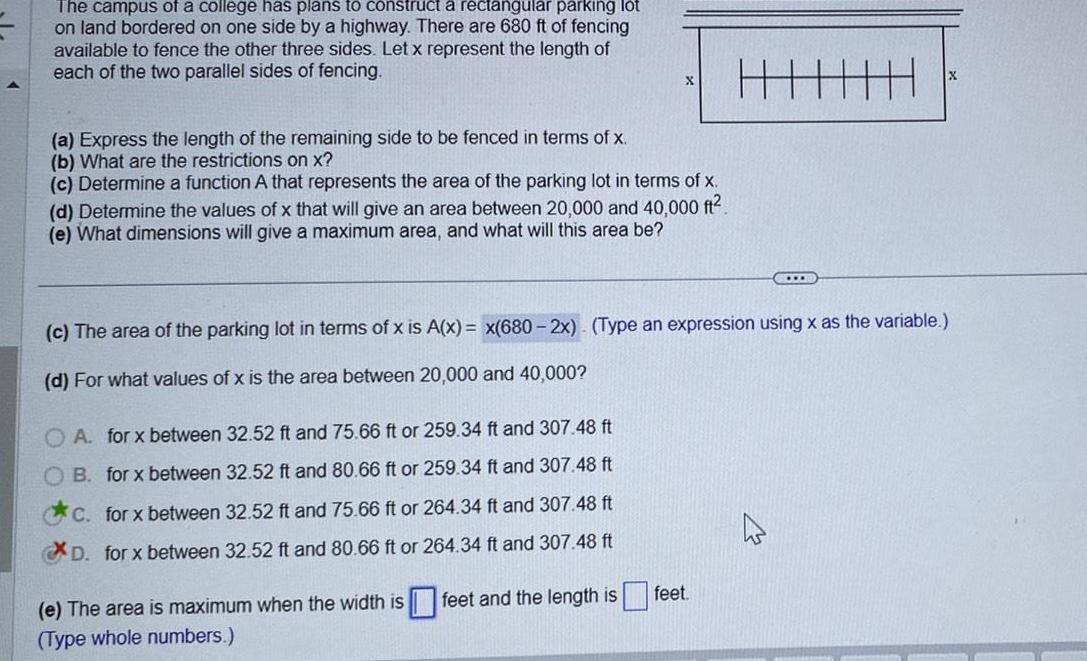
Vector CalculusThe campus of a college has plans to construct a rectangular parking lot on land bordered on one side by a highway There are 680 ft of fencing available to fence the other three sides Let x represent the length of each of the two parallel sides of fencing a Express the length of the remaining side to be fenced in terms of x b What are the restrictions on x c Determine a function A that represents the area of the parking lot in terms of x d Determine the values of x that will give an area between 20 000 and 40 000 ft e What dimensions will give a maximum area and what will this area be c The area of the parking lot in terms of x is A x x 680 2x Type an expression using x as the variable d For what values of x is the area between 20 000 and 40 000 O A for x between 32 52 ft and 75 66 ft or 259 34 ft and 307 48 ft B for x between 32 52 ft and 80 66 ft or 259 34 ft and 307 48 ft C for x between 32 52 ft and 75 66 ft or 264 34 ft and 307 48 ft D for x between 32 52 ft and 80 66 ft or 264 34 ft and 307 48 ft e The area is maximum when the width is feet and the length is Type whole numbers H feet
Calculus
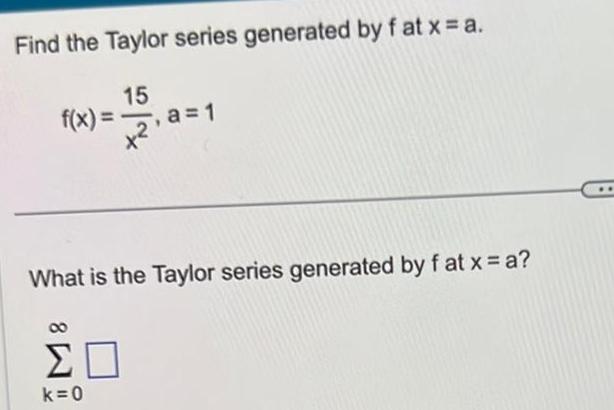
Application of derivativesFind the Taylor series generated by fat x a 15 f x a 1 2 What is the Taylor series generated by fat x a 20 k 0
Calculus
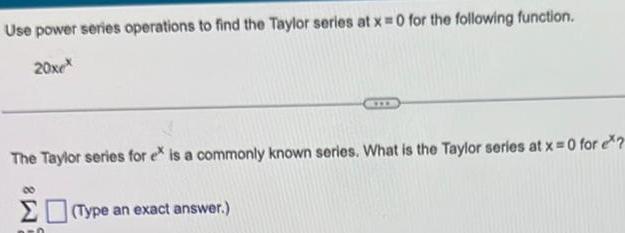
Limits & ContinuityUse power series operations to find the Taylor series at x 0 for the following function 20xex The Taylor series for ex is a commonly known series What is the Taylor series at x 0 for ex Type an exact answer

Calculus
DifferentiationFind the Maclaurin series for the given function 14X 1 X What is the Maclaurin series of f x 80 k 0 4 1 X Type an expression using k and x as the variables

Calculus
Limits & ContinuityUse substitution to find the Taylor series at x 0 of the function In 1 5x7 What is the general expression for the nth term in the Taylor series at x 0 for In 1 5x7 O n 1
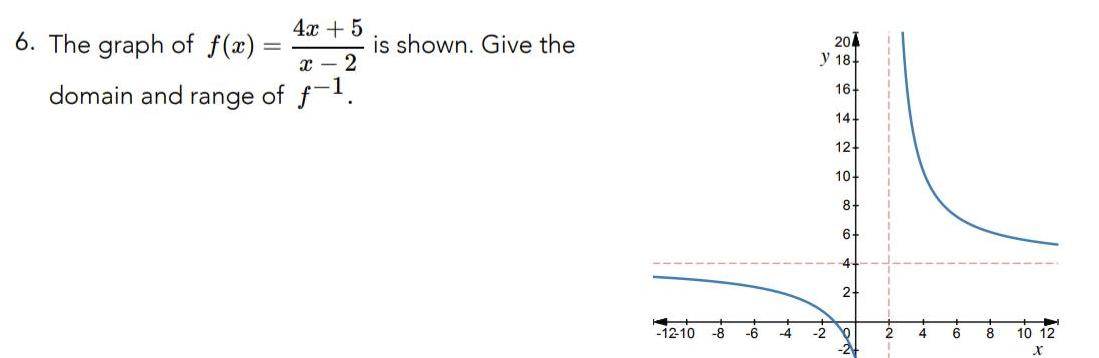
Calculus
Limits & Continuity6 The graph of f x 4x 5 x 2 domain and range of f 1 is shown Give the 12 10 8 6 4 204 y 18 2 16 14 12 10 8 6 2 10 2 2 4 6 8 10 12 X
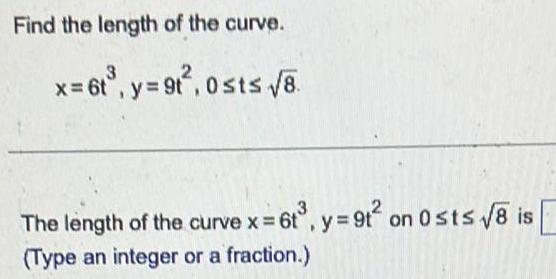
Calculus
Application of derivativesFind the length of the curve x 6t y 9t 0sts 8 The length of the curve x 6t y 9t on 0sts 8 is Type an integer or a fraction

Calculus
Application of derivativesse a graphing utility to graph each function in the interval 0 27 y 5 cos x y 5e x 5x 5 a Write an equation whose solutions are the points of intersection of the graphs b Use the intersect feature of the graphing utility to find the points of intersection to four decimal places Enter the point of intersection whose x coordinate is within the interval there is no solution enter NO SOLUTION x y x

Calculus
DifferentiationUse a graphing utility to approximate the solutions of the equation in the interval 0 2x Enter your answers as a comma separated list Round your answers to four decimal places sin x cos x X
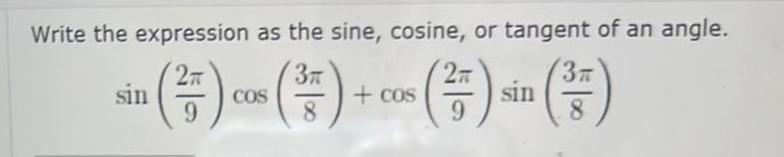
Calculus
Application of derivativesWrite the expression as the sine cosine or tangent of an angle 3T COS 57 COS 7 cos 9 8 sin sin

Calculus
Application of derivativesYou and a friend are riding your bikes to a restaurant that you think is east and that your friend thinks is north You both leave from the same starting point with you riding 16 miles per hour east and your friend riding 12 miles per hour north After you travel 4 miles at what rate is the distance between you changing Do not include units in your answer Provide your answer below

Calculus
Application of derivativesYou are tasked with constructing a rectangular box with a square base an open top and a volume of 184 in Determine what the dimensions of the box should be to minimize the surface area of the box What is the minimum surface area Keep your answer in radical form and omit units
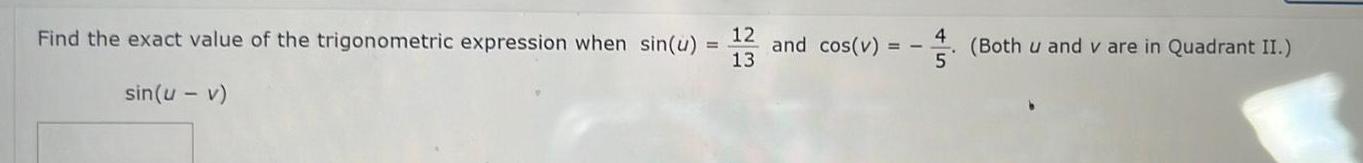
Calculus
DifferentiationFind the exact value of the trigonometric expression when sin u sin u v 12 and cos v 13 4 5 Both u and v are in Quadrant II
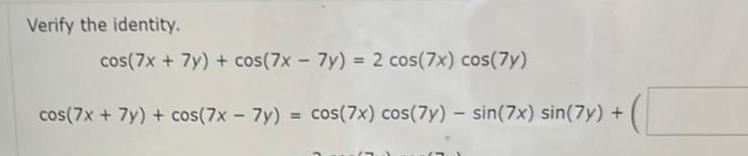
Calculus
Application of derivativesVerify the identity cos 7x 7y cos 7x 7y 2 cos 7x cos 7y cos 7x 7y cos 7x 7y cos 7x cos 7y 63 13 sin 7x sin 7y

Calculus
Application of derivativesFind the exact value of the expression tan 25 tan 110 1 tan 25 tan 110

Calculus
Application of derivativesFind the exact values of the sine cosine and tangent of the angle 75 sin 75 cos 75 tan 75

Calculus
DifferentiationFind the exact values of the sine cosine and tangent of the angle 5TT 12 sin 512 5T Cos tan 5TT 12 5TT 12 11 11 11

Calculus
Application of derivativesA 10 foot ladder is leaning against a wall If the top of the ladder slides down the wall at a rate of 2 feet per second how fast is the bottom of the ladder moving along the ground when the bottom of the ladder is 5 feet from the wall Simplify your answer as much as possible and do not include units Give an exact answer Provide your answer below

Calculus
Differential equationsUsing the trapezium rule with eight ordinates at x 3 2 1 0 1 2 3 and 4 calculate correct to 3 decimal places 6x an approximate value of 2 dx 3 WAEC

Calculus
Vector CalculusSolve the multiple angle equation Enter your answers as a comma separated list Let n be any integer sin 7x X 3 2

Calculus
Application of derivativesUse a graphing utility to approximate the solutions to three decimal places of the equation in the given interval Enter your answers as a comma separated list 6 sec x tan x 9 0 7 7 2 X

Calculus
Application of derivativesQuestion Beginning 145 miles directly west of the city of Johnstown a boat travels due north If the boat is travelling at a speed of 47 miles per hour determine the rate of change of the distance between Johnstown and the boat when the boat has been travelling for 64 miles Do not include units in your answer and round to the nearest hundredth Provide your answer below
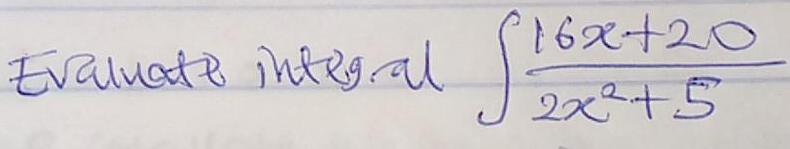

Calculus
Application of derivativesQuestion Beginning 145 miles directly south of the city of Hartville a car travels due west If the car is travelling at a speed of 42 m per hour determine the rate of change of the distance between Hartville and the car when the car has been travelling for

Calculus
Vector CalculusBeginning 145 miles directly south of the city of Hartville a car travels due west If the car is travelling at a speed of 42 miles per hour determine the rate of change of the distance between Hartville and the car when the car has been travelling for 55 miles Do not include units in your answer and round to the nearest hundredth Provide your answer below

Calculus
Application of derivativesA boat starts off 23 miles directly east from the city of Uniontown It travels due south at a speed of 41 miles per hour Let 0 represent the angle measured from due east to the direction ray pointing from Uniontown to the boat After travelling 49 miles how fast in radians per hour is 0 changing Submit an exact answer in fractional form Provide your answer below I

Calculus
Application of derivativesA rectangular container with a square base an open top and a volume of 4 000 cm is to be made What is the minimum surface area for the container Enter only the minimum surface area and do not include units in your answer

Calculus
Application of derivativesQuestion A boat is travelling due south at a speed of 53 miles per hour If the boat started off 29 miles directly west of the city of Johnstown how fast in radians per hour is the angle opposite the southward path 0 changing when the boat has travelled 23 miles Submit an exact answer in fractional form Provide your answer below
Calculus
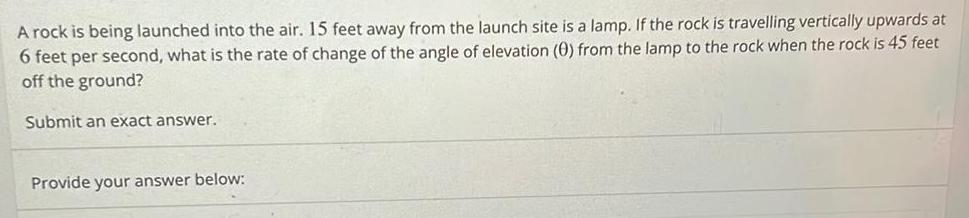
Application of derivativesA rock is being launched into the air 15 feet away from the launch site is a lamp If the rock is travelling vertically upwards at 6 feet per second what is the rate of change of the angle of elevation 0 from the lamp to the rock when the rock is 45 feet off the ground Submit an exact answer Provide your answer below

Calculus
Limits & ContinuityA zoo needs to build a rectangular enclosure that is made up of a 15 foot brick retaining wall on one side and a 10 foot chain link fence topping a two foot high brick wall on the other three sides The brick retaining wall costs 280 dollars per foot and the chain link brick fence costs about 73 per foot What dimensions will minimize the cost to build an enclosure that holds an area of 1900 square feet The brick retaining wall will be about feet long The chain link fence just one of the sides adjacent to the brick wall not opposite will be about feet long

Calculus
Application of derivativesA lamp is placed on the ground at a distance of 17 feet from the point at which a rocket will be launched into the air If the rocket travels straight up at a rate of 7 feet per second determine the rate of change of the angle of elevation 0 from the lamp to the rocket when the rocket is at a height of 43 feet Submit an exact answer in fractional form Provide your answer below

Calculus
Application of derivativesA company plans to manufacture a rectangular box with a square base an open top and a 3 volume of 246 in The cost of the material for the base is 0 2 cents per square inch and the cost of the material for the sides is 0 3 cents per square inch Determine the dimensions of the box that will minimize the cost of manufacturing it What is the minimum cost Round any calculations and the final answer to the nearest hundredth if necessary

Calculus
Application of derivativesA window is composed of a semicircle placed on top of a rectangle If you have 40 feet of window framing materials for the frame all around the rectangle and all around the semicircle as pictured below what is the maximum size of the window you can create a The radius of the semicircle portion of the maximum size window is r b The dimensions of the rectangular portion of the maximum size window are feet help numbers feet enter a comma separated list help numbers

Calculus
Application of derivativesAn airplane is flying at an altitude of 5 mi on a straight path that will take it over a radar tracking station If the distance s between the plane and the radar station is decreasing at a rate of 380 mph when s 8 what is the speed of the plane Keep your answer in rational form and omit units Provide your answer below


Calculus
Application of derivativesA company plans to manufacture a rectangular container with a square base an open top and a volume of 2 916 in Determine the dimensions of the container that will minimize the surface area What is the minimum surface area Enter only the minimum surface area and do not include units in your answer Provide your answer below
Calculus
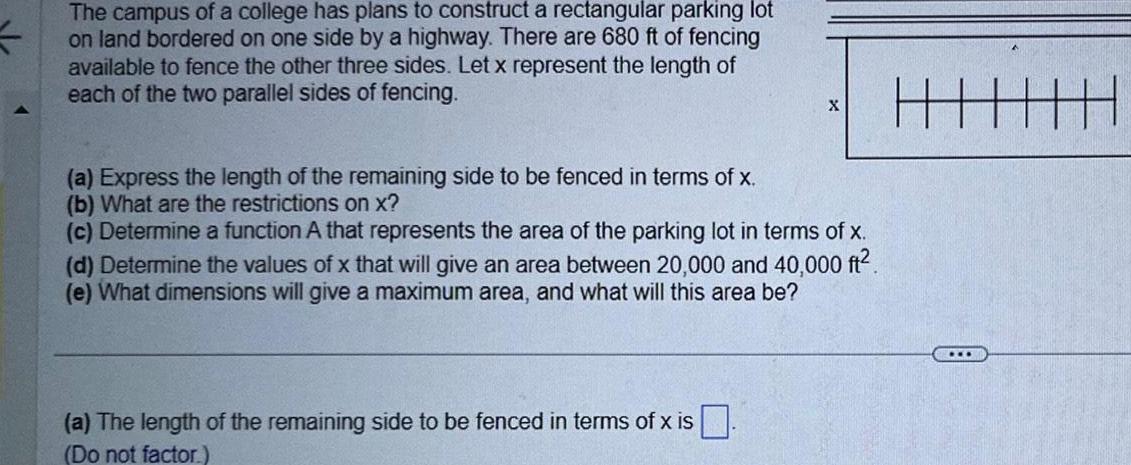
Limits & ContinuityThe campus of a college has plans to construct a rectangular parking lot on land bordered on one side by a highway There are 680 ft of fencing available to fence the other three sides Let x represent the length of each of the two parallel sides of fencing a Express the length of the remaining side to be fenced in terms of x b What are the restrictions on x X c Determine a function A that represents the area of the parking lot in terms of x d Determine the values of x that will give an area between 20 000 and 40 000 ft e What dimensions will give a maximum area and what will this area be a The length of the remaining side to be fenced in terms of x is Do not factor HH

Calculus
Application of derivativesThe cost for producing a widgets is given by C z 0 032 0 62 150z with 0 x 100 Determine the production level with the lowest average cost per widget and find the minimum average cost per widget The production level with the lowest average cost is widgets The minimum average cost per widget is

Calculus
Application of derivativesTwo poles are connected by a wire that is also connected to the ground The first pole is 16 ft tall and the second pole is 22 ft tall There is a distance of 38 ft between the two poles Where should the wire be anchored to the ground to minimize the amount of wire needed The wire should be anchored to the ground at a distance of wire feet from the pole labelled A in the diagram above in order to minimize the length of the
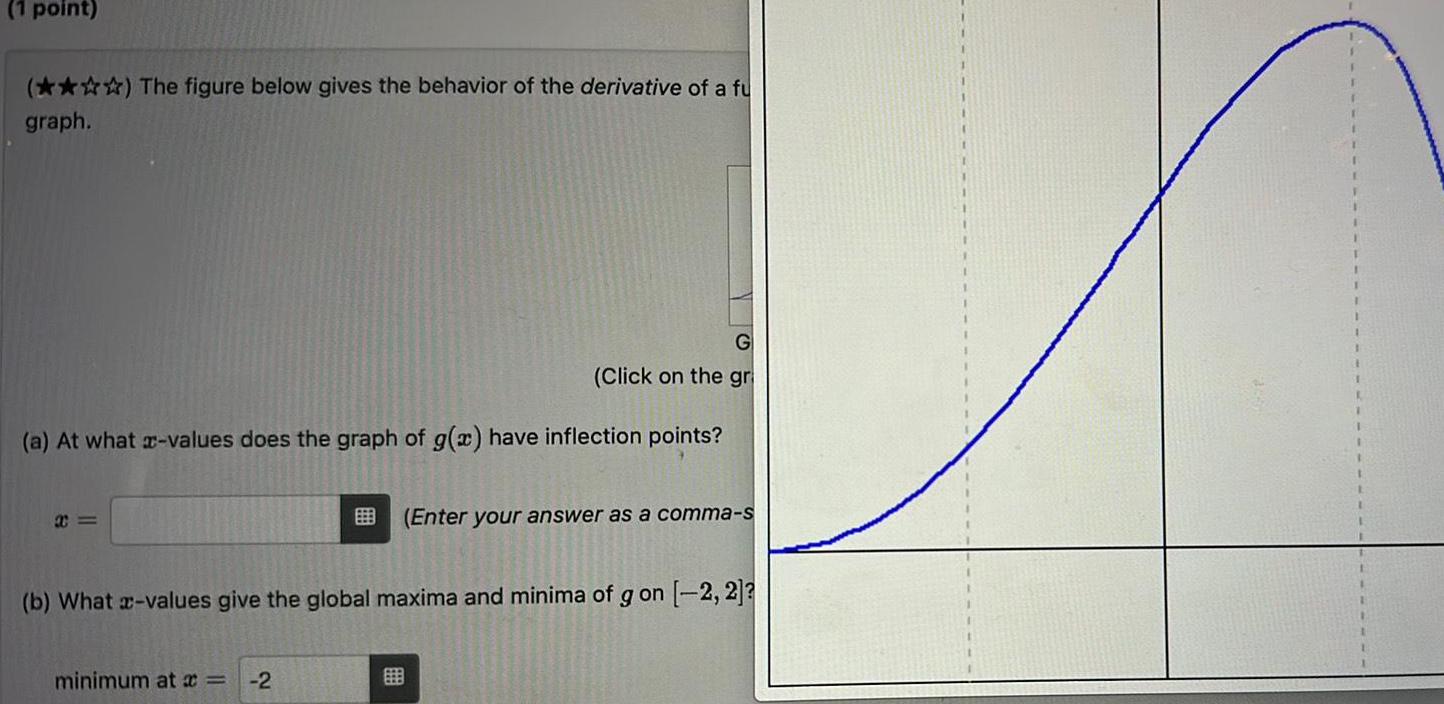
Calculus
Application of derivatives1 point The figure below gives the behavior of the derivative of a fu graph G Click on the gr a At what x values does the graph of g x have inflection points b What x values give the global maxima and minima of g on 2 2 minimum at x 2 Enter your answer as a comma s E
Calculus
Application of derivativesA rectangular box is going to be made with a volume of 274 cm The base of the box will be a square and the top will be open The cost of the material for the base is 0 3 cents per square centimeter and the cost of the material for the sides is 0 1 cents per square centimeter Determine the dimensions of the box that will minimize the cost of manufacturing it What is the minimum cost Round any calculations and the final answer to the nearest hundredth if necessary

Calculus
Application of derivativesTo carry a suitcase on an airplane with a certain airline the length width height must not exceed 61 inches Part 1 Assuming the base is a square find a formula for the maximum volume that depends only on the height h in Part 2 What height allows you to have the largest volume
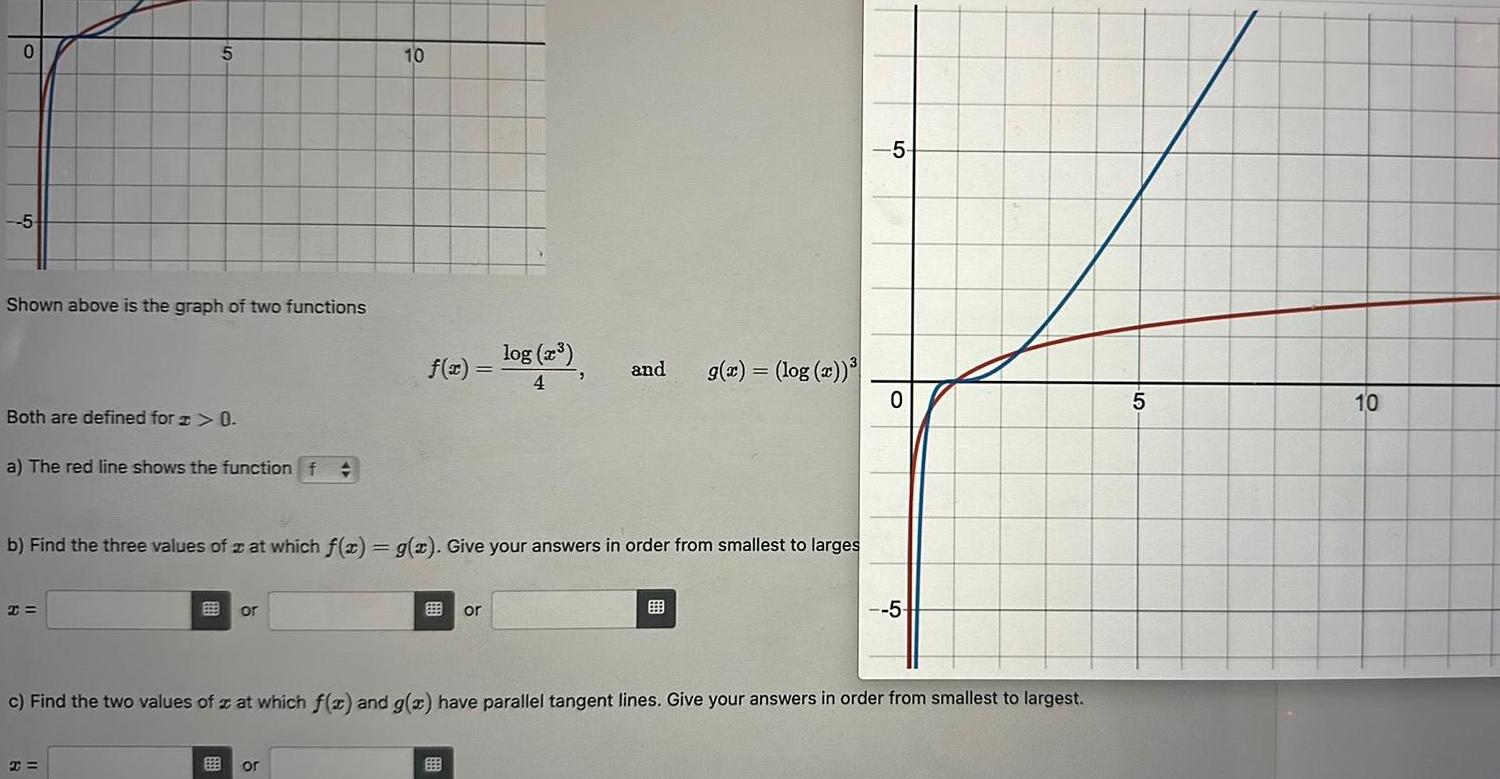
Calculus
Application of derivatives0 5 Shown above is the graph of two functions 5 Both are defined for x 0 a The red line shows the function f x or 10 b Find the three values of at which f x g x Give your answers in order from smallest to larges f x log x 4 or 3 or and g x log x 5 0 c Find the two values of x at which f x and g x have parallel tangent lines Give your answers in order from smallest to largest 5 5 10
Calculus
Application of derivativesNote If you are asked for value s give your answer as a single value e g 17 or a comma separated list e g 1 2 3 or NONE If you are asked for an interval give your answer in interval notation Type INF for oo and INF for 00 Suppose that f x x 3x a List the x values of all critical points of f x 0 9 4 B Use interval notation to indicate where f x is increasing A function is increasing if larger x values give larger y values Don t include points where the function changes from increasing to decreasing or from decreasing to increasing Increasing for a in 9 4 Inf C Use interval notation to indicate where f x is decreasing A function is decreasing if larger x values give smaller y values Don t include points where the function changes from increasing to decreasing or from decreasing to increasing Decreasing for a in D List the x values of all local maxima of f x values of local maxima none E List the values of all local minima of f x