Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
Application of derivativesSuppose that the elasticity of demand at a given price level is E p 0 8 What does that mean Select both the correct answer to elastic unit or inelastic as well as what the company should do to increase revenue Since 0 E p 1 demand is inelastic The company should lower prices to raise revenue The company should raise prices to raise revenue Since 0 E p 1 demand is elastic Since 0 E p 1 demand is unit The company should leave prices alone as the revenue is currently maximized

Calculus
DifferentiationDetermine where f x 6x5 40x 120 is increasing Select all that apply Hint Use a sign chart for the first derivative 2 2 0 2 0 0 2 DE CORRESA 19Aumar HNSTORERNA64 TERMINE ANCHEWIN


Calculus
Application of derivativesa Evaluate the Riemann sum for f x 1 x 1 x 2 with four terms taking the sample points to be right end points Give your answer correct to six decimal places Explain what the Riemann sum represents with the aid of a sketch b Repeat part a with midpoints as the sample points

Calculus
Definite Integralsing delmes a one to one function find its inverse If not write Not one to one 3 3 4 3 5 7 6 5 OA Not one to one OB 3 3 5 7 5 4 OC 3 5 3 7 5 4 OD 3 3 4 7 5 5

Calculus
Limits & Continuity6 2 x 7 X 2 OA OB O C O D 13 1 2 710 125 00 U 13 7 2 12 00 13 1 7 210 125 00 U 13 27 12 00 U


Calculus
Limits & ContinuityThe horizontal asymptote is y 5 OA OB OC OD 5 f x x 5 f x x 5 X 9 f x 5x 1 x 9 5x X 9

Calculus
Application of derivativest MY NOTES A drug response curve describes the level of medication in the bloodstream after a drug is administered A surge function S t AtPe kt where t 0 is often used to model the response curve reflecting an initial surge in the drug level and then a more gradual decline If for a particular drug A 0 03 p 4 k 0 08 and t is measured in minutes estimate the times t corresponding to the inflection points Round your answers to two decimal places min smaller value min larger value t PRACTICE ANOTHER

Calculus
Limits & ContinuityGive the equations of any asymptotes of the type specified for the graph of the rationa 2x 11 x 2x 15 f x vertical OA x 3 x 5 OB x 3 x 5 OC y 3 y 5 OD y 2

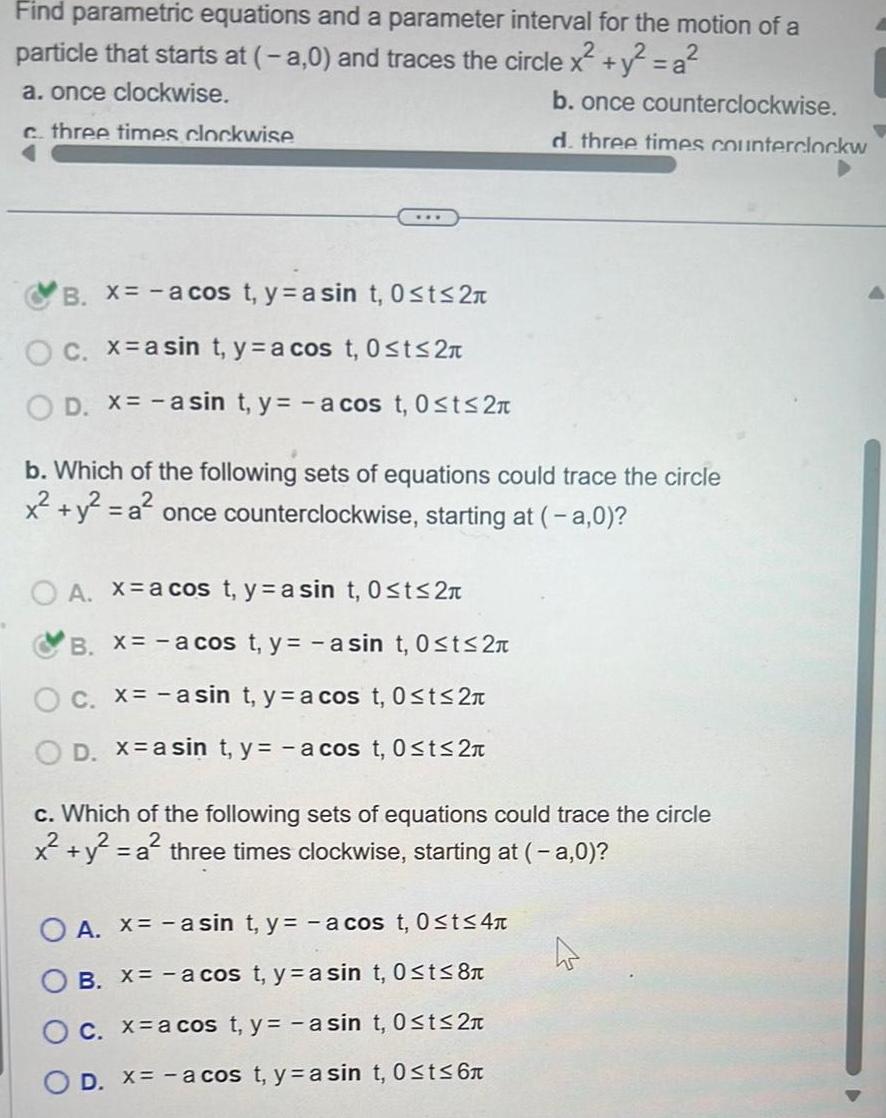
Calculus
Application of derivativesFind parametric equations and a parameter interval for the motion of a particle that starts at a 0 and traces the circle x y a a once clockwise b once counterclockwise c three times clockwise d three times counterclockw B x a cos t y asin t 0 t 2 O c x a sin t y a cos t 0 t 2 D x asin t y a cos t 0 t 2n b Which of the following sets of equations could trace the circle x y a once counterclockwise starting at a 0 OA xa cos t y a sin t 0 t 2 B x a cos t y asin t 0 ts 2 C x a sin t ya cos t 0 t 2 D x a sint y a cos t 0 t 2 c Which of the following sets of equations could trace the circle x y a a three times clockwise starting at a 0 O A x asin t y a cos t 0 t 4 B X a cos t y a sin t 0 t 8 C x a cos t y asin t 0 t 2 D x a cos t y a sin t 0 t 6 4 D

Calculus
Application of derivatives5 a Estimate the prea under the graph of f x 1 x from x 1 to x 2 using three rectangles and right end points Then improve your estimate by using six rect angles Sketch the curve and the approximating rectangles b Repeat part a using left endpoints c Repeat part a using midpoints d From your sketches in parts a c which estimate appears to be the most accurate

Calculus
Application of derivativesWhich of the following would represent an approximation of R 51 using information from R x OR 51 R 51 R 51 OR 51 R 50 OR 51 R 50 OR 51 R 50 R 50

Calculus
Application of derivativesIf h x f g x and f 1 7 f 1 10 g 1 1 and g 1 5 find h 1 O 14 ONot enough information O 350 O 50 O 35

Calculus
Application of derivativesIf C x 3000 10x 0 05x then find the marginal average cost function Cave x O Cave x 10 0 1x 3000 O O O Cave x Cave Cave x Cave x OC 3000 C 10 x 0 05 10 0 05x 0 1 3000 10x 0 05x
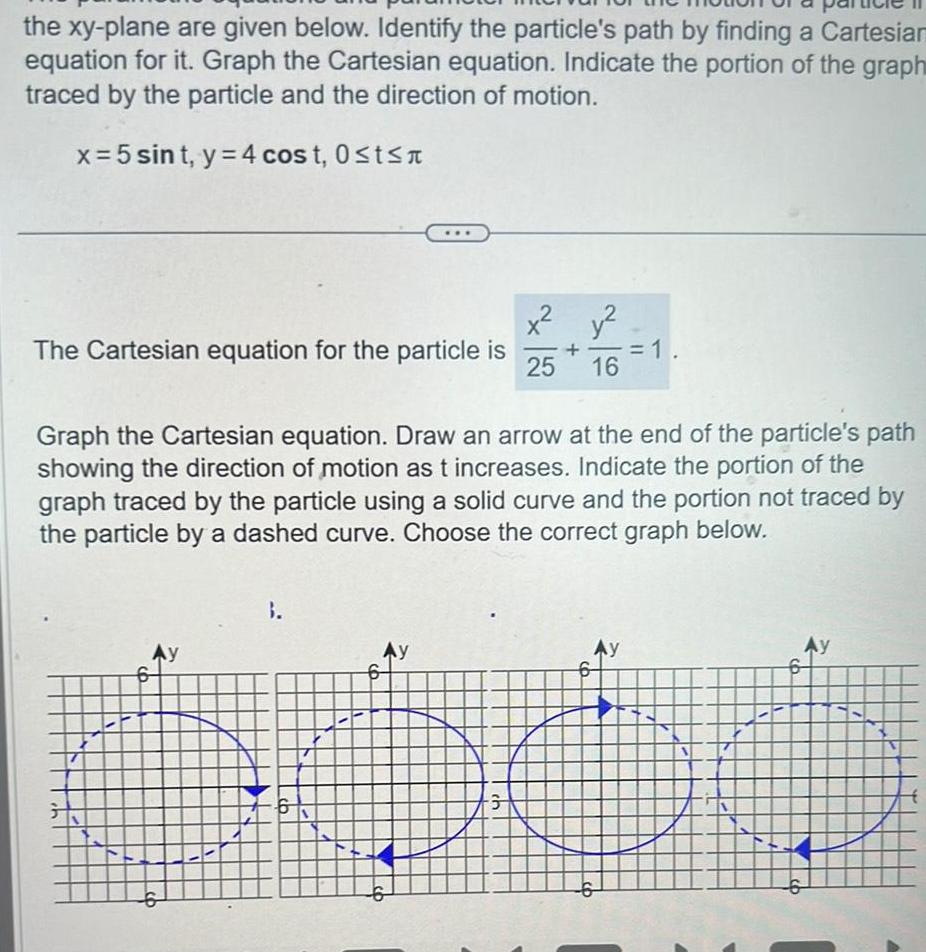
Calculus
Application of derivativesthe xy plane are given below Identify the particle s path by finding a Cartesian equation for it Graph the Cartesian equation Indicate the portion of the graph traced by the particle and the direction of motion x 5 sint y 4 cost 0 t The Cartesian equation for the particle is Ay 9 3 Graph the Cartesian equation Draw an arrow at the end of the particle s path showing the direction of motion as t increases Indicate the portion of the graph traced by the particle using a solid curve and the portion not traced by the particle by a dashed curve Choose the correct graph below Ay 6 25 ch y 16 1 Ay AY

Calculus
Differential equationsIf g x O Og x t x 3t x t x 3e3 g x g x e3x g x find and simplify g x t x 3t x e x t x 3t x e 4


Calculus
DifferentiationFind the derivative of the following 3 5 g x Og x 12a 5 5 Og x 3x 4 52 3 g x 04 g x 12 15 25 A 5 3

Calculus
Application of derivativesFind the derivative of y 3x5 4x 2 g x O None of the other choices is correct O 1524 g 2 g x 3x 4x 2 O 15244 g x g x 3x 4x 2 O 1524 4 g x O 1544 g x g x 3x 4x 2

Calculus
Application of derivativesFind parametric equations and a parameter interval for the motion of a 2 particle that starts at a 0 and traces the circle x y a a once clockwise b once counterclockwise d three times counterclockw c three times clockwise a Which of the following sets of equations could trace the circle x y a once clockwise starting at a 0 OA x a cos t y a sin t 0 t 2 B X a cos t y a sin t 0 t 2n O c x asin t y a cos t 0 t 2 O D x asin t y a cos t 0 t 2 b Which of the following sets of equations could trace the circle x y a once counterclockwise starting at a 0 OA x a cos t y a sin t 0 t 2 OB X a cos t y a sin t 0 t 2 O c x asin t y a cos t 0 t 2 D x a sin t y a cos t 0 t 2

Calculus
Application of derivativesFind a parameterization for the circle x 12 y 36 starting at the point 6 0 and moving clockwise once around the circle Find parametric equations for the circle X y 0 0 2

Calculus
Application of derivativesFind a parametrization for the curve described below the line segment with endpoints 3 3 and 2 2 Complete the pair of parametric equations using linear functions of t One possible parametrization is x t 3 y 0sts 1

Calculus
Application of derivatives2 2 2 particle that starts at a 0 and traces the circle x y a a once clockwise c three times clockwise b once counterclockwise d three times counterclockw 2 a Which of the following sets of equations could trace the circle x y once clockwise starting at a 0 OA x a cos t y a sin t 0 t 2 OB X a cos t yasin t 0 t 2 O c x asin t y a cos t 0 t 2 O D x asin t y a cos t 0 t 2

Calculus
Application of derivativesThe parametric equations and parameter interval for the motion of a particle in the xy plane are given below Identify the particle s path by finding a Cartesian equation for it Graph the Cartesian equation Indicate the portion of the graph traced by the particle and the direction of motion x 5 sint y 4 cos t 0 t n The Cartesian equation for the particle is

Calculus
Application of derivativesThe parametric equations and parameter intervals for the motion of a particle in the xy plane are given below Identify the particle s path by finding a Cartesian equation for it Graph the Cartesian equation Indicate the portion of the graph traced by the particle and the direction of motion x cos 2t y sin 2t 0stst The Cartesian equation for the particle is

Calculus
Application of derivativesThe equation below gives parametric equations and parameter intervals for the motion of a particle in the xy plane Identify the particle s path by finding a Cartesian equation for it Graph the Cartesian equation Indicate the portion of the graph traced by the particle and the direction of motion x 4t 3 y 16t t Find a Cartesian equation for the particle s path y 0

Calculus
Differential equations1 point Calculate the following for the matrix A det A 21 and A 6 21 7 21 201 2 30 302 6 21

Calculus
Application of derivativesUse the given graph of f over the interval 0 7 to find the following a The open intervals on which f is increasing Enter your answer using interval notation 0 b The open intervals on which f is decreasing Enter your answer using interval notation c The open intervals on which f is concave upward Enter your answer using interval notation d The open intervals on which f is concave downward Enter your answer using interval notation e The coordinates of the points of inflection x y smallest x value x y x y largest x value

Calculus
Definite IntegralsConsider the equation below If an answer does not exist enter DNE f x x4 8x2 7 a Find the interval on which f is increasing Enter your answer using interval notation X Find the interval on which f is decreasing Enter your answer using interval notation b Find the local minimum and maximum valu s of f local minimum value local maximum value c Find the inflection points x y x y smaller x value larger x value Find the interval on which f is concave up Enter your answer using interval notation Find the interval on which f is concave down Enter your answer using interval notation

Calculus
Definite IntegralsFind the limit Use l Hospital s Rule where appropriate If there is a more elementary method consider using it x2x lim x 0 2x 1 1 log 2 X

Calculus
Differential equationsGiven that lim f x 0 x a b lim g x 0 x a d lim p x x a 00 evaluate the limits below where possible If a limit is indeterminate enter INDETERMINATE a f x lim x a g x f x lim x a P x h x lim x a p x lim h x 1 x a lim P x x a 9 x lim g x 0 x a

Calculus
Application of derivativesFind the limit Use l Hospital s Rule if appropriate If there is a more elementary method consider using it sin 4x lim x 0 tan 7x Submit Answer

Calculus
Differentiationf x 0 if x 0 or 2 x 4 f x 0 if 0 x 2 orx 4 f x 0 if 1 x 3 f x 0 if x 1 orx 3 2

Calculus
DifferentiationSuppose f is continuous on a If f 1 0 and f 1 1 what can you say about f At x 1 f has a local maximum At x 1 f has a local minimum At x 1 f has neither a maximum nor a minimum More information is needed to determine if f has a maximum or minimum at x 1 b If f 3 0 and f 3 0 what can you say about f At x 3 f has a local maximum At x 3 f has a local minimum At x 3 f has neither a maximum nor a minimum More information is needed to determine if f has a maximum or minimum at x 3

Calculus
Application of derivativesConsider the equation below f x 2x 3x 72x a Find the interval on which f is increasing Enter your answer in interval notation Find the interval on which f is decreasing Enter your answer in interval notation b Find the local minimum and maximum values of f local minimum local maximum c Find the inflection point x y Find the interval on which f is concave up Enter your answer in interval notation Find the interval on which fis concave down Enter your answer in interval notation

Calculus
DifferentiationLet f t be the temperature at time t where you live and suppose that at time t 1 you feel uncomfortably hot What happens to the temperature in each case a f 1 2 f 1 2 The temperature is increasing and the rate of increase is increasing O The temperature is increasing but the rate of increase is decreasing O The temperature is decreasing but the rate of change is increasing becoming less negative The temperature is decreasing and the rate of change is decreasing becoming more negative b f 1 2 f 1 2 O The temperature is increasing and the rate of increase is increasing The temperature is increasing but the rate of increase is decreasing The temperature is decreasing but the rate of change is increasing becoming less negative The temperature is decreasing and the rate of change is decreasing becoming more negative c d f 1 2 f 1 2 The temperature is increasing and the rate of increase is increasing The temperature is increasing but the rate of increase is decreasing The temperature is decreasing but the rate of change is increasing becoming less negative The temperature is decreasing and the rate of change is decreasing becoming more negative f 1 2 F 1 2 The temperature is increasing and the rate of increase is increasing MY NO The temperature is increasing but the rate of increase is decreasing The temperature is decreasing but the rate of change is increasing becoming less negative The temperature is decreasing and the rate of change is decreasing becoming more negative

Calculus
Application of derivativesFind the limit Use l Hospital s Rule where appropriate If there is a more elementary method consider using it x2x lim x 0 2x 1

Calculus
Definite IntegralsFind the limit Use l Hospital s Rule appropriate If there is a more elementary method consider using it 18 3 In x 3x X 1 X 1


Calculus
Differentiation6 Find every number c that satisfies the conclusion of the Mean Value Theorem for the function f x x 4x x on the interval 0 1

Calculus
Application of derivatives3 Below is the graph of f x x 5x 6x 2 On the interval 0 3 determine the maximum and minimum value of the slope of the graph i e the maximum and minimum values of g x f x 3 2 1 Y 0 1 2 X 3

Calculus
Definite Integrals8 T F with justification The graph of the semicircle on 1 1 below fits the hypotheses of the Mean Value Theorem 1 Y 1 X

Calculus
Definite Integrals4 T F with justification If f x is a differentiable function on a b and f x has a local maximum or minimum value at x c in a b then f c 0 I 5 T F with justification If f x is a differentiable function on a b and f c 0 for a number c in a b then f x has a local maximum or minimum value at x C

Calculus
Application of derivatives2 Use calculus to find the absolute maximum and minimum values of the following func tions on the given intervals Give your answers exactly and show supporting work a f x x 2x x 1 on 0 1 b x 2 on 1 3 T

Calculus
Differentiation4 1 Maximum and Minimum Values 1 For the following functions find all critical numbers exactly a f x x5 2x T b f x x 2 sin x for 0 x 2

Calculus
Limits & ContinuityPlot a shape as your original figure Object 20pts THE SHAPE SHOULD HAVE AT LEAST 6 POINTS o Dilate the figure using three different scale factors of your choice 2 enlargements 10 pts 1 reductions 10 pts each o Label each object and image 10pts o Write coordinates for each shape 20 pts Also create a horizontal vertical stretch 20 pts of your ORIGINAL figure 10 pts each Color each dilation a different color 5 pts

Calculus
Application of derivatives2 a Use six rectangles to find estimates of each type for the 12 area under the given graph of f from x i Lo sample points are left endpoints ii Ro sample points are right endpoints iii M6 sample points are midpoints b Is Lo an underestimate or overestimate of the true area c Is R an underestimate or overestimate of the true area d Which of the numbers L6 R6 or M6 gives the best estimate Explain YA 8 4 0 4 y f x 8 0 to x 12 x

Calculus
Limits & Continuityerpetual inventory using LIFO Beginning inventory purchases and sales for Item 88 HX are as follows 94 units 31 75 units July 1 Inventory July 8 Sale July 15 Purchase 104 units 33 July 27 Sale 87 units Assuming a perpetual inventory system and using the last in first out LIFO method determine a the cost of goods sold on July 27 and b the inventory on July a Cost of goods sold on July 27 b Inventory on July 31