Geometry Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Geometry
2D Geometry1 5 cm 3 cm 4 10 cm 4 cm a can of paint covers 6cm how many cans of paint would be needed to cover the prism in 1

Geometry
2D GeometryYOU 2 The following glass is filled 25 of the way with water Determine the volume below 4 cm 2 cm



Geometry
AreaQV is tangent to circle O at point Q and QB is a secant line If mQFB 252 findm BQV F B V


Geometry
Area1 A roll of wrapping paper covers 25 cm Imani plans to wrap the cylinder below in paper How mal rolls of paper will Imani need to purchase 4 cm 2 cm

Geometry
AreaYOU DO ROUND 2 2 Determine the surface area of the hemisphere below with a diameter of 14 in to the nearest 14 in lberedt sid

Geometry
2D Geometry3 1 can of paint covers 100 cm In the cylinder r 8 cm and h 20 cm Determine paint cans needed to paint both objects 12 6 5 h


Geometry
AreaSally had just got her license and the first night her parents said she could drive she came home and her little dog ran in front of her To avoid her dog she smashed into the side of the house After everyone was determined to be OK she had the fun of repairing the damage to the house She offered to paint the side of the house for her parents Her parents left it up to her to buy the paint and do all the work Using her amazing Algebra 2 skills she thought she d calculate what to buy The first step was to determine how much paint she would need First she needed to determine the surface area of the side of the house in order to estimate the number of gallons of paint she would need She knew the top of the house was an isosceles triangle She figured she could climb on a ladder to measure the angle between the pitch of the roof and the wall and the rest was pretty easy Using composite figures and trigonometry she calculated the area of the side of the house Image of the house with measurements Next she went to the local hardware store and learned that there are many different types of paint So she created a table to compare the different kinds and determine which would be best Assignment 1 Calculate the square area of the side of the house Image of the house with measurements 2 Create your own table comparing the prices of paint Choose three types of paint Some might contain primer a substance that helps the paint stick better and appear darker These are often more expensive but that would be one less coat of paint You can use this sample table or make your own 3 Summarize the plan of action that Sally should take Type of Paint Behr Sherwin Williams Glidden no Price gallon Coverage 200 400 350 350 Surface Area of the side of the House gallons for one coat Number of coats Total of gallons Cost

Geometry
3D GeometryIn the diagram QR ST 144 CU 3x and CV 6x 21 a Find CU 3x b Find the radius of OC 9x S W GF

Geometry
Solution of trianglesa right triangle has an area of 20 square centimetes and a hypotenus of 10 cm what are the exact lengths of the legs of the right triangle

Geometry
Solution of trianglesIn triangle ABC shown the side from A to B is 50m long while ZABC 1000 and ZACB 300 Find the measure of angle BAC

Geometry
3D GeometryIn the figure below AD 140 and BC 26 What is the measure of ZAED A 140 26 B C E D

Geometry
Heights & DistancesA cruise ship maintains a speed of 23 knots nautical miles per hour sailing from San Juan to Barbados a distance of 600 nautical miles To avoid a tropical storm the captain heads out of San Juan at a direction of 33 off a direct heading to Barbados The captain maintains the 23 knot speed for 8 hours after which time the path to Barbados becomes clear of storms a Through what angle should the captain turn to head directly to Barbados b Once the turn is made how long will it be before the ship reaches Barbados if the same 23 knot speed is maintained a The captain should head through an angle of Do not round until the final answer Then round to one decimal place as needed Barbados 33 San Juan

Geometry
2D GeometryThis Venn diagram shows sports played by 10 students Jada Gabby OA 3 0 50 OB B 0 375 3 8 O C 0 60 3 OD 0 10 PLAYS BASKETBALL 0 30 Fran lan Juan Let event A The student plays basketball Let event B The student plays soccer What is P AIB Ella Mai Karl PLAYS SOCCER Mickey Marcus

Geometry
2D GeometryFind the coordinates of a point on a circle with radius 15 corresponding to an angle of 80 x y Round your answers to three decimal places

Geometry
2D GeometryQuestion 1 Points 2 If the point 9 5 is translated 6 units left and 5 units up then find the translated coordinates of the point O 3 10 O 3 10 O 3 10 O 3 10


Geometry
AreaL If MLP 17 17 what 18 is the length of LMP 131 90 O 72 O 28 90 M 41 90 72 T TU 17 JU 90 T K


Geometry
2D Geometry3 Find the volume of each solid Then list these solids in order from the one with the least volume to the one with the greatest volume Part I Give the volume of each solid Show your work A a cube with edge 5 cm B a cylinder with a radius of 4 cm and a height of 4 cm C a square pyramid with base edges 6 cm and height 6 cm D a cone with a radius 4 cm and height 9 cm E a rectangular prism with a 5 cm by 5 cm base and height 6 cm Part II list these solids in order from the one with the least volume to the one with the greatest volume

Geometry
2D Geometry4 Three balls are packaged in a cylindrical container as shown below The balls just touch the top bottom and sides of the cylinder The diameter of each ball is 13 cm a What is the volume of the cylinder Explain your method for finding the volume b What is the total volume of the three balls Explain your method for finding the total volume c What percent of the volume

Geometry
Solution of triangles1 The volumes of two similar figures are given The surface area of the smaller figure is given Find the surface area of the larger figure Show your work V 27 cm V 125 cm SA 63 in

Geometry
2D Geometry2 An ice cream vendor presses a sphere of frozen yogurt into a cone as shown below If the yogurt melts into the cone will the cone overflow Explain and show work Note The diameter of the scoop is 8 cm and the height of the cone is 8 cm 12 cm

Geometry
2D Geometry3 Eric has a trolley He wants to use that trolley to transport wooden blocks The size of the trolley is 3 960 000 square centimeters He found the wooden blocks to have a density of 0 0029 blocks per square centimeter How many total wooden blocks can he carry in the trolley

Geometry
3D Geometry2 Sarah has an eBay store She will pay for shipping for parcels that are not more than 25 kg and have a volume of 17 000 cm Sam buys an item from Sarah s store The density of his parcel is 0 002 kg cm3 the height is 25 cm the width is 18 cm and the length is 30 cm You have to calculate the mass of the parcel Does this parcel qualify for free shipping

Geometry
Coordinate system4 Cathy threw a plastic toy in the pool for her puppy But there is a problem the puppy does not like putting his face in water If the weight of the toy is more than 350 grams it will sink The density and volume of the toy is respectively 0 453 g ml 673 45 ml Will the toy sink or float

Geometry
Area1 ASU Gammage Auditorium is 75 000 square feet The population density is 0 039 people per square foot How many people can attend an event at Gammage

Geometry
3D Geometry1 One right circular cone is set inside a larger right circular cone Find the volume of the space between the cones if the diameter of the inside cone is 9 in the diameter of the outside cone is 15 in and the height of both is 8 in Round to the nearest tenth

Geometry
3D Geometry2 The two figures below are similar ALAL 10 ft 8 ft 15 ft a What is the scale factor of the first figure to the second figure If necessary simplify the ra b What is the ratio of their surface areas c What is the ratio of their volumes

Geometry
Area3 Abigail is putting juice into cone shaped containers to make popsicles She has approximately one quarter of a gallon or 58 cubic inches of juice to make the popsicles with Each container has a height of 3 inches Use the information to complete the table indicating the maximum number of popsicles that Abigail could make with 58 cubic inches of juice Radius of the Maximum Container Number of Popsicles 0 5 inch 1 inch 1 5 inch

Geometry
2D Geometry4 The volumes of two similar figures are 216 cm and 1728 cm The surface area of the larger figure is 864 cm Find the surface area of t smaller figure

Geometry
Coordinate system3 The surface areas of two similar figures are 96 in and 216 in The volume of the larger is 216 in Find the volume of the smaller figure

Geometry
Coordinate system4 The plane region is revolved completely about the y axis to sweep out a solid of revolution The solid formed is a cone Find the volume of the cone Show your work AY 10

Geometry
3D Geometry4 Use the formula SA ph 2B to find the surface area of the rectangular prism below Show your work 4 8 ft 2 2 ft 1 9 ft

Geometry
2D Geometry2 The Pyramid of Khufu is a square pyramid which had a side length of about 230 m and a height of about 147 m when it was completed The Pyramid of Khafre had a side length of about 215 m and a height of about 144 m when it was completed What was the approximate difference in the volume of the two pyramids upon completion

Geometry
Coordinate system2 An artist creates a right prism whose bases are regular pentagons He wants to paint the lateral surfaces of the prism One can of paint can cover 30 square feet How many cans of paint must he buy if the height of the prism is 15 ft and the length of each side of the pentagon is 5 ft Show your work

Geometry
2D Geometry4 6 Given Point is the midpoint of AC Point C is the midpoint of AD Prove 4AB AD Arrange the steps in order to complete the proof 1 2 3 4 G 5 Use the figure to complete the proof of the theorem 1 21 22 2 21 and 22 form a linear pair 3 21 and 22 are supplementary 4 21 and 22 are right angles If two congruent angles form a linear pair then they are right angles Given 21 22 Prove m 1 Given 2 3 4 Blank 2 Point is the midpoint of AC Point C is the midpoint of AD Given AABAD Addition AB AB AD 4 ABAD Substitution CD Definition of midpoint AC CD AD Segment Addition Postulate it is given that Z21 22 Also 2123 because these are ABBC AC All 4 BC AC AB AB AC AC AC AD Substitution Blank 1 options corresponding vertical angles Therefore 22 23 by the Transitive Property of Congruence by the Blank 1 2 OPTIONS Linear pairs are suppl Oliven If 2s are and suppl then they are right s Blank 2 options Converse of Corresponding Angles Theorem Converse of Alternate Exterior Angles Theorem that m

Geometry
2D Geometry3 A box measures 10 in wide 12 in high and 14 in deep If all surfaces are made of cardboard how much cardboard is used to make the box Show your work

Geometry
2D Geometry1 For a d use the diagram below 4 cm 4 cm 4 cm 4 cm 4 cm 4 cm 9 cm a Classify the prism b Find the lateral area of the prism c The bases are regular hexagons They are of each is about 41 6 cm Find the sum of their d Find the surface area of the prism

Geometry
3D Geometry5 Serena is drawing pictures of cross sections of the right circular cone below Which drawing cannot be a cross section of the cone 1 2 3 4

Geometry
3D GeometryQuestion 10 Points 1 Which of the following transformations carry the given regular polygon onto itself O Translation O Reflection O Dilation O None of the choices
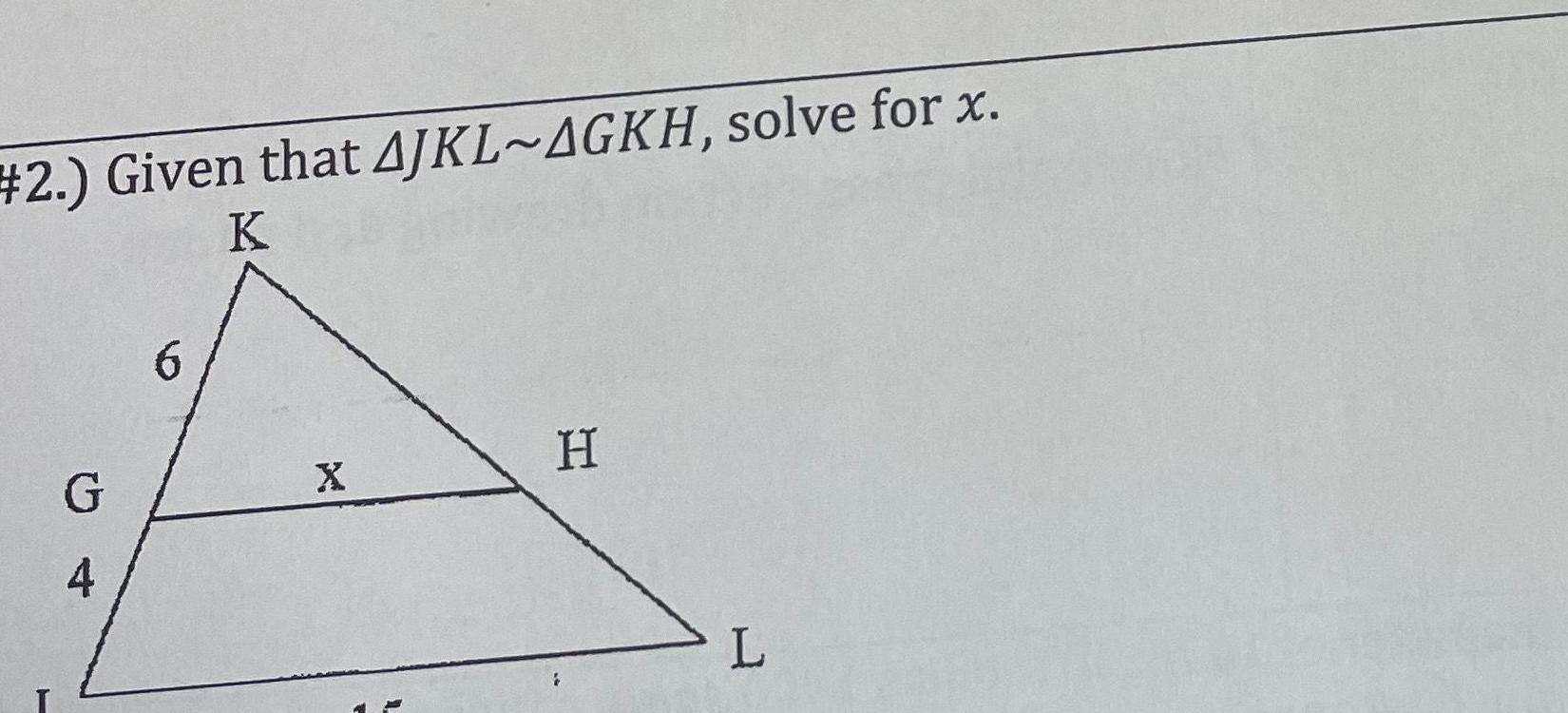

Geometry
2D GeometryQuestion 9 Points 1 Which of the following transformation carry the given regular polygon onto itself Rotation of 72 Reflection across the line of symmetry Rotation of 45 None of the above

Geometry
2D Geometry6 Draw and name the vertical and horizontal cross section for the cylinder below Vertical cross section drawing and name

Geometry
2D GeometryQuestion 5 Points 2 Identify the symmetry O Reflection symmetry O Rotational symmetry Both

Geometry
3D Geometry3 Determine the surface area of the sphere below with a radius of 5 Express you 5

Geometry
2D Geometrysson Posttest Points 2 Question 6 Which of the following transformations carry this regular polygon onto itself O rotation of 60 clockwise Orotation of 45 clockwise Orotation of 75 clockwise the line symmetry