Geometry Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Geometry
Heights & Distancesa softball player named Jen You were d to find the probability of Jen getting at least 12 hits in her next 20 at bats when she has a batting average 40 Because we have the technology to find binomial probabilities and their sums quickly we could have Pix2121 1 Pix 11 1 0 53435 0 0565 where we fnd Ply 11 0 9435 by using the graphing ator tincion biomatf2004 or prestaly some other form of technology Suppose weddit het hat would be bound the 10565 answer quickly se the Normal Distribution as an approximation for the Binomial Distribution Find the mean and standard deviation of the binomial distribution where X8 20 0 4 Mean Standard Deviation b Using the mean and standard deviation fr a Normal Distribution find the z score that
Geometry
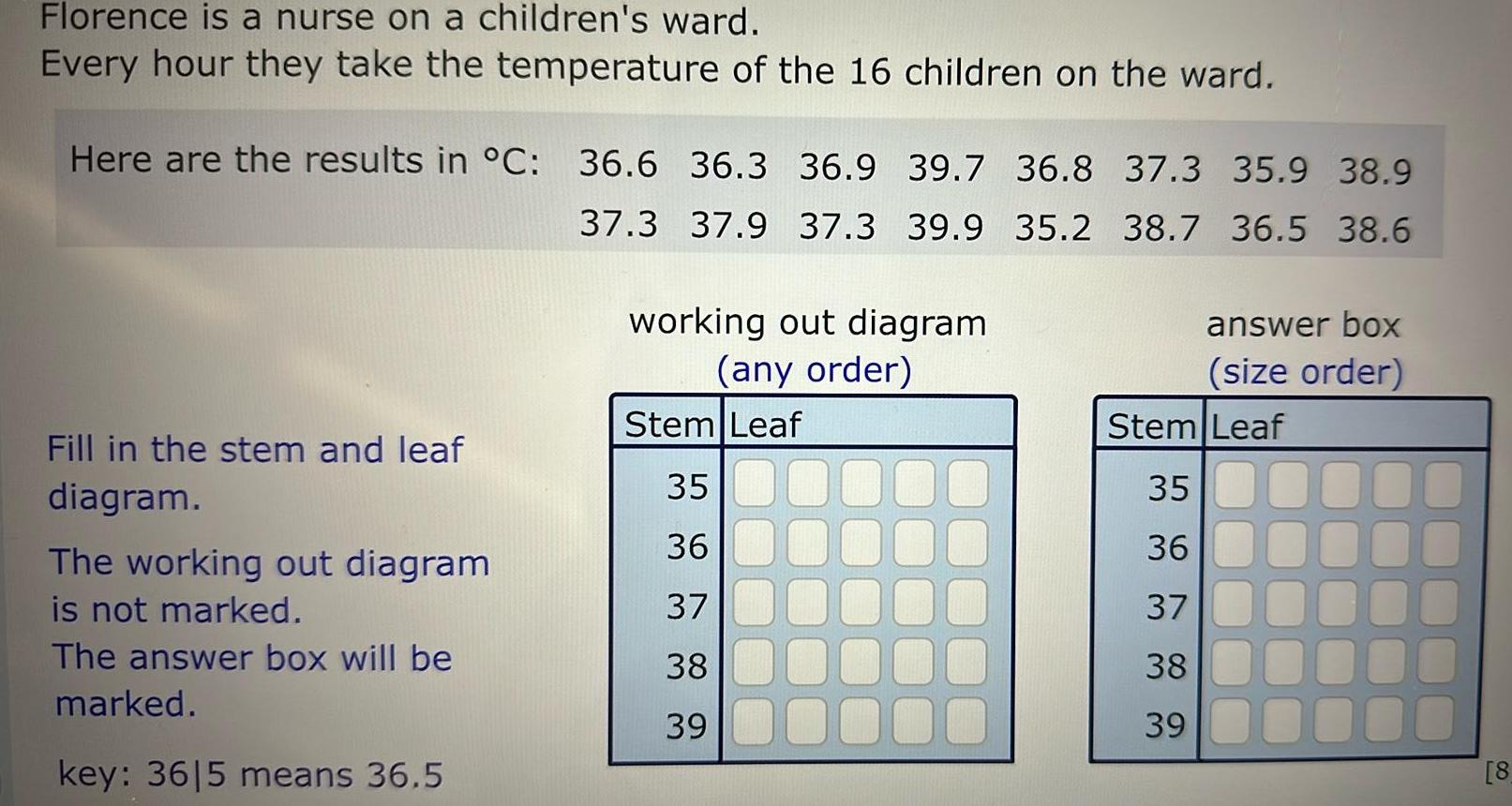
3D GeometryFlorence is a nurse on a children s ward Every hour they take the temperature of the 16 children on the ward Here are the results in C 36 6 36 3 36 9 39 7 36 8 37 3 35 9 38 9 37 3 37 9 37 3 39 9 35 2 38 7 36 5 38 6 Fill in the stem and leaf diagram The working out diagram is not marked The answer box will be marked key 3615 means 36 5 working out diagram any order Stem Leaf 35 36 37 38 39 answer box size order Stem Leaf 35 36 37 38 39 8
Geometry
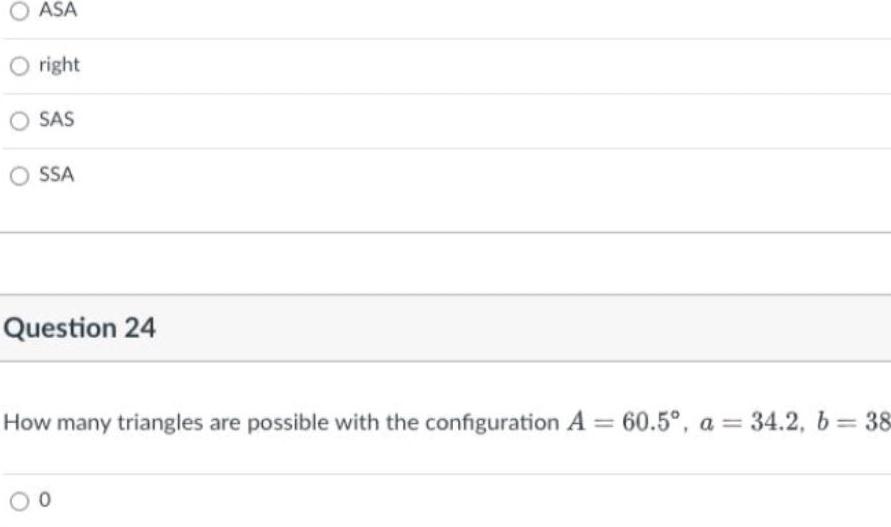
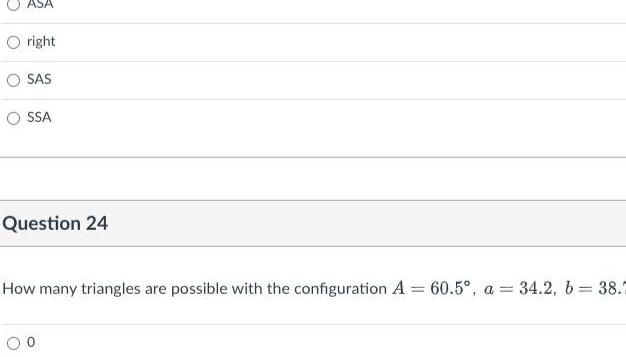
2D GeometryOASA right SAS SSA Question 24 How many triangles are possible with the configuration A 60 5 a 34 2 b 38 0
Geometry
Solution of trianglesOright SAS OSSA Question 24 How many triangles are possible with the configuration A 60 5 a 34 2 b 38 7

Geometry
2D GeometryTry This Match the function to the correct list of transformations One is done for you Function B f x x 1 3 f x 3 x 2 1 f x 3 x 1 2 3 x 1 x 1 List of Transformations A Horizontal compression shift right shift up B Vertical reflection vertical compression shift down C Horizontal stretch shift down D Vertical reflection vertical stretch shift left shift up
Geometry
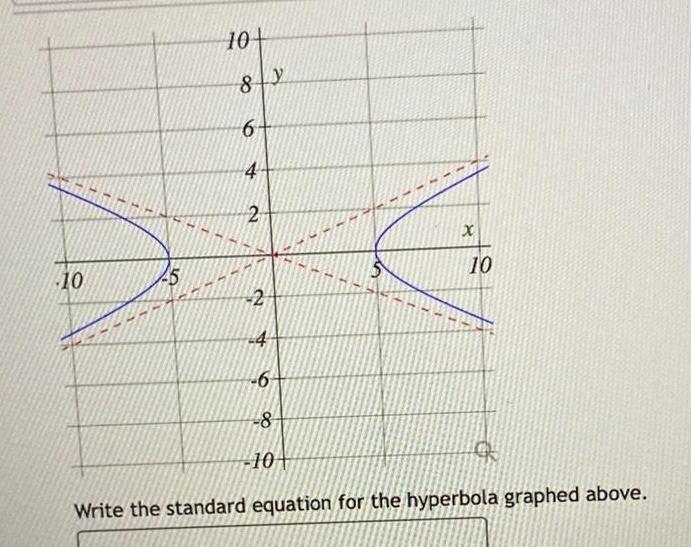
2D Geometry10 45 10 8Y 6 4 2 2 4 6 8 10 M 2 es t 7 x 10 Q Write the standard equation for the hyperbola graphed above
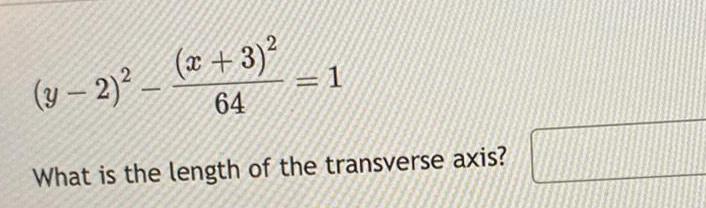
Geometry
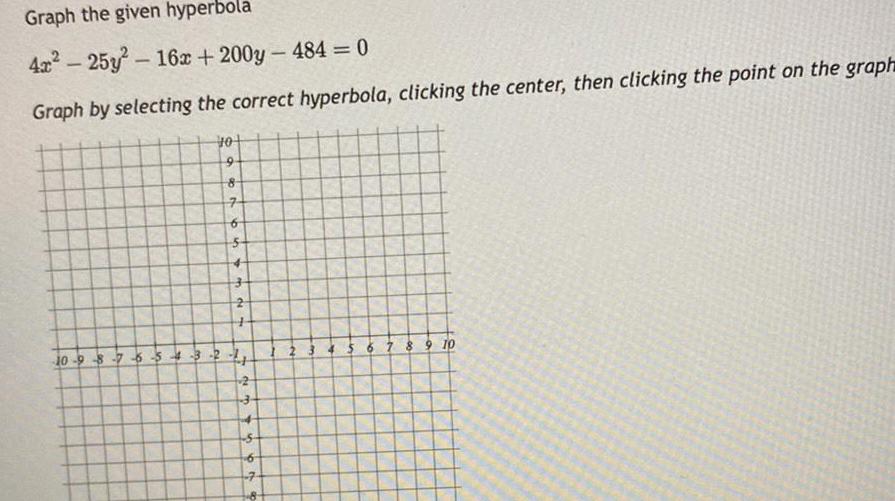
2D GeometryGraph the given hyperbola 4x 25y 16x 200y 484 0 Graph by selecting the correct hyperbola clicking the center then clicking the point on the graph 10 9 8 7 6 5 4 3 10 9 8 for 7 6 No 4 4 2 3 5676 5 8 9 10
Geometry
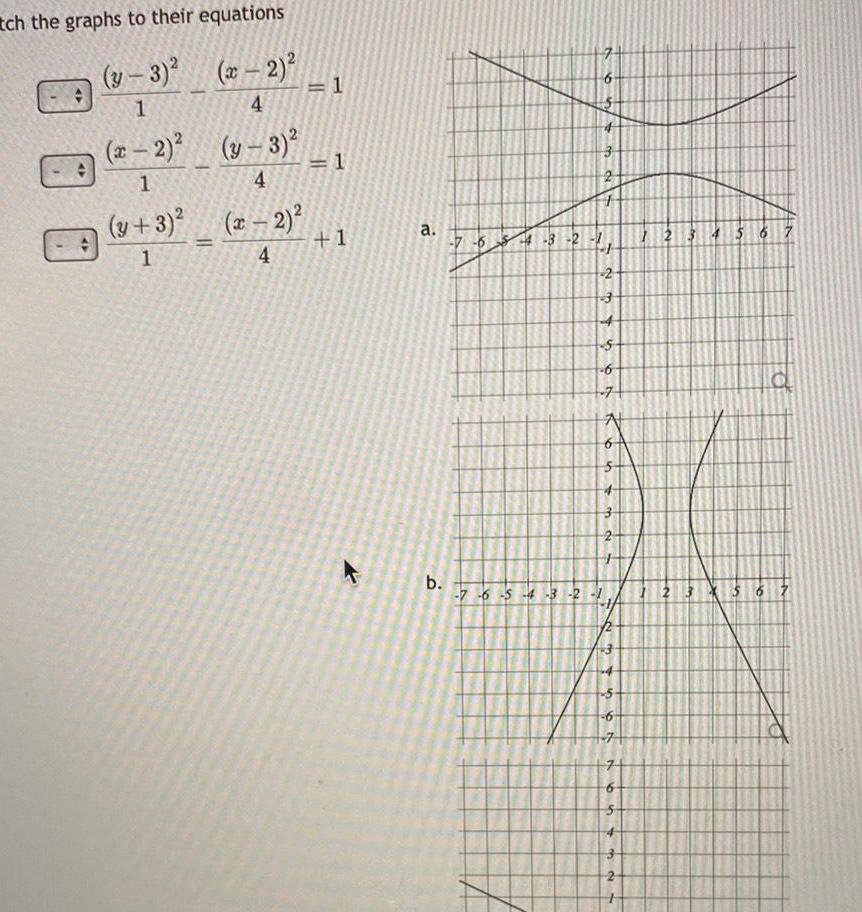
2D Geometrytch the graphs to their equations y 3 x 2 1 4 x 2 1 y 3 1 y 3 4 x 2 4 1 1 1 a b 7 7 654 3 2 1234 2 4 6 7 of 3 7 6 5 4 3 2 1 5 6 7 74 6 3 2 123 56 67
Geometry
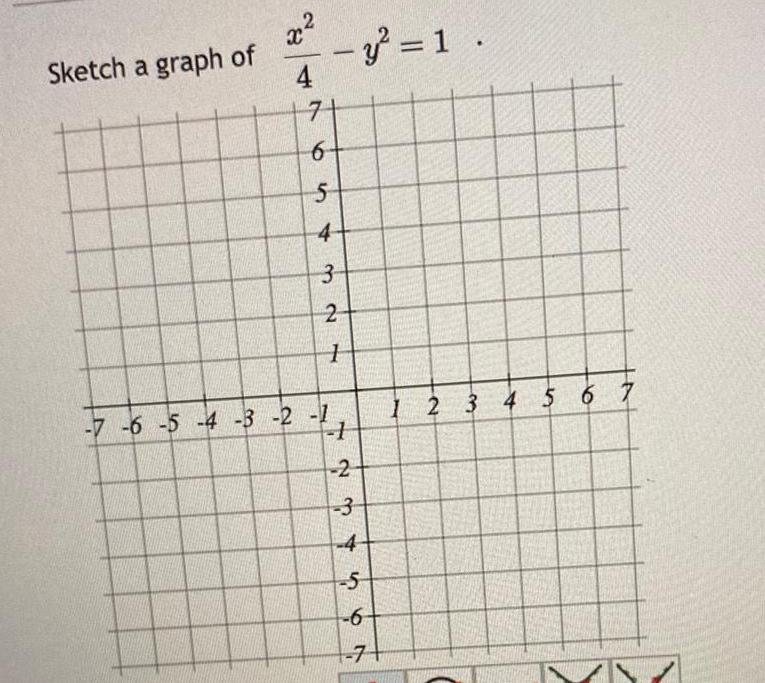
2D GeometrySketch a graph of x 4 y 1 71 65 6 4 32 3 7 7 6 5 4 3 2 1 1 2 3 4 5 6 1 71 1 2 3 4 5 6 7

Geometry
2D GeometryA swimming pool has the shape of a box with a base that measures 26 m by 19 m and a uniform depth of 2 9 m How much work is required to pump the water out of the pool when it 3 is full Use 1000 kg m for the density of water and 9 8 m s for the acceleration due to gravity Draw a y axis in the vertical direction parallel to gravity and choose one corner of the bottom of the pool as the origin For 0 sy 2 9 find the cross sectional area A y A y 494 Simplify your answer Set up the integral that gives the work required to pump the water out of the pool Use increasing limits of integration Select the correct choice below and fill in the answer boxes to complete your choice Type exact answers OA JO dy OB CHEER dx
Geometry
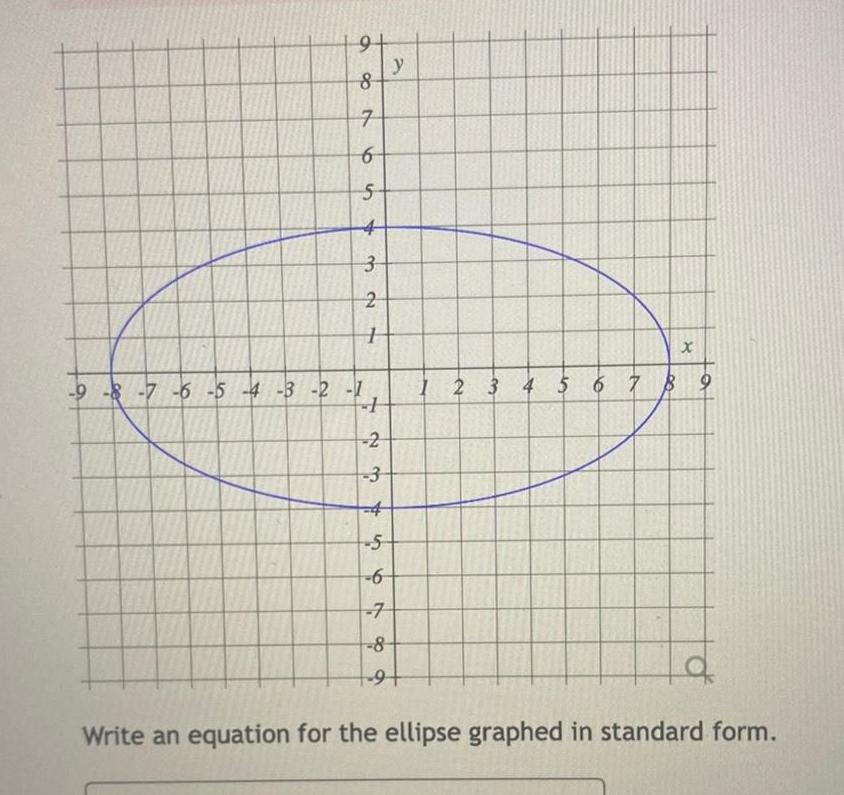
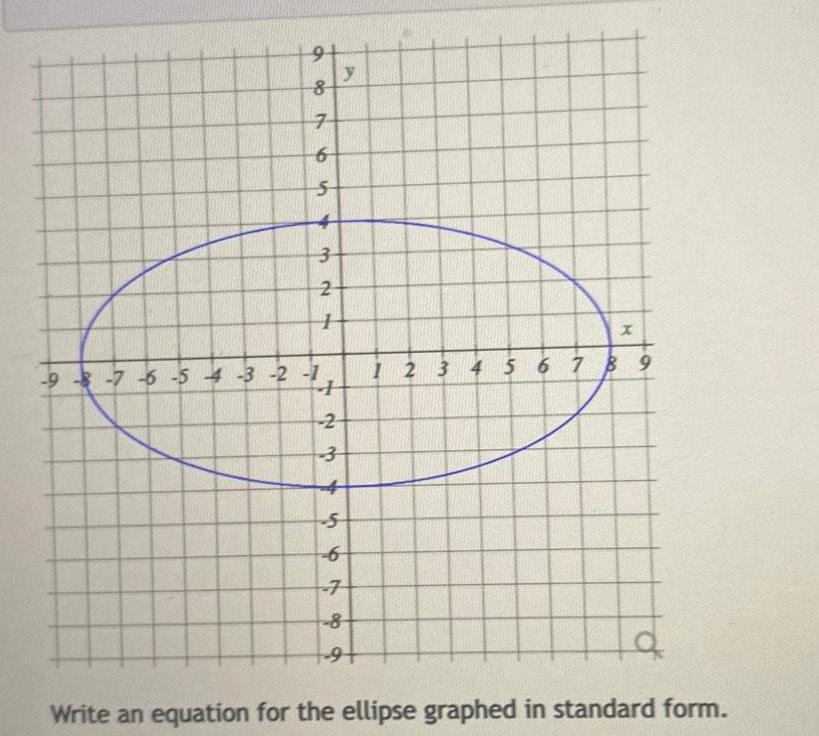
2D Geometry9 8 7 6 5 3 2 9 8 7 6 5 4 3 2 1 7 1 y 2 3 4 5 6 7 8 9 X 1 2 3 4 5 6 7 8 9 12 Write an equation for the ellipse graphed in standard form
Geometry
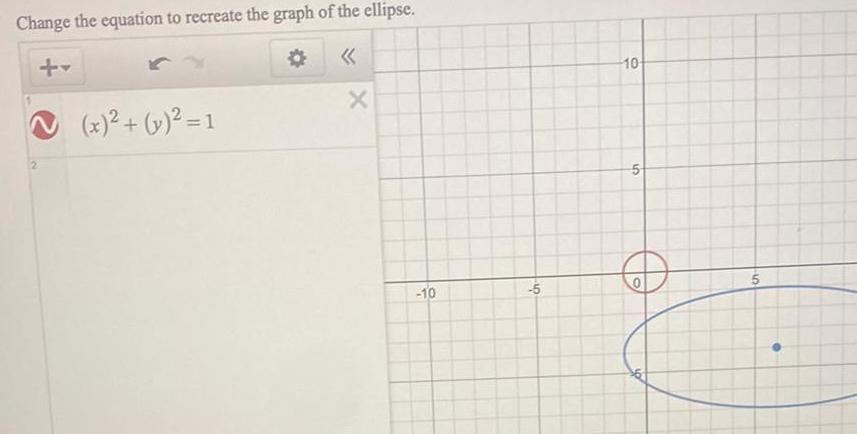
2D GeometryChange the equation to recreate the graph of the ellipse 2 x y 1 X 10 5 10 5 O 10
Geometry
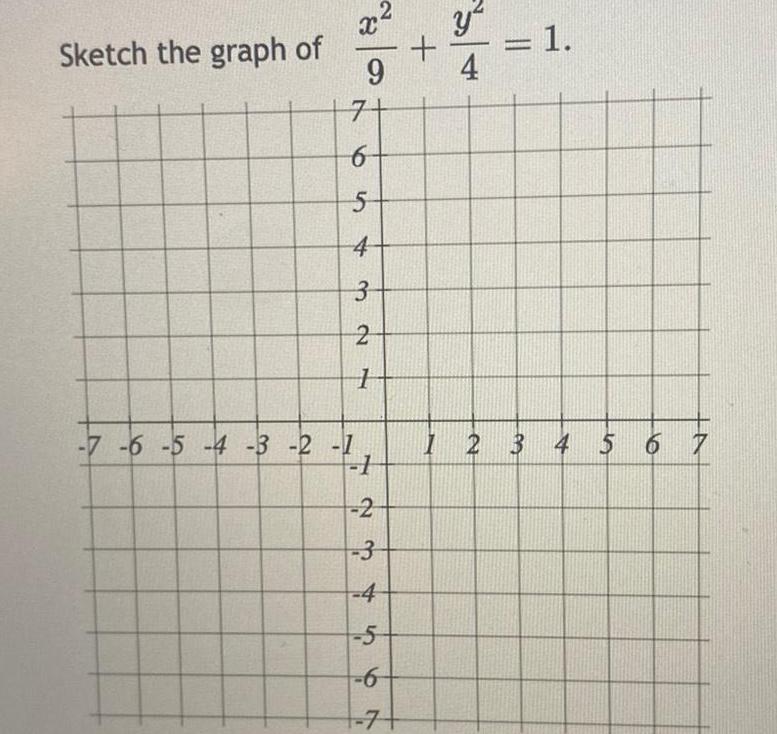
2D GeometrySketch the graph of X 9 7 6 5 4 3 2 7 2 7 6 5 4 3 2 1 1 2 3 4 5 6 y 4 1 1 2 3 2 3 4 5 6 7
Geometry
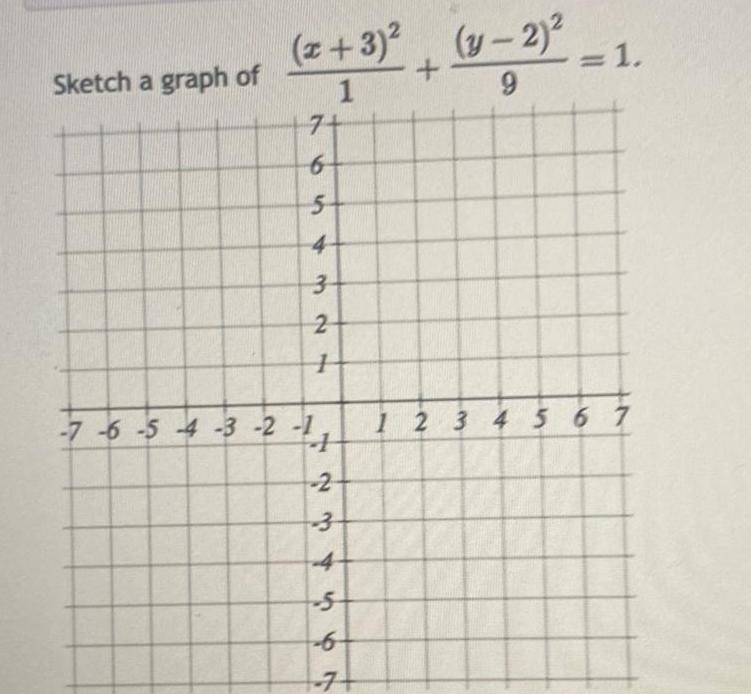
Coordinate systemSketch a graph of x 3 1 7 65324 5 7 6 5 4 3 2 1 1234 7 y 2 9 1 1 2 3 4 5 6 7
Geometry
2D Geometry91 y 8 6 ob 26 7 6 1 3 2 9 7 6 5 4 3 2 1 4 2 23 4 456 6 8 9 X 1 2 3 4 5 6 7 8 9 a Write an equation for the ellipse graphed in standard form

Geometry
Coordinate systeme m22 m26 What theorem can be used to prove that line a and line b are parallel Lesson 4 3 1 point A Converse of Alternate Exterior Angles OB Converse of Corresponding Angles DC Converse of Alternate Interior Angles OD Converse of Supplementary Angles 12 34 87 65
Geometry
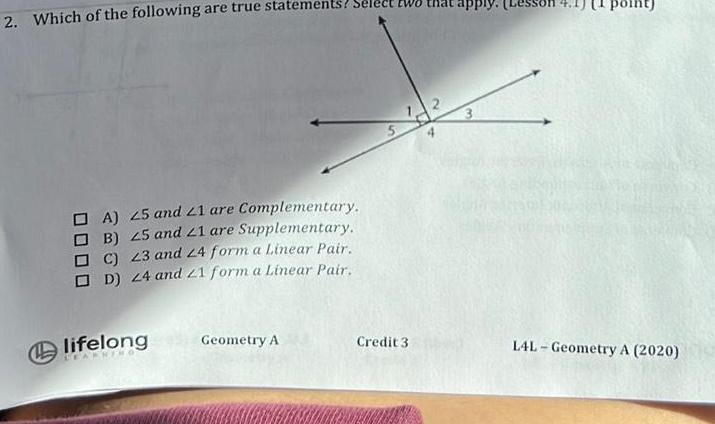
2D Geometry2 Which of the following are true statements Sele A 25 and 21 are Complementary B 25 and 21 are Supplementary C 23 and 24 form a Linear Pair D 24 and 21 form a Linear Pair lifelong LEAKNE Geometry A Credit 3 L4L Geometry A 2020
Geometry
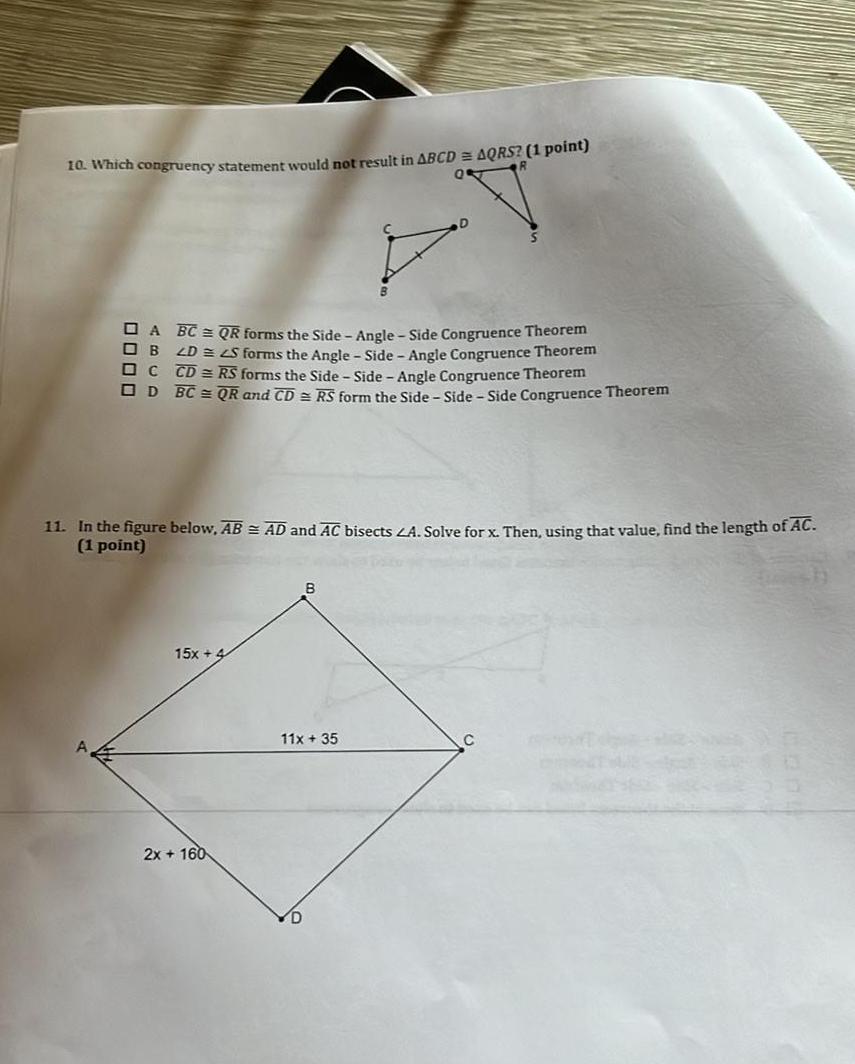
2D Geometry10 Which congruency statement would not result in ABCD AQRS 1 point A BC QR forms the Side Angle Side Congruence Theorem OB 2D S forms the Angle Side Angle Congruence Theorem C CD RS forms the Side Side Angle Congruence Theorem OD BC QR and CD RS form the Side Side Side Congruence Theorem 11 In the figure below AB AD and AC bisects A Solve for x Then using that value find the length of AC 1 point 15x 4 2x 160 B 11x 35 E 13

Geometry
3D GeometryESSMENT Practice Credit Checkpoint Complete the following Show all your work Road Construction The city of Interlaken has three amazing natural recreational areas a lake a cliff and a mountainous area Currently there are two businesses open in the area Half Moon Kayak Rentals and Chupacabra Campground Two new adventure companies want to open their businesses in this area to attract adventure seeking tourists However the issue is the only road that runs through this area is Lombard Road The city wants to build more roads to make the recreational areas accessible to tourists Construct the roads with a ruler and protractor to meet the city s criteria 2 points Interlaken s Road Criteria A straight road must begin at Chupacabra campground and end at iJump Adventure Company A straight road must begin at Half Moon Kayak Rentals and end at Surge Bike Excursions A straight road must pass by iJump Adventure Co and Surge Bike Excursions but never intersect Lombard Road Name the roads and provide appropriate angle measures of all intersecting roads for construction Chupacabra Campground Lombard Road Half Moon Kayak Rentals Surge Bike Excursions
Geometry
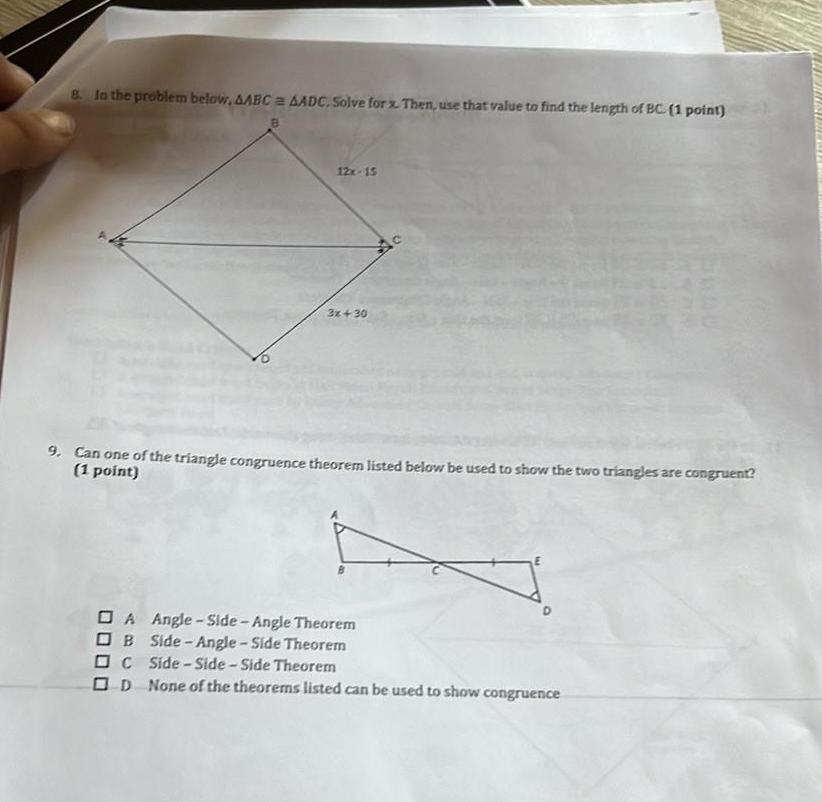
Heights & Distances8 In the problem below AABC AADC Solve for x Then use that value to find the length of BC 1 point B 12x 15 3x 30 BEAU 9 Can one of the triangle congruence theorem listed below be used to show the two triangles are congruent 1 point A Angle Side Angle Theorem OB Side Angle Side Theorem DC Side Side Side Theorem OD None of the theorems listed can be used to show congruence

Geometry
3D Geometry3 Answer the following for the given figure Lesson 4 2 1 point a Suppose 21 is 105 List all the angles congruent to21 Ejib 739 b Suppose 23 is also 105 Name all angles supplementary to 23 What is their measurement A Converse of Alternate Exterior Angles OB Converse of Corresponding Angles C Converse of Alternate Interior Angles D Converse of Supplementary Angles Liner and lines are parallel Answer the following about the given figure Lesson 4 2 1 point 103 c Which angle pairs are alternate interior angles List all angle pairs d What theorem explains why 24 28 e Which angle pairs are same side interior angles List all angle pairs 4 In the figure mz2 m26 What theorem can be used to prove that line a and line b are parallel Lesson 4 3 1 point 0 b 12 34 87 65

Geometry
3D GeometryLearning Goal from Lesson 5 1 5 4 I can show that triangles are congruent if and only if their corresponding sides and angles are congruent I can prove the following triangle congruence theorems ASA SAS SSS using properties of rigid motion A B How I Did Circle one 7 State the additional congruency statement s needed to prove AABC AFGH for the given theorem 1 point H I got it I m still learning it G a What is the missing side or angle needed to prove AABC AFGH using the SAS Theorem b What is the missing side or angle needed to prove AABC AFGH using the ASA Theorem
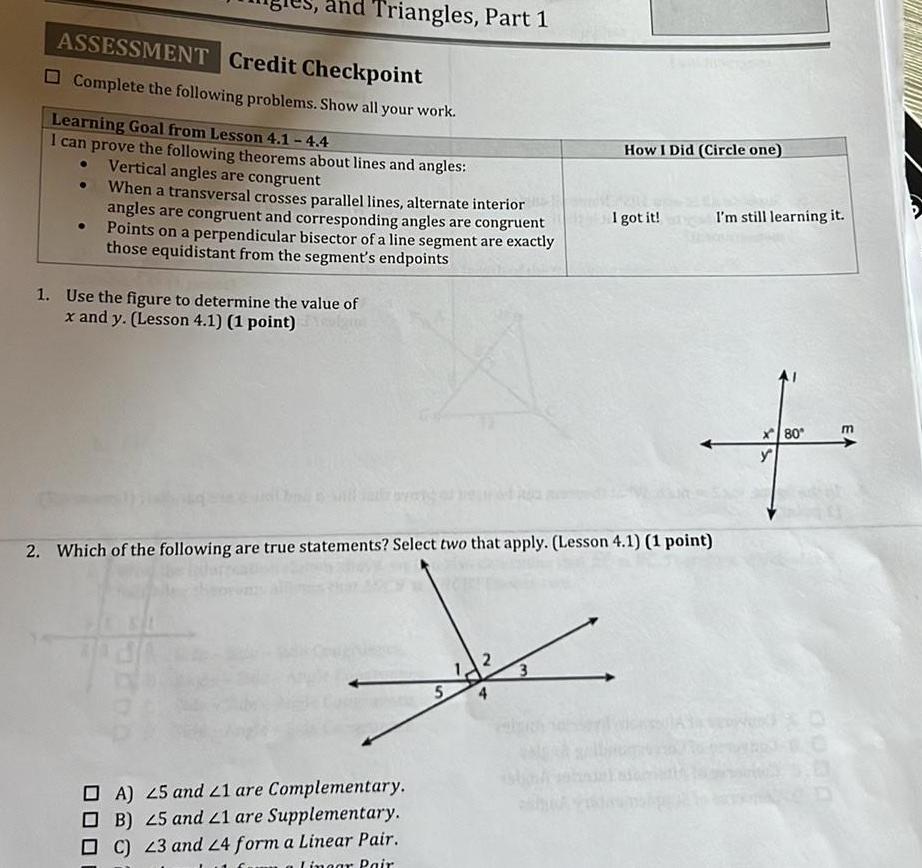
Geometry
Heights & DistancesASSESSMENT Credit Checkpoint Complete the following problems Show all your work Triangles Part 1 Learning Goal from Lesson 4 1 4 4 I can prove the following theorems about lines and angles Vertical angles are congruent When a transversal crosses parallel lines alternate interior angles are congruent and corresponding angles are congruent Points on a perpendicular bisector of a line segment are exactly those equidistant from the segment s endpoints 1 Use the figure to determine the value of x and y Lesson 4 1 1 point OA 25 and 21 are Complementary OB 25 and 21 are Supplementary C 23 and 24 form a Linear Pair Lingar Pair 5 2 Which of the following are true statements Select two that apply Lesson 4 1 1 point 2 3 How I Did Circle one ch I got it I m still learning it m x80

Geometry
Areathis figure mz1 135 Which of these statements is enough to prove that line m and line n are parallel Lesson 4 3 1 point A m2 45 B m23 135 C mz5 135 D m24 45 b CH 135 6 AC is the perpendicular bisector of GH Determine the length of the following sides Lesson 4 4 1 point a GH guter 100 m B X 8 12 A Side Side Side Congruence B Angle Side Angle Congruence C Side Side Angle Congruence OD Side Angle Side Congruence c With the information shown above we can also determine that BC BC Therefore which of the following theorems affirms that AGCB AHCB Choose two

Geometry
2D GeometryYour Turn 1 Determine whether A DEFA GHJ Justify your reasoning EXPLAIN 2 Proving Triangles Are Congruent Using SAS Triangle Congruence Read Explain 1 and complete Your Turn 1 2 adapted from Lesson 5 3 Show all your work Given CD bisects AE Prove A ABC A EBD The SAS Triangle Congruence Theorem may be used as a reason in a proof To complete the proof you need to show that two sides and the included angle of one triangle are congruent to the corresponding sides and angle of the other triangle Example Use the figure to the right to complete the two column proof and AE bisects CD Statements 1 CD bisects AE 2 AB EB 3 AB EB 4 AE bisects CD 5 CB DB E H 2 5 cm 2 5 cm 77 2 9 cm 6 CB DB 4 LABC LEBD 5 AABC A EBD DO 1 7 cm 4 Given Reasons 1 Given 2 Definition of a Bisector 3 Definition of Congruence 5 Definition of a Bisector 6 Definition of Congruence 4 Vertical Angles are Congruent 5 SAS Triangle Congruence Theorem G 1 7 cm
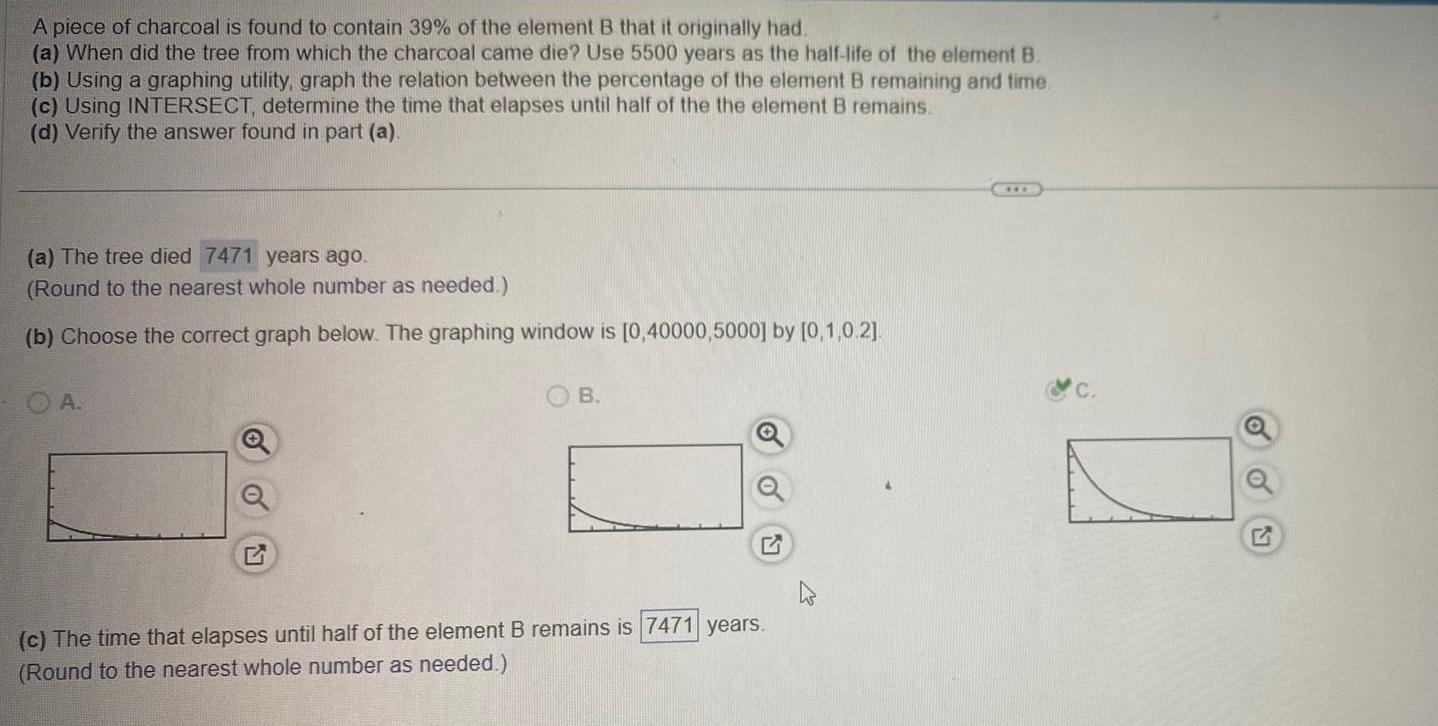
Geometry
Solution of trianglesA piece of charcoal is found to contain 39 of the element B that it originally had a When did the tree from which the charcoal came die Use 5500 years as the half life of the element B b Using a graphing utility graph the relation between the percentage of the element B remaining and time c Using INTERSECT determine the time that elapses until half of the the element B remains d Verify the answer found in part a a The tree died 7471 years ago Round to the nearest whole number as needed b Choose the correct graph below The graphing window is 0 40000 5000 by 0 1 0 2 A B c The time that elapses until half of the element B remains is 7471 years Round to the nearest whole number as needed Q

Geometry
2D GeometryHW 1 What additional information would be enough to prove that the two triangles are congruent by SAS L Homework Complete problems 1 6 below for independent practice A HG ZX B TG 2X C LG LX D 2H ZY HHH H When you are finished check the solutions with your teacher A XHXY OBJH WY C ZW D 2N ZY 3 Determine if the triangles below are congruent If 4 Determine if the triangles below are congruent If so what properties are used in your logic so what properties are used in your logic M 5 State what additional information is required to prove AUML AKLM by SAS 2 What additional information would be enough to prove that the two triangles are congruent by SAS 6 State what additional information is required to prove AJHI AUSI by SAS Optional Complete problems 1 3 4 6 7 11 12 14 from your textbook on separate lined paper When you are finished check the odd problems for solutions at the back of the textbook

Geometry
2D Geometry1 Find the values for x that results in A FGH A TUV 2 Find the values for y that results in A FGH A TUV 7y 4 T G 60 30 C 8x 12 cm 12 cm H


Geometry
2D GeometryHW 5 4 Homework 1 What additional information is needed to prove that the two triangles are congruent by SSS Complete problems 1 6 below for independent practice A HG VT BHFVT C LG LV D LF LT S G U tice When you are finished check the solutions with your teacher H 2 What additional information is needed to prove that the two triangles are congruent by SSS N 3 Determine if the triangles below are congruent 4 Determine if the triangles below are congruent If so what properties are used in your logic If so what properties are used in your logic 5 State what additional information is required to 6 State what additional information is required to prove AUMLAKLM by SSS prove AYGE AFGE by SSS M Y H F M ASN MN B LN LN CLM LS D LLNS ZLNM E Optional Complete problems 11 15 23 from your textbook on separate lined paner
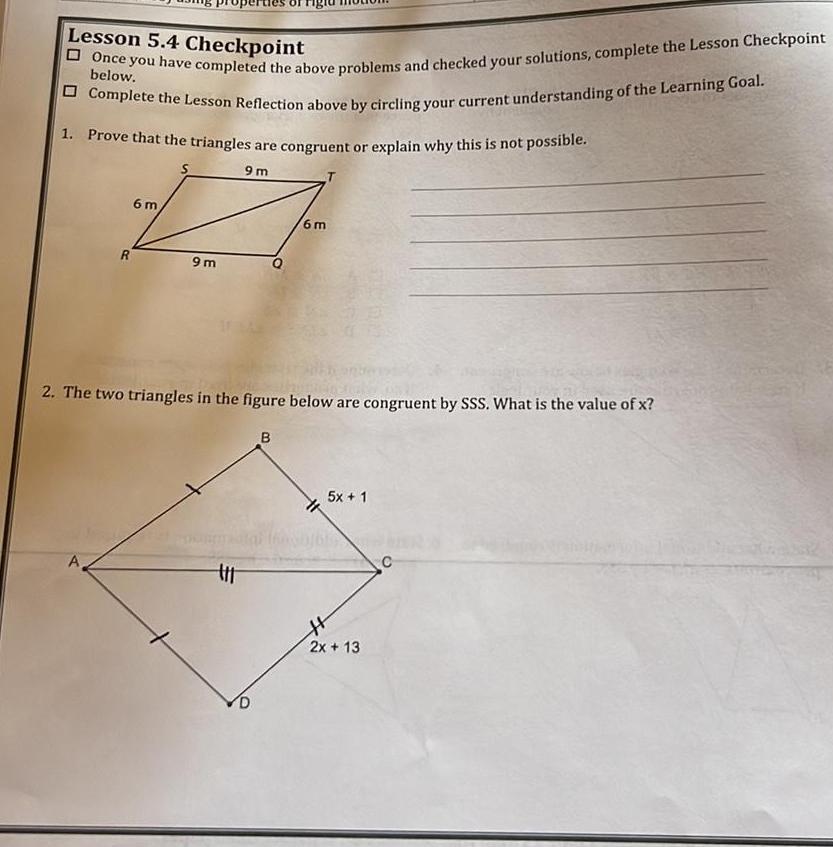
Geometry
VectorsLesson 5 4 Checkpoint below Once you have completed the above problems and checked your solutions complete the Lesson Checkpoint Complete the Lesson Reflection above by circling your current understanding of the Learning Goal 1 Prove that the triangles are congruent or explain why this is not possible 9m R A 6 m 9m 2 The two triangles in the figure below are congruent by SSS What is the value of x t D 6m B 5x 1 H 2x 13 C

Geometry
2D GeometryDetermine whether the triangles are congruent Explain your reasoning congrene papan you A 45 2 3 cm 61 C D 2 3 cm

Geometry
Coordinate systemties of rigid motion Starting b Rob says that AB AC and BD CD Do you agree Explain Getting there Lesson 5 2 Checkpoint Once you have completed the above problems and checked your solutions complete the Lesson Checkpoint Complete the Lesson Reflection above by circling your current understanding of the Learning Goal 1 Rob is making the kite shown in the figure a Can Rob conclude that AABD AACD Why or why not A Got it
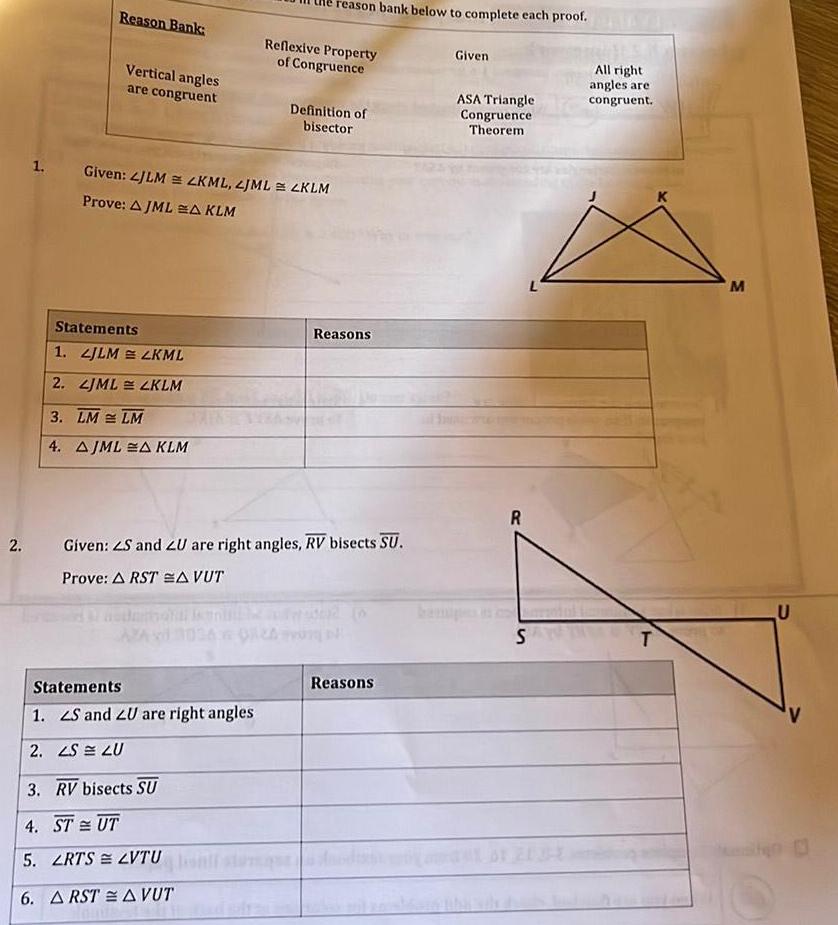
Geometry
2D GeometryReason Bank Vertical angles are congruent Statements 1 JLM LKML 2 LJML LKLM 3 LM LM 4 AJMLA KLM 1 Given LJLM LKML LJML LKLM Prove AJMLA KLM AZAS reason bank below to complete each proof Reflexive Property of Congruence Statements 1 S and ZU are right angles 2 LS LU 3 RV bisects SU 4 STUT 5 LRTS LVTU 6 ARSTA VUT Definition of bisector 2 Given ZS and LU are right angles RV bisects SU Prove ARSTA VUT Reasons Reasons Given ASA Triangle Congruence Theorem R S All right angles are congruent T M U

Geometry
Solution of trianglesetermine whether A MNPA QRS Justify your reasoning R 38 in 54 in 47 38 in N S M 32 in 28 in 54 in Q

Geometry
3D Geometry2 1 Your Turn E Reason Bank Choose from the phrases in the reason bank below to complete each proof Vertical angles are congruent Given AB AD and 21 22 Prove A BACA DAC Statements 1 AB AD 2 41 42 3 AC AC 4 A BACA DAC 2 AC CD 2 EC CB 3 AC CD 3 EC CB Given C is the midpoint of AD and BE Prove A ABC A DEC Statements 1 C is the midpoint of AD and BE Reflexive Property of Congruence 5 LACB LDCE ARCA DEC Definition of Bisector Reasons Reasons Given SAS Triangle Congruence Theorem Definition of Congruence B B 4

Geometry
Solution of trianglesEVALUATE Lesson 5 2 Homework HW Complete problems 1 6 for independent practice 1 What additional information would be enough to prove the triangles are congruent by ASA T D A VT UY OBVY TU When you are finished check the solutions with your teacher C ZTVU ZYUV OD 2T LY 3 Determine if the triangles below are congruent If so what properties are used in your logic 5 State what additional information is required to prove AZXY APRY by ASA R 2 What is the value of b in the following diagram What property did you use to find it 74 4 State what additional information is required to prove AXYZ AJKL K Z L 6 State what additional information is required to prove ASRQ ACQR by ASA R Q Optional Complete problems 3 8 15 16 20 from your textbook on separate lined paper When you are finished check the odd problems for solutions at the back of the textbook
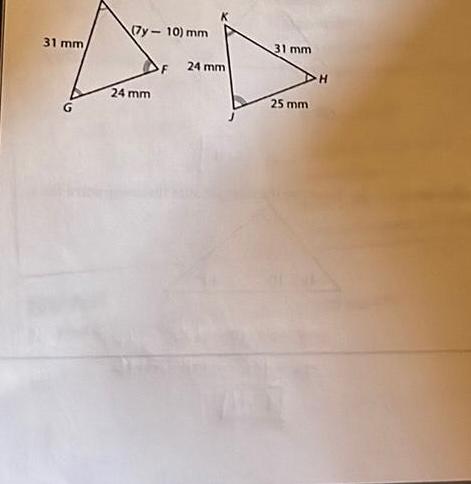

Geometry
Solution of triangles2 1 7 9 cm 1m M 60 30 A V 2m 1 7 m 1 7 m 2m 30 60 1 m 12 1 cm 8 5 cm B E 8 4 cm 12 1 cm 7 9 cm 2H2L 2 2M GH KL HJ LM GJ KM Because all of the corresponding parts of the triangles are congruent A GHJA KLM LG 4K Here we are only given the sides of the triangles AB DE AC DF But BC is not congruent to EF Therefore the triangles are not congruent

Geometry
2D Geometrythose equidistant from the segment s endpoints ular bisector of a line segment are out lines and angles T T Lesson 4 4 Checkpoint Once you have completed the above problems and checked your solutions complete the Lesson Checkpoint below Complete the Lesson Reflection above by circling your current understanding of the Learning Goal 1 If QR 12 and QR is a perpendicular bisector of TS determine which of the following claims are true 6x 4 RS 12 x 4 x 3 RS 5 RS 4 ST 10 QR 4 QT 16 2x 1 True Q90 True True True True True True True R R Q90 3x 8 False 2 If QS 4 and QR is a perpendicular bisector of TS determine which of the following claims are true False False False 4x 3 Starting False False False False Getting there S S Got it
Geometry
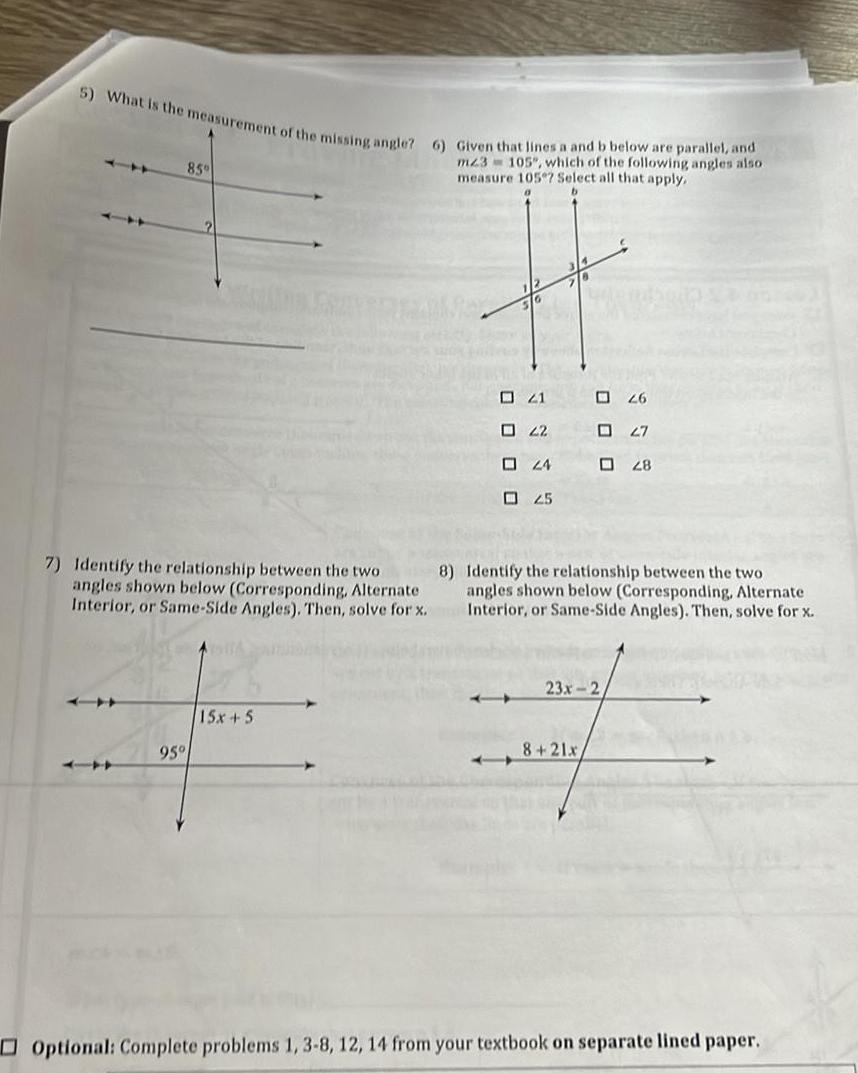
Coordinate system5 What is the measurement of the missing angle 6 Given that lines a and b below are parallel and m23 105 which of the following angles also measure 105 Select all that apply 85 95 16 15x 5 21 22 24 02 5 0 0 0 8 7 Identify the relationship between the two angles shown below Corresponding Alternate Interior or Same Side Angles Then solve for x Identify the relationship between the two angles shown below Corresponding Alternate Interior or Same Side Angles Then solve for x 8 21x 26 02 7 23x 2 28 Optional Complete problems 1 3 8 12 14 from your textbook on separate lined paper

Geometry
2D Geometryour Turn Tell whether lines m and n must be parallel from the given information If they are state your reasoning 1 45 27 1 8 2 7 3 6 4 5 m

Geometry
AreaYour Turn Givens CE is the perpendicular bisector of FG Find the following lengths 1 Pind PD 2 Find CG 3 Find PG 8 E

Geometry
Solution of trianglesHW e 1 Which side of VXS side matches SQ AQRS AVXS SQ 65 R 7x 12 Homework Complete problems 1 4 below for independent practice S 3 Based on the triangle sum theorem solve for x When you are finished check the solutions with your teacher 40 ce When you are finished check the odd pro 2 Which angle on UHI matches W AVWU AUHI AA U ZW W 4 Based on the triangle sum theorem solve for x A 4x 10 Optional Complete problems 3 5 7 9 15 18 from your textbook on separate lined paper 40 Juni
Geometry
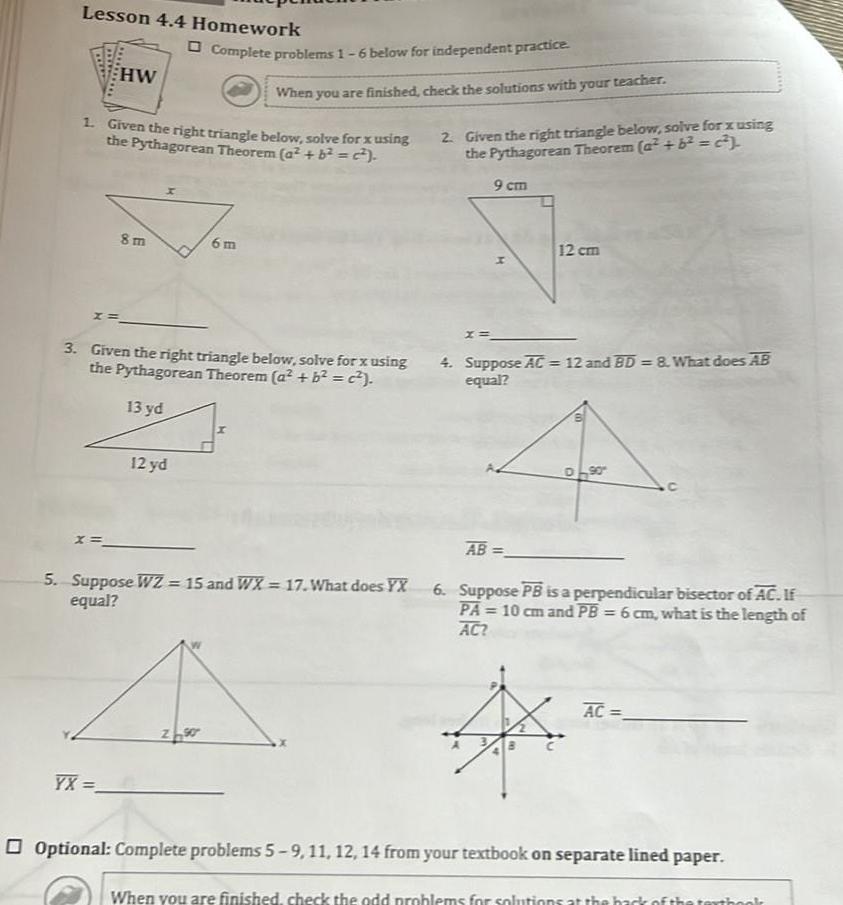
2D GeometryLesson 4 4 Homework x HW 1 Given the right triangle below solve for x using the Pythagorean Theorem a b c 8m YX Complete problems 1 6 below for independent practice 12 yd 3 Given the right triangle below solve for x using the Pythagorean Theorem a b 13 yd When you are finished check the solutions with your teacher 6m ZS 5 Suppose WZ 15 and WX 17 What does YX equal 2 Given the right triangle below solve for x using the Pythagorean Theorem a 6 2 9 cm 12 cm 4 Suppose AC 12 and BD 8 What does AB equal AB 90 6 Suppose PB is a perpendicular bisector of AC If PA 10 cm and PB 6 cm what is the length of AC AC Optional Complete problems 5 9 11 12 14 from your textbook on separate lined paper When you are finished check the odd problems for solutions at th

Geometry
2D GeometryLesson 4 3 Homework HW X x 1 Find the value of x that makes u v parallel X 26r 5 Complete problems 1 6 below for independent practice 2 Find the value of x that makes u v parallel 125 130 Independent Practice 6r 3 6r 4 45 3 Find the value of x that makes u v parallel 7x 1 When you are finished check the solutions with your teacher 17x 11 N 4 Find the value of x that makes us v parallel

Geometry
2D GeometryYour Turn 1 2 R 71 719 T Determine whether the given triangles are congruent Explain 38 D 700 S 38 U 71 71 W

Geometry
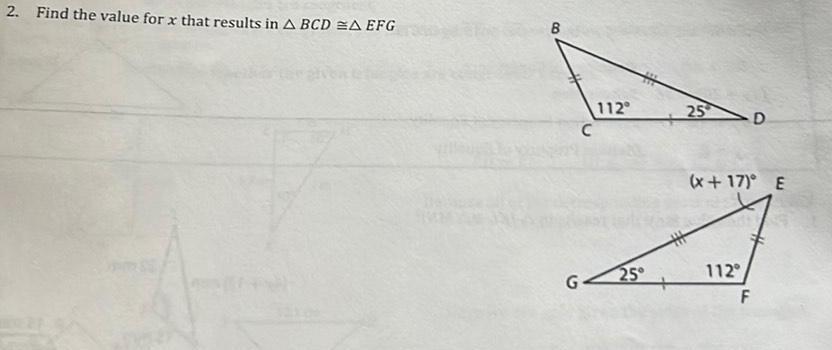
2D GeometryYour Turn If AD is 10 inches long BD is 6 inches long 1 Find the length of AB lifelong Geometry A Credit 3 A D B L4L Geometry A 2020 Page