Geometry Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
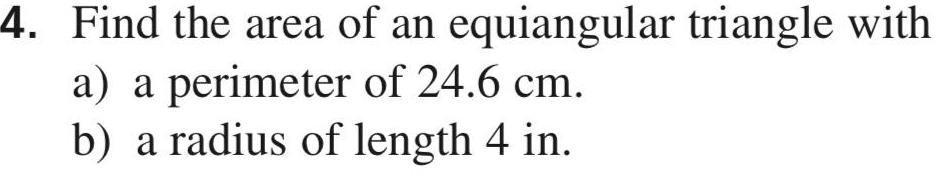
Geometry
3D Geometry4 Find the area of an a a perimeter of 24 6 cm b a radius of length 4 in equiangular triangle with

Geometry
2D GeometryIn Exercises 17 to 30 use the formula A area of the regular polygon described ap to find the 20 Find the area of a regular octagon with an anthem of length
Geometry
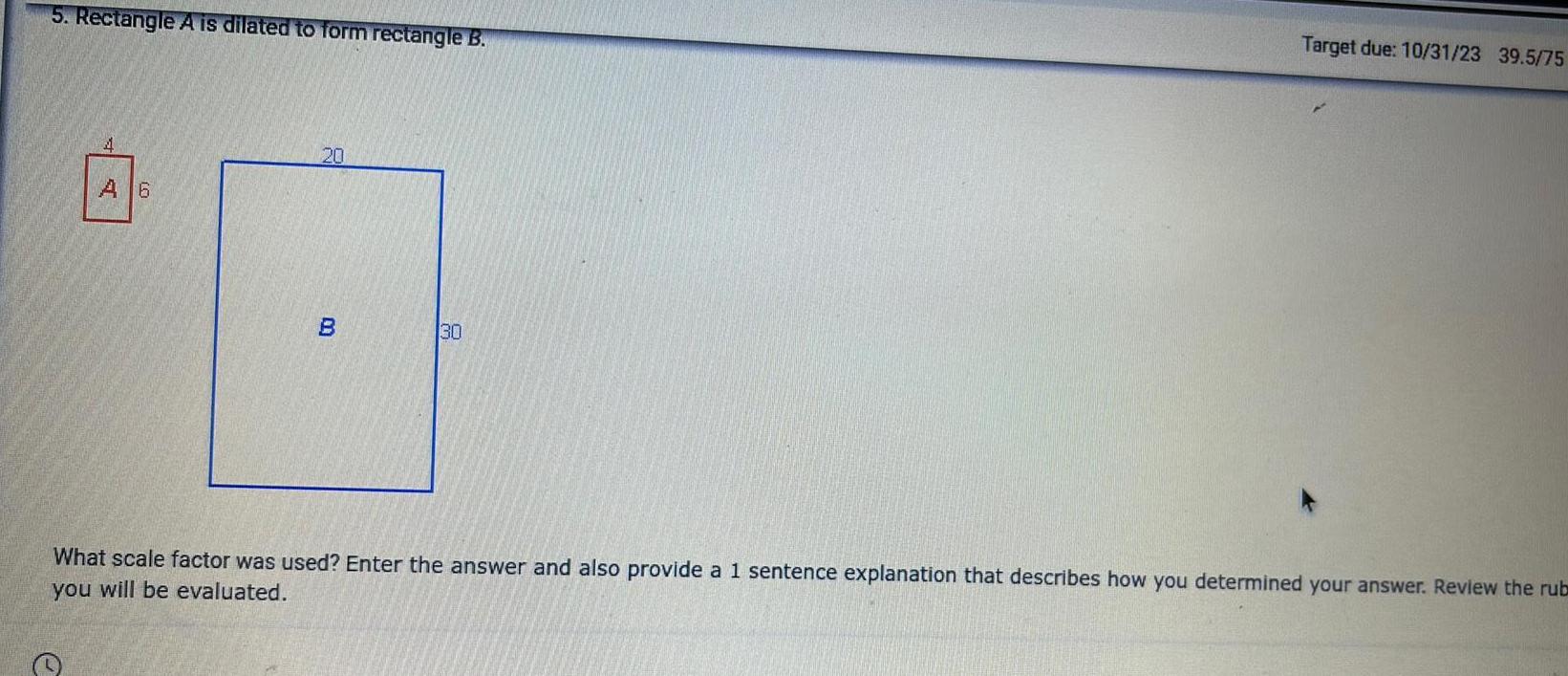
Heights & Distances5 Rectangle A is dilated to form rectangle B A 6 e 20 B 30 Target due 10 31 23 39 5 75 What scale factor was used Enter the answer and also provide a 1 sentence explanation that describes how you determined your answer Review the rub you will be evaluated

Geometry
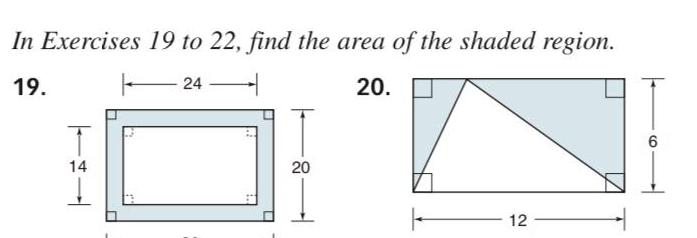
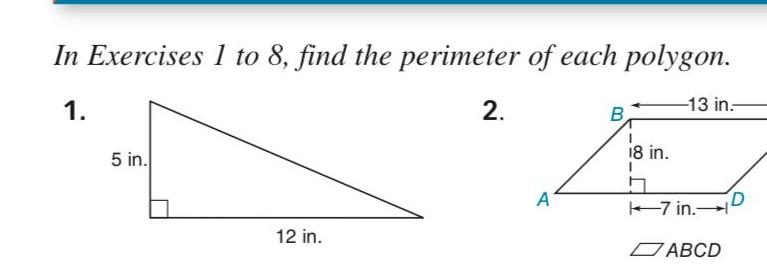
AreaIn Exercises 1 to 8 find the perimeter of each polygon 13 in 1 5 in 12 in 2 A B 18 in 7 in ABCD D
Geometry
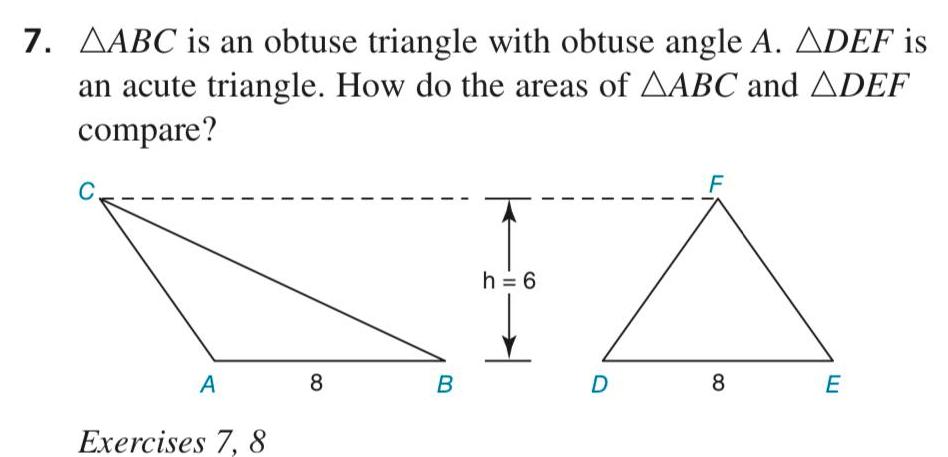
2D Geometry7 AABC is an obtuse triangle with obtuse angle A ADEF is an acute triangle How do the areas of AABC and ADEF compare A Exercises 7 8 8 B h 6 D 8 E
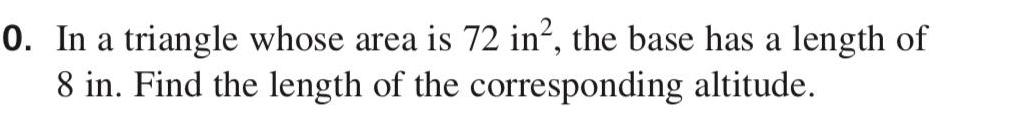
Geometry
2D Geometry0 In a triangle whose area is 72 in the base has a length of 8 in Find the length of the corresponding altitude
Geometry
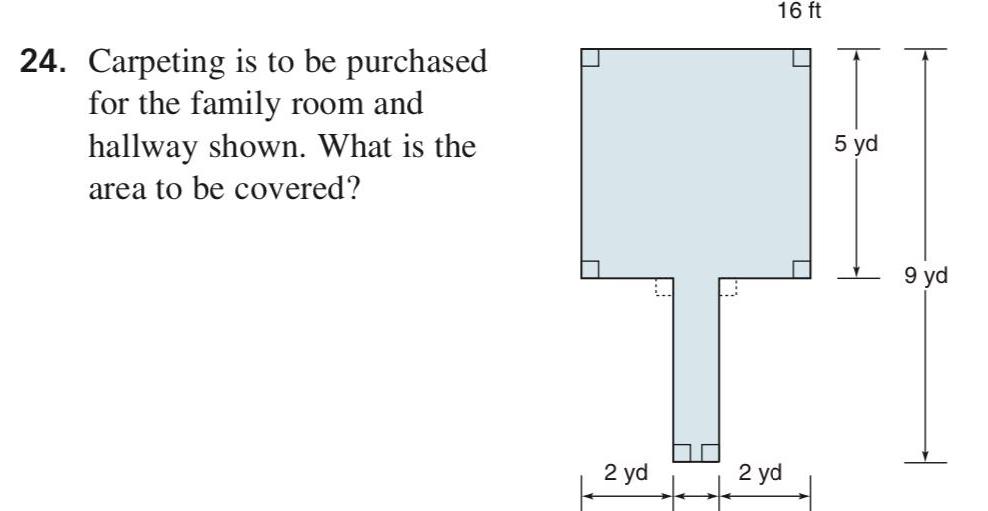
Area24 Carpeting is to be purchased for the family room and hallway shown What is the area to be covered 2 yd 16 ft 2 yd 5 yd 9 yd

Geometry
2D GeometryIn Exercises 9 to 18 find the areas of the figures shown or described 9 A rectangle s length is 6 cm and its width is 9 cm

Geometry
2D Geometry23 A triangular corner of a store has been roped off to be used as an area for displaying Christmas ornaments Find the area of the display section 24 ft

Geometry
Coordinate systemIn Exercises 20 and 21 use Theorem 9 2 1 in which the lengths of apothem a altitude h and slant height of a regular pyramid are related by the equation 2 a h 20 In a regular square pyramid whose base edges measure 8 in the apothem of the base measures 4 in If the height of the pyramid is 8 in find the length of its slant height

Geometry
3D Geometry13 Assume that the number of sides in the base of a pyramid is n Generalize the results found in earlier exercises by answering each of the following questions a What is the number of vertices b What is the number of lateral edges c What is the number of base edges d What is the total number of edges e What is the number of lateral faces f What is the total number of faces Note Lateral faces and base faces
Geometry
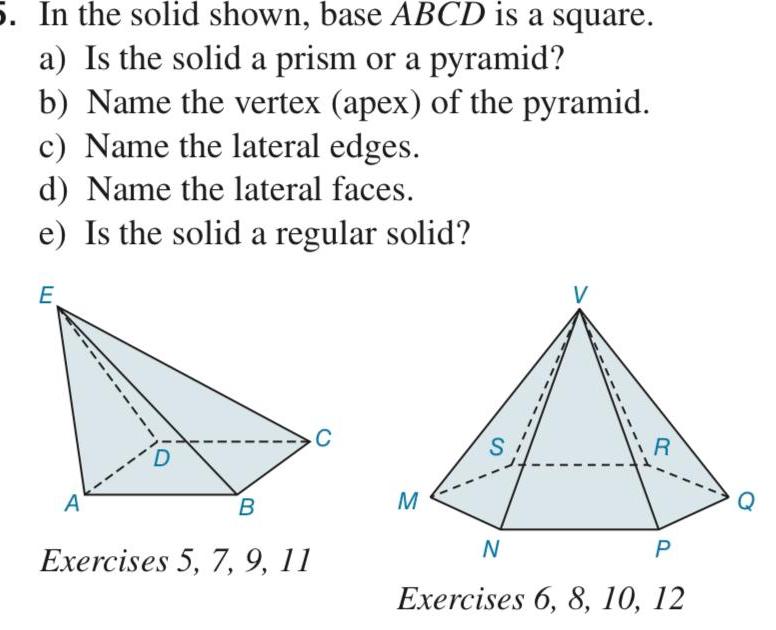
3D Geometry5 In the solid shown base ABCD is a square a Is the solid a prism or a pyramid b Name the vertex apex of the pyramid c Name the lateral edges d Name the lateral faces e Is the solid a regular solid E A B Exercises 5 7 9 11 C M S V N R P Exercises 6 8 10 12
Geometry
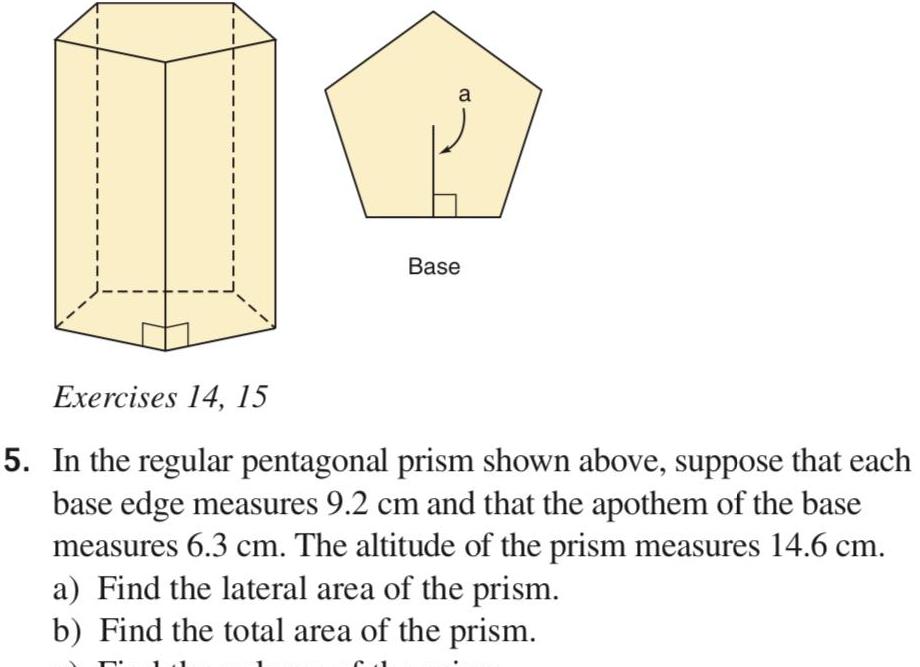
3D Geometrya Base Exercises 14 15 5 In the regular pentagonal prism shown above suppose that each base edge measures 9 2 cm and that the apothem of the base measures 6 3 cm The altitude of the prism measures 14 6 cm a Find the lateral area of the prism b Find the total area of the prism

Geometry
3D Geometry17 For the right triangular prism found in Exercises 16 17 Exercise 16 suppose that the sides of the triangular base measure 3 ft 4 ft and 5 ft The altitude is 6 ft in length a Find the lateral area of the prism b Find the total area of the prism c Find the volume of the prism

Geometry
Coordinate systemExercises 1 3 5 7 9 7 Suppose that each of the bases of the hexagonal prism in Exercise 1 has an area of 12 cm and that each lateral face h

Geometry
2D Geometrycentimeters in I cubic meter 19 Given that 12 in 1 cubic foot 1 ft find the number of cubic inches in
Geometry
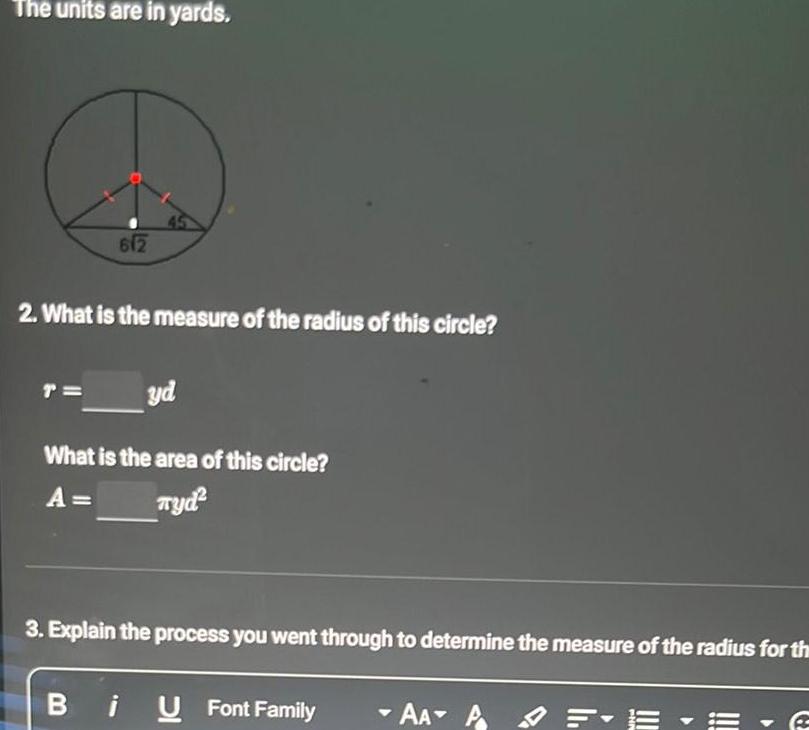
2D GeometryThe units are in yards 612 2 What is the measure of the radius of this circle T yd What is the area of this circle A Tyd 3 Explain the process you went through to determine the measure of the radius for the BiU U Font Family AA A PHN F


Geometry
Area5 O 10 What is the measure of the radius of the SMALL circle T Small Circle What is the area of the SMALL circle Asmall Circle ft ft What is the measure of the radius of the LARGE circle Large Circle ft What is the area of the LARGE circle ALarge Circle What is the EXACT area of the shaded region Am f42
Geometry
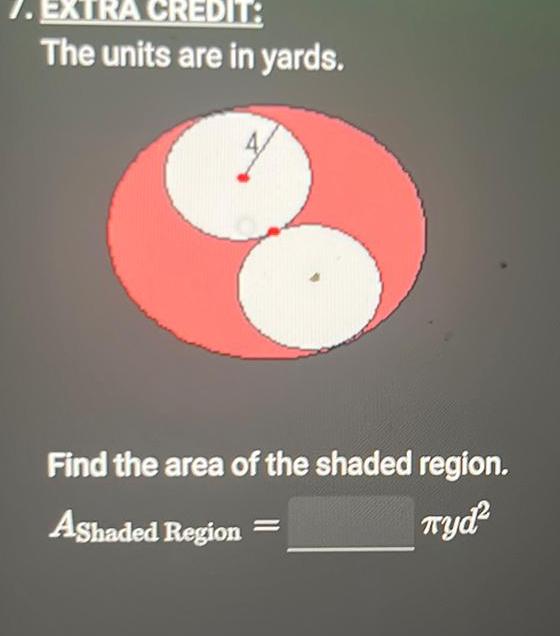
Heights & DistancesEXTRA CREDIT The units are in yards Find the area of the shaded region Ashaded Region Tyd
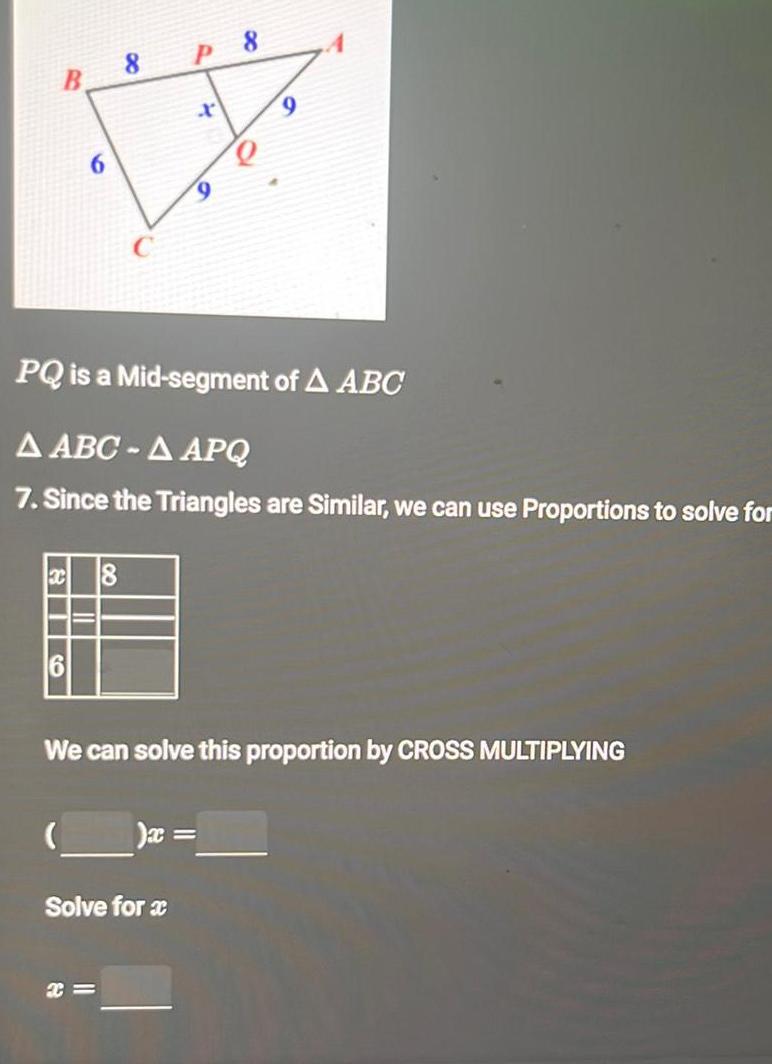
Geometry
2D GeometryB X 18 8 P X Solve for x x 9 PQ is a Mid segment of A ABC A ABC A APQ 7 Since the Triangles are Similar we can use Proportions to solve for x 8 We can solve this proportion by CROSS MULTIPLYING 9

Geometry
2D Geometry10 What is the measure of the radius of this circle mm What is the area of this circle Acircle TMM What is the area of the square mm Asquare What is the EXACT area of the shaded region Ashaded Region mm

Geometry
2D GeometryREDIT The units are in yards Find the area of the shaded region Ashaded Region Tkm
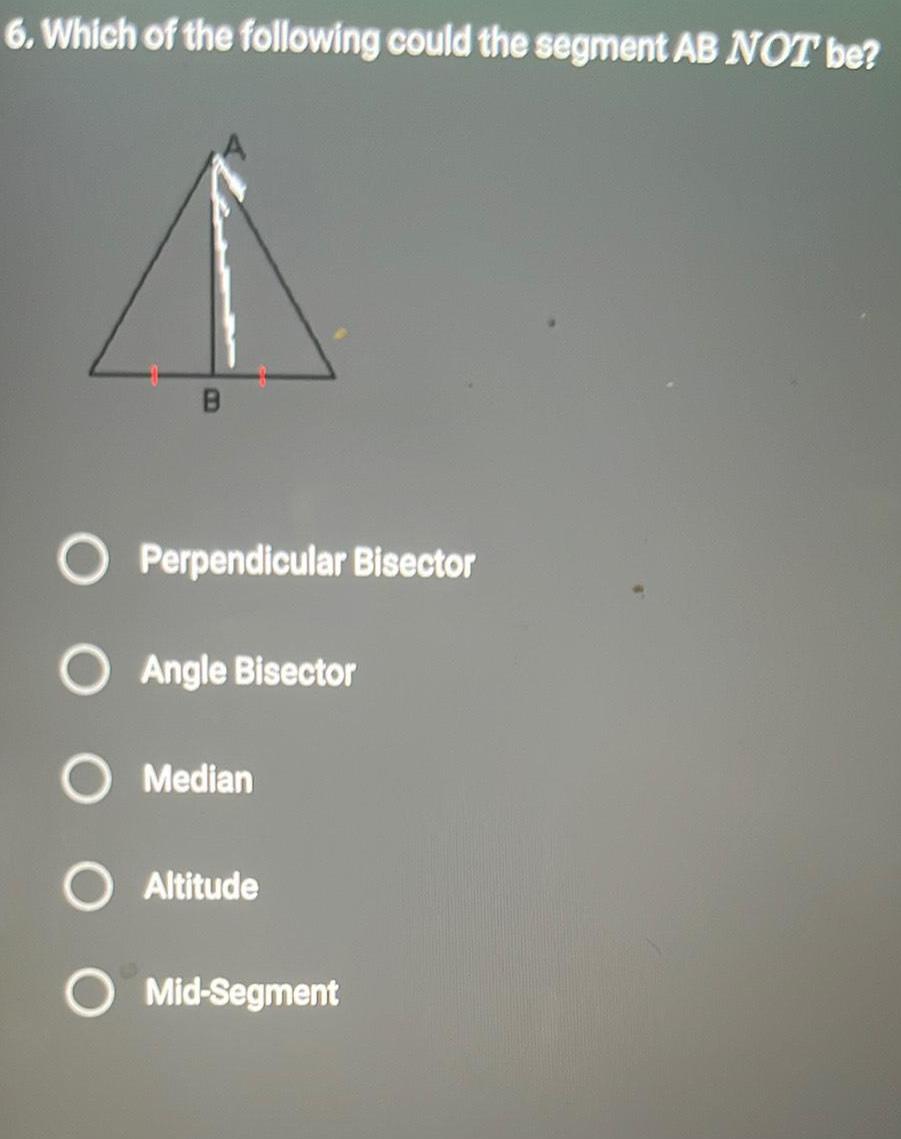
Geometry
Coordinate system6 Which of the following could the segment AB NOT be B O Perpendicular Bisector O Angle Bisector O Median Altitude Mid Segment

Geometry
2D Geometry1 The units are in miles 10 What is the measure of the radius of this circle T mi What is the area of this circle A TMi
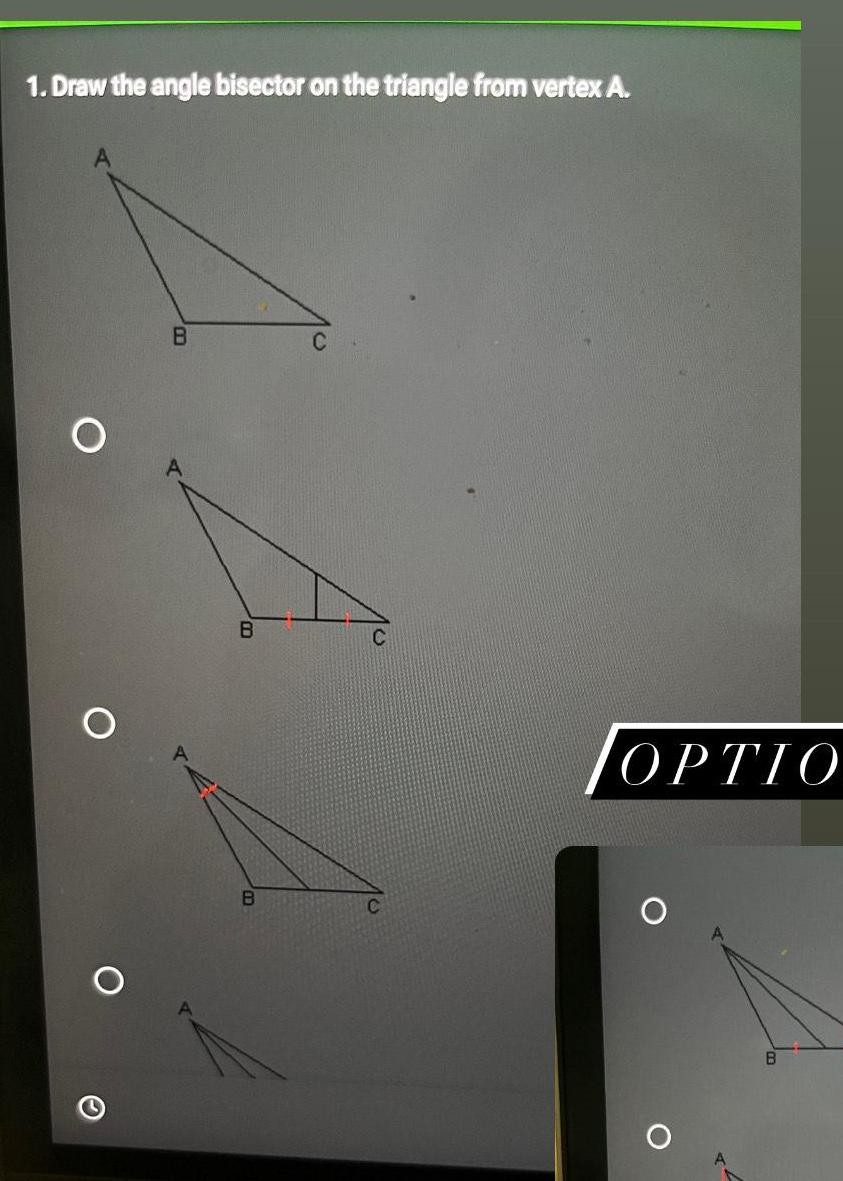
Geometry
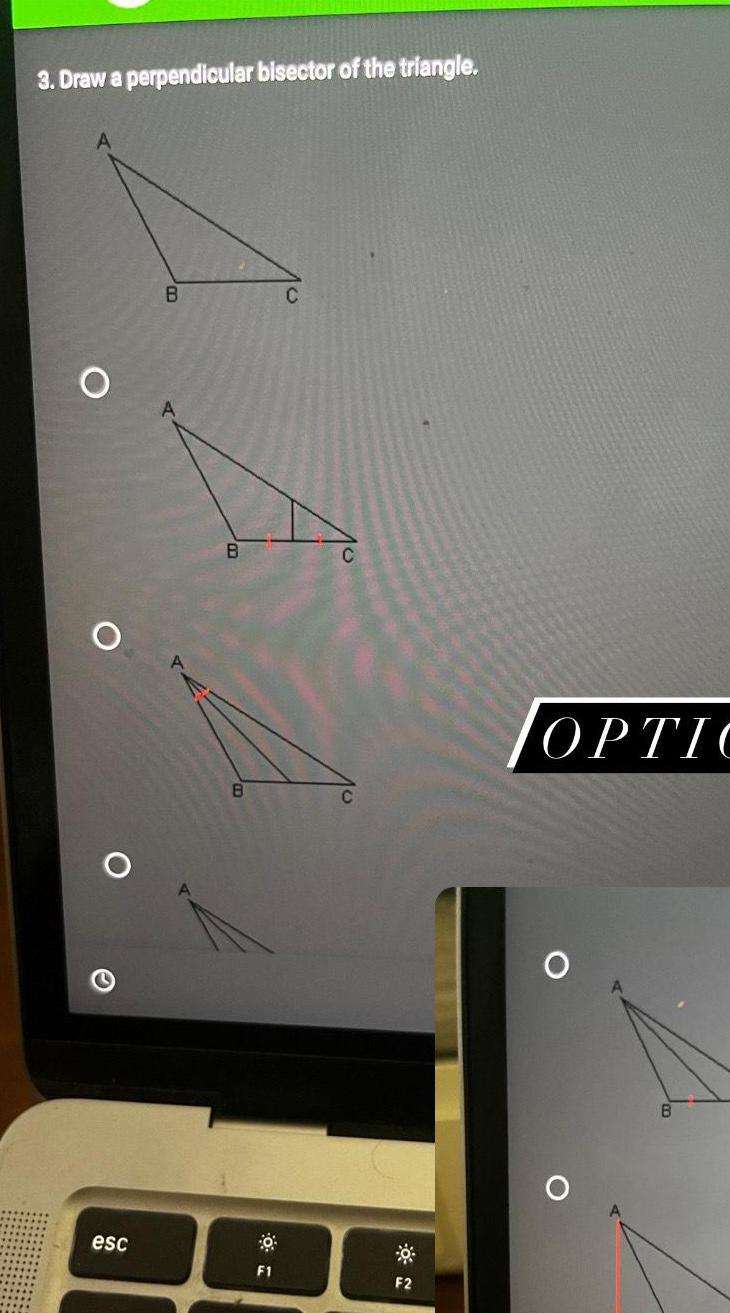
Solution of triangles1 Draw the angle bisector on the triangle from vertex A O O O B B B C OPTIO

Geometry
2D GeometryGraph y x 2 and y 3x on the same set of coordinate axes Use the graphs to find the exact solutions to the equation x 2 3x Then find the solutions using an algebraic method
Geometry
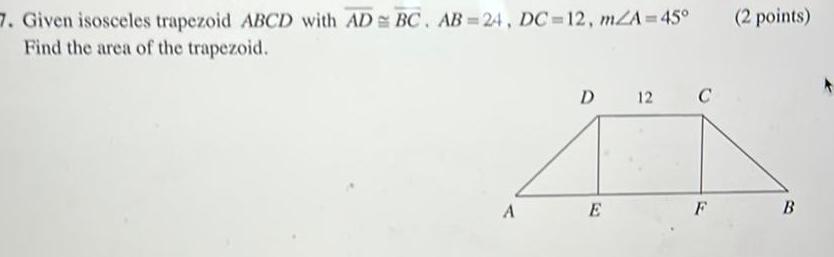
2D Geometry7 Given isosceles trapezoid ABCD with AD BC AB 24 DC 12 m A 45 Find the area of the trapezoid A D 12 E C F 2 points B

Geometry
Area4 Find the area of the quadrilateral ABCD AB 15 AD 9 BC 5 CD 13 2 points B 50 C 15 13 A 9

Geometry
2D Geometry12 In a regular square pyramid the sides of the base measure s 10 cm each and the slant height measures 113 cm 2 points Find the volume of the pyramid V Bh where B is the base area s 10 h 1 13 2 11 5

Geometry
Area3 Given kite ABCD with diagonal AC 10 cm m ABD 30 m ADB 45 Find the area of the kite 3 points B 30 E A C 45 D


Geometry
Area8 Find the area of the regular hexagon whose sides have length s 8cm and apothem a 4 3 cm 2 points s 8cm
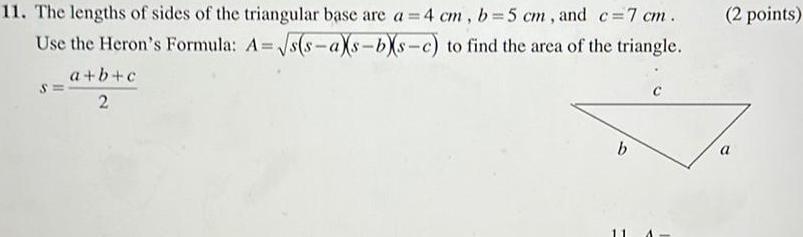
Geometry
Solution of triangles11 The lengths of sides of the triangular base are a 4 cm b 5 cm and c 7 cm s s aXs bs c to find the area of the triangle Use the Heron s Formula A a b c 2 b 2 points a
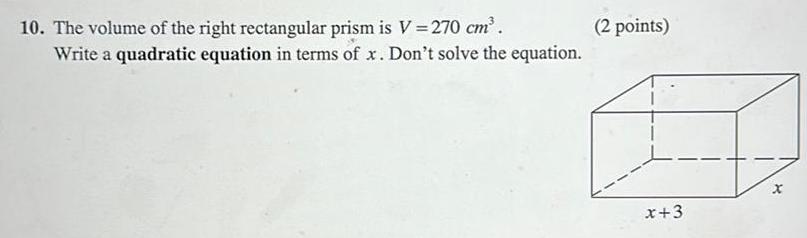
Geometry
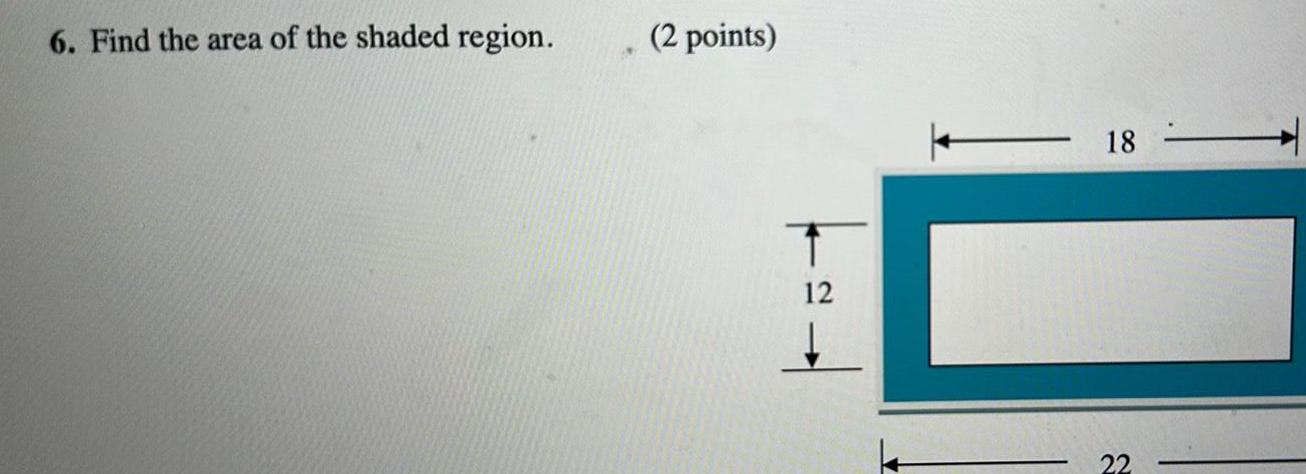
Heights & Distances10 The volume of the right rectangular prism is V 270 cm Write a quadratic equation in terms of x Don t solve the equation 2 points x 3

Geometry
3D Geometry9 Find the exact area of the sector Radius of the circle r 12 cm and m AOB 135 A 12 0135 2 points B

Geometry
2D GeometryPlease show your work No credit will be given for answers 1 Find the area of the rectangle ABCD if AB 30 cm AC 34 cm D 2 point C
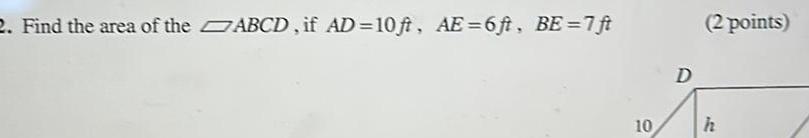

Geometry
Solution of triangles1 Suppose we want to solve the cubic x Ax Bx C 0 To use our algorithm we make the substitution x u A 3 to get a cubic polynomial in u that has no square term This is called completing the cube We then use our algorithm to solve this cubic by using a circle centered at a b Solve for a and b in terms of A B and C 2 The length 2 cos 2 13 is a root of p x x ax x a 1 where a is the larger root of q x x x 3 What center a b should we use to solve the cubic Note that the center is constructible using
Geometry
Coordinate systemShelby invests 300 in a bank account that earns a fixed 4 interest compounded annually The amount in the account after t years is given by f t 300 1 04 Graph this function on your calculator in an appropriate window Label each axis use an appropriate scale and label three points on the graph 3pt Please select file s Select file s Does f t have an inverse function Explain why using the graph 1pt Pick and write down one ordered pair of the inverse function and give its practical

Geometry
Coordinate systemA railroad bridge is built over a V shaped canyon If the supports are 2 feet long at each end the center support is 518 feet long and the supports increase in length by 4 feet with each support from 2 feet to 518 feet what is the total length of all the supports 67 078 ft O 67 082 ft 67 080 ft O 67 086 ft

Geometry
AreaFor an object in an elliptical orbit around the moon the points in the orbit that are closest to and farthest from the center of the moon are called perilune and apolune respectively These are the vertices of the orbit The center of the moon is at one focus of the orbit A spacecraft was placed in a lunar orbit with perilune at a 89 mi and apolune at b 258 mi above the surface of the moon Assuming that the moon is a sphere of radius 1075 mi find an equation for the orbit of this spacecraft Place the coordinate axes so that the origin is at the center of the orbit and the foci are located on the x axis Round each answer to the nearest whole number x X apolune y2 b X 1 moon perilune
Geometry
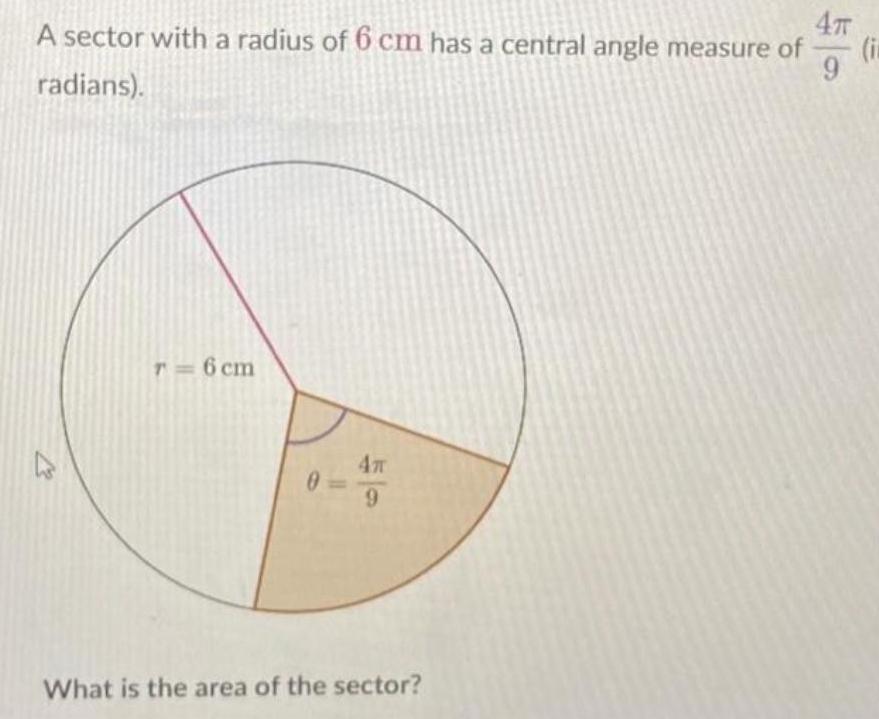
Area4T A sector with a radius of 6 cm has a central angle measure of i 9 radians r 6 cm 0 4T 9 What is the area of the sector

Geometry
2D Geometry1 The ratio of the sides of a triangle is 2 6 7 If the perimeter of the triangle is 195 meters what is the length of the longest side

Geometry
Coordinate systemSolve the problem A forest ranger at Lookout A sights a fire at a bearing N35 W of her position Another ranger at Lookout B exactly 2 kilometers directly west of A sights t same fire at a bearing of N41 E How far is the fire from Lookout A Round your answer to the nearest 0 01 km O 1 35 km O 1 18 km O 1 56 km O 1 69 km