Coordinate system Questions and Answers

Geometry
Coordinate system9 This design began from the construction of a regular hexagon Describe a rigid motion that will take the figure onto itself F A G B C



Geometry
Coordinate systemCreate a single BPMN diagram using the Camunda Modeler of the below process narrative Feature appropriate pools and lanes to represent the different entities participants and the message flows between these entities participants Please label all flows sequences messages Do not use sub processes Canvas is a leading provider of LMS Learning Management Software software Canvas is used by many colleges as a teaching course portal

Geometry
Coordinate systemWrite a function based on the given parent function and transformations in the given order Parent function y H 1 Shift 2 5 units to the right 2 Shrink horizontally by a factor of 3 Reflect across the y axis The function based on the given parent function and transformations in the given order is y 23
Geometry
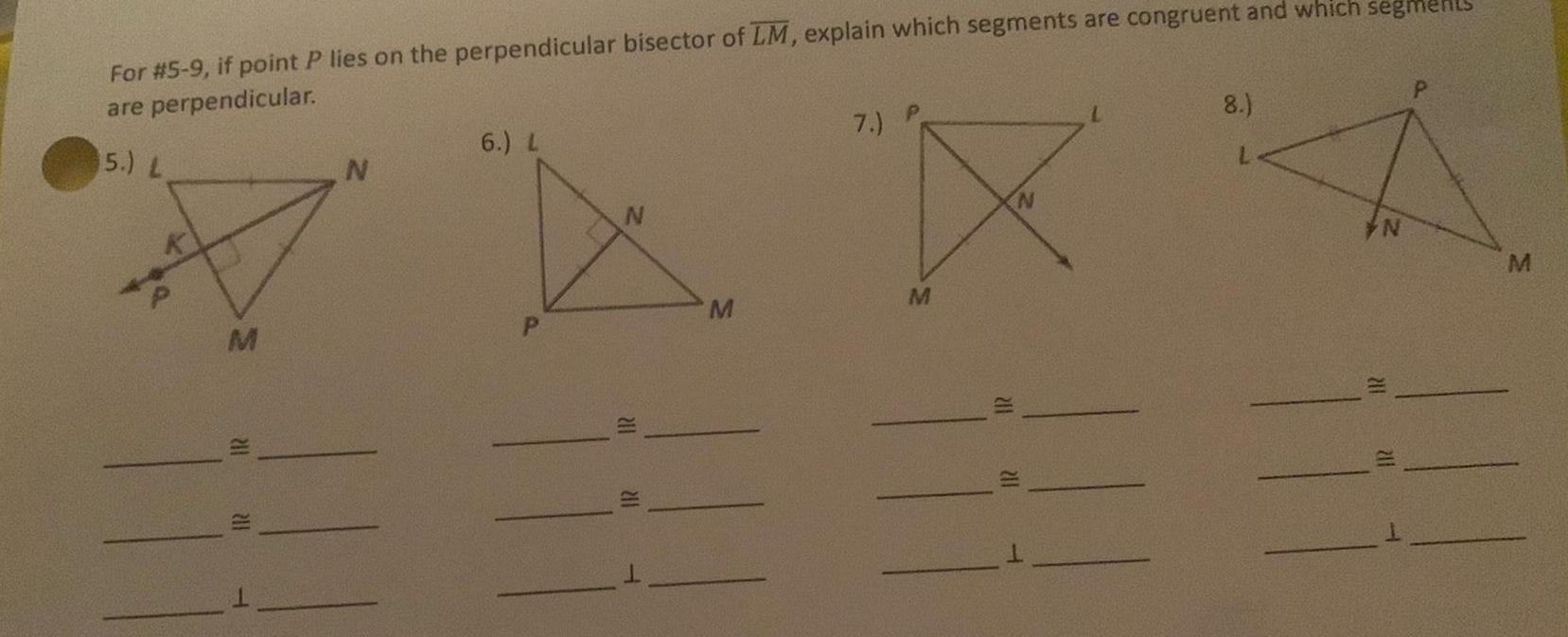
Coordinate systemFor 5 9 if point P lies on the perpendicular bisector of LM explain which segments are congruent and which segmen are perpendicular 5 L M 201 211 N 6 L 211 211 M 7 P M 211 N 211 T 8 L N 211 211 P M
Geometry
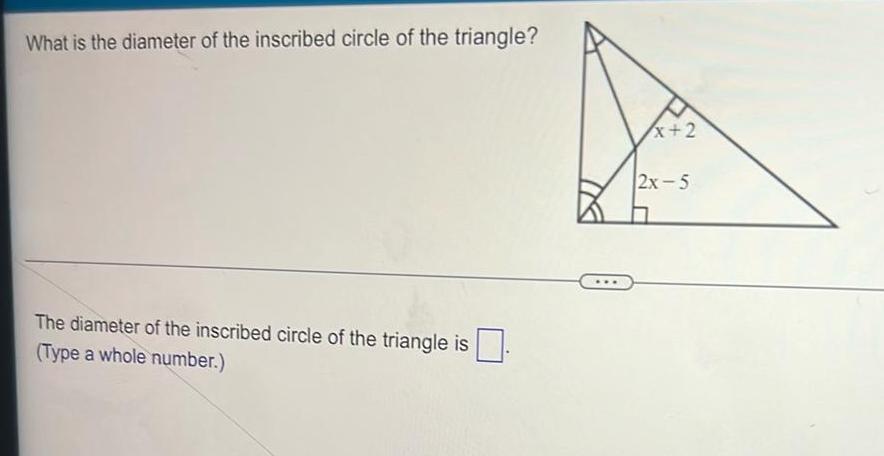
Coordinate systemWhat is the diameter of the inscribed circle of the triangle The diameter of the inscribed circle of the triangle is Type a whole number x 2 2x 5
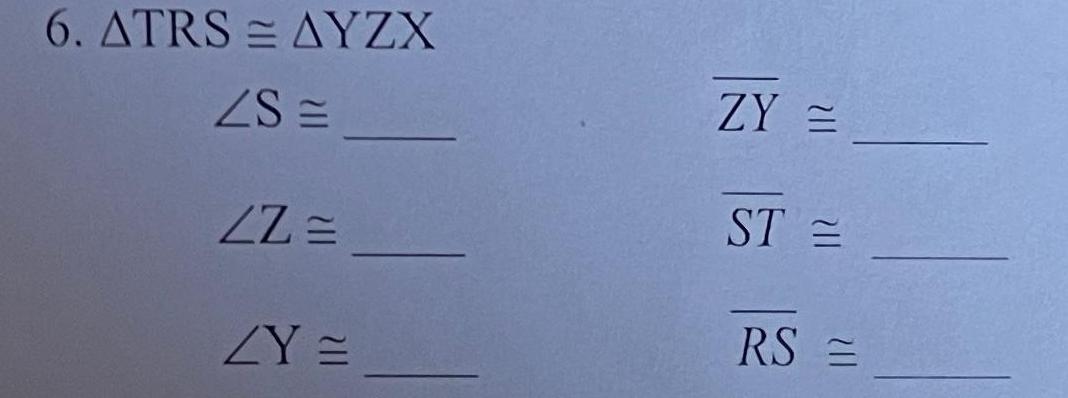

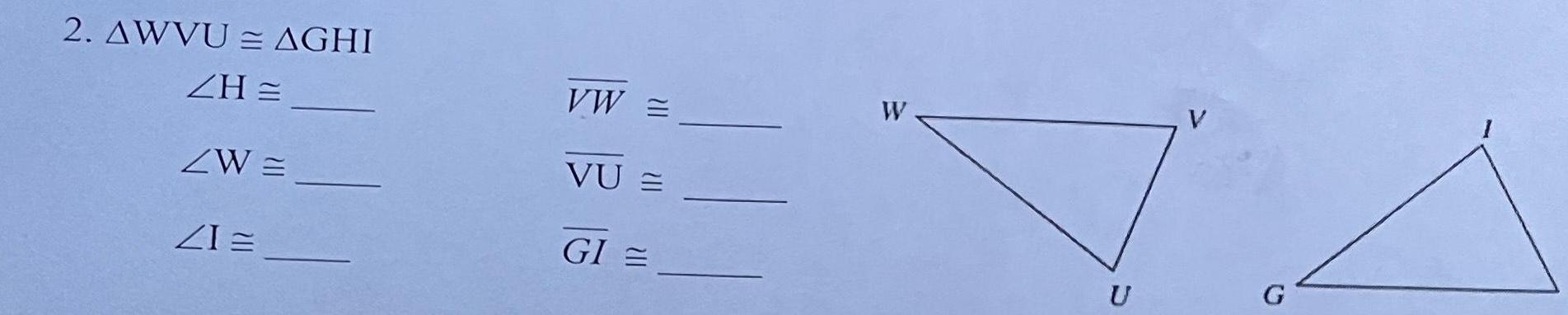
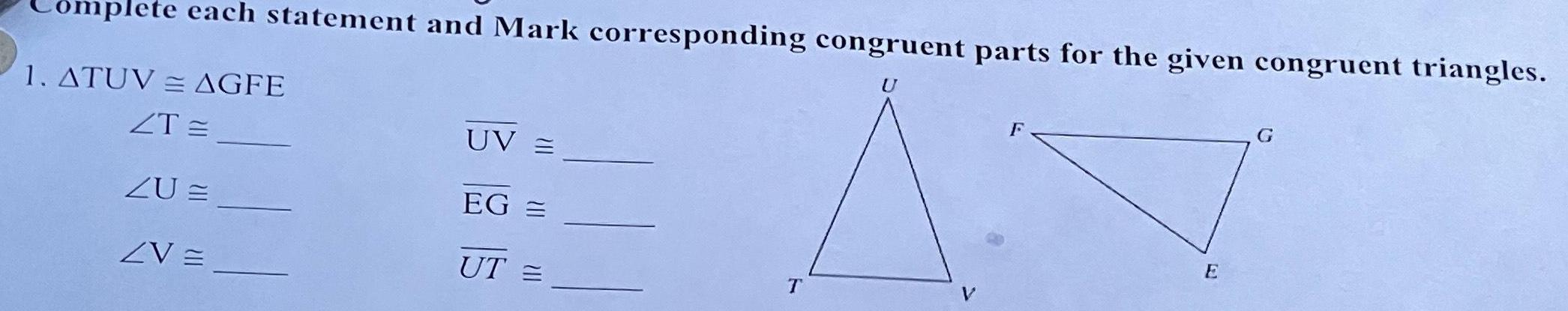
Geometry
Coordinate systemomplete each statement and Mark corresponding congruent parts for the given congruent triangles 1 ATUV AGFE ZT ZU ZV UV EG UT T F E

Geometry
Coordinate systemUse the power spectral density P n4f generate stochastic processes s mT having this energy distribution where T is the sampling period and M the desired number of signal samples in time This is easily done through the following equation s m 7 2 df P n cos 2 n df m T p n 0 Where s m T The stochastic process df frequency resolution fs N P n the PSD mT the amount of time covered for m samples Random phase from U 0 2 where each is drawn from U 0 2 The square root is necessary to transform from power to voltage The factor of one half takes into consideration that power spectra of real signals are symmetric in frequency and only positive frequencies are used in this formulation Multiplication by the sampling period Tscales the power to the correct level Keep in mind that computers don t know absolute time and frequency Therefore example P naf is the nth PSD value in a vector Like the cosine about is the mth element of a vector of length M Labeling frequency axes and time axes requires your consideration and DSP expertise The amplitude of synthesized signals may differ from original ones provided but their characteristics should look the same Provide plots of the signals that you synthesize Comment on their similarity or difference from the provided signals Provide your source code

Geometry
Coordinate systemWhat is the slope of the line that passes through the points 8 6 and 11 12 Write your answer in simplest form Answer Attempt 1 out of 5 ubmit Answer

Geometry
Coordinate systemYour Turn Given Lines l m and n are the perpendicular bisectors of AB AC and BC respectively P is the intersection of lines l m and n From the previous page use the Paragraph Proof of the Circumcenter Theorem to write two column proof of the Circumcenter Theorem Refer to the reason bank below Prove PA PB PC Two Column Proof of the Circumcenter Theorem Statements 1 Lines l m and n are the perpendicular bisectors of AB AC and BC respectively P is the intersection of lines l m and n 2 3 PA PB 4 PB PC 5 PA PB PC Reason Bank Reasons 1 2 3 4 5 E

Geometry
Coordinate systemHW OA OB C OD ework Complete problems 1 3 below for independent practice 1 Which statement correctly describes the perpendicular bisector construction below RO Construction of TS to bisect QR Midpoint between point S and T Construction of QR to bisect ST Midpoint between point Q and R 10 When you are finished check the solutions with your teacher 3 DX EX FX are perpendicular bisectors of AABC Select two options that are true B 12 D F 8 C 2 Which statement correctly describes the perpendicular bisector construction below G A Construction of GH to bisect JK B Midpoint between point J and K OC Midpoint between point G and H OD Construction of JK to bisect GH XC 10 BX 12 CAC 20 BA 24 A OB H OD Optional Complete problems 5 7 15 from your textbook on separate lined paper When you are finished check the odd problems for solutions at the back of the textbook

Geometry
Coordinate systemDetermine which translations would map Figure W onto Figure X Press try to test a translation or sequence of translations A translation 12 11 10 8765 units and Figure X W Figure W 3 2 2 3 4 5 6 7 8 9 10 11 12 4 5 6 10 11 12 units

Geometry
Coordinate systemLesson 4 Practice Problems 1 Angle ABC is taken by a dilation with center P and scale factor 3 to angle A B C The measure of angle ABC is 21 What is the measure of angle A B C 2 Select all lines that could be the image of line m by a dilation A C B m C n D 0 E p 0 l m n P K

Geometry
Coordinate systemSolve the following trigonometric equations for all solutions Enter exact answers whenever possible Choose th smallest positive angle for your base angle a sin 0 3 Solution with smaller positive base angle 0 n for all integers n Solution with larger positive base angle 0 n for all integers n b cos 0 4 Solution with smaller positive base angle 0 1 n for all integers 7 Solution with larger positive base angle 0 nto for all integers n

Geometry
Coordinate systemPart 4 6 Let x 2 x 1 2 a Find the vertex b Find x intercepts zeros c Graph f x by plotting the points from parts a and b

Geometry
Coordinate systemStep 1 Given Information A dot plot for so simulated player took 30 shots is Step 2 a games To given in which a out a simulation to estimate the carry probability that a 50 shooter who took 30 shots in a game would have a streak of 10 or more made shots first need to the assign numbers to the outcomes Let 1 represent the made shot and 2 represent the missed shot Now generate 30 random digits from 1 to 2 Record whether there is a sequence of at least 10 made shots or not Repeat the

Geometry
Coordinate systemYour Turn 2 Use the figure to find the mzM Lesson 7 2 Ch 3 Use the figure to find the mzP N 7y 4y 15 M 3x 3 R 5x 2




Geometry
Coordinate systemWrite a two column proof 1 Given EF FH ZE ZH Prove HG DE D G E F H Statement Reason

Geometry
Coordinate systemStep 1 We want to find the exact value of sin 3r From the text the quadrants are numbered counter clockwise from the upper right I II III IV This angle lies in quadrant 111 III 11 4 3 To find that value we first have to draw the angle Step 2 Sketching the angle we draw the triangle formed with the terminal side and the y axis Looking at this triangle we see that it is a triangle xxx Likewise the opposite side should be labeled 3A From the text we know that the side lengths are 2 2 2 To label the sides with the proper lengths we note that 2 being the longest side length must be the hypotenuse The smallest angle will be opposite the shortest side Looking at the triangle and taking into account the quadrant so that the sign is correct the adjacent side should be labeled

Geometry
Coordinate systemFor use with pages Find the angle measure Tell which postulate or theorem you use 1 If m1 50 then m 5 2 If m 4 45 then m26 3 If m 2 130 then m 7 4 Ifm 6 123 then m 3 2 3 4 519 7 6 8

Geometry
Coordinate system4 A pilot is flying over a straight highway He determines the angle of depression to two mile posts 2 1 km apart to be 25 and 49 as shown in the figure below Find the distance of the plane from point A and find the elevation of the plane 125 49 A B

Geometry
Coordinate systemFor the following exercises assume a is opposite side a is opposite side b and is opposite side c Solve each triangle if possible Round each answer to the nearest tenth 1 B 50 a 105 b 45

Geometry
Coordinate systemFind all of the solutions to the equation in the interval 0 2 2 sin r1 esc z

Geometry
Coordinate systemFind the standard form of the equation of the hyperbola with the given characteristics Vertices 3 5 3 11 Asymptotes y x 6 y x

Geometry
Coordinate systemFind the center vertices and foci of the hyperbola y 3 x 4 x 4 9 center x y vertices x y foci x y x y x y 1 smaller y value larger y value 2 smaller y value Find the asymptotes of the hyperbola Enter your answers as a comma separated list of equations 4 larger y value Sketch its graph using the asymptotes as an aid Use a graphing utility to verify your graph y 8 6 4 2 2 X 6 8 X X 2 6 4 2 2 4 2 8 8 X

Geometry
Coordinate systemConsider the following 4x 9y 24x 90y 198 0 a Find the standard form of the equation of the hyperbola If the hyperbola is degenerate enter NONE b Find the center vertices foci and asymptotes of the hyperbola If the hyperbola is degenerate enter NONE in each answer blank Center Vertices Foci Asymptotes y negative slope positive slope c Select the correct graph of the hyperbola using the asymptotes as an aid Use a graphing utility to verify your answer A 4 10 6

Geometry
Coordinate systemFind the standard form of the equation of the hyperbola with the given characteristics Vertices 14 0 foci 7 0

Geometry
Coordinate systemHan invests 13 000 into a fund that combines stocks and bonds The return varies from year to year The balance at 5 year intervals is given in the table below The goal of this exercise is to find constants a and b such that the model y ae best fits the data In order to do that we apply the natural logarithm to both sides of the model This yields In y n a and using properties of logarithms weet T lex be and the problem now reduone to finding the Pcjwey In y In a In ee In y In a bt If we let Y In y c In a and c b the problem now reduces to finding the linear fit Y q c the set of dats points Part b t 0 5 10 15 20 25 y Balance 1 000 13 14 5 16 18 2 19 9 22 3 5 10 FLO 18 31 115 11451 lec16 In 1821 In 199 Find the cheskydecompcation of S and store in U Soke thener system w me sing the backataah command Solve the langur system cw using the backslash command Compute the best fit use 25 2231 art a The sectors and y have already been created for you Compute the sector by evaluating the natu ofy note that the natural logam entered a lng in MATLAB Create the mote X for the rear Create the tor 2 Create the magic I Plot the date pents and upper case Use o to plot points by the original data polts Use Lindth 2 und is that you por Use Inestyle and color the line back gure by tyckig hold off Computand where and are the values you found in part 4 Se the wi coobies a widespectively Ente figure to open a new gu plot the original data points and lower cass no toplot points

Geometry
Coordinate systemComplete the proof of the identity by choosing the Rule that justifies each step sec x tan x 1 To see a detailed description of a Rule select the More Information Button to the right of the R Statement sec x tan x 1 tan x tan x Rule Rule

Geometry
Coordinate systemFind the standard form of the equation of the parabola with the given characteristics Vertex 7 6 directrix x 14

Geometry
Coordinate systemQuestion 8 th B C 2x 41 S 61 Which of the following is the value of PQ A 46 67 D 91 3x 16 7x24 Pause Q Zoom 4

Geometry
Coordinate systemRead the question and enter your response in the box provided Use the tools and your keyboard to construct your response In the diagram line I and line m are parallel m 4 7x 5 and m25 5x 27 Solve for 778 1 7 8 6 4 5 1 3 2

Geometry
Coordinate systemGiven PIIQ and T is a transversal which of the following justifies 23 26 2023 A B C D 5 6 8 2 4 Q Corresponding Angles Postulate Alternate Interior Angles Theorem Consecutive Interior Angles Theorem Alternate Exterior Angles Theorem Illuminate Education TM Inc

Geometry
Coordinate systemQuestion 8 If ACDE were reflected across the line y x what would be the coordinates of ACD E 8 6 4 2 co 6 A 2 2 4 6 14 C 2 6 8 D E

Geometry
Coordinate system8 6 4 2 A B C D 2 4 6 C 2 4 8 D E x 8 C 1 5 D 8 2 E 7 6 C 1 5 D 8 2 E 7 6 C 1 5 D 8 2 E 7 6 C 5 1 D 2 8 E 6 7

Geometry
Coordinate systemQuestion 7 Triangle ABC is reflected over the line y 1 to produce triangle A B C 8 6 2 6 4 2 1 2 4 4 2 2 B 6 4 1 8 A

Geometry
Coordinate systemE 10 8 6 4 2 O E A B C D F 8 co 6 41 G 2 2 A 16 10 2 4 6 8 10 G x y x 4 y 11 x y x 4 y 11 x y r 11 y 4 x y x 11 y 4


Geometry
Coordinate systemIn Silicon Valley a number of computer firms were found to be contaminating underground water supplies with toxic chemicals stored in leaking underground containers A water quality control agency ordered the companies to take immediate corrective action and contribute to a monetary pool for the testing and cleanup the underground contamination Suppose that the required monetary pool in millions of dollars is given by the following function where x is the percentage expressed as a decimal fraction of the total contaminant removed Complete parts A through E P x 3x 1 x OA The x intercept s is are x Simplify your answer Use a comma to separate answers as needed OB There are no x intercepts Find the y intercept s Select the correct choice below and if necessary fill in the answer box to complete your choice A Simplify your answer Use a comma to separate answers as needed OB There are no y intercepts E Sketch a graph of P x Choose the correct graph below OA OA The y intercept s is are y 0 x 1 APDO 50 0 A Q Q OB APDO 50 14 GEXED Q 12 OC AP X Q LL Q OD 50 APDO Q Q G


Geometry
Coordinate systemA propery is being transported through a fhuid a steady state through a constant coss sectional area At point the concentration is 278 x 102 amount of property m and 1 50 x 10 at point 2 at adistance of 20 m away Thedificivity depends on concentration as 80150 14651 a Calculate the steady state fua if the two points were separated by 35 m but with the same concentrators How does the flux vary with the distance between the points Calculate the steady state flux if the concentration at point 2 was 150 x 10 amount of property using the nigral disance 2 0 m How does the way with th diference in concentration b

Geometry
Coordinate system2 Let 0 be an acute angle Complete the following table 0 30 45 60 sin 0 COS A tan 0

Geometry
Coordinate systemA property is being transported through a fuil at steady state through a constant cros sectional area at point the concertation is 278 x 10 amount of property and 150 x 10 point 2at a distance of 20 m away The difusity depends on concentration las 0 150 1 65 b a Calculate the steady state for the two points were separated by 35 m but with the same concentrations How does the fux vary with the distance between the points Calculate the steady state fluxif the concentration at point 2 was 150 x 10 amount of property m using the orgina distance 2 0 m How does the fu vary with he diference in concentration