Math Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Math
StatisticsComplete parts (a) and (b) below. The number of dogs per household in a small town
Dogs 0 1 2 3 4 5
Probability 0.649 0.084 1 0.226 3 0.022 0.013 0.006
Find the variance of the probability distribution. σ2 = (Round to one decimal place as needed.)
Find the standard deviation of the probability distribution. σ= (Round to one decimal place as needed.)
(b) Interpret the results in the context of the real-life situation.
A. A household on average has 0.5 dog with a standard deviation of 0.9 dog.
B. A household on average has 0.8 dog with a standard deviation of 0.9 dog.
C. A household on average has 0.9 dog with a standard deviation of 0.5 dog.
D. A household on average has 0.5 dog with a standard deviation of 11 dogs.

Math
Basic MathUsing the data given below, determine whether it would unusual for a household to have no HD televisions. The number of televisions (HD) per household in a small town
Televisions 0 1 2 3
Households 52 460 668 1420
P(x) 0.020 0.177 0.257 0.546
Choose the correct answer below.
A. It would not be unusual because the probability of having no HD televisions is more than 0.05.
B. It would not be unusual because 52 people have no HD televisions in the town. C. It would be unusual because 52 people have no HD televisions in the town.
D. It would be unusual because the probability of having no HD televisions is less than 0.05.

Math
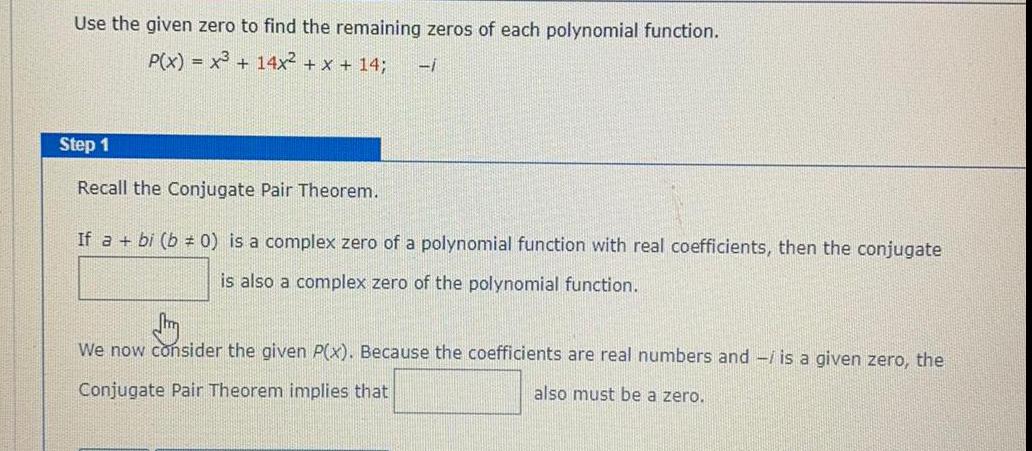
Complex numbersUse the given zero to find the remaining zeros of each polynomial function.
P(x) = x³ + 14x² + x + 14;
Step 1
Recall the Conjugate Pair Theorem.
If a + bi (b ≠ 0) is a complex zero of a polynomial function with real coefficients, then the conjugate is also a complex zero of the polynomial function.
We now consider the given P(x). Because the coefficients are real numbers and - is a given zero, the Conjugate Pair Theorem implies that ___also must be a zero.

Math
StatisticsFinal marks in Maria's Data Management course are based on 70% for term work,
15% for the exam, and 15% for the final course project. What term mark did Maria
receive if her final mark was 87% and she received 84% on the exam and 95% on her final project?
a) 87%
b) 83%
c) 85%
d) 86%
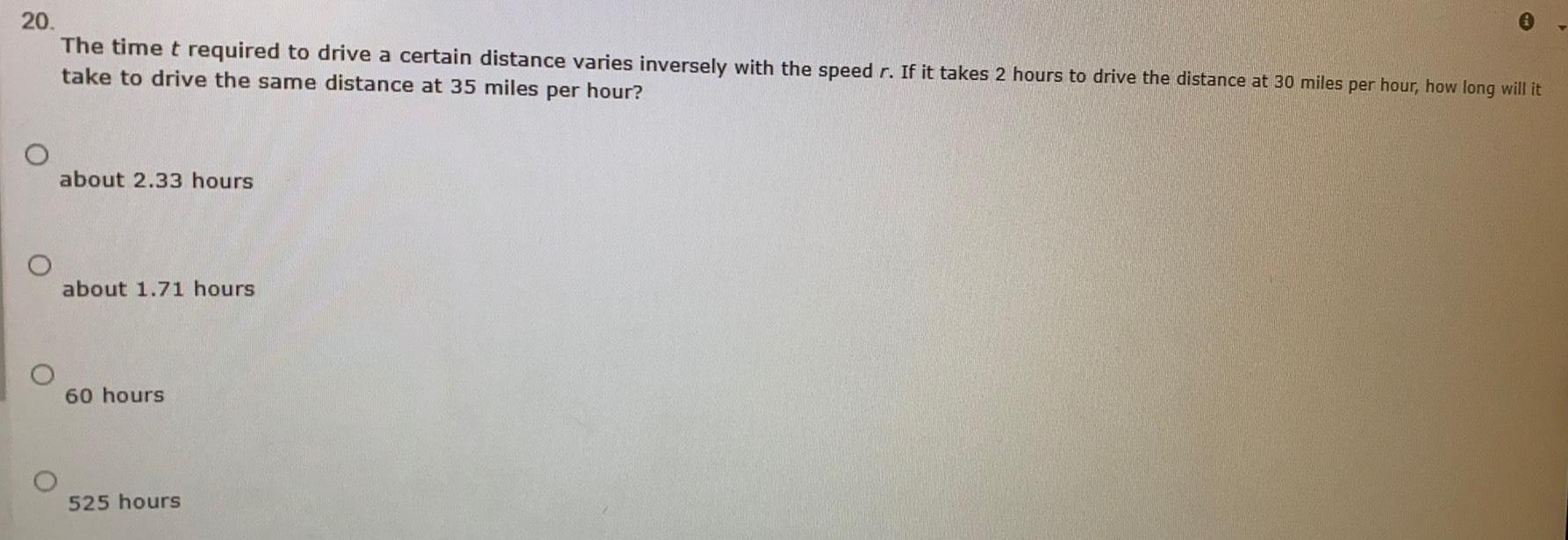
Math
Basic MathThe time t required to drive a certain distance varies inversely with the speed r. If it takes 2 hours to drive the distance at 30 miles per hour, how long will it
take to drive the same distance at 35 miles per hour?
about 2.33 hours
about 1.71 hours
60 hours
525 hours

Math
Basic Math2. Which of the following could be represented by a periodic function? Explain your answer.
a. the average monthly temperature in your community, recorded every month for three years
b. the population in your community, recorded every year for the last 50 years
c. the number of cars per hour that pass through an intersection near where you live, recorded for two consecutive school days
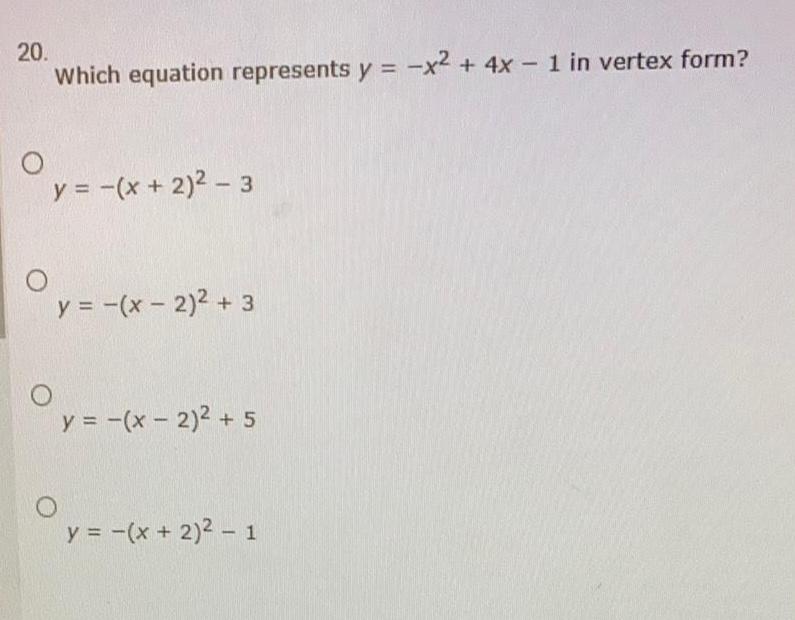
Math
Basic MathWhich equation represents y = -x² + 4x - 1 in vertex form?
y = -(x + 2)² - 3
y = -(x - 2)² +3
y = -(x - 2)² + 5
y = -(x + 2)² - 1

Math
ProbabilityThree letters are to be selected at random from the English alphabet of 26 letters. Determine the probability that 3 consonants are selected. Assume there are 21
consonants in the alphabet and that selection is to be done without replacement.
Set up the problem as if it were to be solved, but do not solve.
P(3 consonants selected) =
![The cost to remove a toxin from a lake is modeled by the function C(p) = 75p/85-p where C is the cost (in thousands of dollars) and p is the amount of toxin in a small lake (measured in parts per billion [ppb]).
This model is valid only when the amount of toxin is less than 85 ppb.
a. Find the cost in dollars to remove 45 ppb of the toxin from the lake.
(round to the nearest whole dollar)
C=S
b. Find the formula for the inverse function.
p=f¹(C)=
c. Use part b. to determine how much toxin is removed for $60,000.
ppb (round to 2 decimal places)](https://media.kunduz.com/media/sug-question/raw/52816524-1658424281.2470524.jpeg?w=256)
Math
Basic MathThe cost to remove a toxin from a lake is modeled by the function C(p) = 75p/85-p where C is the cost (in thousands of dollars) and p is the amount of toxin in a small lake (measured in parts per billion [ppb]).
This model is valid only when the amount of toxin is less than 85 ppb.
a. Find the cost in dollars to remove 45 ppb of the toxin from the lake.
(round to the nearest whole dollar)
C=S
b. Find the formula for the inverse function.
p=f¹(C)=
c. Use part b. to determine how much toxin is removed for $60,000.
ppb (round to 2 decimal places)

Math
FunctionsThe position (in feet) of a buoy in the water can be modeled by the function
s(t) = 9 cos(t) where t is the elapsed time in seconds.
(a) If we start viewing the buoy when it is at its high point, how many seconds does it take
until the buoy is back at the high point again (i.e. What is the period of the function?)

Math
ParabolaWhich of the following describes the parabola with the equation y = 4x² - 12x + 9?
The axis of symmetry is x = -1.5 and the vertex is (-1.5, 36).
The axis of symmetry is x = 4 and the vertex is (4, -12).
The axis of symmetry is x = 0 and the vertex is (0, 9).
The axis of symmetry is x = 1.5 and the vertex is (1.5, 0).

Math
Basic MathWhy was Carnegie Steel considered a vertical monopoly?
The company controlled every step of steel production, from raw materials to distribution.
The company controlled all the steel plants in the country.
The company became the only source of steel after competitors went out of business.
The company was able to produce more steel than any other steel company in the world.

Math
Quadratic equationsUse the quadratic model d= -3p2 + 168p 315 to predict d if p equals 15.
1845
2160
2880
1530

Math
StatisticsThe following numbers show the temperature, in degrees Celsius, of coffee in 30
recently tested coffee makers: 76 68 72 73 70 69 68 73 81 72 66 85 72 72 69 72
67 74 73 69 75 65 70 71 71 71 68 74 79 73
Calculate the mean, median and mode.
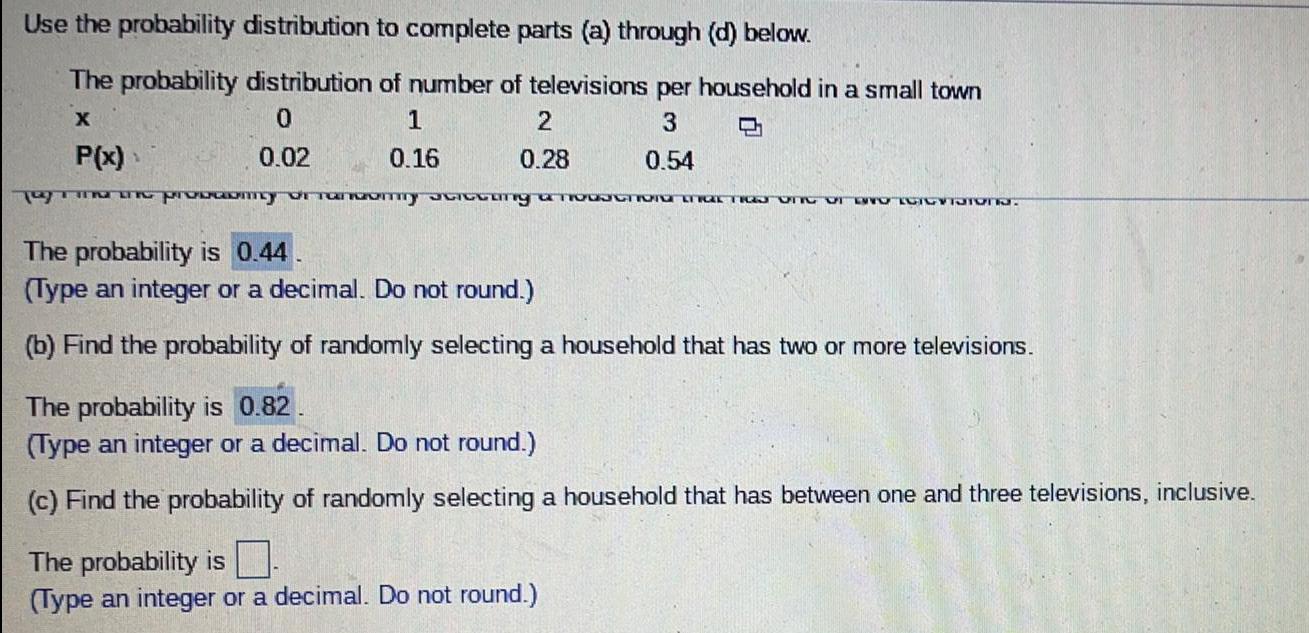
Math
ProbabilityUse the probability distribution to complete parts (a) through (d) below.
The probability distribution of number of televisions per household in a small town
The probability is
(Type an integer or a decimal. Do not round.)
(b) Find the probability of randomly selecting a household that has two or more televisions.
The probability is
(Type an integer or a decimal. Do not round.)
(c) Find the probability of randomly selecting a household that has between one and three televisions, inclusive.
The probability is
(Type an integer or a decimal. Do not round.)

Math
Basic MathWhich of the following is a
geometric sequence?
Enter a, b, c, d, or e.
a. 4, 12, 36, 108, 324,
b. 2, 4, 16, 256, 65536, ...
c. 4, 17, 30, 43, 56, ...
d. 3, 7, 11, 15, 19, ..
e. 1, 2, 4, 10, 12, ...

Math
Basic MathThe following data shows the
weight loss (in pounds) of a
sample of five members in a
health club at the end of two
months of membership.
10 5 19 8 3
Find the median.

Math
FunctionsChoose all that are properties of one-to-one functions.
x-values are repeated.
Functions are always one-to-one.
The graph passes the vertical line test.
y-values are repeated.
y-values are not repeated.
x-values are not repeated.
The graph passes the horizontal line test.
Math
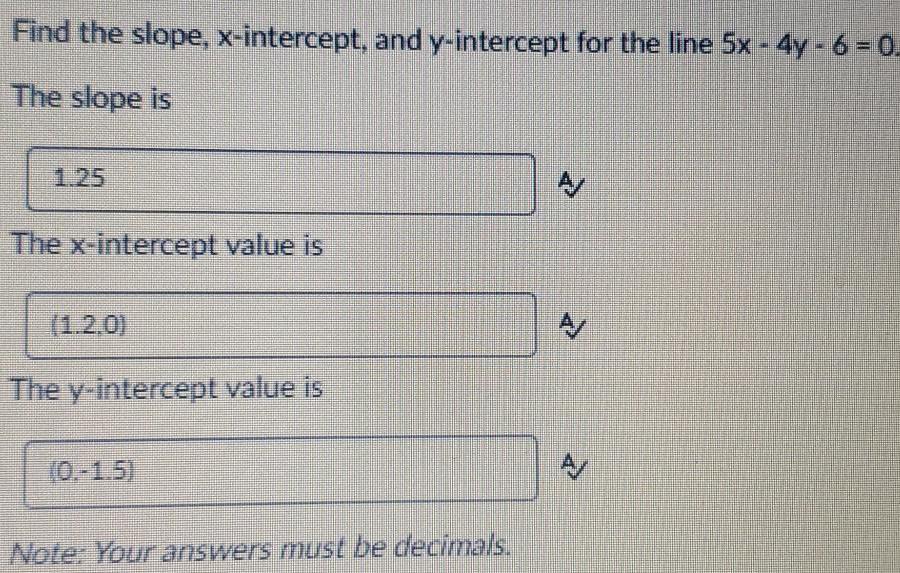
Straight linesFind the slope, x-intercept, and y-intercept for the line 5x - 4y - 6=0.
The slope is
The x-intercept value is
The y-intercept value is
Note: Your answers must be decimals.

Math
ProbabilityAssume that the probability of any newborn baby being a boy is1/2 and that all births are independent. If a family has three children (no twins), what is the probability of the event that none of them are boys? The probability is (Simplify your answer.)

Math
ProbabilityTen red balls and three blue balls are in a bag. If two balls from the bag are to be selected at random, determine the probability of selecting two red balls. Assume that selection is to be done without replacement.
Set up the problem as if it were to be solved, but do not solve.
P(2 red balls selected) =

Math
Basic MathDirections Substitute Equation 1 into Equation 2. Find the value for x, then find the value for y and input your answers in the boxes below.
Equation 1: y = 2x
Equation 2: x+y=6

Math
Basic MathA ball is kicked into the air. It follows a path given by h(t) = -4.9t² +8t+ 0.4, where t is the time, in
seconds, and h(t) is the height, in meters.
a) Determine the maximum height of the ball to the nearest tenth of a meter.
b) When does the ball reach its maximum height?
Math
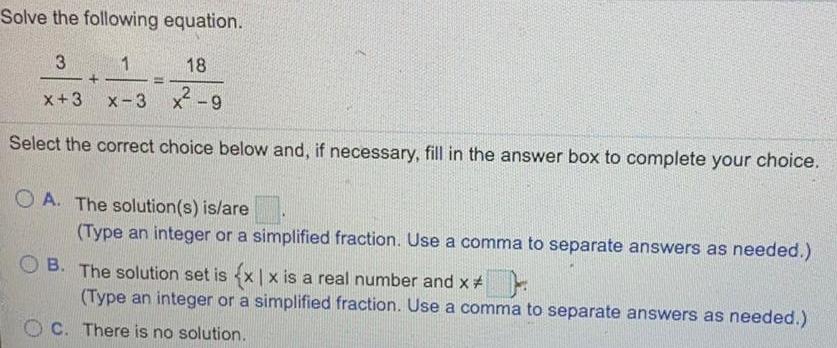
Basic MathSolve the following equation.
3/x+1/x-3=18/ x²-2
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The solution(s) is/are
(Type an integer or a simplified fraction. Use a comma to separate answers as needed.)
B. The solution set is {x|x is a real number and x ≠
(Type an integer or a simplified fraction. Use a comma to separate answers as needed.)
C. There is no solution.

Math
Basic MathWrite an equation that expresses the following relationship: x varies jointly as y and a and inversely as the square root of m. Then solve the equation for y.
Write an equation that expresses the given relationship. Use k as the constant of variation.
x=

Math
Basic MathFind the absolute change and the percentage change in the following case.
The number of daily news paper in a country was 2063 in 1900 and 1312 in 2010.
The absolute change is
(Simplify your answer. Type an integer or a decimal.)

Math
Quadratic equationsThe polynomial of degree 4, P(x) has a root of multiplicity 2 at x = 1 and roots of multiplicity 1 at x = 0 and x = - 4. It goes through the point (5, 72). Find a formula for P(x).
Math
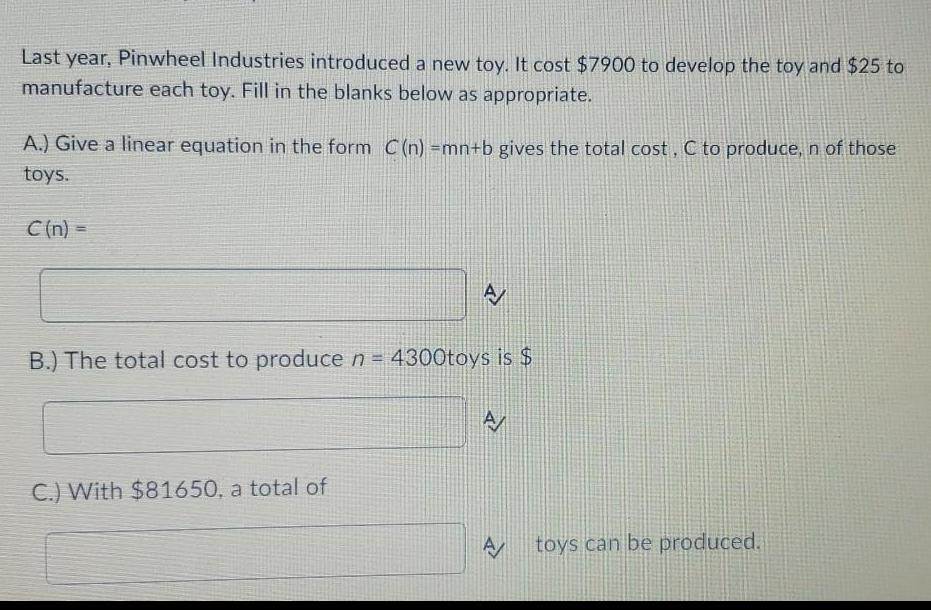
Basic MathLast year, Pinwheel Industries introduced a new toy. It cost $7900 to develop the toy and $25 to manufacture each toy. Fill in the blanks below as appropriate.
A.) Give a linear equation in the form C (n) =mn+b gives the total cost, C to produce, n of those toys.
C (n) =
B.) The total cost to produce n = 4300 toys is $
C.) With $81650, a total of
A toys can be produced.

Math
Straight linesFind the equation of the line, in slope-intercept form, that satisfies the given conditions.
The graph is parallel to the graph of x + 2y = 8 and passes through the point whose coordinates are (-2,-4).

Math
Basic MathWhat is the best way to manage adversity in the workplace?
A) Look for the root cause of the problem.
B) Brainstorm ways the problem can be overcome.
C) Consider the causes and effects of the problem.
D) View the problem as an opportunity to make changes.

Math
Basic MathTo cut costs, the Rose City school board has decided to eliminate art and music courses. Isabella's daughter plans to go to art school after high school and needs access to art courses.
Which action shows that Isabella understands the importance of root cause analysis when wanting to effect change?
A) She meets with the school principal to express her concerns about the decision.
B) She makes a list of why the school board may have decided to drop art and music classes.
C) She asks teachers, students, and parents to sign a petition in favor of keeping art and music classes.
D) She uses social media to boycott the school if the school board does not change its decision.

Math
Sequences & SeriesAn arithmetic sequence is one that involves adding or subtracting by the same number to each term in the sequence.
A geometric sequence is one that involves multiplying or dividing by the same number to each term in the sequence.
Classify each sequence as arithmetic, geometric, or neither. There should be two sequences in each category.
Math
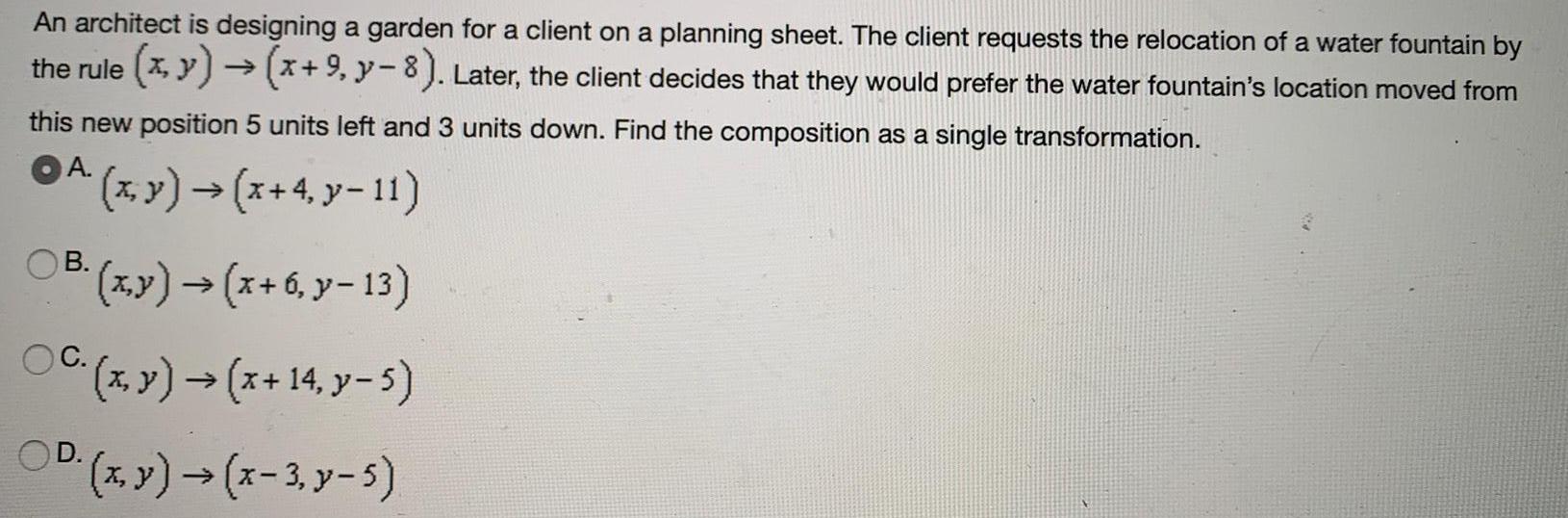
Coordinate systemAn architect is designing a garden for a client on a planning sheet. The client requests the relocation of a water fountain by the rule (x,y) → (x+ 9, y-8). Later, the client decides that they would prefer the water fountain's location moved from this new position 5 units left and 3 units down. Find the composition as a single transformation.
A. (x,y) → (x+4, y-11)
B. (x,y) → (x+6, y-13)
C. (x, y) → (x + 14, y − 5)
D. (x, y) → (x-3, y-5)

Math
Basic MathTo produce the graph of the function Y=0.5cot(0.5x), what transformations should be applied to the graph of the parent function Y = cot(x)?
a horizontal compression to produce a period of π/2 and a vertical compression
a horizontal compression to produce a period of π/2 and a vertical stretch
a horizontal stretch to produce a period of 2π and a vertical compression
a horizontal stretch to produce a period of 2π and a vertical stretch

Math
Permutations and CombinationsThe trifecta at most racetracks consists of selecting the first-, second-, and third-place finishers in a particular race in their proper order. If there are twelve entries in the trifecta race, how many tickets must you purchase to guarantee a win?

Math
3D GeometryThe original photograph shown is 4 inches by 6 inches.
a. What transformations can you use to produce the new photograph?
b. You dilate the original photograph by a scale factor of What
are the dimensions of the new photograph?
c. You have a frame that holds photos that are 8.5 inches by
11 inches. Can you dilate the original photograph to fit the
frame? Explain your reasoning.
Math
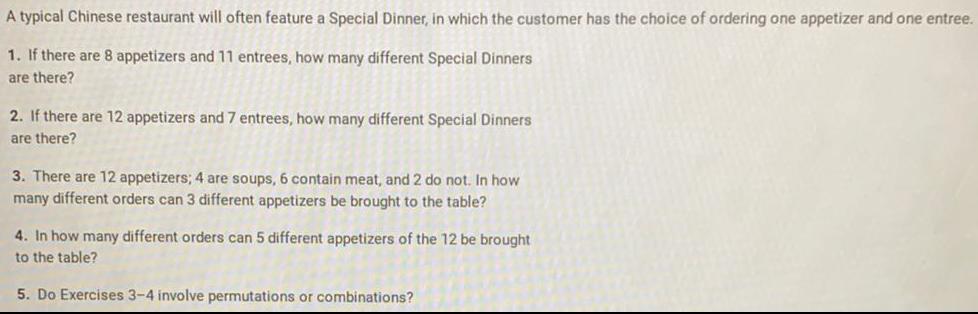
Permutations and CombinationsA typical Chinese restaurant will often feature a Special Dinner, in which the customer has the choice of ordering one appetizer and one entree.
1. If there are 8 appetizers and 11 entrees, how many different Special Dinners
are there?
2. If there are 12 appetizers and 7 entrees, how many different Special Dinners
are there?
3. There are 12 appetizers; 4 are soups, 6 contain meat, and 2 do not. In how
many different orders can 3 different appetizers be brought to the table?
4. In how many different orders can 5 different appetizers of the 12 be brought
to the table?
5. Do Exercises 3-4 involve permutations or combinations?

Math
Basic MathMegan runs a bakery. The amount of profit, in dollars, she makes on every cake she sells is equal to
the function f(M), where f(M)= 5.50N, and Nrepresents the number of cakes she sells.
Determine whether each descretion shown in the table below represents the relationship between
f(M) and Nfor the description given. Select Yes or No to indicate for each description.
Description
If Megan sells 22 cakes, then f(22) = 121
If Megan sells 10 cakes, then f(55) = 10
If Megan sells 2 cakes, then f(2)= 11
Math
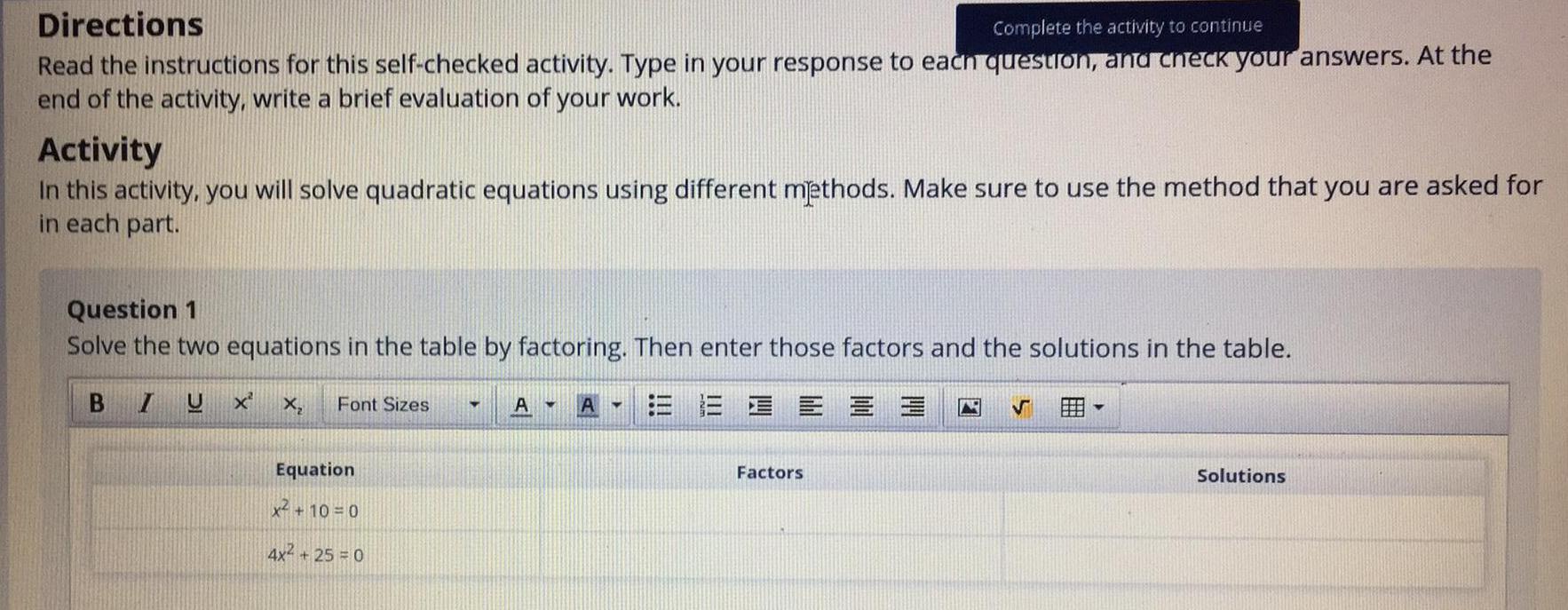
Basic MathDirections
Complete the activity to continue
Read the instructions for this self-checked activity. Type in your response to each question, and check your answers. At the
end of the activity, write a brief evaluation of your work.
Activity
In this activity, you will solve quadratic equations using different methods. Make sure to use the method that you are asked for
in each part.

Math
Basic MathWhich statement shows reasoning that is based on assumption, not fact?
A) Kim does not like doing data entry, and neither do I.
B) Many of my friends like to drink iced tea in the summer, so I will buy some for the party.
C) All project managers have college degrees. Sonya is a project manager, so she has a
college degree.
D) I always round the numbers when making a budget, so everyone must round numbers to
make a budget.


Math
Basic MathA card is drawn one at a time from a
well-shuffled deck of 52 cards. In 13
repetitions of this experiment, 2 kings
are drawn. If E is the event in which
a king is drawn in the 13 trials, find
the experimental probability P(E).

Math
Basic MathHow does the graph of g(x) = 3x - 2 compare to the graph of f(x) = 3x?
The graph of g(x) is a translation of f(x) 2 units left.
The graph of g(x) is a translation of f(x) 2 units right.
The graph of g(x) is a translation of f(x) 2 units up.
The graph of g(x) is a translation of f(x) 2 units down.

Math
Quadratic equationsWhat substitution should be used to rewrite x8-3x4+2=0 as a quadratic equation?
u = x²
u=x4
u=x8
u = x16

Math
Basic MathType your response in the box.
Find the solutions to this system of equations algebraically.
y = x² - 4x + 2
y = 5x - 12

Math
Basic MathThere are eight online songs
that you would like to download,
but you only have enough.
money for three. How many
different groups of songs can
you buy?
![Use: Ck
n
n!
k! (n-k)!
to solve the combination.
How many different combinations of
six people can sit in four chairs?
Assume one person sits in each chair.
[?] ways](https://media.kunduz.com/media/sug-question/raw/52700640-1658422873.191814.jpeg?w=256)
Math
Permutations and CombinationsUse: Ck
n
n!
k! (n-k)!
to solve the combination.
How many different combinations of
six people can sit in four chairs?
Assume one person sits in each chair.
[?] ways

Math
Basic MathWhich statement is true about adaptable workers?
A) They adjust to changes in the workplace easily.
B) They know ways to manage stressful situations.
C) They apply the cycle of inquiry to solve problems.
D) They make decisions with logic and reason.

Math
Basic Math2. The directed line segment ST has endpoints S(-3, -2) and T(4, 5). Point P lies on the directed line segment ST and the ratio of SP to PT is 3 to 4. What are the coordinates of point P?
(F) (0, 1)
(H) (7,8)
(G) (2 1/4, 3 1/4)
(J) (9 1/4 , 10 1/4)