Math Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Math
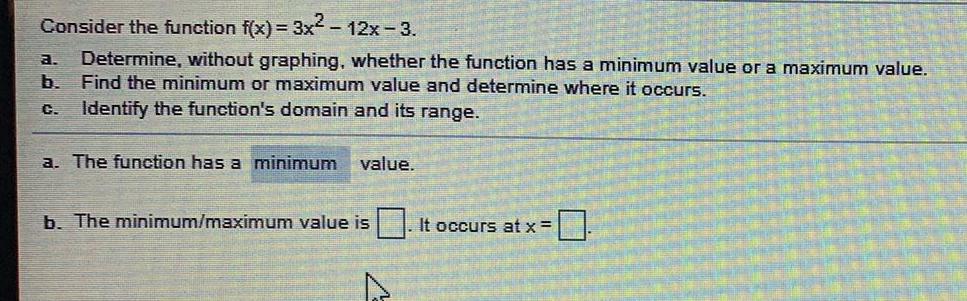
Basic MathConsider the function f(x) = 3x² - 12x-3.
a. Determine, without graphing, whether the function has a minimum value or a maximum value.
b. Find the minimum or maximum value and determine where it occurs.
C. Identify the function's domain and its range.

Math
ProbabilityIn a large population, 54 % of the people have been vaccinated. If 4 people are randomly selected,
what is the probability that AT LEAST ONE of them has been vaccinated?
Give your answer as a decimal (to at least 3 places) or fraction.

Math
StatisticsA mean average of 60 on 7 exams is needed to pass a course. On her first 6 exams, Sheryl received grades of 48, 74, 76, 61, 70 and 78.
What grade must she receive on her last exam to pass the course?
An average of 70 is needed to get a C in the course. Is it possible for Sheryl to get a C?
If her lowest grade of the exams already taken is to be dropped, what grade must she receive on her last exam to pass the course?

Math
CircleConsider a circle whose equation is x² + y² =2x-8-0. Which statements are true? Select three options.
The radius of the circle is 3 units.
The center of the circle lies on the x-axis.
The center of the circle lies on the y-axis.
The standard form of the equation is (x - 1)² + y² = 3.
The radius of this circle is the same as the radius of the circle whose equation is x² + y² = 9,

Math
Mathematical ReasoningSolve the equation 45x³ +69x2 - 13x-5 = 0 given thaT -5/3 is a zero of f(x) = 45x³ +69x² - 13x-5.

Math
StatisticsRoger sells fire trucks and dolls to a toy store. He sells each fire truck for $15 and each doll for $10. Roger wants to sell at least 25 toys and needs to earn at least $300 to cover his costs.
If each fire truck takes 50 minutes to make and each doll takes 45 minutes to make, how many fire trucks and dolls should Roger make to minimize the time spent making the toys.
A. Roger should make 15 fire trucks and 10 dolls in order to minimize the time spent making toys.
B. Roger should make 0 fire trucks and 25 dolls in order to minimize the time spent making toys.
C. Roger should make 10 fire trucks and 15 dolls in order to minimize the time spent making toys.
D. Roger should make 30 fire trucks and 0 dolls in order to minimize the time spent making toys.

Math
Sequences & SeriesGiven the following geometric sequence, find the common ratio.
(0.45, 0.9, 1.8,...)
2
0.45
0.9
1|2

Math
ProbabilityA card is picked from a standard deck of 52 cards. Determine the odds against and the odds in favor of selecting a black face card (king, queen, or jack).
The odds against selecting a black face card are:0
The odds in favor of selecting a black face card are


Math
Sets and RelationsSolve the equation x3-13x² +47x-35= 0 given that 1 is a zero of f(x) = x3 - 13x² + 47x - 35.

Math
Sequences & SeriesFor the following geometric sequence find the recursive formula and the 5th term in the sequence. In
your final answer, include all of your work.
{-4, 12, -36,...}

Math
Basic MathUse synthetic division to divide f(x) = x3 - 2x2 - 23x+60 by x-4. Use the result to find all zeros of f.
(x3 - 2x² - 23x +60) = (x-4)= ?
Math
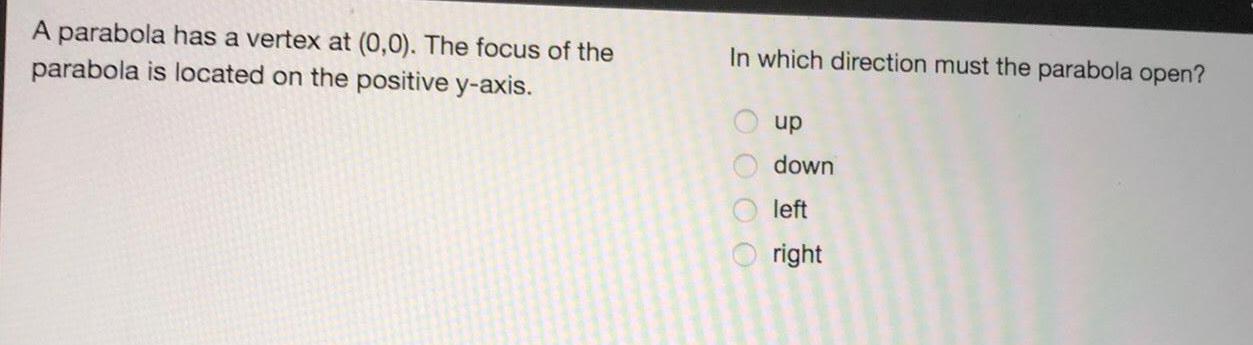
ParabolaA parabola has a vertex at (0,0). The focus of the parabola is located on the positive y-axis. In which direction must the parabola open?
up
down
left
right

Math
Basic MathOn the first day of spring, an entire field of flowering trees blossoms. The population of locusts consuming these flowers rapidly increases as the trees blossom.
The relationship between the elapsed time t, in days, since the beginning of spring, and the number of locusts, L(t), is modeled by the following function:
L(t)= 990 (1.47) ^t/4.8
Complete the following sentence about the rate of change in the locust population.
The population of locusts gains 47% of its size every ____ days.

Math
Basic MathAt the beginning of an experiment, there are 400 grams of contaminants. Each hour, three-fourths of the contaminants are filtered out.
A. Formulate a recursive sequence modeling the number of grams after n hours.
B. Use the model to calculate the amount of contaminants after the third hour of the experiment.

Math
Permutations and CombinationsSuppose a designer has a palette of 16 colors to work with, and wants to design a flag with 3 vertical stripes, all of different colors. How many possible flags can be created?

Math
Sequences & SeriesFor the following geometric sequence find the explicit formula: (-1, 3, -9, ...).
an-3-an-1 where a=-1
an = (-3) -1
an-3 an-1 where a 1
an=-1-(-3) -1

Math
Basic MathA cooler at a picnic contains 100 cans of soda covered by ice. There are 15 cans of cola, 33 cans of orange soda, 21 cans of ginger ale, and 31 cans of root beer. The cans are all the same size and shape. If one can is selected at random from the cooler, determine the probability that the soda selected is root beer.

Math
ProbabilityAccording to a study, 84% of K-12 schools or districts in a country use digital content such as ebooks, audio books, and digital textbooks. Of these 84%, 13 out of 20 use digital content as part of their curriculum. Find the probability that a randomly selected school or district uses digital content and uses it as part of their curriculum.

Math
Basic MathWhat is the probability of getting either a king or a queen when drawing a single card from a deck of 52 cards?
What is the probability that the card is either a king or a queen?

Math
ParabolaWhich equation represents the circle described?
The radius is 2 units.
The center is the same as the center of a circle whose equation is ²2+2-8x-6y + 24 = 0.
(x+4)2 + (y + 3)² = 2
(x-4)2+(y-3)²=2
(x-4)2+(y-3)² =2²
(x+42 + (y + 3)² = 2²
Math
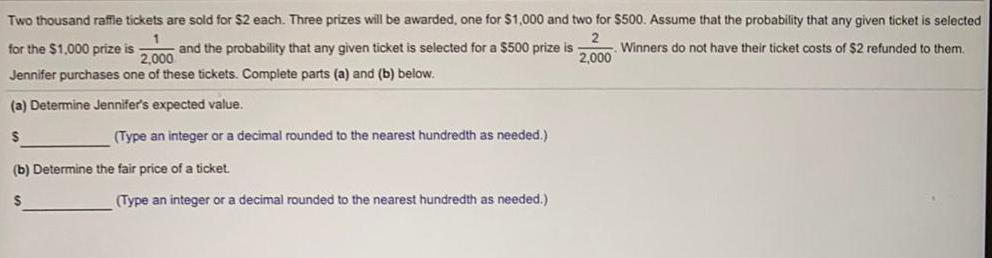
ProbabilityTwo thousand raffle tickets are sold for $2 each. Three prizes will be awarded, one for $1,000 and two for $500. Assume that the probability that any given ticket is selected 1 for the $1,000 prize is and the probability that any given ticket is selected for a $500 prize is 1/2,000 Jennifer purchases one of these tickets. Complete parts (a) and (b) below. 2/2,000 Winners do not have their ticket costs of $2 refunded to them.
(a) Determine Jennifer's expected value. (Type an integer or a decimal rounded to the nearest hundredth as needed.).
(b) Determine the fair price of a ticket. (Type an integer or a decimal rounded to the nearest hundredth as needed.)

Math
Basic MathWhich is true regarding secants and chords?
Chords intersect the perimeter of a circle at two points. Secants intersect the perimeter of a circle once.
Chords intersect the perimeter of a circle at one point. Secants intersect the perimeter of a circle twice.
Chords and secants intersect the perimeter of a circle twice. Chords are segments entirely within a circle, while secants are lines or rays that extend through a circle.
Chords and secants intersect the perimeter of a circle twice. Chords are lines or rays that extend through a circle, while secants are segments entirely within a circle.

Math
ProbabilityThe owner of an antique store estimates that there is a 40% chance she will make $2400 when she sells an antique china cabinet, a 15% chance she will make $1500 when she sells the cabinet, and a 45% chance she will break even when she sells the cabinet. Determine the expected gain or loss for the store.

Math
Basic MathA population of butterflies grow in such a way that each generation is simply 1.5 times the previous generation. There were 350 butterflies in the first generation, how many will there be by the 19th generation?

Math
CircleIn the diagram, the length of the external portion of the
secant segment PN is
The length of the entire secant segment LN is
The value of x is

Math
Quadratic equationsUse the Rational Zero Theorem to list all possible rational zeros for the given function.
f(x) = 5x4 +4x³-12x² - 4x-10
Choose the answer below that lists all possible rational zeros.
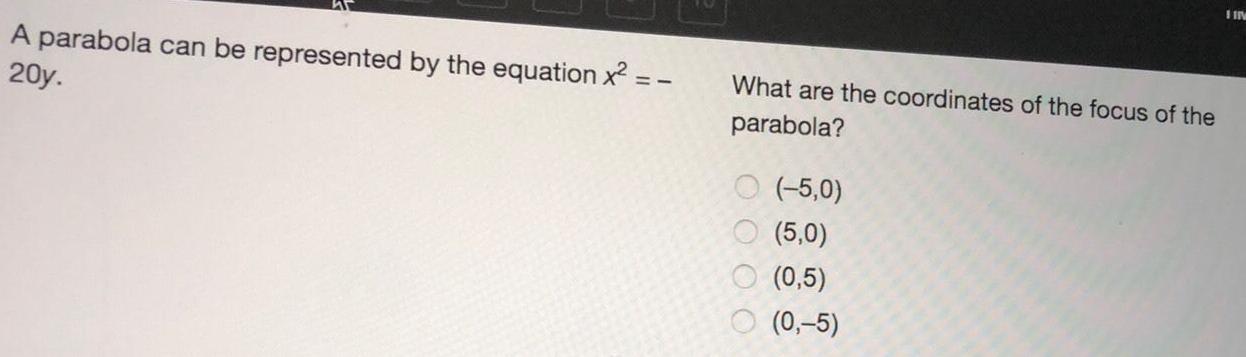
Math
ParabolaA parabola can be represented by the equation x² = - 20y.
What are the coordinates of the focus of the parabola?
(-5,0)
(5,0)
(0,5)
(0,-5)


Math
Basic MathName the set of numbers to which √25 does NOT belong.
N = natural numbers Q = rational numbers
W = whole numbers I = irrational numbers
Z = integers
Enter a, b, c, d, or e.
a. only Z
c. only Q
b. only I
d. both Z and Q.
e. both I and W
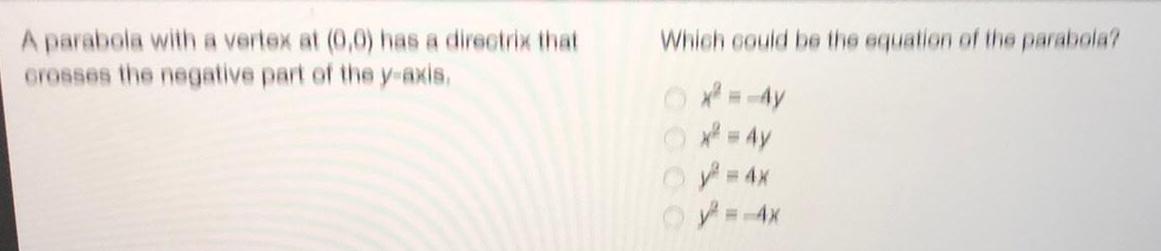
Math
ParabolaA parabola with a vertex at (0,0) has a directrix that crosses the negative part of the y-axis.
Which could be the equation of the parabola?
x^2 = -4y
x² = 4y
y² = 4x
y=-4x
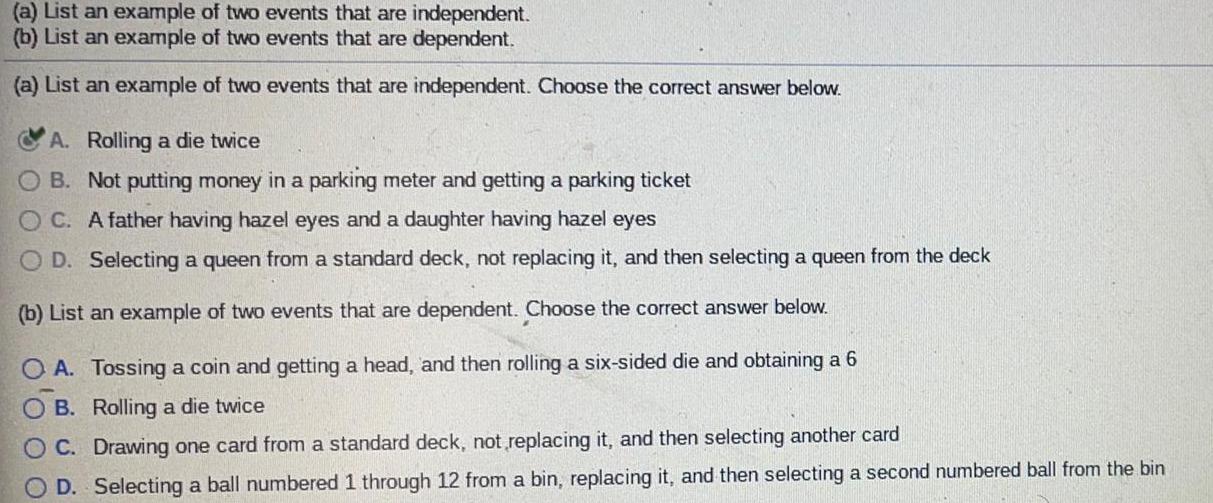
Math
Probability(a) List an example of two events that are independent.
(b) List an example of two events that are dependent.
(a) List an example of two events that are independent. Choose the correct answer below.
A. Rolling a die twice
B. Not putting money in a parking meter and getting a parking ticket
C. A father having hazel eyes and a daughter having hazel eyes
D. Selecting a queen from a standard deck, not replacing it, and then selecting a queen from the deck
(b) List an example of two events that are dependent. Choose the correct answer below.
A. Tossing a coin and getting a head, and then rolling a six-sided die and obtaining a 6
B. Rolling a die twice
C. Drawing one card from a standard deck, not replacing it, and then selecting another card
D. Selecting a ball numbered 1 through 12 from a bin, replacing it, and then selecting a second numbered ball from the bin

Math
Basic MathAccording to a study, 81% of K-12 schools or districts in a country use digital content such as ebooks, audio books, and digital textbooks. Of these 81%, 6 out of 10 use digital content as part of their curriculum. Find the probability that a randomly selected school or district uses digital content and uses it as part of their curriculum.
The probability that a randomly selected school or district uses digital content and uses it as part of their curriculum is (Round to three decimal places as needed.)

Math
Basic MathUse the given equation, which expresses price p as a function of demand x, to find a function f(p) that expresses demand x as a function of price p. Give the domain of f(p).
p=36-0.5x², 0≤x≤ √72
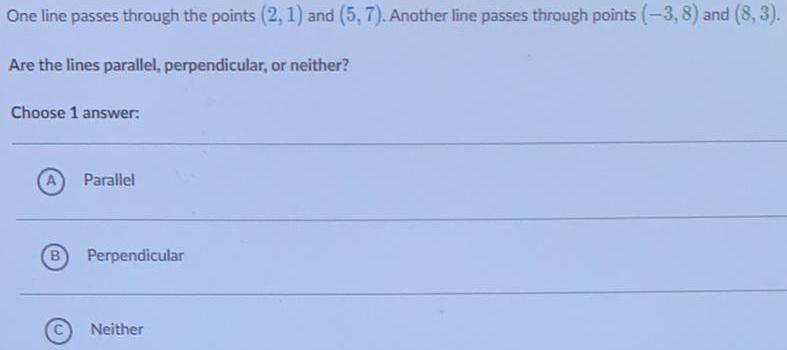
Math
Straight linesOne line passes through the points (2, 1) and (5, 7). Another line passes through points (-3, 8) and (8,3). Are the lines parallel, perpendicular, or neither?
Choose 1 answer:
A. Parallel
B. Perpendicular
C. Neither
![Which of the following illustrates the associative property of multiplication?
Enter a, b, c, d, or e.
(ab + cd) (efg) =
a. abefg+cdefg
c. [(ab + cd)e]fg
b. (cd + ab)efg
d. (abe + cde)fg
e. (egf) (ab + cd)](https://media.kunduz.com/media/sug-question/raw/52317437-1658406142.7913015.jpeg?w=256)
Math
Basic MathWhich of the following illustrates the associative property of multiplication?
Enter a, b, c, d, or e.
(ab + cd) (efg) =
a. abefg+cdefg
c. [(ab + cd)e]fg
b. (cd + ab)efg
d. (abe + cde)fg
e. (egf) (ab + cd)
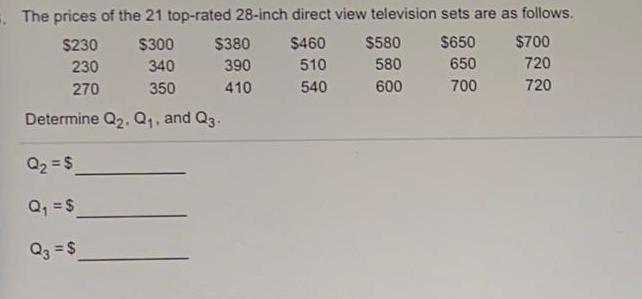
Math
StatisticsThe prices of the 21 top-rated 28-inch direct view television sets are as follows.
$300 $380 $460 $580 $650 340 390 510 580 650 350 410 540 600 700
Determine Q₂, Q₁, and Q3.
Q₂ = $
Q₁ = $
Q3 = $

Math
ProbabilitySuppose you reach into your mailbox that contains 8 pieces of junk mail, 4 letters, and 1 magazine. Assuming you can't feel the difference between the types of mail, what is the probability that you select either a letter or the magazine? Enter your answer as a fraction.

Math
ProbabilityBased on his past baseball history, Kurt has a(n) 16% chance of reaching first base safely, a(n) 8% chance of hitting a double, a(n) 5% chance of hitting a triple, a(n) 5% chance of hitting a home run, and a(n) 66% chance of making an out at his next at bat. Determine Kurt's expected number of bases for his next at bat.

Math
Sets and RelationsFor the given data:
1; 9; 15; 22; 23; 24; 24; 25; 25; 26; 27; 28; 29; 37; 45; 50
Determine the Quartiles, Q1, Q2 and Q3 of the data:
Q1:
Q2:
Q3:

Math
ProbabilitySuppose that 52% of students in a college have a smart phone. If you select three students at random, what is the probability that all three have a smart phone?

Math
Basic MathYou own 16 CDs. You want to randomly arrange 6 of them in a CD rack. What is the probability that
the rack ends up in alphabetical order?
The probability that the CDs are in alphabetical order is

Math
ProbabilityConsider a collection of envelopes consisting of 1 red envelope, 2 blue envelopes, 2 green envelopes, and 3 yellow envelopes. If two envelopes are selected at random, with replacement, determine the probability that both are blue envelopes.

Math
Basic MathA total of 15 basketballs, including 4 Brand A, 6 Brand B, and 5 other brand-name balls, are on a basketball court. Barry closes his eyes and arbitrarily picks up a ball from the court. Determine the probability that the ball selected is not a Brand B ball. The probability that the ball is not a Brand B is

Math
ProbabilityNatasha buys a bag of cookies that contains 8 chocolate chip cookies, 9 peanut butter cookies, 5 sugar cookies and 9 oatmeal raisin cookies. What is the probability that Natasha randomly selects a chocolate chip cookie from the bag, eats it, then randomly selects another chocolate chip cookie? Express your answer as a reduced fraction.
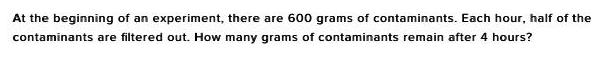
Math
Basic MathAt the beginning of an experiment, there are 600 grams of contaminants. Each hour, half of the contaminants are filtered out. How many grams of contaminants remain after 4 hours?

Math
Basic MathA pole is standing in a small lake. If one- sixth of the length of the pole is in the sand at the bottom of the lake, 25 ft are in the water, and two-thirds of the total length is in the air above the water, what is the length of the pole?

Math
Basic MathA Ferris wheel has a diameter of 42 feet. It rotates 3 times per minute. Approximately how far will a passenger travel during a 5-minute ride?
132 feet
659 feet
1,978 feet
3,956 feet