Math Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Math
Basic MathFor a moving object, the force acting on the object varies directly with the object's acceleration. When a force of 10 N acts on a certain object, the acceleration of the object is 5 m/s². If the force is changed to 18 N, what will be the acceleration of the object?

Math
Basic MathSimplify the expression
5x³ -6x²-8x/6x² - 15x + 6
and give your answer in the form of
f(x)/g(x).
Your answer for the function f(x) is:
Your answer for the function g(x) is:

Math
Application of derivativesSuppose a hiker finds himself in a forest 3 miles from the nearest point on a straight road. He wants to walk to his car which is parked 10 miles down the road. He can walk 4 mph along the road, but only 2 miles per hour through the forest. Toward what point, in miles, on the road should he walk in order to reach his car in the least time? Note: Round to the nearest thousandth.

Math
Basic MathSuppose you had $6.00 to buy bananas and apples. Bananas cost $0.49 per pound and apples cost $0.34 per pound. Write a linear equation that represents the different amounts of fruit you could buy
49x +34y = 300
49x + 34y = 600
None of the other answers are correct
49x - 34y = 600
7x + 17y=300
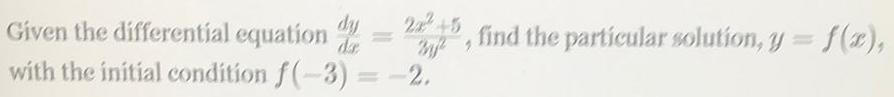
Math
Differential equationsGiven the differential equation dy/dx = 2x^2+5/3y^2, find the particular solution, y = f(x), with the initial condition f(-3) = -2.

Math
Quadratic equationsSkylar repairs washing machines. Her revenue, in dollars, can be modeled by the equationy = 80 +24x, where x is the number of hours spent repairing microwaves. Her overhead cost, in dollars, can be modeled by the equation y=x²-100, where x is the number of hours spent repairing washing machines. After how many hours does she break even?

Math
Application of derivativesUse linear approximation, i.e. the tangent line, to approximate 1/0.103 as follows: Let f(x) = 1/x and find the equation of the tangent line to f(x) at a "nice" point near 0.103. Then use this to approximate 1/0.103.

Math
Basic Math(a) A star is 5.37 light-years from Earth. If 1 light-year is about 5.9 trillion miles, how many miles is the star from Earth?
The star is about miles from Earth.
(Simplify your answer. Use scientific notation.)
(b) The mean distance from Earth to the Sun is 93,000,000 miles. What is the parallax of this star?
The parallax of the star is about
(Simplify your answer. Round to six decimal places as needed.)

Math
Mathematical ReasoningOlive bought a candle for her grandmother. She wants to mail it to her, but she only has $3. It costs $3 to mail a package with the volume of 150 in³. If the candle she bought for her grandma has a diameter of 6 inches and a height of 5 inches, will she have enough money to mail the package? Show your work in the box below to justify your answer.

Math
Straight linesThe equations of three lines are given below.
Line 1: 10x-4y=-6
Line 2: y=-2/5x+8
Line 3: 5y=-2x+6
For each pair of lines, determine whether they are parallel, perpendicula
Line 1 and Line 2: Parallel Perpendicular Neither
Line 1 and Line 3: Parallel Perpendicular Neither
Line 2 and Line 3: Parallel Perpendicular Neither

Math
Solution of trianglesPat needs to determine the height of a tree before cutting it down to be sure that it will not fall on a nearby fence. The angle of elevation of the tree from one position on a flat path from the tree is H=40°, and from a second position L = 50 feet farther along this path it is B = 30°. What is the height of the tree?
The height of the tree is approximately ft.
(Do not round until the final answer. Then round to the nearest tenth as needed.)
Math
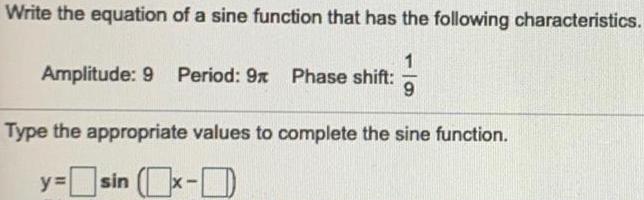
TrigonometryWrite the equation of a sine function that has the following characteristics.
Amplitude: 9 Period: 9π Phase shift: 1/9
Type the appropriate values to complete the sine function.
y=sin(x-)

Math
Basic Math4. Brady deposited $600 into a new savings account that earns 2.5% simple interest. If Brady makes no other deposits or withdrawals, how much interest will the account have earned after 5 years?
A $15
B $70
C $75
D $125

Math
Basic MathThe classrooms at Lincoln Middle School are painted every summer. If 7 gallons of paint are needed to paint 4 classrooms, how many gallons of paint are needed to paint 16 classrooms?
20 gallons
24 gallons
32 gallons
28 gallons

Math
Basic MathSurface area is:
a. the amount of matter contained in a three-dimensional object.
b. the area covering the surfaces of a three-dimensional object.
C. the amount of space occupied by a three-dimensional object.
d. the area covered by a two-dimensional object.

Math
TrigonometryA triangular plot of land has one side along a straight road measuring 289 feet. A second side makes a 62° angle with the road, and the third side makes a 56° angle with the road. How long are the other two sides?
The longer side of the triangular plot is feet. The shorter side of the triangular plot is feet.
(Round to the nearest hundredth as needed.)

Math
CircleThe equation x² + y² - 4x + 2y = b describes a circle.
Part A
Determine the y-coordinate of the center of the circle.
The y coordinate of the center is
Part B
The radius of the circle is 7 units. What is the value of bin the equation?
The value of bis

Math
Basic MathA local bank offers an investment option with a simple interest rate of 3.60% per annum. If you invest
$3200.00, how much interest will you earn in 7 years?
a. $967.68
b. $806.40
c. $791.73
d. $645.12



Math
Basic MathDecide whether the sampling method could result in a biased sample. Explain your reasoning. A representative of a mall surveys every fifth person walking into an electronics store to ask if they would like there to be a new store that sells audio equipment in the mall.

Math
Mathematical ReasoningThe slope of a ramp leading into a grocery store is 1:6 What is the angle of elevation of the ramp?
Hint: you might have to use trigonometry
a. 10.5°
b. 80.5°
c. 9.5°
d. 64.4°

Math
ProbabilityPeter Elzinga is a Dutch competitive archer who was ranked number 1 in
the world in 2004.
The probability that he makes a bullseye (i.e. a 10 point shot) on any given
shot is 0.95.
Assuming that the probability of making a bullseye on a given arrow is
independent of results on other arrows, what is the probability that Peter
Elzinga will make two bullseyes in a row followed by missing the bullseye on
the third shot (i.e., the probability of making a bullseye on the first and
second shots and something other than a bullseye on the third shot)?
Note: Round to the nearest thousandth if necessary.

Math
ProbabilitySuppose that a recent poll found that 64% of adults believe that the overall state of moral values is poor. Complete parts (a) through (c).
(a) For 250 randomly selected adults, compute the mean and standard deviation of the random variable X, the number of adults who believe that the overall state of moral values is poor.
The mean of X is (Round to the nearest whole number as needed.)
The standard deviation of X is. (Round to the nearest tenth as needed.)
(b) Interpret the mean. Choose the correct answer below.
A. For every 250 adults, the mean is the minimum number of them that would be expected to believe that the overall state of moral values is poor.
B. For every 250 adults, the mean is the range that would be expected to believe that the overall state of moral values is poor.
C. For every 250 adults, the mean is the number of them that would be expected to believe that the overall state of moral values is poor.
D. For every 160 adults, the mean is the maximum number of them that would be expected to believe that the overall state of moral values is poor.
(c) Would it be unusual if 148 of the 250 adults surveyed believe that the overall state of moral values is poor?
Yes
No

Math
Basic MathSolve this problem by using a two order system.
A man invests $5,200, part at 4% and the balance at 3%. If his total income for the two investments is $194, how much money did he invest at each rate?
$ at 4% and $ at 3%

Math
Basic MathTony invested his savings in two investment funds. The $6000 that he invested in Fund A returned a 3% profit. The amount that he invested in Fund B returned a 10% profit. How much did he invest in Fund B, if both funds together returned a 7% profit?
Amount invested in Fund B: $

Math
Basic MathMcKenna plans on attending a four-year university that costs $16,000 per year.
Her parents have agreed to contribute $2,000 each year.
Her grandparents have a college savings account that will be worth $30,900 when she graduates high school.
How much more money will she need in scholarships, loans, or work programs to attend this university for four years?
A $16,900
B $32,900
C $31,100
D $25,100

Math
Basic Math(a) Complete the square by writing ² - 16-11 in the form (x-h)² + k. Note: the numbers hand k can be positive or negative.

Math
Application of derivativesSuppose h" is continuous at x = 2.h' (2) = 0, and h" (2) < 0.
What can you say about the behavior of h at x = 2?
Inflection point
Inflection point at a horizontal tangent
Relative (local) minimum
Relative (local) maximum

Math
Basic MathDanielle and her family are discussing how to pay for her college education. The cost of tuition at the college that Danielle wants to attend is $12,000 per year. Danielle's parents will pay 75% of the tuition cost every year, and she will pay the rest. Danielle has one year to save enough money to attend her first year of college.
What is the minimum amount of money she should save every month in order to reach her goal?
A $3,000.00 B $750.00
C $40.00 D $250.00

Math
Basic MathCharles's pay varies directly with the number of words he writes for Two Cities Magazine. The first story he wrote was 4,929 words and he was paid $345.03. How much will he be paid for his next story, which is 3,825 words?
A $110.40
B $267.75
C $319.97
D $546.43

Math
FunctionsA chemist weighs samples obtained from a production run. The weights of the samples are 11 g, 10 g, 6 g. 11 g. 15 g. 13 g. 14 g, 12 g. 13 g. 12 g, 14 g, and 18 g. find the outlier(s) if there are
any. Describe how any outlier affects the mean and the standard deviation.
Q1-1.5(IQR)
Q3+1.5(IQR)

Math
Basic MathLupita deposited $5,000 into a savings account that earns 2% interest compounded annually. Rounded to the nearest cent, how much interest will Lupita have earned after 48 months?
The answer is $
Math
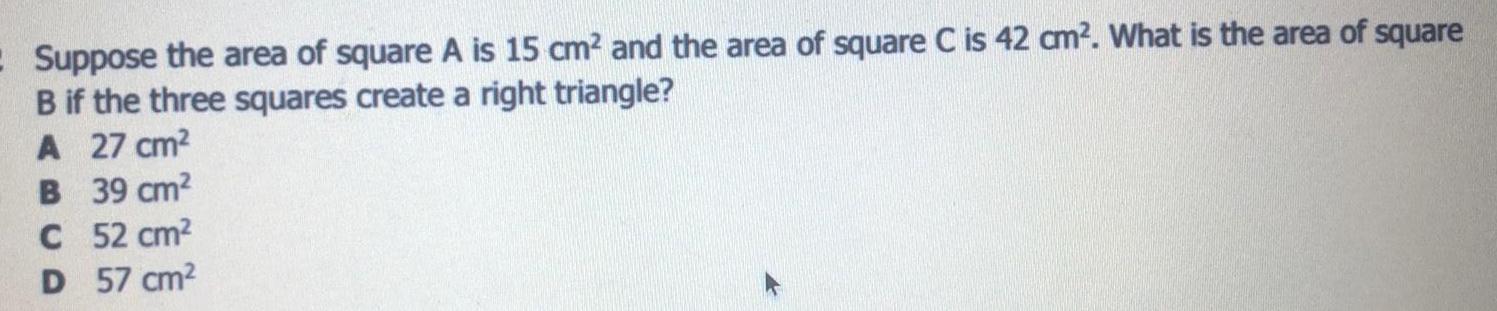
AreaSuppose the area of square A is 15 cm² and the area of square C is 42 cm². What is the area of square
B if the three squares create a right triangle?
A 27 cm²
B 39 cm²
C 52 cm²
D 57 cm²

Math
Basic MathThe mass of a textbook is approximately 0.00165 metric ton. How is this number written in
scientific notation?
F 165 x 10^-5
G 1.65 x 10^-3
H 16.5 x 10^-4
J 0.165 x 10^-2

Math
Basic MathJohn is 5 years older than Mary. In 10 years, twice John's age decreased by Mary's age Is 35, and John's age will be twice Mary's current age. Find their ages now.
If x Is Mary's age now and yis John's age now, which system of equations could not be used to solve the problem?
y=x+ 5 and 2(y + 10) = x
y=x+ 5 and 2(y+10)-(x+10) = 35
y=x+5 and y + 10 = 2x

Math
Basic MathFrank earns $40,000 one year and receives a 6% raise in salary. What is his new salary?
Frank's new salary is $. (Simplify your answer.)

Math
ProbabilityA trade magazine routinely checks the drive-through service times of fast-food restaurants. A 90% confidence interval that results from examining 595 customers in one fast-food chain's drive-through has a lower bound of 159.3 seconds and an upper bound of 162.9 seconds. What does this mean?
Choose the correct answer below.
A. One can be % confident that the mean drive-through service time of this fast-food chain is seconds.
B. The mean drive-through service time of this fast-food chain is seconds % of the time.
C. There is a 90% probability that the mean drive-through service time of this fast-food chain is between seconds and seconds.
D. One can be 90% confident that the mean drive-through service time of this fast-food chain is between seconds and seconds.
![Let f(x) = (3x - 1)² (3x - 7)² on [1,3]. Answer the following.
(a) Find all critical numbers of f.
(b) Find the intervals on which f is increasing.
(c) Find absolute extreme value of f.](https://media.kunduz.com/media/sug-question/raw/46196864-1658295031.8314972.jpeg?w=256)
Math
Application of derivativesLet f(x) = (3x - 1)² (3x - 7)² on [1,3]. Answer the following.
(a) Find all critical numbers of f.
(b) Find the intervals on which f is increasing.
(c) Find absolute extreme value of f.

Math
Basic MathJames is investing $15,000 in the bank. The investment has an interest rate of 6% compounded monthly. After ten years, how much will James have made?
The answer is $
Make sure to round correctly. Think MONEY.

Math
Basic MathA kitchen is shaped like a rectangle with dimensions of 11(1/2) ft by 9(1/2) ft. The floor of the room is made of square tiles with a side length of 1/2 ft. What is the number of tiles that will cover the kitchen floor?

Math
Basic MathA guy wire that is used to support a pole is attached at a height of 55 ft and at an angle of 62.1° above the ground. How far from the base of the pole is the guy wire attached to the ground?
a. 29.12 ft
b. 48.61 ft
c. 117.54 ft
d. 62.23 ft

Math
Basic MathA principal is ordering pizza for a school pizza party. He knows that 9 pizzas
will feed 25 students. If there are 300 students in the school, how many
pizzas will he need to order?
108 pizzas
102 pizzas
105 pizzas
99 pizzas

Math
Basic MathAhmad and his wife are each starting a saving plan. Ahmad will initially set aside $650 and then add $135 every month to the savings. The amount A (in dollars) saved this way is given by the function A = 650+ 135N, where N is the number of months he has been saving.
His wife will not set an initial amount aside but will add $495 to the savings every month. The amount B (in dollars) saved using this plan is given by the function B=495N.
Let I be total amount (in dollars) saved using both plans combined. Write an equation relating I to N. Simplify your answer as much as possible.

Math
Application of derivativesA toy manufacturing company's monthly profit in its first two months of operation is given by the profit function
P(x) = x³ -6x2 +9x+6, where is the number of toys sold and P(x) is In thousands of dollars (for example, if P(x) = 3, then the company's profit is $3000).
What is the company's maximum profit during the first two months?

Math
Basic MathIn a given year, residents of a country spent approximately $50.4 billion on their pets. Of this amount, $18.9 billion was for veterinarian bills. What percent of the total was spent on veterinary care? About % of the total was spent on veterinary care.

Math
Basic MathState the order and type of each transformation of the graph of the function
f(x) = (5(x - 1))3 - 2 as compared to the graph of the base function.
right 1 unit, horizontal compression by a factor if 1/5 down 2 units
Oright 1 unit, vertical stretch by a factor if 5, down 2 units
right 1 unit, down 2 units, vertical stretch by a factor if 5
right 1 unit, down 2 units, horizontal compression by a factor if 1/5

Math
StatisticsThe shape of the distribution of the time required to get an oil change at a 10-minute oil-change facility is unknown. However, records indicate that the mean time is 11.1 minutes, and the standard deviation is 4.3 minutes. Complete parts (a) through (c) below.
Click here to view the standard normal distribution table (page 1).
Click here to view the standard normal distribution table (page 2).
(a) To compute probabilities regarding the sample mean using the normal model, what size sample would be required?
Choose the required sample size below.
O A. Any sample size could be used.
OB. The normal model cannot be used if the shape of the distribution is unknown.
C. The sample size needs to be less than 30.
D. The sample size needs to be greater than 30.
(b) What is the probability that a random sample of n = 35 oil changes results in a sample mean time less than 10 minutes?
The probability is approximately
(Round to four decimal places as needed.)
(c) Suppose the manager agrees to pay each employee a $50 bonus if they meet a certain goal. On a typical Saturday, the oil-change facility will perform 35 oil
changes between 10 A.M. and 12 P.M. Treating this as a random sample, at what mean oil-change time would there be a 10% chance of being at or below? This will
be the goal 'established by the manager.
Click to select your answer(s).

Math
StatisticsThe local Art Club has 5 members. Their ages are 19, 25, 30, 63, and 30. Find the mode, mean, and standard deviation. Make sure you label each answer.

Math
Complex numbersWrite the expression in rectangular form, x+y i, and in exponential form, reiθ
(√13-i)4
The rectangular form of the given expression is. and the exponential form of the given expression is
(Simplify your answers. Use integers or decimals for any numbers in the expressions. Round the final answer to three decimal places as needed. Round all intermediate values to four decimal
places as needed.)