Math Questions

Let f be the function defined as f(x)= 2 for x<4 f(x)= 4x-3 for x≥4 Which of the following statements is true? f is not differentiable at x = 4 because fis not defined at x = 4. f is not differentiable at x = 4 because the graph of f has a cusp at x = 4. f is not differentiable at x = 4 because the graph of f has a vertical tangent at x = 4. f is not differentiable at x = 4 because f is not continuous at x = 4,

You are going to survey a random sample of the 300 passengers on a flight from San Francisco to Tokyo. Name each sampling method described. a. Randomly generate 30 seat numbers and survey the passengers who sit there. b. Randomly select a seat position (right window, center, aisle, etc.) and survey all of the passengers sitting in those seats.

Let S be the event that a randomly chosen voter supports the president. Let W be the event that a randomly chosen voter is a woman. Identify the answer which expresses the following with correct notation: The probability that a randomly chosen voter is a woman, given that the voter supports the president. Select the correct answer below: P(WIS) P(S AND W) P(W) AND P(S) P(SW)

A youth organization collected nickels and dimes for a charity drive. By the end of the 1-day drive, the youth had collected $48.65. If there were three times as many dimes as nickels, how many of each type of coin was collected?

Assume SAT Math scores are normally distributed with a mean of 500 and standard deviation of 100. A) Find the probability that a student scores lower than 575 B) Find the probability that a student scores higher than 393.

For studying the electric current that is induced in wire rotating through a magnetic field, a piece of wire 88 cm long is cut into two pieces. One of these is bent into a circle and the other into a square. Express the total area A of the two figures as a function of the perimeter of the square. Use p for the perimeter of the square. A= (Simplify your answer. Do not factor. Type an exact answer, using as needed. Use integers or fractions for any numbers in the expression.)

Which function translates each point on the graph of y = mx + b so that the slope of the segment from the original point to the translated point is 1/2 ? t(x)=1/2x+b t(x) = m(x-2) +b+1 h(z) = mx + b g(x) = m(x-2) +b-1

On a poultry farm eggs are packed in cartons. Each carton contains 12 boxes and each box contains 15 eggs of mixed size (small, medium and large). On the farm 1 out of 9 eggs is large and the packing machine selects the eggs randomly. Find the expected number of large eggs in a carton.

A 28-year-old man pays $223 for a one-year life insurance policy with coverage of $60,000. If the probability that he will live through the year is 0.9993, what is the expected value for the insurance policy? -$181.00 $59.958.00 $42.00 -$222.84

a. Write the equation of the line that represents the linear approximation to the following function at the given point a. b. Use the linear approximation to estimate the given quantity. c. Compute the percent error in the approximation, 100.|approximation - exact|/|exact| where the exact value is given by a calculator. f(x) = 6-x² at a = 1; f(0.9)

An investment grows at 24% compounded monthly. How many years will it take to do the following? (Round your answers to one decimal place.) (a) double (b) increase by 65%

among automobiles of a certain make, 23% require service during a one-year warranty period. A dealer sells 87 of these vehicles. a.) Approximate the probability that 25 or fewer of these vehicles require repairs. b.) Approximate the probability that more than 17 vehicles require repairs.

There's one other alternative-one that takes both skill and courage: Forgoing any cradling action, grasp the cone more firmly between thumb and forefinger and extend the other fingers so that they are out of the way of the dripping from the bottom, then increase the waist-bend angle from twenty-five degrees to thirty-five degrees, and then eat the cone, allowing it to drip out of the bottom onto the ground in front of you! Experienced and thoughtful cone-eaters enjoy facing up to this kind of sudden challenge. What is the author's purpose for including this portion of "How to Eat an Ice- Cream Cone"? A. To entertain the audience with humor B. To appeal to the audience with emotion C. To inform the audience with facts D. To persuade the audience with language

Graph the function f(x) = 7(x + 2)² - 6. Plot the vertex. Then plot another point on the parabola. If you make a mistake, you can erase your parabola by selecting the second point and placing it on top of the first.

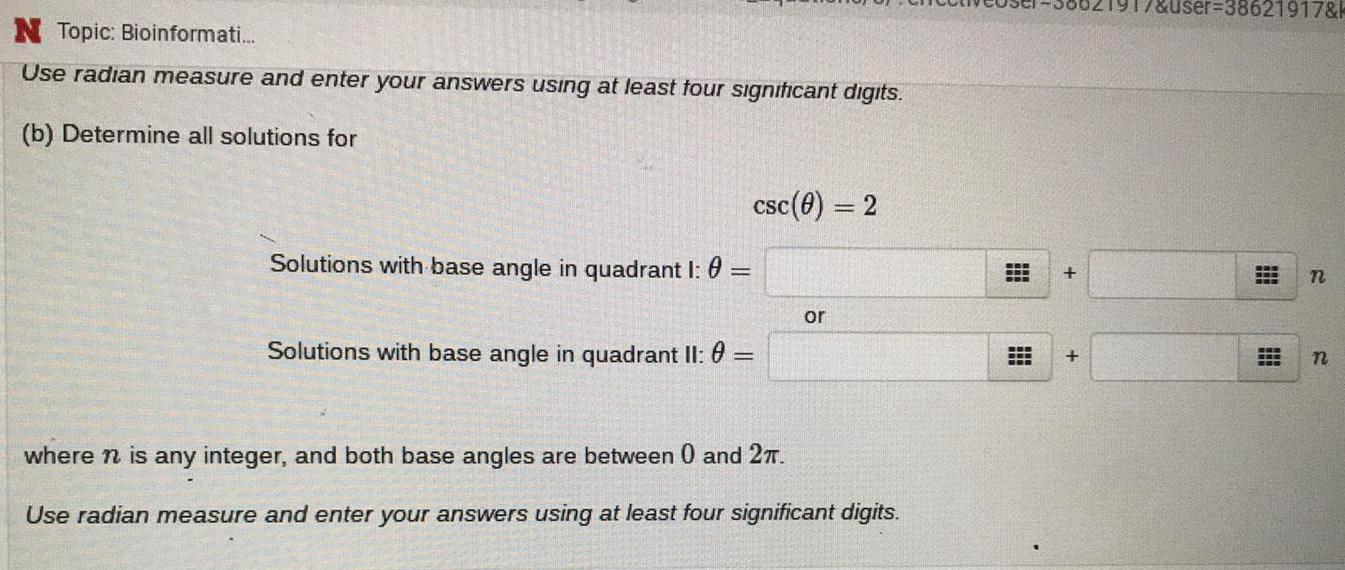
Use radian measure and enter your answers using at least four significant digits. (b) Determine all solutions for csc(θ)=2 Solutions with base angle in quadrant I: θ= Solutions with base angle in quadrant II: θ= where n is any integer, and both base angles are between 0 and 2π Use radian measure and enter your answers using at least four significant digits.

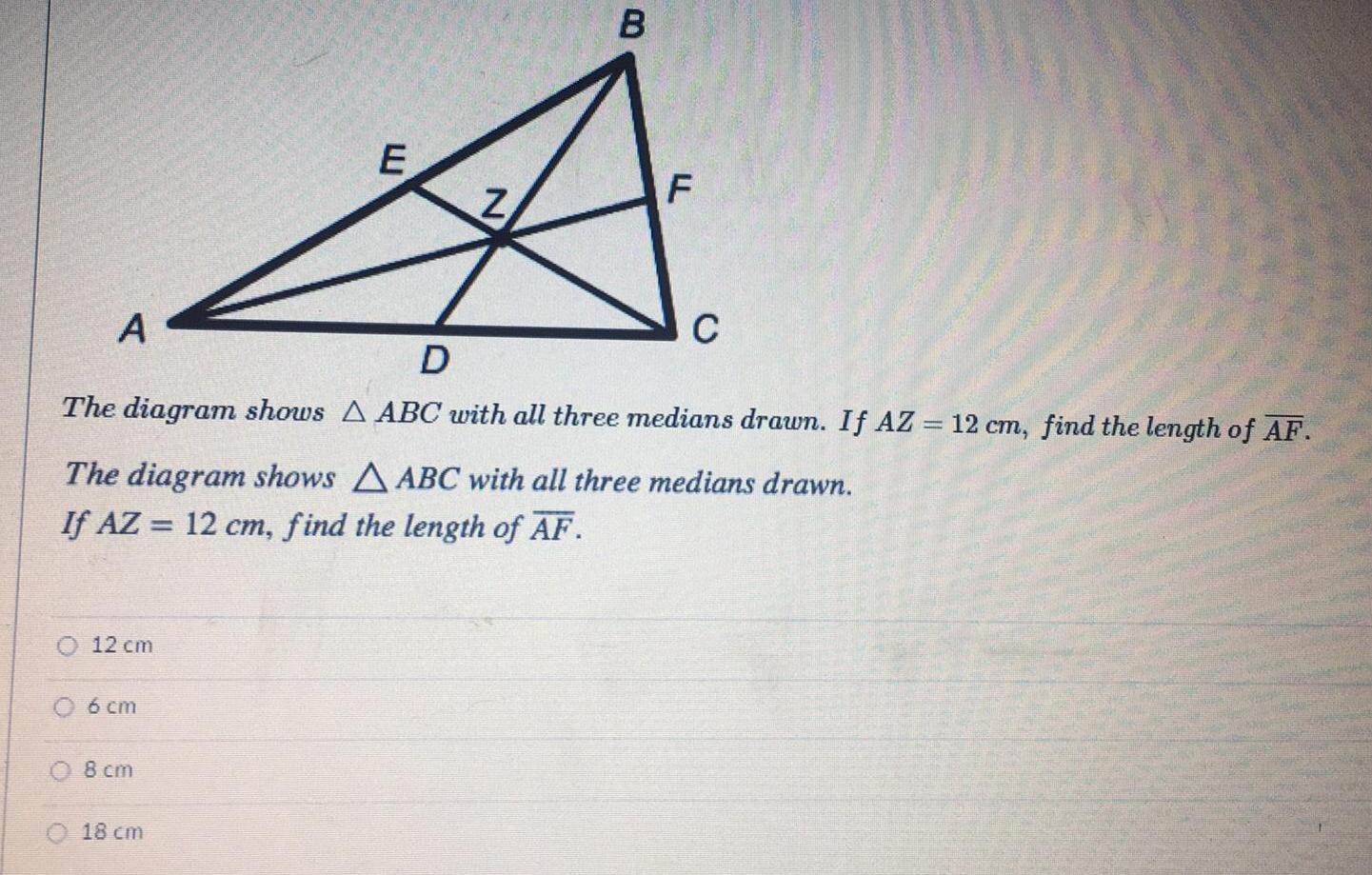
The product of two numbers is to be minimized. The second number is eight more than twice the first. Call the first number "x." a) Write an equation for the product of the numbers with respect to the first number. (4 points) b) What is their minimum product? (2 points) c) What two numbers make this minimum product? (4 points)

The diagram shows ΔABC with all three medians drawn. If ΔZ = 12 cm, find the length of AF. The diagram shows ΔABC with all three medians drawn. If AZ = 12 cm, find the length of AF. a.12 cm b. 6 cm c. 8 cm d. 18 cm

The Cartesian coordinates of a point are given. (a) (-7,7) (i) Find polar coordinates (r, θ) of the point, where r> 0 and 0 ≤ θ< 2π (r,θ) = (ii) Find polar coordinates (r, θ) of the point, where r < 0 and 0 ≤ θ< 2π (r, θ) = (b) (2,2√3) Find polar coordinates (r, 8) of the point, where r> 0 and 0 ≤ θ < 2π. (r, θ) = (ii) Find polar coordinates (r, 8) of the point, where r < 0 and 0 ≤ θ < 2π. (r, θ) =

ΔABC is reflected across the x-axis and then translated 4 units up to create ΔA'B'C. What are the coordinates of the vertices of ΔA'B'C? A. A'(-3, 3), B'(-1, 1), C'(-2, 3) B. A'(3, -3), B'(1, -1), C'(2, -3) C. A'(3, -5), B'(1, -7), C'(3, -5) D. A'(-3, 3), B'(-1, 1), C'(-2, -3)

Assume that the readings at freezing on a batch of thermometers are normally distributed with a mean of 0°C and a standard deviation of 1.00°C. A single thermometer is randomly selected and tested. Find P₁9, the 19-percentile. This is the temperature reading separating the bottom 19% from the top 81%. P19 = °C

The duration of a professor's class has a continuous uniform distribution between 50.0 minutes and 52.0 minutes. If one class is randomly selected, find the probability that the professor's class duration is between 51.2 and 51.5 minutes. P(51.2 < X < 51.5) =

The top of a 5 foot ladder, leaning against a vertical wall, is slipping down the wall at the rate of 3 feet per second. How fast is the bottom of the ladder sliding along the ground away from the wall when the bottom of the ladder is 4 feet away from the base of the wall?

You invest $2500 in an account at interest rate r, compounded continuously. Find the time required for the amount to double and triple. (Round your answers to two decimal places.) r = 0.0485 (a) double (b) triple

For the function f(x) = - 1/12x, construct and simplify the difference quotient f(x+h)-f(x)/ h The difference quotient for f(x) = - 1/12x is (Simplify your answer. Use integers or fractions for any numbers in the expression.)

The area of a square is increasing at a rate of 12 centimeters squared per second. Find the rate of change of the side of the square when it is 2 centimeters.

A bicyclist rides 24 mi against a wind and returns 24 mi with the same wind. His average speed for the return trip traveling with the wind is 8 mph faster, than his speed going out against the wind. If x represents the bicyclist's speed going out against the wind, then the total time, t required for the round trip is given by t = 24/x +24/x+8 where t is measured in hours a) Find the time required for the round trip if the cyclist rides 12 mph against the wind b) Find the time required for the round trip if the cyclist rides 24 mph against the wind

The running lanes at the Emery Sears track at Bluffton College are 1 m wide. The inside radius of lane 1 is 33 m, and the inside radius of lane 2 is 34 m. How much longer is lane 2 than lane 1 around one turn? * (25 Points) 106.814 m 103.673 m 3.142 m 4.142 m

Jessica Cardenas has a sprinkler that has several varieties of coverage. The quarter-circle sprinkler head sprays water a distance of up to 20 feet from the head. What area will be covered by the spray of the quarter-circle sprinkler head to the nearest square foot? * (25 Points) 493 ft² 314 ft² 25 ft² 31 ft²

The functions=t³-15t² +75t,0≤t≤ 5, gives the position of a body moving on a coordinate line, with s in meters and t in seconds. a. Find the body's displacement and average velocity for the given time interval. b. Find the body's speed and acceleration at the endpoints of the interval. c. When, if ever, during the interval does the body change direction? a. What is the body's displacement for the given time interval? m (Simplify your answer.) What is the average velocity for the given time interval? m/s (Simplify your answer.) b. What is the body's speed at t=0? m/s (Simplify your answer.) *****

A 95 kg basketball player jumped in the air to secure a rebound. During the last step before jumping in the air, 1,792 N of ground reaction force was applied to the basketball player over a duration of 400 ms a.What is the average net vertical force during the jump? b.What is the impulse the basketball player experienced during the jump? c. What is the momentum the basketball player experienced during the jump? d. What is the basketball player's vertical velocity at the instant of takeoff? e. How high did the basketball player's center of mass rise during his jump?

The cost of renting a space for up to 400 people is a $700 flat fee. The cost of catering a dinner for x attendees is given by C(x) = 300+ 32x. Write an equation for the total cost, T(x), of putting on a prom if these are the only two expenses.

11 Mr. Davis and Ms. Lee saved the same amount of money. Mr. Davis spent $1,140 on a television and Ms. Lee spent $580 on a stand mixer. Ms. Lee then had 9 times as much money as Mr. Davis. How much money did Mr. Davis have at first?

For every three girls taking classes at a martial arts school, there are 4 boys who are taking classes. Suppose there are 236 boys taking classes at the school. Write a proportion that could be used to predict the number of girls taking classes at the school. Use x to represent the number of girls.

The cost of reserving a particular domain name is $21 up front plus $4.49 per month. Find the cost of reserving that domain name for the following:

Given that f(x)=x²-19 and g(x) = 6x +1, find (fg)(-1/6) A. (fg)(-1/6)= (Simplify your answer.) Select the correct choice below and, if necessary, fill in the answer box to complete your choice. B. The value for (fg)(-1/6) does not exist.

a. For the function and point below, find f'(a). b. Determine an equation of the line tangent to the graph of f at (a,f(a)) for the given value of a. f(x) = 2x² +3x, a = -2

For a given input value u, the function g outputs a value v to satisfy the following equation. -12u + 3 = 8v + 1 Write a formula for g(u) in terms of u. g(u) =

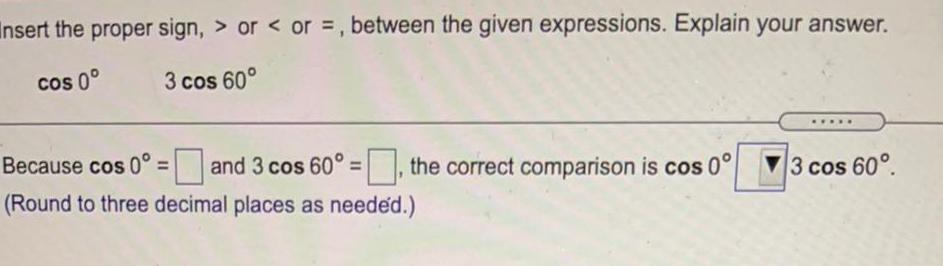
Insert the proper sign, > or < or =, between the given expressions. Explain your answer. cos 0° 3 cos 60° Because cos 0° = and 3 cos 60° =, the correct comparison is cos 0° 3 cos 60°. (Round to three decimal places as needed.)

Find the coordinates of both intercepts for the line. Express numbers in exact simplified form. -8x-3y=-23 The X intercept has the coordinates The intercept has the coordinates

A mirror should be centered on a wall. The mirror is 36 inches wide and the wall is 18 feet wide. Which equation helps determine the distance x on each side of the mirror? A) X + 3 + x = 18 B) X = 18 + 3 C) X + 36 + x = 18 D) 3 + x + 3 = 18

27) A-Plus Advertising charges a fee of $27 plust $0.10 per flyer to print and deliver flyers. Print and More charges $0.25 per flyer. For how many flyers is the cost at A-plus Advertising less than the cost at Print and More?

State if the given functions are inverses. * g(x)=2x+4 f(x) = x-4/2 A) Yes B) No

A box of chocolates contains six milk chocolates and seven dark chocolates. You randomly pick a chocolate and eat it. Then you randomly pick another piece. What is the probability that the first piece is milk chocolate and the second is dark chocolate?

Solve the equation by using the quadratic formula. 2p² = -8p+3 Select the correct answer below and, if necessary, fill in the answer box to complete your choice. A. The solution is p = (Type an exact answer, using radicals as needed. Use a comma to separate answers as needed.) B. There are no real roots.

A ferris wheel is 45 meters in diameter and boarded from a platform that is 5 meters above the ground. The six o'clock position on the ferris wheel is level with the loading platform. The wheel completes 1 full revolution in 2 minutes. The function h-f(t) gives your height in meters above the ground t minutes after the wheel begins to turn. What is the Amplitude? meters What is the Midline? y= meters What is the Period? minutes How High are you off of the ground after 1 minutes? meters

Which of the following is true about the graph of f(x) = 2 sin³(x) + 3 sin(x) + 2 on the interval [0, π]? a) f(x) has a local minimum at the point (π,7). b) f(x) has points of inflection at the points (π/4,2√2+2) and (3π/4, 2√2+2). c) f(x) is concave down on the interval (0, π). d) f(x) is concave up on the interval (0, π). e) f(x) is increasing on the interval (π/2, π).

Incline mats, or triangle mats, are offered with different levels of incline to help gymnasts learn basic moves. As the name may suggest, the ends of these mats are right triangles. If the height of the mat is 28 inches shorter than the length of the mat and the hypotenuse is 8 inches longer than the length of the mat, what is the length of the mat?

To rent a certain meeting room, a college charges a reservation fee of $14 and an additional fee of $4 per hour. The chemistry club wants to spend less than $50 on renting the room. What are the possible numbers of hours the chemistry club could rent the meeting room? Use / for the number of hours. Write your answer as an inequality solved for t.

Differentiate the function, and find the slope of the tangent line at the given value of the independent variable. f(x) = 5x + 4/x, x = -5 The derivative of the function f(x) = 5x + 4/x is The slope of the tangent line at x = -5 is

A company pays its sales people a base salary of $38,500 per annum plus a commission of 12% on all sales. Stephen, one of the company's salespeople, made sales worth $105,000 in his first year. a. Calculate the commission Stephen earned during the year. Round to the nearest cent b. Calculate the total salary Stephen earned during the year.