Math Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Math
StatisticsWhich of the following is NOT involved in the process of interpreting pictures?
Determine what type of picture it is.
Form an opinion on the quality of work.
Analyze the author's intentions.
Observe the elements of the picture.

Math
StatisticsThe average height of young adult males has a normal distribution with standard deviation of 2.4 inches. You want to estimate the mean height of students at your college or university to within one inch with 99% confidence. How many male students must you measure?

Math
Basic MathA bus traveled on a level road for 6 hours at an average speed 20 miles per hour faster than it traveled on a winding road. The time spent on the winding road was 3 hours. Find the average speed on the level road if the entire trip was 498 miles.

Math
Basic MathAfter the end of an advertising campaign, the daily sales of a product fell rapidly, with daily sales given by S=3500e-0.12x dollars, where x is the number of days from the end of the campaign.
a. What were daily sales when the campaign ended?
b. How many days passed after the campaign ended before daily sales were below half of what they were at the end of the campaign?

Math
ProbabilityAntibiotic resistance occurs when disease-causing microbes no longer respond to antibiotic drug therapy. Because such resistance is typically genetic and transferred to the next generations of microbes, it is a very serious public health problem. Gonorrhea is the second most commonly reported notifiable disease in the United States. According to the Centers for Disease Control and Prevention (CDC), 27% of gonorrhea cases tested in 2010 were resistant to at least one of the three major antibiotics commonly used to treat this sexually transmitted disease.
The CDC reported that 38% of gonorrhea cases tested in 2014 were resistant to at least one of the three major antibiotics commonly used to treat gonorrhea.
(a) In 2010, out of 10 randomly selected gonorrhea cases, what is the mean of the count of cases X showing resistance to at least one of the three major antibiotics? (Enter your answer rounded to one decimal place.)
Math
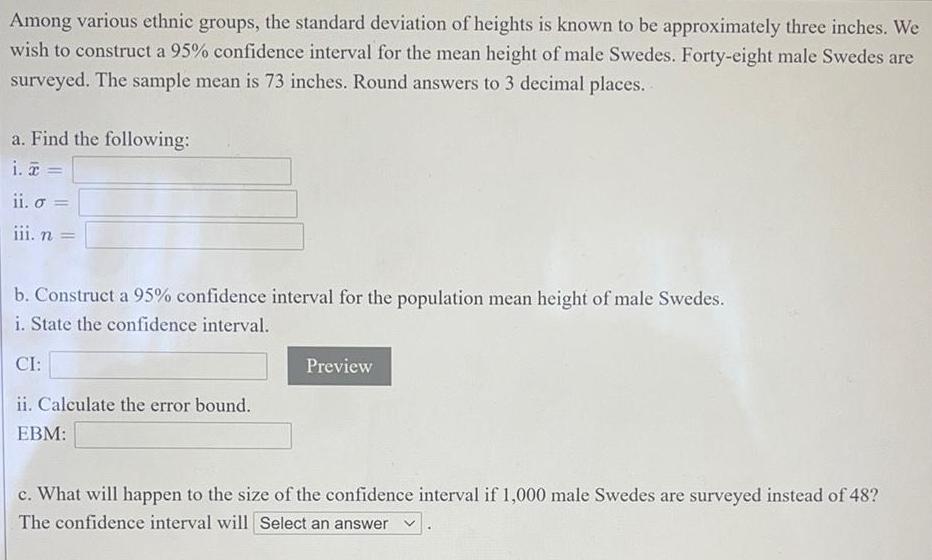
StatisticsAmong various ethnic groups, the standard deviation of heights is known to be approximately three inches. We wish to construct a 95% confidence interval for the mean height of male Swedes. Forty-eight male Swedes are surveyed. The sample mean is 73 inches. Round answers to 3 decimal places.
a. Find the following:
i. =
ii. o =
iii. n =
b. Construct a 95% confidence interval for the population mean height of male Swedes.
i. State the confidence interval.
ii. Calculate the error bound.
c. What will happen to the size of the confidence interval if 1,000 male Swedes are surveyed instead of 48?
The confidence interval will

Math
Basic Math1. Zachary's final project for a college course took a semester to write and had 95,234 words. Zachary wrote 35,295 words the first month and 19,240 words the second month.
a. Round each value to the nearest ten thousand to estimate how many words Zachary wrote during the
remaining part of the semester.

Math
Basic MathJoel sells ice cream cones at the county fair. He has to rent the equipment for $34 and spend $0.53 on ingredients for each cone. Write an inequality and solve it to represent the possible numbers of ice cream cones that he must sell at $1.10 each in order to make a profit.

Math
Basic MathMr. Harris has some money in his wallet. He pays the babysitter $12 an hour for 4 hours of babysitting. His wife gives him $10, and he puts the money in his wallet. By how much does the amount in his wallet change?

Math
Basic MathThree sisters have ages that are consecutive odd integers. The sum of the age of the youngest and three times the age of the oldest is five less than five times the middle sister's age.
(a) If x represents the age of the youngest child, then write an equation that models this scenario.
Math
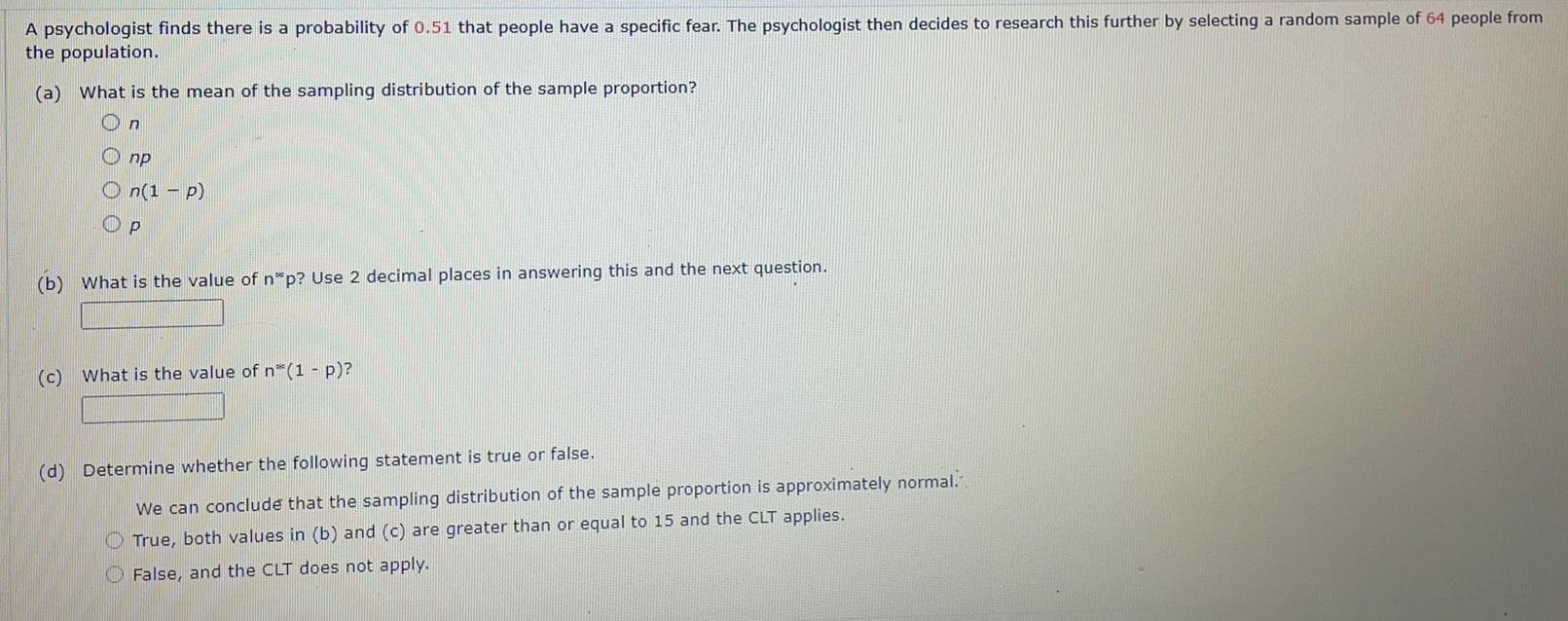
Basic MathA psychologist finds there is a probability of 0.51 that people have a specific fear. The psychologist then decides to research this further by selecting a random sample of 64 people from the population.
(a) What is the mean of the sampling distribution of the sample proportion?
n
p
n(1-P)
p
(b) What is the value of n*p? Use 2 decimal places in answering this and the next question.
(c) What is the value of n*(1 - p)?
(d) Determine whether the following statement is true or false.
We can conclude that the sampling distribution of the sample proportion is approximately normal.
True, both values in (b) and (c) are greater than or equal to 15 and the CLT applies.
False, and the CLT does not apply.

Math
Basic MathAt a concession stand, seven hot dog(s) and four hamburger(s) cost $16.00; four hot dog(s) and seven hamburger(s) cost $19.75. Find the cost of one hot dog and the cost of one hamburger.
What is the cost of one hot dog?
What is the cost of one hamburger?

Math
ProbabilityIn a test for ESP (extrasensory perception), a subject is told that cards only the experimenter can see contain either a star, a circle, a wave, or a square. As the experimenter looks at each of 20 cards in turn, the subject names the shape on the card. A
subject who is just guessing has probability 0.25 of guessing correctly on each card.
(a) The count of correct guesses in 20 cards has a binomial distribution. What is the value of n? (Enter your answer as a whole number.)
n=
What is the value of p? (Enter your answer rounded to two decimal places.)
P=

Math
LogarithmsRewrite the expression e^5 ln(x) so that no exponential or logarithmic functions are involved. The formula b^ln t = r and the basic rules of exponents will be helpful. Assume that x and y are positive.

Math
ProbabilityBlood type AB is somewhat rare in the United States (it is found in 4% of the general population). It is particularly useful for plasma transfusions because this plasma can be accepted by individuals with all blood types. The plasma is the liquid part of the blood once all cells are removed. You count the number X of AB donors who come to a fixed Red Cross location per day. This count has the Poisson distribution, with parameter being the mean number of AB donors per day.
(a) The donation center sees an average of 2.1 AB donors per day. Find the Poisson probabilities for X = 0, 1,2,3,4,5.
P(X = 0) =
P(X= 1) =
P(X=2)=
Math
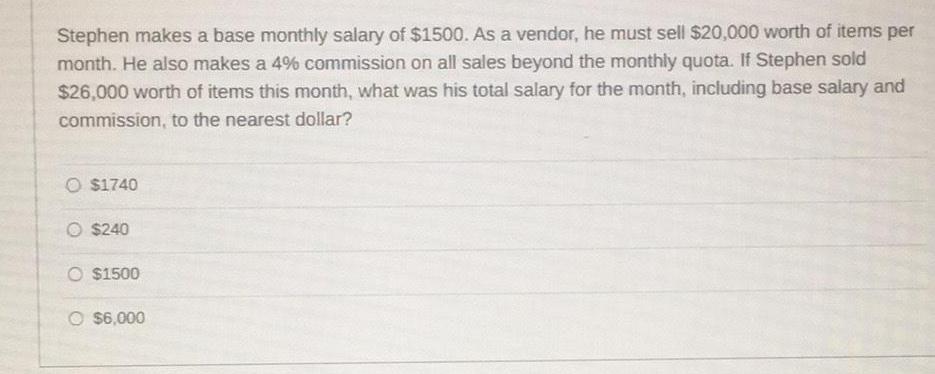
Basic MathStephen makes a base monthly salary of $1500. As a vendor, he must sell $20,000 worth of items per month. He also makes a 4% commission on all sales beyond the monthly quota. If Stephen sold
$26,000 worth of items this month, what was his total salary for the month, including base salary and commission, to the nearest dollar?
$1740
$240
$1500
$6,000


Math
ProbabilityA modified roulette wheel has 28 slots. One slot is 0, another is 00, and the others are numbered 1 through 26, respectively. You are placing a bet that the outcome is
an odd number. (In roulette, 0 and 00 are neither odd nor even.)
a. What is your probability of winning?
The probability of winning is
(Type an integer or a simplified fraction.)

Math
Basic MathNewfoundland is a large breed of dog. It weighs about 10 x 10 pounds. Write 10 × 10 using an exponent. Then find the value of the power. How many pounds does the Newfoundland weigh?

Math
AreaWally Beige has painted a rectangular mural that is 8 ft tall and 10 ft wide. He plans to paint a border of equal width all the way around the outside of the mural. To end up with a border that has an area of 144 square ft, find the width of the border.
Answer: ft
Math
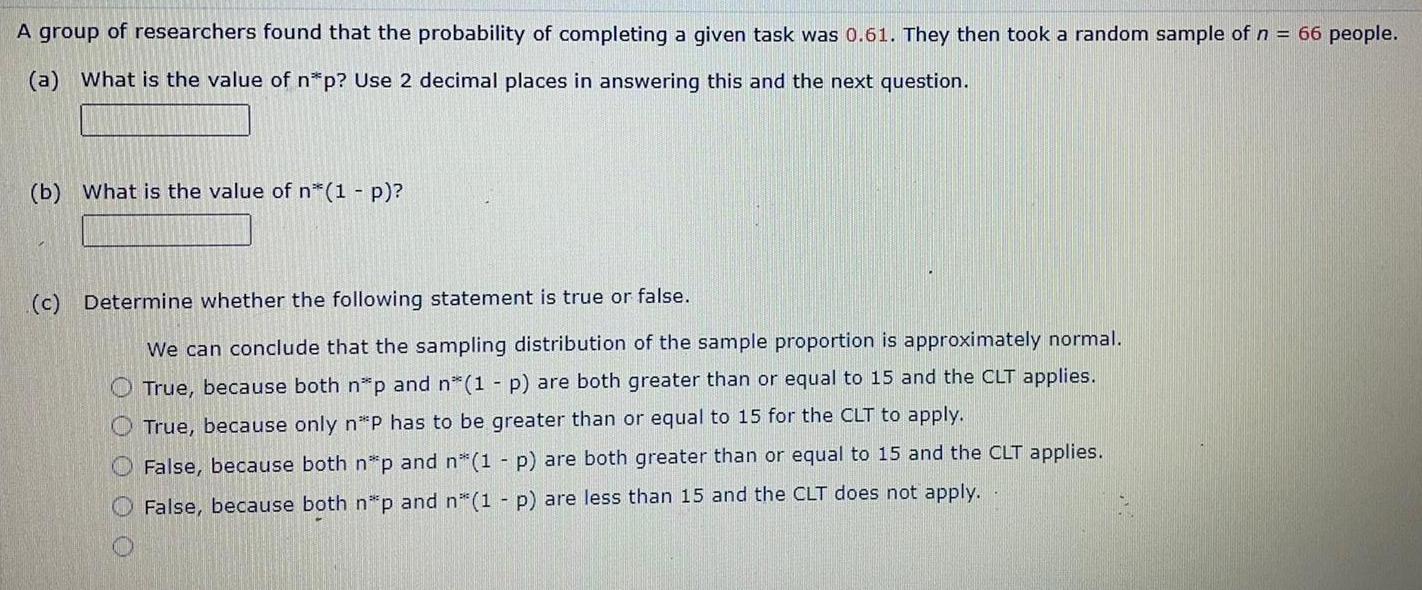
ProbabilityA group of researchers found that the probability of completing a given task was 0.61. They then took a random sample of n = 66 people.
(a) What is the value of n*p? Use 2 decimal places in answering this and the next question.
(b) What is the value of n*(1 - p)?
(c) Determine whether the following statement is true or false.
We can conclude that the sampling distribution of the sample proportion is approximately normal.
True, because both n*p and n*(1 p) are both greater than or equal to 15 and the CLT applies.
True, because only n*P has to be greater than or equal to 15 for the CLT to apply.
False, because both n*p and n*(1 - p) are both greater than or equal to 15 and the CLT applies.
False, because both n*p and n*(1 - p) are less than 15 and the CLT does not apply.

Math
Basic MathA single-serving coffee machine is programmed to dispense 8 ounces of coffee per serving. Occasionally, the machine will start to overfill or underfill cups of coffee and require recalibration. According to the company, the coffee machine requires recalibration if it overfills or underfills cups of coffee by 1.5 or more ounces.
Determine the probability that a randomly selected cup of coffee was underfilled or overfilled by more than 1.5 ounces. Assume the distribution of the amounts of all coffee dispensed by the machine are normally distributed with a mean of 8 ounces and a standard deviation of 1.13 ounces.
The probability that a randomly selected cup of coffee is overfilled or underfilled by 1.5 ounces is
Math
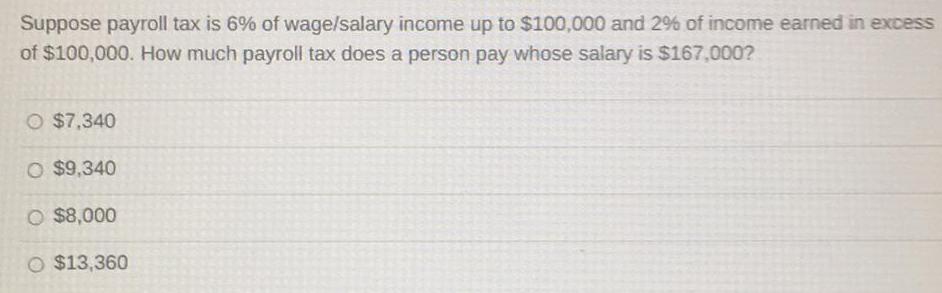
Basic MathSuppose payroll tax is 6% of wage/salary income up to $100,000 and 2% of income earned in excess of $100,000. How much payroll tax does a person pay whose salary is $167,000?
$7,340
$9,340
$8,000
$13,360

Math
Basic MathCarson has a smart phone data plan that costs $35 per month that includes 10 GB of data, but will charge an extra $15 per GB over the included amount. How much would Carson have to pay in a month where he used 3 GB over the limit? How much would Carson have to pay in a month where he used went over by x GB?

Math
Basic MathVaccinations are intended to prevent illness. Suppose a flu vaccine is determined to be effective for 52% of patients administered the shot. A random sample of 75 people will be selected from the population.
(a) What is the population proportion of success in the above scenario?
(b) Calculate the mean of the sampling distribution of the sample proportion of people for whom the shot was effective.
(c) Calculate the standard deviation of the sampling distribution of the sample proportion of people for whom the shot was effective. (Round your answer to three decimal places.)
![Nanette must pass through three doors as she walks from her company's foyer to her office. Each of
these doors may be locked or unlocked.
Let C be the event that at least two doors are in the same condition. List the outcomes of C. [Let "L"
designate "locked" and U" designate "unlocked".]
{LLL, LLU, LUL, LUU, ULL, ULU, UUL, UUU}
(LLL, UUU, LLU, LUL, ULL}
LLU, LUL, ULL, LUU, ULU, UUL}
O none of these](https://media.kunduz.com/media/sug-question/raw/56306630-1658164096.177321.jpeg?w=256)
Math
Basic MathNanette must pass through three doors as she walks from her company's foyer to her office. Each of
these doors may be locked or unlocked.
Let C be the event that at least two doors are in the same condition. List the outcomes of C. [Let "L"
designate "locked" and U" designate "unlocked".]
{LLL, LLU, LUL, LUU, ULL, ULU, UUL, UUU}
(LLL, UUU, LLU, LUL, ULL}
LLU, LUL, ULL, LUU, ULU, UUL}
O none of these

Math
FunctionsThe number of people afflicted with the common cold in teh winter months steadily decreased by 205 each year from 2005 until 2010. In 2005, 12,025 people were afflicted.
Find the following:
A- Find the linear function that models the number of people inflicted with the common
cold, C, as a function of the year, t.
B- Find a reasonable domain and range for the function C.
C- If the function C is graphed, find and interpret the x- and y-intercepts.
D- When will the output reach 0?
E- In what year will the number of people be 9,700?

Math
Basic MathFind the savings plan balance after 15 months with an APR of 2% and monthly payments of $300.

Math
Basic Math1. Dora has an after school job at the Children's Zoo. She notices that at one meal, 3 cats
will eat 2 cans of food.
a How much food does 1 cat eat?
b. Write a formula that Dora can use to determine how many cans of food to use for
any given number of cats? (You can use the table method to develop the formula)
c. If there are 12 cats in the Zoo, how many cans of food should Dora use at each
meal time?
Math
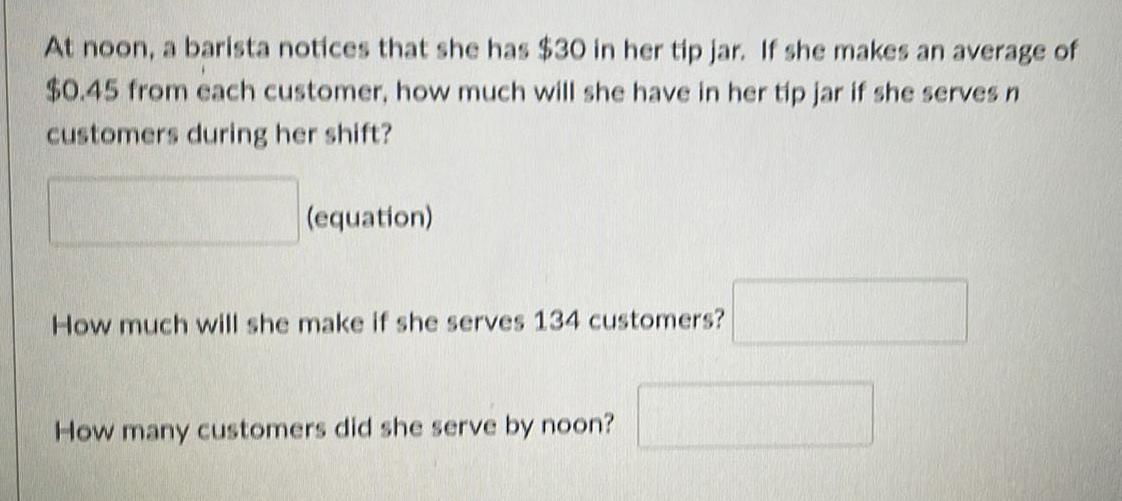
Basic MathAt noon, a barista notices that she has $30 in her tip jar. If she makes an average of $0.45 from each customer, how much will she have in her tip jar if she serves n customers during her shift?
How much will she make if she serves 134 customers?
How many customers did she serve by noon?

Math
Straight linesAnswer the following as true or false. If it is false change the answer to make it true.
a) The intersection of the centroid is the center or gravity for the triangle.
b) The intersection of the centroid is outside the triangle for an obtuse triangle.
c) The intersection of the incenter is sometimes outside the triangle.
d) The intersection of the circumcenter is always outside the triangle.
Math
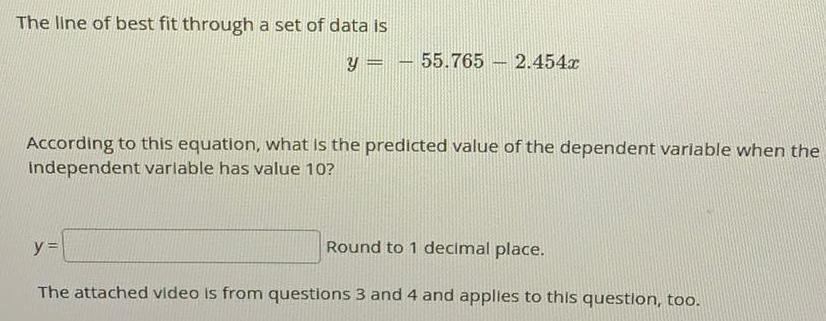
Basic MathThe line of best fit through a set of data is
y = - 55.765 - 2.454x
According to this equation, what is the predicted value of the dependent variable when the
independent variable has value 10?
y =
Round to 1 decimal place.
The attached video is from questions 3 and 4 and applies to this question, too.

Math
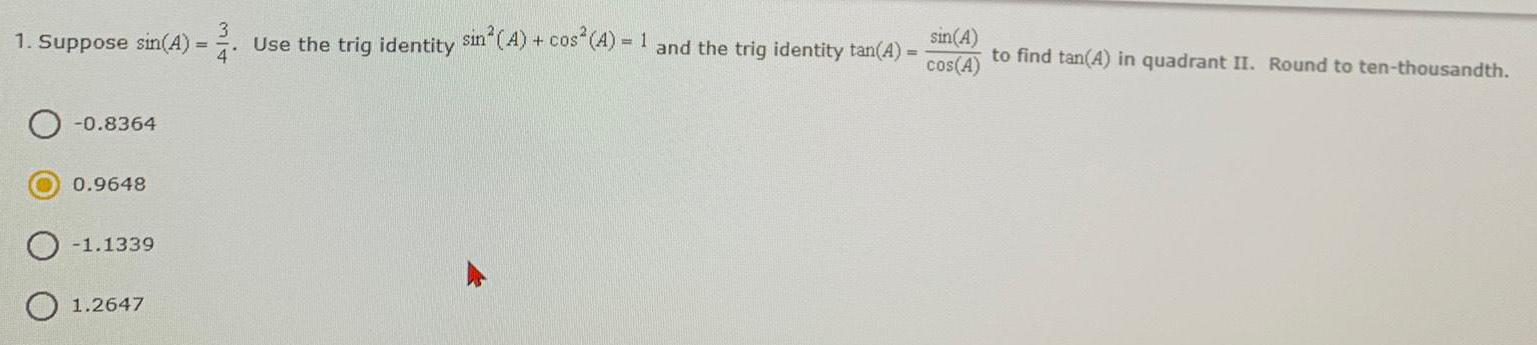
Trigonometry1. Suppose sin(A) = 3/4 Use the trig identity sin² (A) + cos² (A) = 1 and the trig identity tan(A) = sin(A)/cos(A) to find tan(A) in quadrant II. Round to ten-thousandth.
-0.8364
0.9648
-1.1339
1.2647

Math
Basic MathFind an equation of the line described below. Write the equation in slope-intercept form (solved for y), when possible.
Through (-4,7), perpendicular to the y-axis
What is the equation of the line?

Math
Basic MathFind composite numbers that have the following characteristics: a. A number greater than 40 whose prime factorization contains 3 prime numbers that do not repeat
. b. A number greater than 1000 whose prime factorization contains 1 prime number that does not repeat, 1 prime number that repeats 3 times, and 1 prime number that repeats twice.
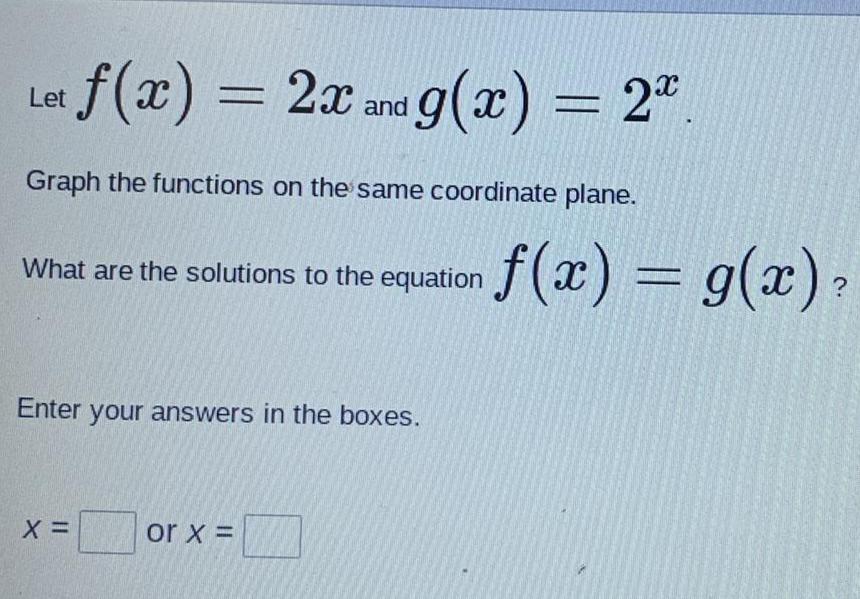
Math
Basic Mathf(x) = 2x and g(x) = 2.^x Graph the functions on the same coordinate plane.
What are the solutions to the equation f(x) = g(x)
Enter your answers in the boxes.

Math
Basic MathThe state of New York reported 1484 live births in which the infants had Down syndrome (trisomy 21) between 2006 and 2010, which averages to about 5.7 cases per week. While the causes of Down syndrome are not fully understood, it is reasonable at this point to assume that live births are independent and the weekly rate is constant. Let X be the count of babies born with Down syndrome in the state of New York in a given week.
(a) What values could X take? Notice how there is no clear limit to this range.
None of the options are correct.
X can take on any positive real number above the mean of X.
X can take on any negative integer value.
X can take on any non-negative whole number.

Math
StatisticsIf the average price of a television in my store is $900 with stock is morally a standard deviation of $50. Assuming my distributed where is:
A. 68% of the computers prices
B. 95% of the computers prices
C. 99.7% of the computers prices
Assuming the data is not normal Chebyshev's states:
D. at least 75% of data is between
E. at least 88.87% of data is between
F. at least 94% of data is between

Math
Basic MathΔBCD What is the length of the other leg? Enter your answer, as a decimal rounded to the nearest tenth, in the box. is a right triangle. The length of the hypotenuse is 19 centimeters. The length of one of the legs is 13 centimeters.

Math
ProbabilityConsider a population of size N = 12, 100 with a mean of u 200 and standard deviation of o = 15.
Compute the following 2-values for sampling distributions of with given sample size.
Suppose a random sample of 56 observations is selected from the population. Calculate the z-value that corresponds to x̄ = 206.
Suppose a random sample of 77 observations is selected from the population. Calculate the z-value that corresponds to x̄ 198.
Suppose a random sample of 60 observations is selected from the population. Calculate the z-value that corresponds to x̄ = 205
Suppose a random sample of 69 observations is selected from the population. Calculate the 2-value that corresponds to x̄ = 200.

Math
StatisticsThe offensive line of a football team is larger than in previous years. The program will list a statistic to show this fact. Which statistic (mean, median, or mode) might be most appropriate in this situation?
Mean
Median
Mode
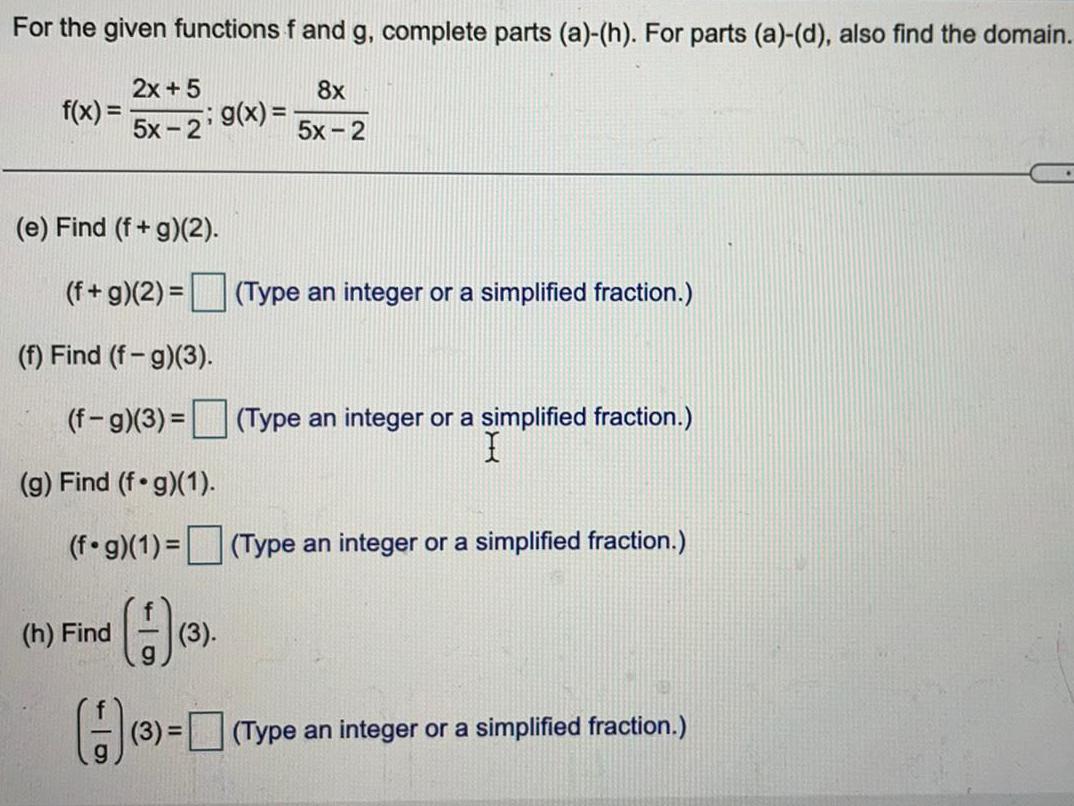
Math
FunctionsFor the given functions f and g, complete parts (a)-(h). For parts (a)-(d), also find the domain.
f (x) = 2x+5 / 5x-2; g(x) = 8x/5x-2

Math
Probability10) A newspaper advertises 5 different movies, 3 plays, and 2 baseball games for the weekend. If a couple selects 3 activities, find the probability that they attend
a. 2 plays and 1 movie.
b. Three movies
c. Two plays and 1 baseball
d. 1 of each type.

Math
ProbabilityThe distribution of all Indian River County grapefruit weights is known to be normally distributed with a mean of 296 grams and a standard deviation of 35 grams. Use this information to determine the following probabilities. Round solutions to four decimal places, if necessary.
Find the probability that a random sample of 52 grapefruit has a mean weight greater than 292 grams.
P(x > 292) =
Find the probability that a random sample of 52 grapefruit has a mean weight between 292 and 295 grams.
P(292< x < 295) =

Math
Basic MathAndy is scuba diving. He starts at sea level and then descends 10 feet in 2 1/2 minutes.
Part A
How would you represent Andy's descent as a unit rate? Express your answer as an integer.
Enter your answer in the box.
feet per minute
Part B
If he continues at this rate, where will Andy be in relation to sea level after 6 minutes?

Math
ProbabilitySometimes it is easier to figure out the probability that something will not happen than the probability that it will. When finding the probability that something will m happen, you are looking at the complement of an event. The complement is the set of all outcomes in the sample space that are not included in the event. Show two ways to solve the problem below, then decide which way you prefer and explain why.
a. The marketing department has interviewed people of all different age groups about the BBQ chicken salad, but now they need information about why the othe salads are less popular. What is the probability that the next person randomly chosen will not prefer the BBQ chicken salad?
b. If the probability of an event A is represented symbolically as P(A), how can you symbolically represent the probability of the complement of event

Math
StatisticsRabies is an often-fatal disease, which is typically transmitted through the bite of an infected animal. The state of Florida has been recording all known cases of rabies for the past 20 years, with data indicating an average rate of 3.6 cases of rabies per week. Let X be the count of rabies cases reported in a given week.
(a) Find the mean of X. (Enter your answer rounded to one decimal place.)
mean of X:
Find the standard deviation of X. (Enter your answer rounded to three decimal places.)
standard deviation of X:
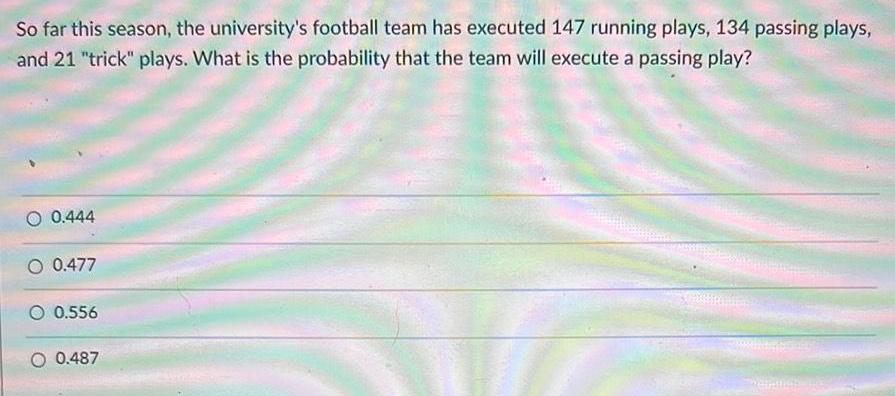
Math
Basic MathSo far this season, the university's football team has executed 147 running plays, 134 passing plays, and 21 "trick" plays. What is the probability that the team will execute a passing play?
0.444
0.477
0.556
0.487
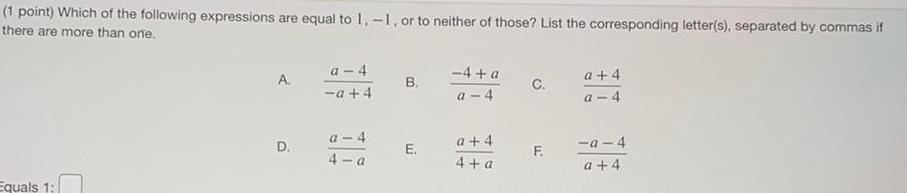
Math
Basic MathWhich of the following expressions are equal to 1,-1, or to neither of those? List the corresponding letter(s), separated by commas if there are more than one.
a. a - 4 / - a + 4
b. -4 + a / a- 4
c. a + 4 / a - 4
d. a - 4 / 4 - a
e. a + 4 / 4 + a
f. -a - 4 / a + 4