Statistics Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
Statistics
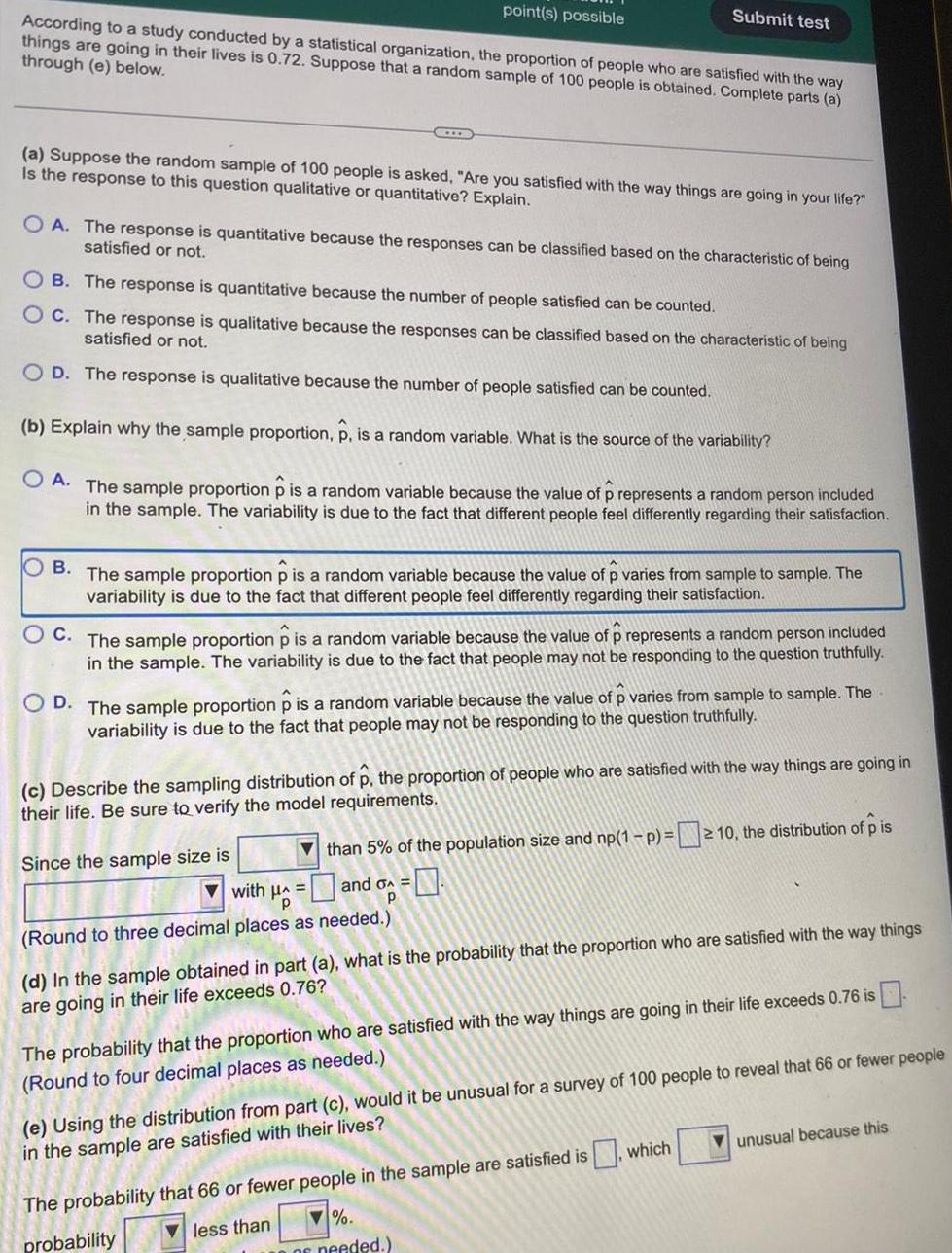
Statisticspoint s possible According to a study conducted by a statistical organization the proportion of people who are satisfied with the way things are going in their lives is 0 72 Suppose that a random sample of 100 people is obtained Complete parts a through e below a Suppose the random sample of 100 people is asked Are you satisfied with the way things are going in your life Is the response to this question qualitative or quantitative Explain Submit test OA The response is quantitative because the responses can be classified based on the characteristic of being satisfied or not OB The response is quantitative because the number of people satisfied can be counted OC The response is qualitative because the responses can be classified based on the characteristic of being satisfied or not OD The response is qualitative because the number of people satisfied can be counted b Explain why the sample proportion p is a random variable What is the source of the variability OA The sample proportion p is a random variable because the value of p represents a random person included in the sample The variability is due to the fact that different people feel differently regarding their satisfaction OB The sample proportion p is a random variable because the value of p varies from sample to sample The variability is due to the fact that different people feel differently regarding their satisfaction C The sample proportion p is a random variable because the value of p represents a random person included in the sample The variability is due to the fact that people may not be responding to the question truthfully OD The sample proportion p is a random variable because the value of p varies from sample to sample The variability is due to the fact that people may not be responding to the question truthfully c Describe the sampling distribution of p the proportion of people who are satisfied with the way things are going in their life Be sure to verify the model requirements 2 than 5 of the population size and np 1 p 10 the distribution of p is with A and G p Round to three decimal places as needed Since the sample size is d In the sample obtained in part a what is the probability that the proportion who are satisfied with the way things are going in their life exceeds 0 76 The probability that the proportion who are satisfied with the way things are going in their life exceeds 0 76 is Round to four decimal places as needed e Using the distribution from part c would it be unusual for a survey of 100 people to reveal that 66 or fewer people in the sample are satisfied with their lives The probability that 66 or fewer people in the sample are satisfied is which less than probability of needed unusual because this
Statistics
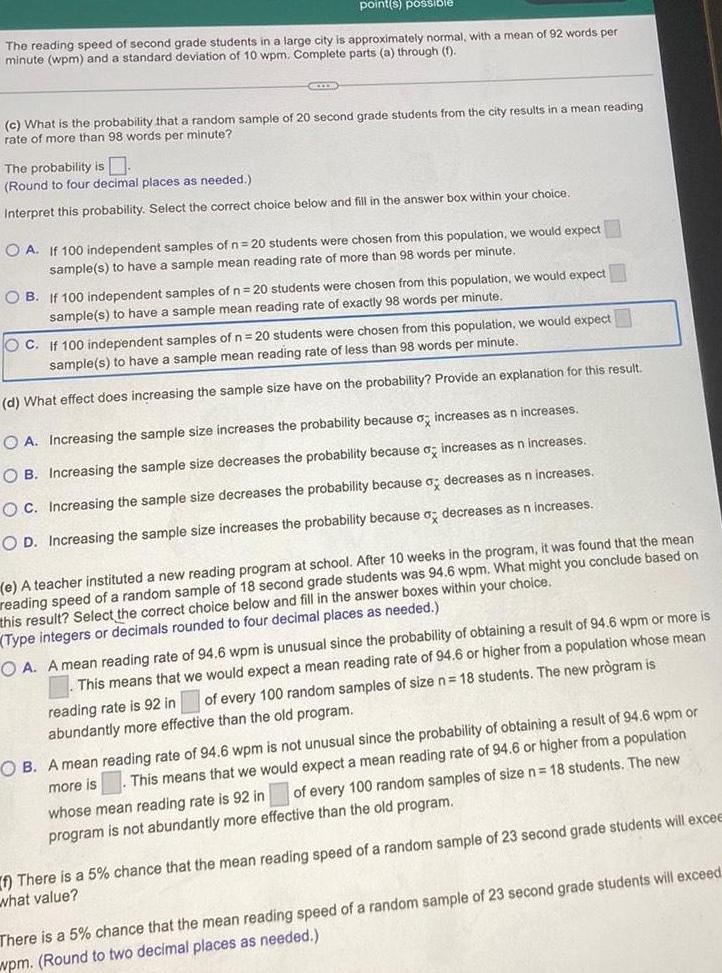
Statisticspoint s possible The reading speed of second grade students in a large city is approximately normal with a mean of 92 words per minute wpm and a standard deviation of 10 wpm Complete parts a through 1 c What is the probability that a random sample of 20 second grade students from the city results in a mean reading rate of more than 98 words per minute The probability is Round to four decimal places as needed Interpret this probability Select the correct choice below and fill in the answer box within your choice OA If 100 independent samples of n 20 students were chosen from this population we would expect sample s to have a sample mean reading rate of more than 98 words per minute OB If 100 independent samples of n 20 students were chosen from this population we would expect sample s to have a sample mean reading rate of exactly 98 words per minute OC If 100 independent samples of n 20 students were chosen from this population we would expect sample s to have a sample mean reading rate of less than 98 words per minute d What effect does increasing the sample size have on the probability Provide an explanation for this result OA Increasing the sample size increases the probability because o increases as n increases OB Increasing the sample size decreases the probability because o increases as n increases OC Increasing the sample size decreases the probability because a decreases as n increases OD Increasing the sample size increases the probability because o decreases as n increases e A teacher instituted a new reading program at school After 10 weeks in the program it was found that the mean reading speed of a random sample of 18 second grade students was 94 6 wpm What might you conclude based on this result Select the correct choice below and fill in the answer boxes within your choice Type integers or decimals rounded to four decimal places as needed OA A mean reading rate of 94 6 wpm is unusual since the probability of obtaining a result of 94 6 wpm or more is This means that we would expect a mean reading rate of 94 6 or higher from a population whose mean of every 100 random samples of size n 18 students The new pr gram is reading rate is 92 in abundantly more effective than the old program OB A mean reading rate of 94 6 wpm is not unusual since the probability of obtaining a result of 94 6 wpm or more is This means that we would expect a mean reading rate of 94 6 or higher from a population of every 100 random samples of size n 18 students The new whose mean reading rate is 92 in program is not abundantly more effective than the old program f There is a 5 chance that the mean reading speed of a random sample of 23 second grade students will excee what value There is a 5 chance that the mean reading speed of a random sample of 23 second grade students will exceed wpm Round to two decimal places as needed

Statistics
Statistics64 The following observations are on time h for a AA 1 5 volt alkaline battery to reach a 0 8 voltage Comparing the Lifetimes of Two Brands of Batteries J of Statistical Educ 2013 online Energizer Ultracell 8 65 8 74 8 91 8 76 8 81 8 52 8 62 8 68 8 76 8 68 8 64 Normal probability plots support the assumption that the population distributions are normal Does the data suggest that the variance of the Energizer population distribution differs from that of the Ultracell population distribution Test the relevant hypotheses using a sig nificance level of 05 Note The two sample test for equality of population means gives a P value of 763 The Energizer batteries are much more expensive than the Ultracell batteries Would you pay the extra money Energizer Ultracell 8 85 8 73 8 70 8 86 8 79

Statistics
ProbabilityIn an effort to budget for future missions NASA is interested in X the amount of fuel required by its space shuttle in a round trip to the moon Specifically they want to prove that the mean amount of fuel required is less than 28 000 kg They wish to perform this hypothesis test using 0 05 Unfortunately due to the expense associated with collecting observations NASA has only the following five samples to analyze all observations are in units of kg 28 150 Suppose the data has an approximately normal distribution Part a 5 points State the appropriate null and alternative hypothesis for this test 27 222 27 928 27 121 27 009 Part b 5 points Identify the test statistic and p value and state the conclusion of the test

Statistics
StatisticsMatch the coefficient of determination to the scatter diagram The scales on the x axis and y axis are the same for each scatter diagram a R 1 b R2 0 62 c R 0 90 a Scatter diagram b Scatter diagram c Scatter diagram Response Response Response Explanatory Explanatory
Statistics
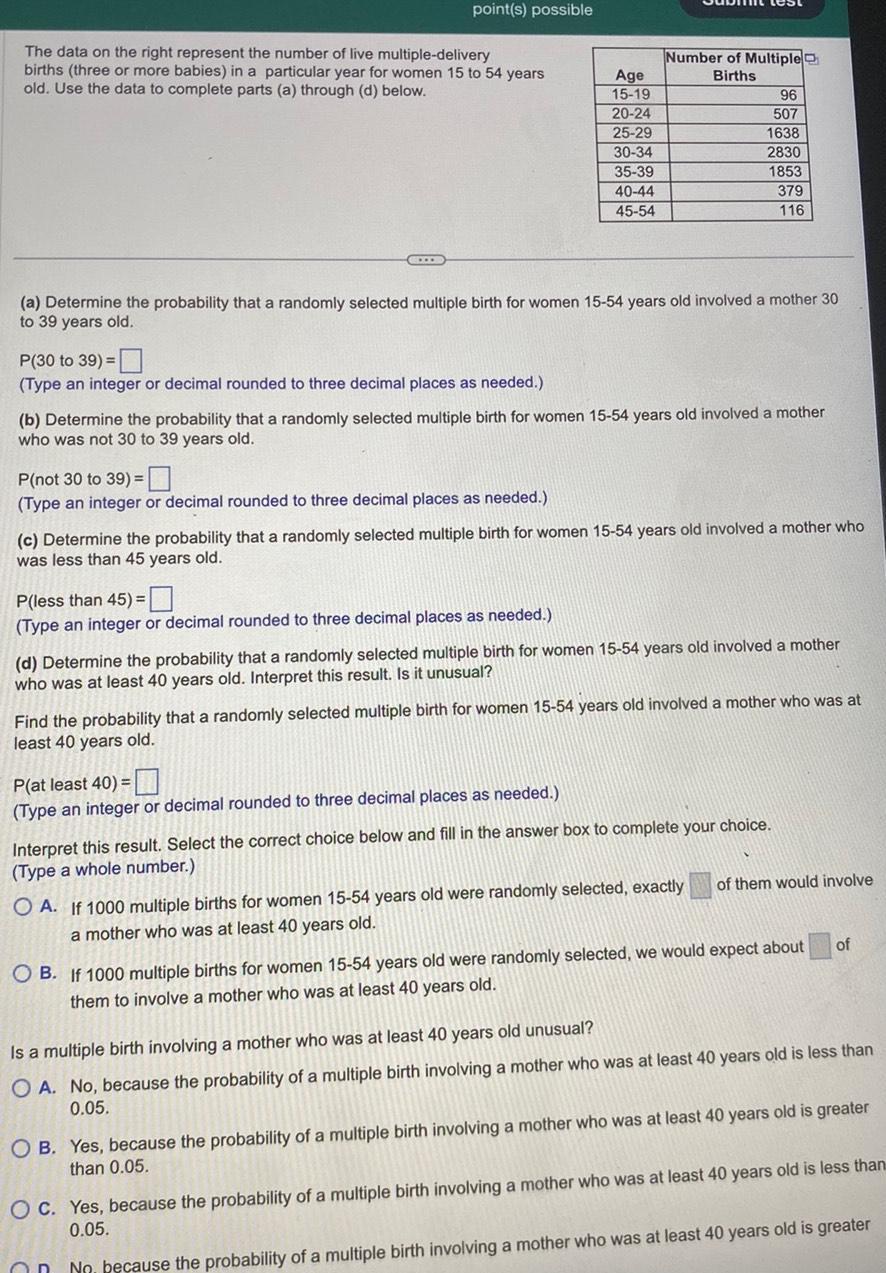
Statisticspoint s possible The data on the right represent the number of live multiple delivery births three or more babies in a particular year for women 15 to 54 years old Use the data to complete parts a through d below P 30 to 39 Type an integer or decimal rounded to three decimal places as needed P not 30 to 39 Type an integer or decimal rounded to three decimal places as needed a Determine the probability that a randomly selected multiple birth for women 15 54 years old involved a mother 30 to 39 years old Age 15 19 20 24 P less than 45 Type an integer or decimal rounded to three decimal places as needed 25 29 30 34 35 39 40 44 45 54 b Determine the probability that a randomly selected multiple birth for women 15 54 years old involved a mother who was not 30 to 39 years old Number of Multiple Births c Determine the probability that a randomly selected multiple birth for women 15 54 years old involved a mother who was less than 45 years old P at least 40 Type an integer or decimal rounded to three decimal places as needed 96 507 1638 2830 1853 379 116 d Determine the probability that a randomly selected multiple birth for women 15 54 years old involved a mother who was at least 40 years old Interpret this result Is it unusual Find the probability that a randomly selected multiple birth for women 15 54 years old involved a mother who was at least 40 years old Interpret this result Select the correct choice below and fill in the answer box to complete your choice Type a whole number OA If 1000 multiple births for women 15 54 years old were randomly selected exactly a mother who was at least 40 years old On of them would involve OB If 1000 multiple births for women 15 54 years old were randomly selected we would expect about them to involve a mother who was at least 40 years old of Is a multiple birth involving a mother who was at least 40 years old unusual OA No because the probability of a multiple birth involving a mother who was at least 40 years old is less than 0 05 OB Yes because the probability of a multiple birth involving a mother who was at least 40 years old is greater than 0 05 OC Yes because the probability of a multiple birth involving a mother who was at least 40 years old is less than 0 05 No because the probability of a multiple birth involving a mother who was at least 40 years old is greater
Statistics
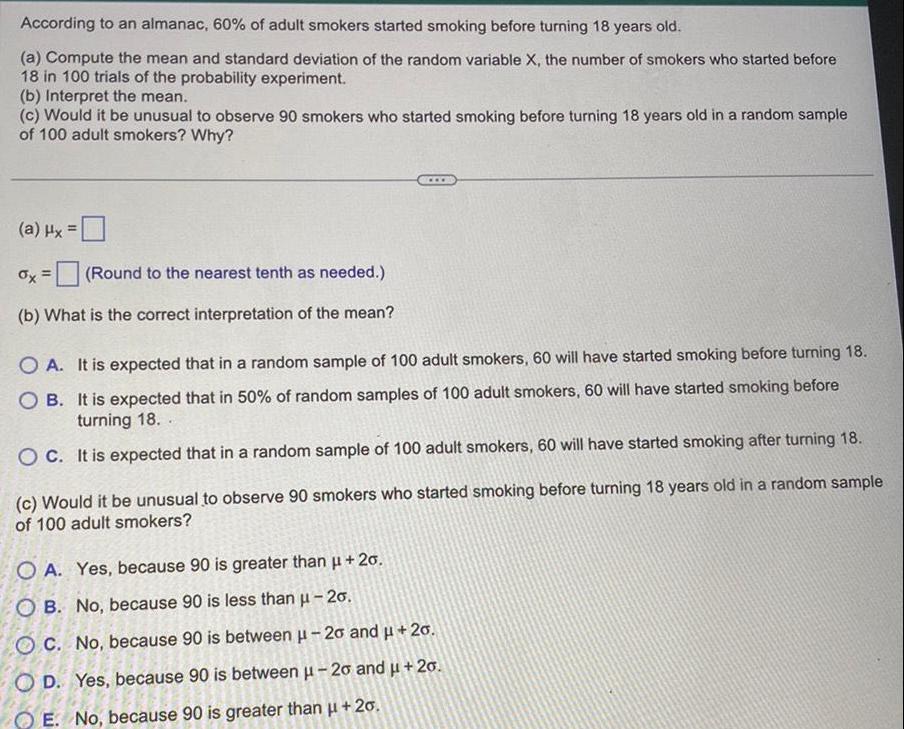
StatisticsAccording to an almanac 60 of adult smokers started smoking before turning 18 years old a Compute the mean and standard deviation of the random variable X the number of smokers who started before 18 in 100 trials of the probability experiment b Interpret the mean c Would it be unusual to observe 90 smokers who started smoking before turning 18 years old in a random sample of 100 adult smokers Why a Hx x Round to the nearest tenth as needed b What is the correct interpretation of the mean OA It is expected that in a random sample of 100 adult smokers 60 will have started smoking before turning 18 OB It is expected that in 50 of random samples of 100 adult smokers 60 will have started smoking before turning 18 OC It is expected that in a random sample of 100 adult smokers 60 will have started smoking after turning 18 c Would it be unusual to observe 90 smokers who started smoking before turning 18 years old in a random sample of 100 adult smokers OA Yes because 90 is greater than 20 OB No because 90 is less than 20 OC No because 90 is between 20 and 20 OD Yes because 90 is between 20 and 20 OE No because 90 is greater than 20

Statistics
StatisticsW Use the accompanying radiation levels in kg different cell phones Find the percentile P40 W for 50 0 26 0 28 0 28 0 51 0 57 0 61 0 62 0 68 0 74 0 81 0 89 0 90 0 93 0 93 0 93 0 97 1 00 1 00 1 07 1 09 1 09 1 12 1 13 1 14 1 15 1 16 1 17 1 19 1 21 1 21 1 22 1 24 1 25 1 26 1 28 1 28 1 30 1 30 1 32 1 33 1 36 1 40 1 41 1 41 1 45 1 51 1 52 1 53 1 54 1 57

Statistics
StatisticsThe body temperatures of a group of healthy adults have a bell shaped distribution with a mean of 98 11 F and a standard deviation of 0 51 F Using the empirical rule find each approximate percentage below a What is the approximate percentage of healthy adults with body temperatures within 2 standard deviations of the mean or between 97 09 F and 99 13 F b What is the approximate percentage of healthy adults with body temperatures between 96 58 F and 99 64 F a Approximately of healthy adults in this group have body temperatures within 2standard deviations of the mean or between 97 09 and 99 13 F Type an integer or a decimal Do not round b Approximately of healthy adults in this group have body temperatures between 96 58 F and 99 64 F Type an integer or a decimal Do not round

Statistics
StatisticsA group of adult males has foot lengths with a mean of 26 81 cm and a standard deviation of 1 37 cm Use the range rule of thumb for identifying significant values to identify the limits separating values that are significantly low or significantly high Is the adult male foot length of 23 6 cm significantly low or significantly high Explain Significantly low values are Type an integer or a decimal cm or lower Do not round Significantly high values are cm or higher Type an integer or a decimal Do not round Select the correct choice below and fill in the answer box es to complete your choice O A The adult male foot length of 23 6 cm is significantly low because it is less than Type an integer or a decimal Do not round OB The adult male foot length of 23 6 cm is not significant because it is between Type integers or decimals Do not round cm cm and O C The adult male foot length of 23 6 cm is significantly high because it is greater than cm Type an integer or a decimal Do not round cm
Statistics
ProbabilityDetermine whether the following results appear to have statistical significance and also determine whether the results have practical significance Most people have IQ scores between 70 and 130 For approximately 39 99 you can purchase a PC or Mac program from HighlQPro that is claimed tox increase your IQ score by 10 to 20 points The program claims to be the only proven IQ increasing software in the brain training market but researchers could find no substantial data supporting that claim so suppose that in a study of 13 subjects using the program the average increase in 10 score is 14 IQ points There is a 2 chance of getting such results if the program has no effect Does the IQ increasing software have statistical significance A No the software is not statistically significant because the results are likely to occur by chance B Yes the software is statistically significant because the results are likely to occur by chance C No the software is not statistically significant because the results are unlikely to occur by chance O D Yes the software is statistically significant because the results are unlikely to occur by chance Does the IQ increasing software have practical significance A No the software is not practically significant because the number of IQ points gained is very small OB Yes the software is practically significant because the results are too unlikely to occur by chance C Yes the software is practically significant because the number of IQ points gained is large enough to be considered practically significant
Statistics
StatisticsListed below are the annual tuition amounts of the 10 most expensive colleges in a country for a recent year What does this Top 10 list tell us about the population of all of that country s college tuiti 51 281 52 360 51 448 52 901 54 025 50 877 53 420 52 360 50 783 53 646 Find the mean midrange median and mode of the data set The mean of the data set is Round to two decimal places as needed The midrange of the data set is Round to two decimal places as needed The median of the data set is Round to two decimal places as needed What is are the mode s of the data set Select the correct choice below and if necessary fill in the answer box within your choice OA The mode s of the data set is are Use a comma to separate answers as needed Round to two decimal places as needed OB There is no mode What does this Top 10 list tell us about the population of all the country s college tuitions O A All colleges have tuitions around the mean OB All colleges have tuitions around the median OC All colleges have tuitions around the mode C AU CO

Statistics
ProbabilityEight student essays are submitted for a writing contest A group of English professors will choose 4 of these essays to feature in the college newspaper In how many ways can this be done 4 1680 24 hm

Statistics
Statistics6 The expected value was computed for the number of customers at a Mango Whip stand and it was found that the expected number of customers for a day in July is 117 We then know that on July 8 there should be 117 customers at that Mango Whip stand ADAY GENTOT K 7 A carnival game has an expected payout of 6 Which of the following is a correct interpretation True or You will win 6 each time you play the game b If you played the game 100 times you could expect to win 6 C If you played the game 100 times you could expect to win 600 d There is no way to lose money playing this game 8 An airline has determined that the expected number of no shows for their regular Flight 007 is 23 Which of the following is NOT a reasonable interpretation of this fact a C a C e a If the airline averaged the number of no shows per trip for Flight 007 for a year the average would be about 23 b The number of no shows for Flight 007 could be zero on one of the trips they make Each time Flight 007 goes there are 23 passengers with tickets who did not make the flight d For 100 trips the total number of no shows for Flight 007 would be about 2300 False 9 Your favorite charity is holding a game night benefit One of the games is Fun Toss where players win 1 if they land on red 3 if they land on blue and 5 if they land on green The expected winnings for those playing Fun Toss is 1 50 per game Circle all the true statements regarding the game If Sophie plays a game of Fun Toss she will most likely win 1 50 b If Brandon plays Fun Toss 100 times he should expect his winnings to total about 150 Phil is likely to win an average of 3 if he plays this game many times d If Will plays Fun Toss 200 times it is likely he will win an average of 1 50 per game The more times Sarah plays Fun Toss the more likely she is to win 1 50 on her next toss
Statistics
StatisticsFind the a mean b median c mode and d midrange for the data and then e answer the given questions Listed below are the highest amounts of net worth in millions of dollars of all celebrities What do the results tell us about the population of all celebrities Based on the nature of the amounts what can be inferred about their precision 285 195 190 180 a Find the mean 170 170 150 150 150 150 D The mean is million Type an integer or a decimal rounded to one decimal place as needed b Find the median The median is million Type an integer or a decimal rounded to one decimal place as needed c Find the mode Select the correct choice below and if necessary fill in the answer box to complete your choice OA The mode s is are million Type an integer or a decimal Do not round Use a comma to separate answers as needed B The is no mod d Find the midrange The midrange is million Type an integer or a decimal rounded to one decimal place as needed e What do the results tell us about the population of all celebrities O A The results tell us that the most common celebrity net worth is the mode but all other celebrities are expected to have net worths approximately equal to the mean median or midrange B The results tell us that all celebrities are expected to have amounts of net worth approximately equal to one of the measures of center found in parts a through d C Apart from the fact that all other celebrities have amounts of net worth lower than those given nothing meaningful can be known about the population
Statistics
StatisticsFind the range variance and standard deviation for the given sample data if possible If the measures of variation can be obtained for these values do the results make sense Biologists conducted experiments to determine whether a deficiency of carbon dioxide in the soil affects the phenotypes of peas Listed below are the phenotype codes where 1 smooth yellow 2 smooth green 3 wrinkled yellow and 4 wrinkled green 21 2 24 2 4 1 22 2 3 2 2 2 2 2 2 2 20 Can the range of the sample data be obtained for these values Choose the correct answer below and if necessary fill in the answer box within your choice OA The range of the sample data is Type an integer or a decimal Do not round B The range of the sample data cannot be calculated Can the standard deviation of the sample data be obtained for these values Choose the correct answer below and if necessary fill in the answer box within your choice OA The standard deviation of the sample data is Round to one decimal place as needed B The standard deviation of the sample data cannot be calculated Can the variance of the sample data be obtained for these values Choose the correct answer below and if necessary fill in the answer box within your choice A The variance of the sample data is Round to one decimal place as needed B The variance of the sample data cannot be calculated Do the results make sense O A While the measures of variation can be found they do not make sense because the data are nominal they don t measure or count anything B It makes sense that the measures of variation cannot be calculated because there is not a large enough sample size to calculate the measures of variation C The measures of variation make sense because the data is numeric so the spread between the values is meaningful D The measures of variation do not make sense because the standard deviation cannot be greater than the variance
Statistics
StatisticsA sample of blood pressure measurements is taken for a group of adults and those values mm Hg are listed below The values are matched so that 10 subjects each have a systolic and diastolic measurement Find the coefficient of variation for each of the two samples then compare the variation Systolic 119 130 156 97 154 123 116 134 125 120 Diastolic 82 77 75 51 90 89 57 63 72 83 The coefficient of variation for the systolic measurements is Type an integer or decimal rounded to one decimal place as needed The coefficient of variation for the diastolic measurements is Type an integer or decimal rounded to one decimal place as needed Compare the variation The coefficients of variation for each data set are measurements vary measurements Therefore the systolic the diastolic
Statistics
Statistics3 The brain volumes cm of 20 brains have a mean of 1124 6 cm and a standard deviation of 124 7 cm Use the given standard deviation and the range rule of thumb to identify the limits separating values that are significantly low or significantly high For such data would a brain volume of 1364 0 cm be significantly high Significantly low values are Type an integer or a decimal 3 cm or lower Do not round 3 cm or higher Do not round Significantly high values are Type an integer or a decimal Is 1364 0 cm significantly high O A No because it is between the limits separating values OB No because it is below the lower limit separating value OC Yes because it is below the lower limit separating value O D Yes because it is above the upper limit separating value OE No because it is above the upper limit separating value OF Yes because it is between the limits separating values
Statistics
StatisticsA group of adult males has foot lengths with a mean of 28 48 cm and a standard deviation of 1 36 cm Use the range rule of thumb for identifying significant values to identify the limits separating values that are significantly low or significantly high Is the adult male foot length of 31 5 cm significantly low or significantly high Explain Significantly low values are cm or lower Type an integer or a decimal Do not round Significantly high values are cm or higher Type an integer or a decimal Do not round Select the correct choice below and fill in the answer box es to complete your choice The adult male foot length of 31 5 cm is significantly OA low because it is less than cm Type an integer or a decimal Do not round The adult male foot length of 31 5 cm is not significant cm and B because it is between cm Type integers or decimals Do not round The adult male foot length of 31 5 cm is significantly cm Type an integer or a decimal Do not round O c high because it is greater than IS sh 9 4
Statistics
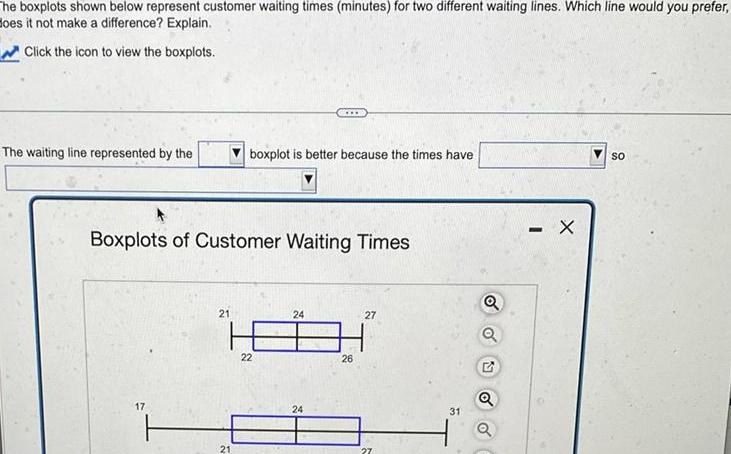
StatisticsThe boxplots shown below represent customer waiting times minutes for two different waiting lines Which line would you prefer does it not make a difference Explain Click the icon to view the boxplots The waiting line represented by the 17 Boxplots of Customer Waiting Times F 21 boxplot is better because the times have 21 24 18 22 www 24 26 27 27 31 Q Q Q Q X SO
Statistics
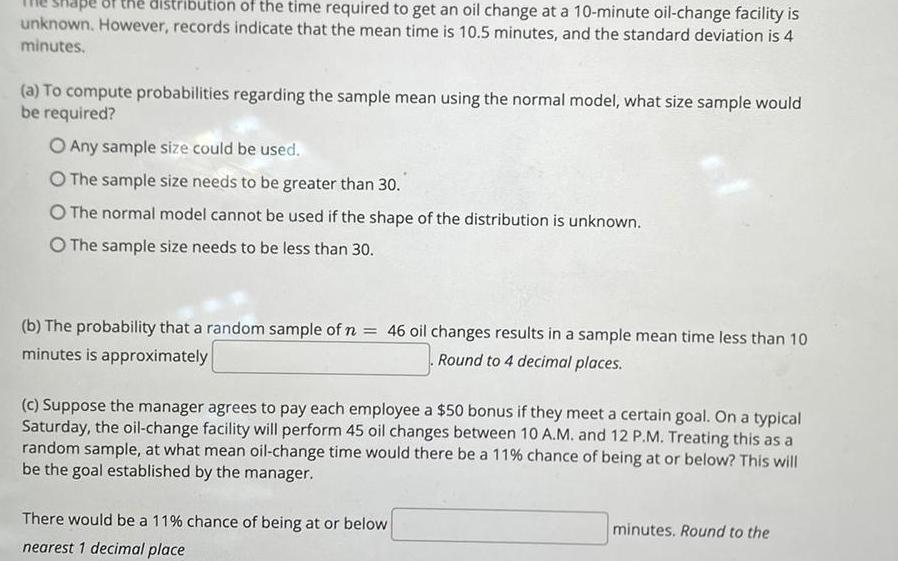
Statisticsdistribution of the time required to get an oil change at a 10 minute oil change facility is unknown However records indicate that the mean time is 10 5 minutes and the standard deviation is 4 minutes a To compute probabilities regarding the sample mean using the normal model what size sample would be required O Any sample size could be used O The sample size needs to be greater than 30 O The normal model cannot be used if the shape of the distribution is unknown O The sample size needs to be less than 30 b The probability that a random sample of n 46 oil changes results in a sample mean time less than 10 minutes is approximately Round to 4 decimal places c Suppose the manager agrees to pay each employee a 50 bonus if they meet a certain goal On a typical Saturday the oil change facility will perform 45 oil changes between 10 A M and 12 P M Treating this as a random sample at what mean oil change time would there be a 11 chance of being at or below This will be the goal established by the manager There would be a 11 chance of being at or below nearest 1 decimal place minutes Round to the
Statistics
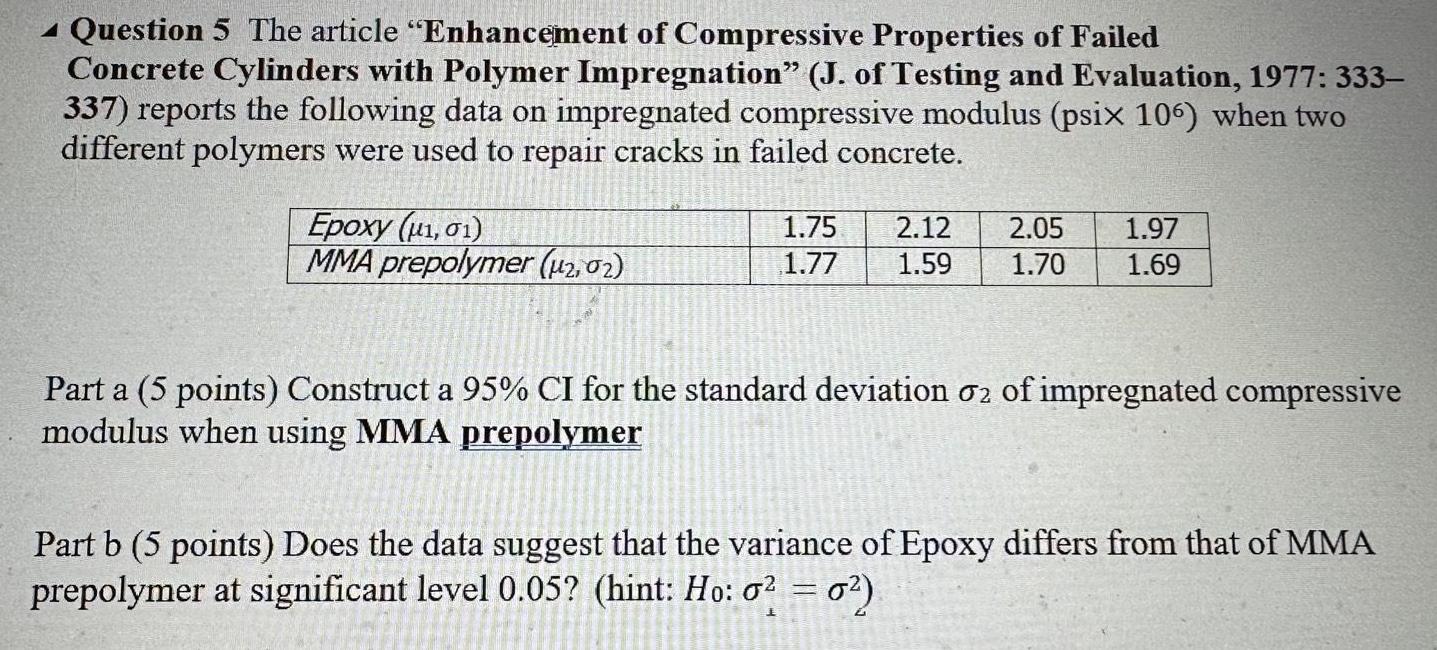
StatisticsQuestion 5 The article Enhancement of Compressive Properties of Failed Concrete Cylinders with Polymer Impregnation J of Testing and Evaluation 1977 333 337 reports the following data on impregnated compressive modulus psix 106 when two different polymers were used to repair cracks in failed concrete Epoxy 1 01 MMA prepolymer 2 02 1 75 2 12 2 05 1 77 1 59 1 70 1 97 1 69 Part a 5 points Construct a 95 CI for the standard deviation 02 of impregnated compressive modulus when using MMA prepolymer Part b 5 points Does the data suggest that the variance of Epoxy differs from that of MMA prepolymer at significant level 0 05 hint Ho 0 0
Statistics
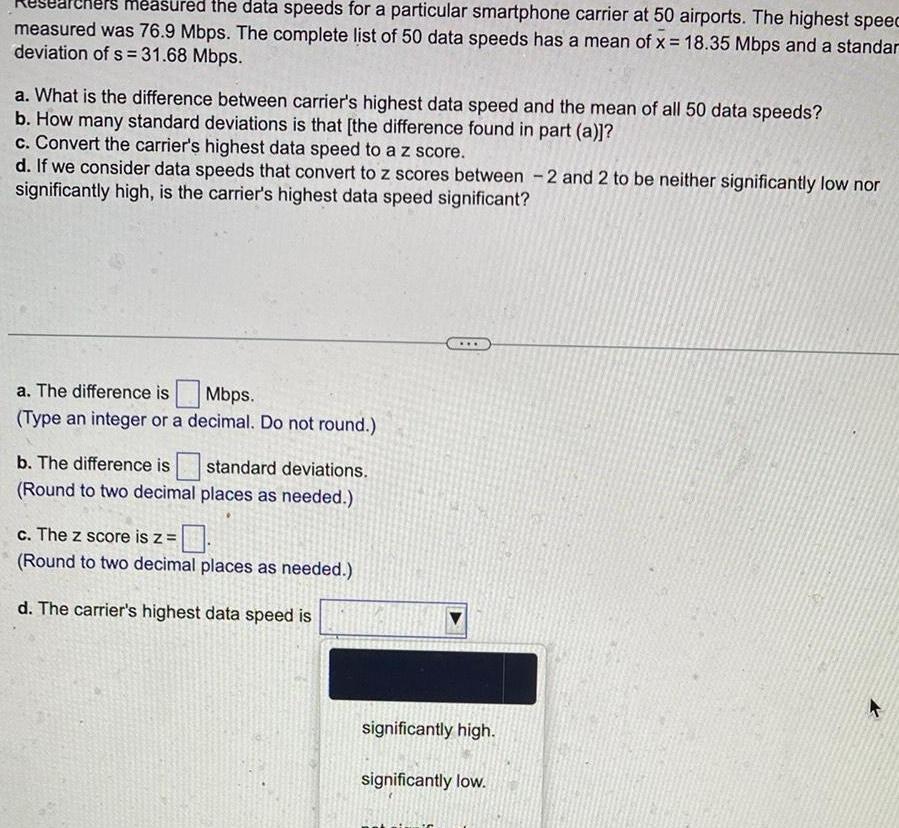
Statisticsmeasured the data speeds for a particular smartphone carrier at 50 airports The highest speec measured was 76 9 Mbps The complete list of 50 data speeds has a mean of x 18 35 Mbps and a standar deviation of s 31 68 Mbps a What is the difference between carrier s highest data speed and the mean of all 50 data speeds b How many standard deviations is that the difference found in part a c Convert the carrier s highest data speed to a z score d If we consider data speeds that convert to z scores between 2 and 2 to be neither significantly low nor significantly high is the carrier s highest data speed significant a The difference is Mbps Type an integer or a decimal Do not round b The difference is standard deviations Round to two decimal places as needed c The z score is z Round to two decimal places as needed d The carrier s highest data speed is significantly high significantly low
Statistics
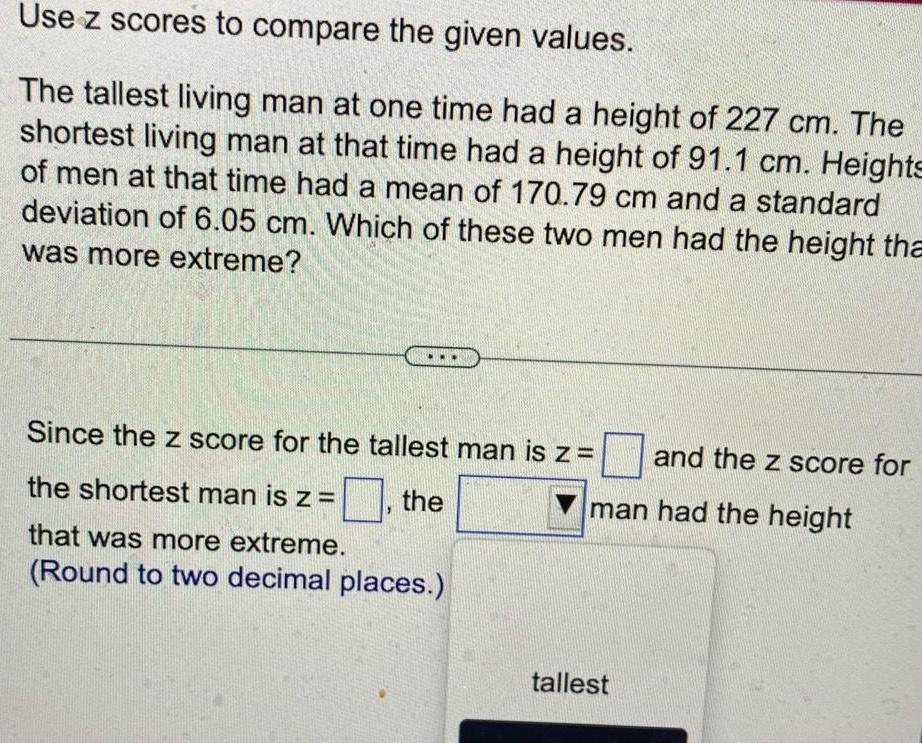
StatisticsUse z scores to compare the given values The tallest living man at one time had a height of 227 cm The shortest living man at that time had a height of 91 1 cm Heights of men at that time had a mean of 170 79 cm and a standard deviation of 6 05 cm Which of these two men had the height tha was more extreme Since the z score for the tallest man is z the shortest man is z the that was more extreme Round to two decimal places and the z score for man had the height tallest

Statistics
StatisticsLet X denote the life length in hours of a battery Suppose X is known to be normally distributed with standard deviation o 2 25 hours A random sample of 12 batteries has an average life of x 51 3 hours We are interested in determining whether there is evidence to support the claim that mean battery life exceeds 50 hours Using a level of significance of 0 05 answer the following questions Part a 4 points State the null and alternative hypothesis for the appropriate hypothesis test Part b 5 points Identify the test statistic and p value Part c 3 points State the conclusion of the test in the problem context Part d 5 points What is the Type II error probability for the test if the true mean life is 51 0 hours Part e 3 points If the true mean life is 51 0 hours what is the power of the test Part f 5 points What value of n is required to satisfy a 0 05 and 0 01

Statistics
StatisticsA certain component is critical to the operation of an electrical system and must be replaced immediately upon failure If the mean life of this type of component is 85 hours and its standard deviation is 34 hours find the minimum number of these components to stock so that the probability that the system is in continual operation for the next 2000 hours is at least 0 95
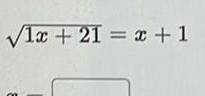
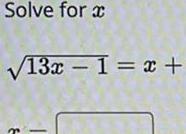
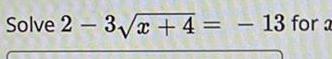
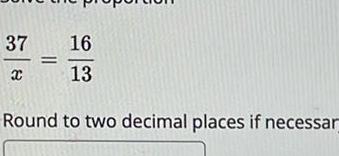
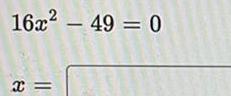

Statistics
ProbabilityA study is being conducted to determine whether a particular exercise program is effective at reducing the mean blood cholesterol level on males between the ages of 35 and 50 Six subjects participated in the program and their cholesterol levels before and after the program are as follows Blood Cholesterol Level Before 265 240 Subject 1 23456 2 4 258 295 251 225 Using this data we wish to test the following hypothesis using a level of significance of 0 1 where 1 denotes the mean blood cholesterol level before the program and uz denotes the mean blood cholesterol level after the program Ho 120 H 12 0 After 229 231 227 240 238 226 Answer questions a through d assuming that you have chosen to use a paired t test Part a 5 points State any assumptions that are required to perform this test and modify the hypothesis by D 1 2 Part b 5 points Identify the test statistic and p value Part c 5 points State the conclusion resulting from the test Part d 5 points Construct a confidence bound that is relevant to this problem Show that this confidence bound verifies your conclusion from part c
Statistics
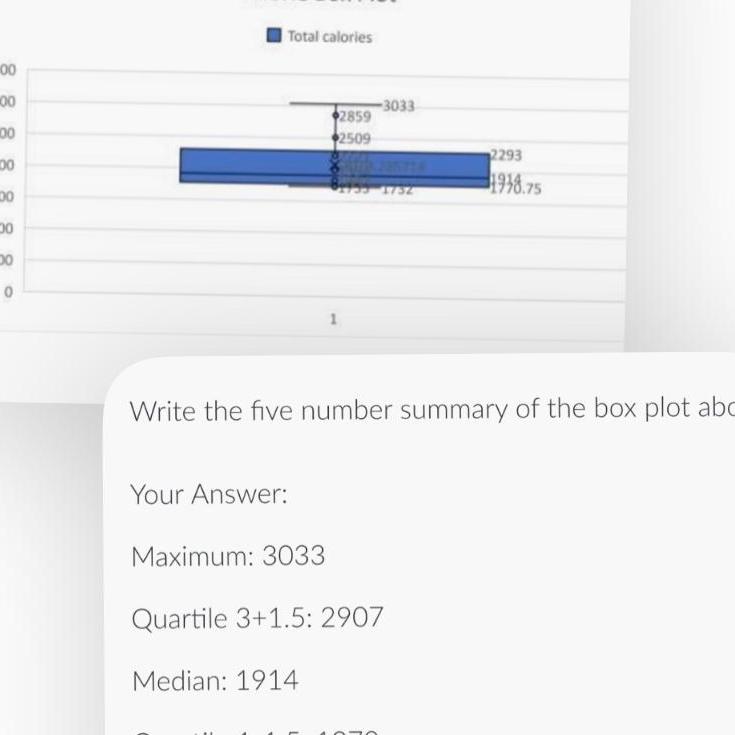
Statistics00 888 00 00 00 30 0 Total calories Your Answer 2859 2509 Median 1914 3033 81733 1732 1 Write the five number summary of the box plot abc Maximum 3033 Quartile 3 1 5 2907 2293 1938 75

Statistics
ProbabilityWhy is Depreciation and amoritization expenses treated different from other expenses

Statistics
Statisticsthe cost of capital Is there a cost of retained earnings Explain briefly conceptually Chapter 10 Name two advant

Statistics
ProbabilityHow do you interpret the NPV Profitability Index e g PI 1 20 or NPV 2 million on an investment of 10 million what does it mean Chapter 11


Statistics
Statistics6 In a Gallup poll of 1000 adults were asked if they consume alcohol beverages and 55 of them said that they did Construct a 99 confidence interval of the proportion of all adults who consume alcohol beverages

Statistics
ProbabilityA brand name has a 18 recognition rate Assume the owner of the brand wants to verify that rate by beginning with a small sample of 25 randomly selected consumers Complete parts a through c below a What is the probability that exactly 6 of the selected consumers recognize the brand name P 0118 n 25 b What is the probability that all of the selected consumers recognize the brand name c What is the probability that at least 5 of the selected consumers recognize the brand name
Statistics
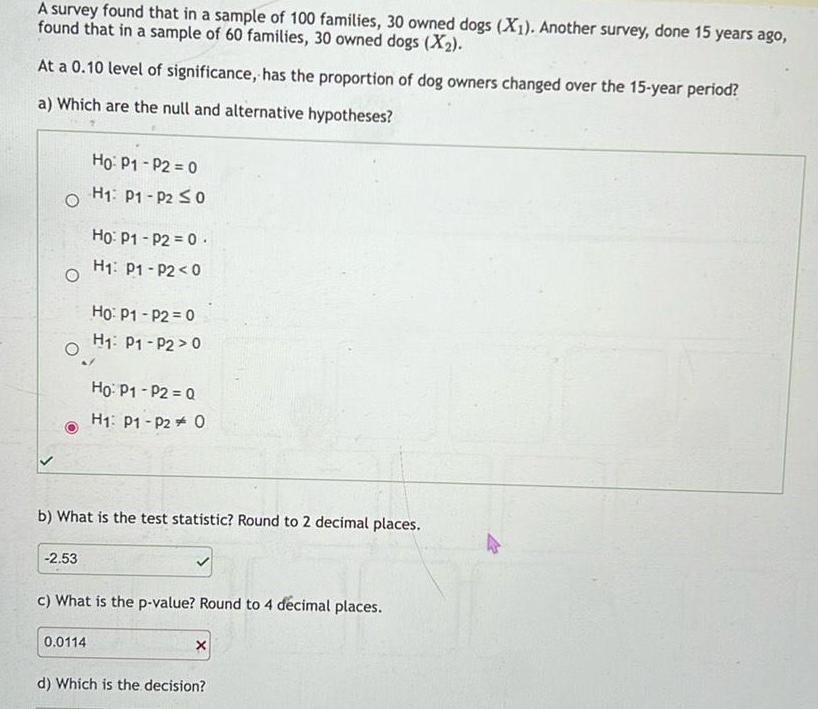
StatisticsA survey found that in a sample of 100 families 30 owned dogs X1 Another survey done 15 years ago found that in a sample of 60 families 30 owned dogs X At a 0 10 level of significance has the proportion of dog owners changed over the 15 year period a Which are the null and alternative hypotheses O O 2 53 Ho P1 P2 0 H P1 P2 0 Ho P1 P2 0 H P1 P2 0 0 0114 Ho P1 P2 0 H P1 P2 0 b What is the test statistic Round to 2 decimal places Ho P1 P2 Q H1 P1 P2 O c What is the p value Round to 4 d cimal places X d Which is the decision

Statistics
StatisticsA sample of 40 earthquake depths has a mean of 8 km Use a 0 01 significance level to test the claim of a seismologist that these earthquakes are from a population that has a mean depth less than 10 km Assume that the population standard deviation is known to be 4 km Ho Ha Test Statistics P value Decision

Statistics
Statistics5 The overhead reach distances of adult females are normally distributed with a mean of 220 cm and a standard deviation of 4 cm a Find the probability that an individual distance is greater than 230 cm b Find the probability that the mean for 25 randomly selected distances is greater than 230 cm

Statistics
Probability1 PART 5 FOOD COMPOUND PROBABILITY At one of your restaurants a variety of desserts are placed on the counter for people to buy at the end of their meals Some of your best sellers include cheesecake cookies and apple pie Label the plates below with the three desserts The first few have been done for you cookies Cheese cake COLORO cheesecake G apple pic Apple Pie Apple Pie lates Apple Pie greke Probability in deamal Cookies cheese cake OSAICODS USE THE ABOVE INFORMATION TO ANSWER THE QUESTIONS BELOW Cookies 3 cheese cake What is the probability of a person randomly selecting a cheesecake putting it back and then selecting a cookie Express your answer as a fraction decimal and percent In decimal 0 3 in percent 30 9 10 023 30 0 Probability G 2 in fraction 3 in What is the probability of a person randomly selecting an apple pie eating it and then selecting another apple pie Express your answer as a fraction decimal and percent 9 0 33 33 33 Probability In decimal 0 33 in percent 33 33 What is the probability of a person randomly selecting a cookie giving it to their friend and then randomly selecting a cheesecake Express your answer as a fraction decimal and percent Probability in fraction 0 33 Probability in fraction O O in percent 33 33 0 33 33 33 4 What is the probability of a person randomly selecting an apple pie putting it back and then selecting a cookie Express your answer as a fraction decimal and percent 3 30 fraction 3 decimal 0 3 percent 30 What is the probability of a person randomly selecting a cheesecake eating it and ther 3 0 3 TO selecting an apple pie Express your answer as a fraction decimal and percent

Statistics
StatisticsConsider the following table representing a probability distribution What is the expected value for this distribution Round to the nearest hundredth X 1 2 3 1 5 0 5 19 1 75 P X 1 2 1 4 1 4

Statistics
ProbabilityPART 5 FOOD COMPOUND PROBABILITY At one of your restaurants a variety of desserts are placed on the counter for people to buy at the end of their meals Some of your best sellers include cheesecake cookies and apple pie Label the plates below with the three desserts The first few have been done for you 00 cookies cheesecake apple pic OOOO0 USE THE ABOVE INFORMATION TO ANSWER THE QUESTIONS BELOW What is the probability of a person randomly selecting a cheesecake putting it back and then selecting a cookie Express your answer as a fraction decimal and percent 2 What is the probability of a person randomly selecting an apple pie eating it and then selecting another apple pie Express your answer as a fraction decimal and percent 3 What is the probability of a person randomly selecting a cookie giving it to their friend and then randomly selecting a cheesecake Express your answer as a fraction decimal and percent H What is the probability of a person randomly selecting an apple pie putting it back and then selecting a cookie Express your answer as a fraction decimal and percent What is the probability of a person randomly selecting a cheesecake eating it and then selecting an apple pie Express your answer as a fraction decimal and percent 3 more coin flin

Statistics
Probabilityspaces Ex 123 45 Question 47 2 points Listen two decimal places and include the No Nancy invests 10 000 at 8 per year compounded semi annually Determine the amount after 5 years Compount Interest Formula A P 1 i Round final answer to the nearest cent 2 decimal places
Statistics
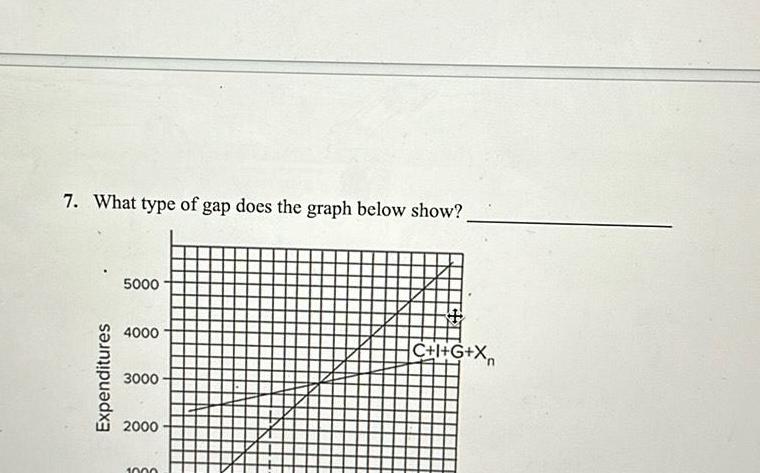
Statistics7 What type of gap does the graph below show Expenditures 5000 4000 3000 2000 1000 C I G X

Statistics
StatisticsSamuel performed a linear regression using the following data X 4 5 7 5 10 12 2 13 16 18 Y 0 4 0 9 3 0 6 4 10 5 12 2 19 7 25 7 If excel generated the following line of best fit y 1 8x 9 4 find the value of the residual for the x value of 16 Give your answer correct to two decimal places Your Answer
Statistics
ProbabilityFalse ideas about race have been used to justify check your answer in Section 2 O The study of people without regard for their cultural beliefs or humanity O Colonialism and immigration policies O All of these things and more O Slave trade

Statistics
StatisticsWhat is the definition of biological evolution Check your answer in Section 1 O Population changes due to natural selection O Mutation due to norm of reaction O A change in allele frequencies in a population over time Change in an organism over its life span