Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
DifferentiationLet y tan 2x 5 Find the differential dy when z 5 and dz 0 4 0 8574 Find the differential dy when z 5 and da 0 8 1 7148

Calculus
DifferentiationGiven the piecewise function defined by 3 x if x 1 H x x 1 if 1 x 3 x 3 if x 3 What is the value of H 3 H 3 OA 4 OB 6 OC 10 OR None of the above

Calculus
Differentiationhatch the functions with their graphs Enter the letter of the graph below which corresponds to the function Click on image for a larger view OD A OD 1 y 2 sin r 2 y 1 cos x 3 y cos 4 y 1 sin a NE B C D
Calculus
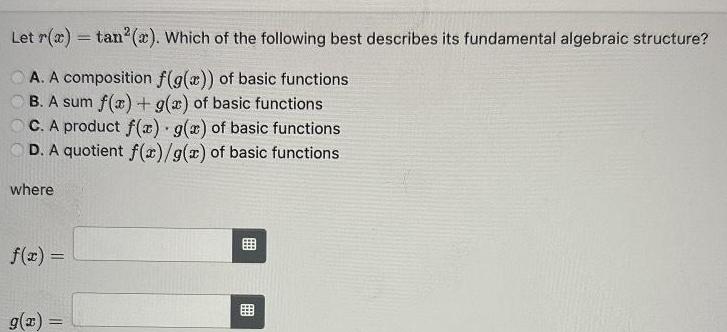
Differential equationsLet r x tan x Which of the following best describes its fundamental algebraic structure A A composition f g x of basic functions B A sum f x g x of basic functions C A product f x g x of basic functions D A quotient f x g x of basic functions where f x g x B
Calculus
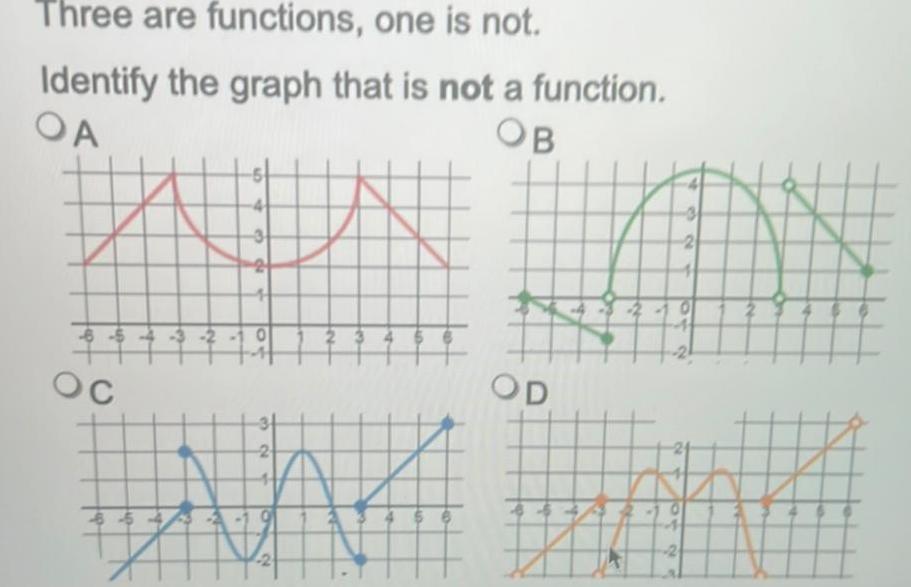
Application of derivativesThree are functions one is not Identify the graph that is not a function OB OA OC 654 3 di N 3 2 2 OD N O




Calculus
Application of derivativesomework A cave with beautiful prehistoric wall paintings was discovered Some charcoal found in the cave contained 15 of the constant for 14C is 00012 The cave paintings are years old Round to the nearest year as needed Points 0 OT 14 C expected in living trees How old are the cave paintings The decay
Calculus
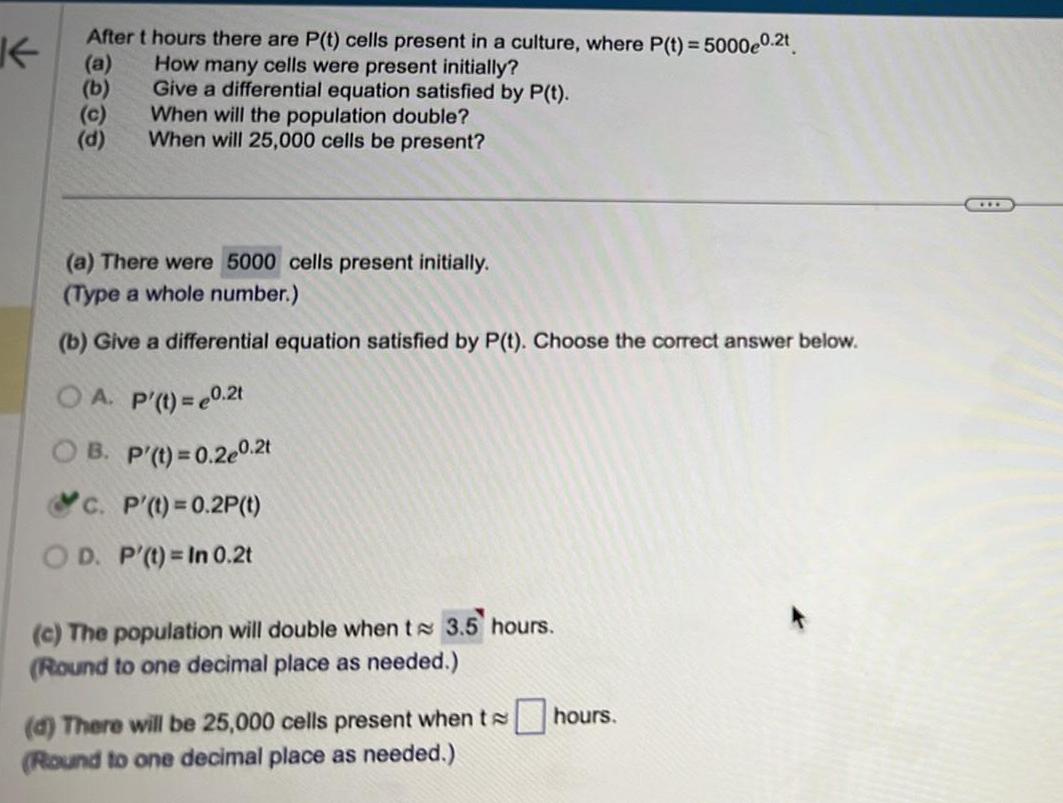
Differential equationsK After t hours there are P t cells present in a culture where P t 5000e0 2t a How many cells were present initially Give a differential equation satisfied by P t When will the population double When will 25 000 cells be present c d a There were 5000 cells present initially Type a whole number b Give a differential equation satisfied by P t Choose the correct answer below OA P t 0 2t B P t 0 2e0 2t c P t 0 2P t OD P t In 0 2t c The population will double when te 3 5 hours Round to one decimal place as needed d There will be 25 000 cells present when thours Round to one decimal place as needed
Calculus
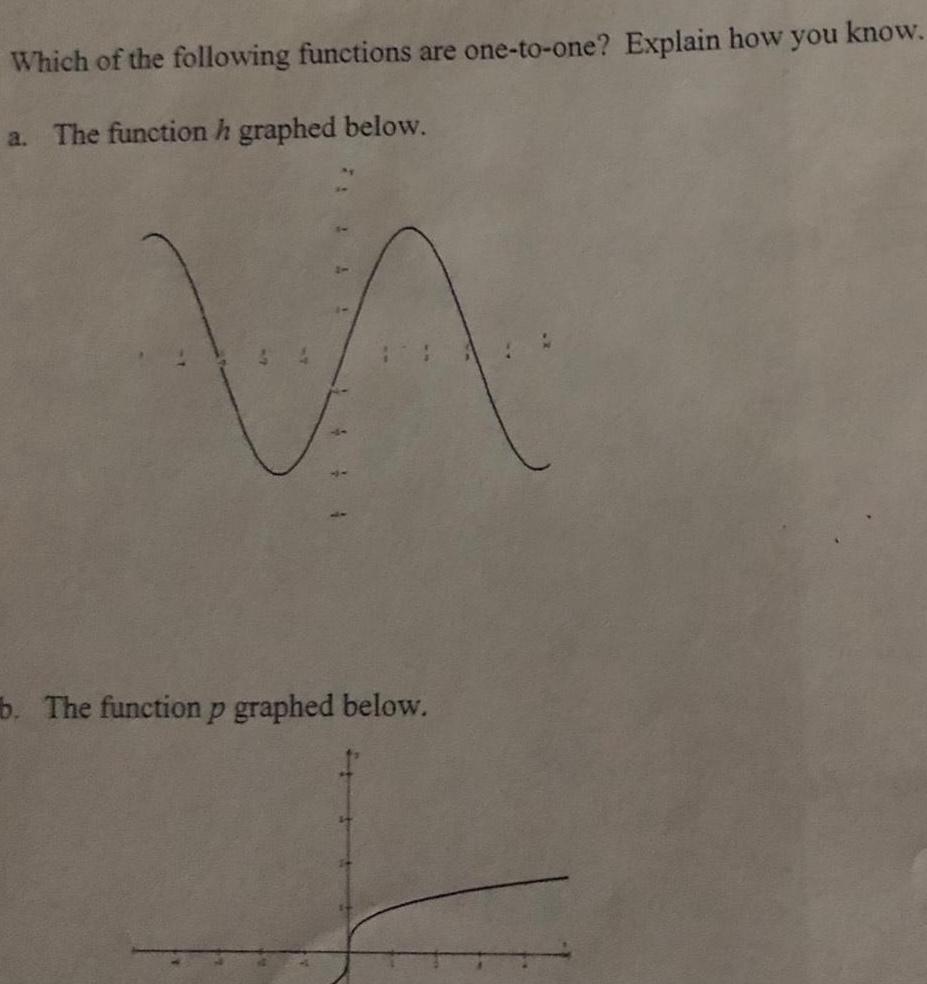
DifferentiationWhich of the following functions are one to one Explain how you know a The function h graphed below b The function p graphed below
Calculus
Application of derivativesa Find the formula for P t P t 12e 0 027t Type an expression using t as the variable b What is P 0 P 0 12 c What is the decay constant Part 3 of 9 A sample of 12 grams of radioactive material is placed in a vault Let P t be the amount remaining after t years and let P t satisfy the differential equation P t 0 027P t Answer parts through g C Points 0 of 1
Calculus
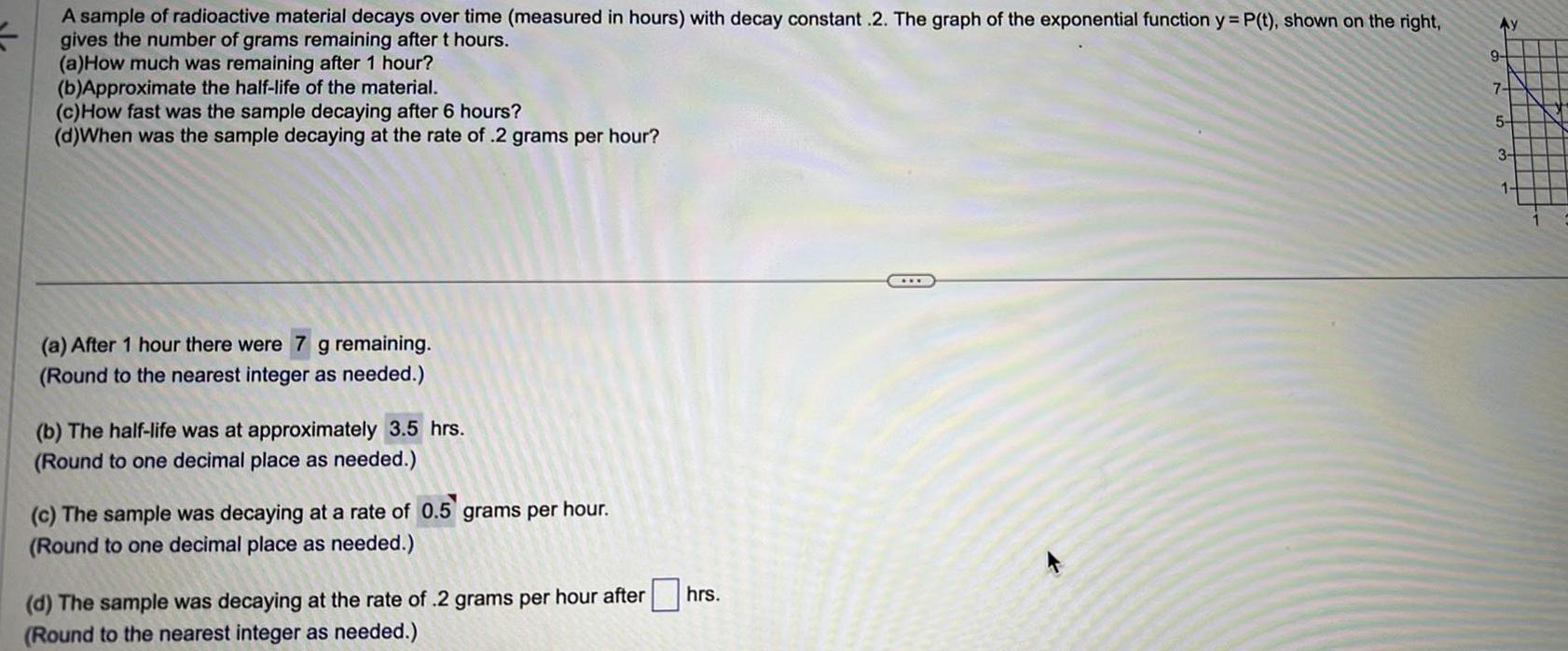
Application of derivativesA sample of radioactive material decays over time measured in hours with decay constant 2 The graph of the exponential function y P t shown on the right 5 gives the number of grams remaining after t hours a How much was remaining after 1 hour b Approximate the half life of the material c How fast was the sample decaying after 6 hours d When was the sample decaying at the rate of 2 grams per hour a After 1 hour there were 7 g remaining Round to the nearest integer as needed b The half life at approximately 3 5 hrs Round to one decimal place as needed c The sample was decaying at a rate of 0 5 grams per hour Round to one decimal place as needed d The sample was decaying at the rate of 2 grams per hour after Round to the nearest integer as needed hrs Ay 9 7 5 3 1
Calculus
DifferentiationPart 1 of 9 a Find the formula for P t P t Type an expression using t as the variable Points 0 of 1 A sample of 12 grams of radioactive material is placed in a vault Let P t be the amount remaining after t years and let P t satisfy the differential equation P t 0 027P t Answer parts a through g
Calculus
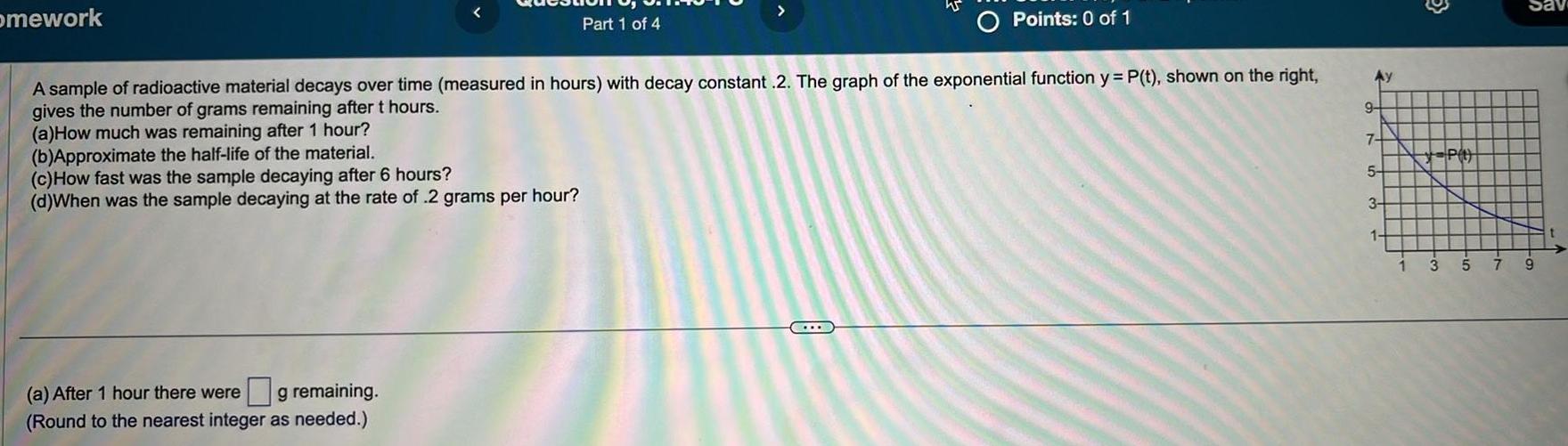
Differentiationmework c How fast was the sample decaying after 6 hours d When was the sample decaying at the rate of 2 grams per hour a After 1 hour there were g remaining Round to the nearest integer as needed Part 1 of 4 A sample of radioactive material decays over time measured in hours with decay constant 2 The graph of the exponential function y P t shown on the right gives the number of grams remaining after t hours a How much was remaining after 1 hour b Approximate the half life of the material O C Points 0 of 1 975 3 1 P 4 3 5 7 Sav 9
Calculus
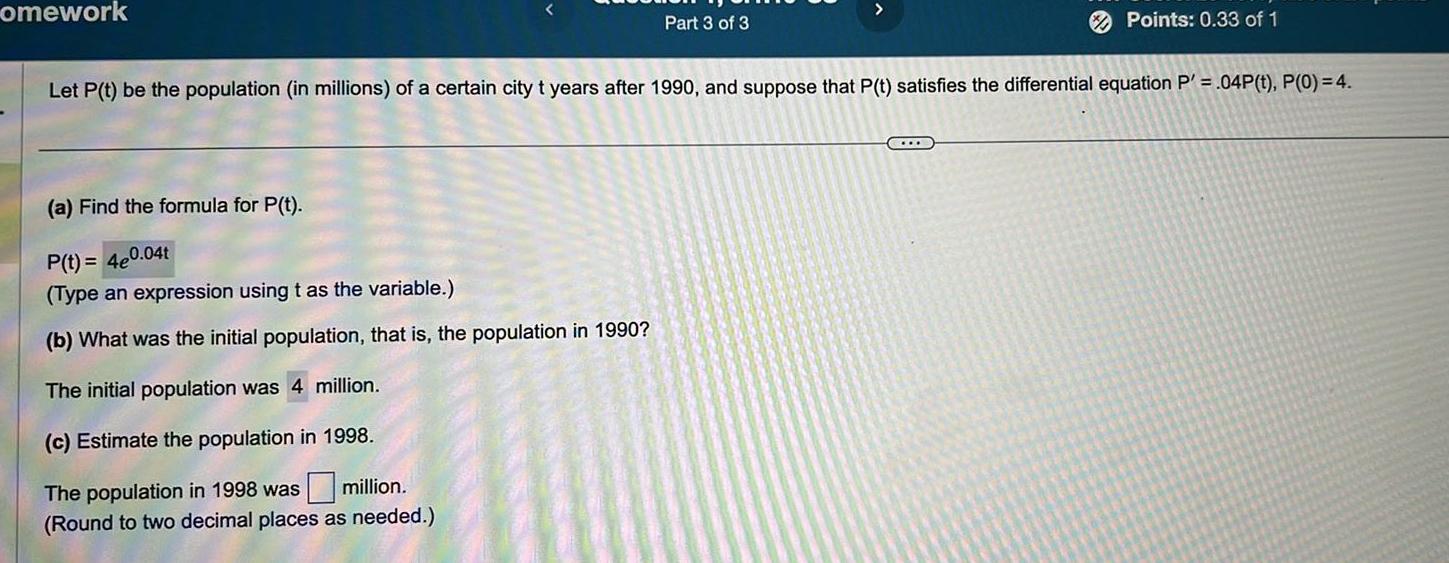
Differential equationsomework Part 3 of 3 a Find the formula for P t P t 4e0 04t Type an expression using t as the variable b What was the initial population that is the population in 1990 The initial population was 4 million c Estimate the population in 1998 The population in 1998 was million Round to two decimal places as needed Points 0 33 of 1 Let P t be the population in millions of a certain city t years after 1990 and suppose that P t satisfies the differential equation P 04P t P 0 4
Calculus
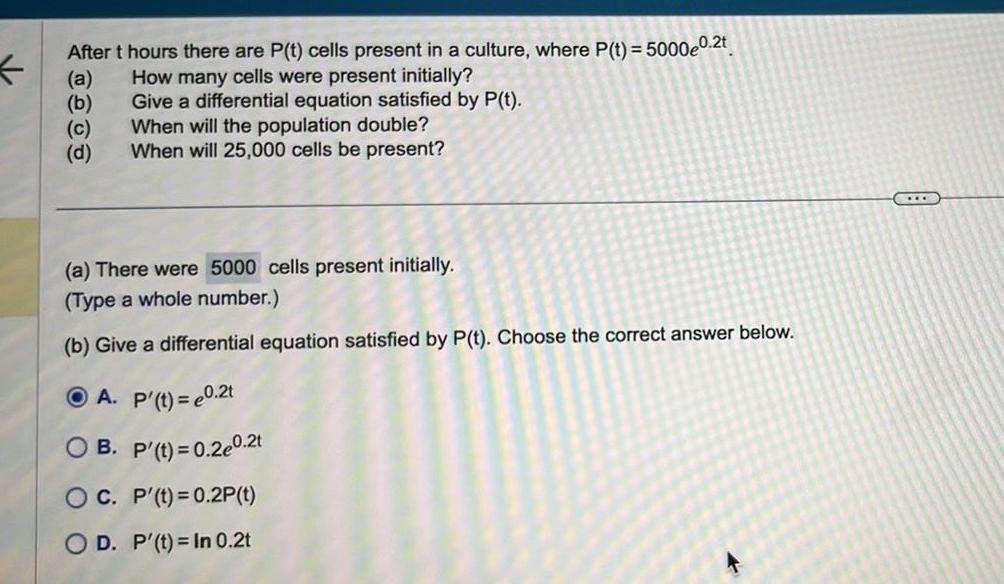
Differential equationsAfter t hours there are P t cells present in a culture where P t 5000e0 2t How many cells were present initially Give a differential equation satisfied by P t When will the population double When will 25 000 cells be present a b c d a There were 5000 cells present initially Type a whole number b Give a differential equation satisfied by P t Choose the correct answer below A P t 0 2t OB P t 0 2e0 2t OC P t 0 2P t OD P t In 0 2t

Calculus
Application of derivativesPoints 0 of 1 At the beginning of 1990 22 3 million people lived in the metropolitan area of a particular city and the population was growing exponentially The 1994 population was 27 million If this trend continues how large will the population be in the year 2009 The population will be million people Round to the nearest integer as needed
Calculus
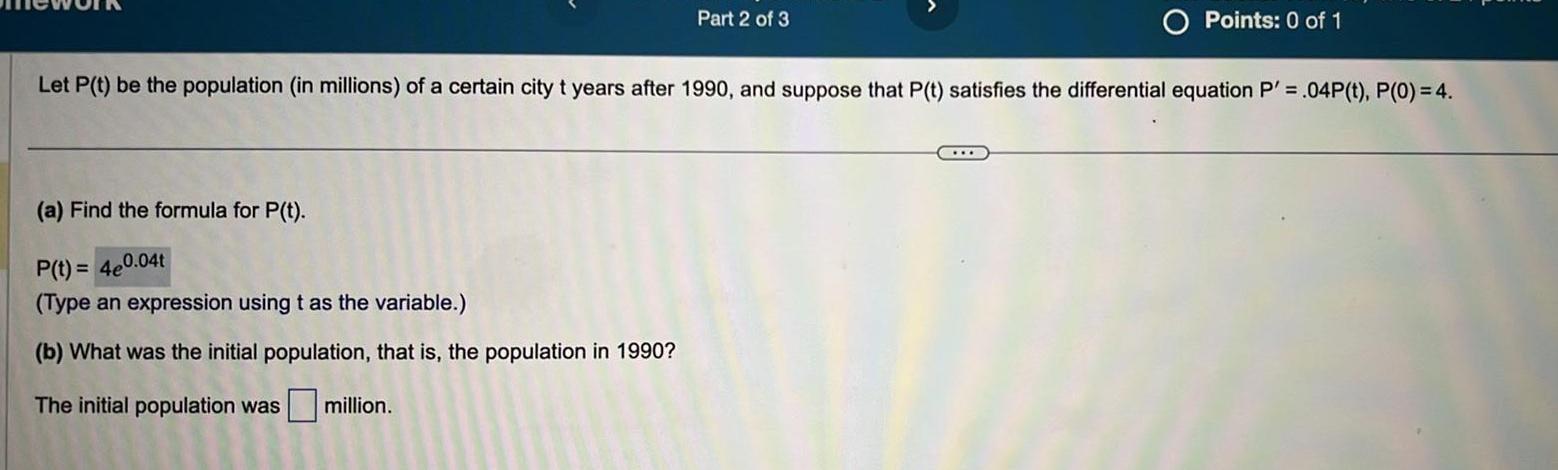
Application of derivativesPart 2 of 3 a Find the formula for P t P t 4e0 04t Type an expression using t as the variable b What was the initial population that is the population in 1990 The initial population was million Points 0 of 1 Let P t be the population in millions of a certain city t years after 1990 and suppose that P t satisfies the differential equation P 04P t P 0 4

Calculus
Vector CalculusPoints A company invests 20 000 in a CD that earns 9 compounded continuously How long will it take for the account to be worth 30 000 The account will be worth approximately 30 000 in about years Do not round until the final answer Then round to the nearest tenth as needed
Calculus
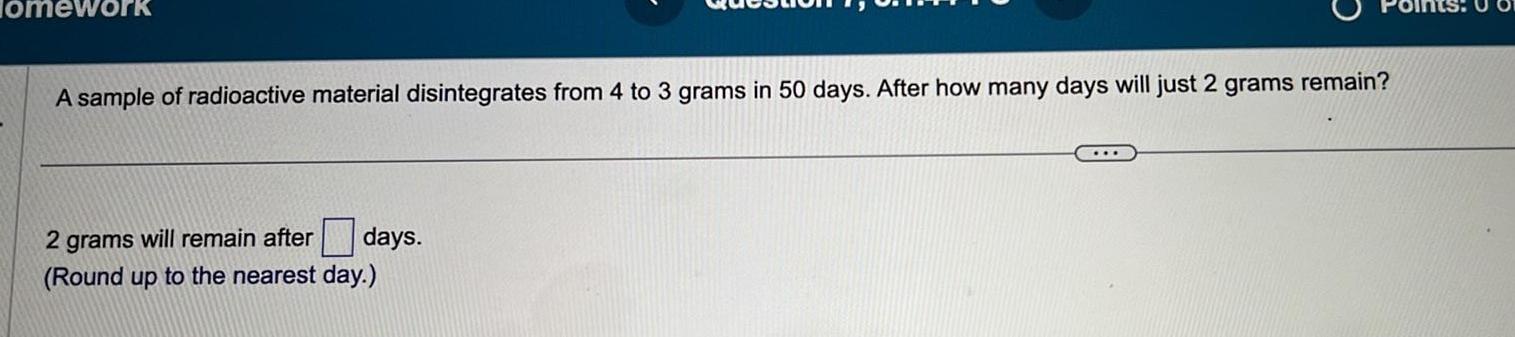
Application of derivativesHomework A sample of radioactive material disintegrates from 4 to 3 grams in 50 days After how many days will just 2 grams remain days 2 grams will remain after Round up to the nearest day
Calculus
Differential equationsFive thousand dollars is deposited into a savings account at 7 5 interest compounded continuously a What is the formula for A t the balance after t years b What differential equation is satisfied by A t the balance after t years c How much money will be in the account after 5 years d When will the balance reach 8000 e How fast is the balance growing when it reaches 8000 a A t

Calculus
Vector CalculusWhen time is measured in days the decay constant for a particular radioactive isotope is 0 14 Determine the time required for a confined sample of the isotope to fall to 80 of its original value The time required for a confined sample of the isotope to fall to 80 of its original value is about Do not round until the final answer Then round to the nearest hundredth as needed days
Calculus
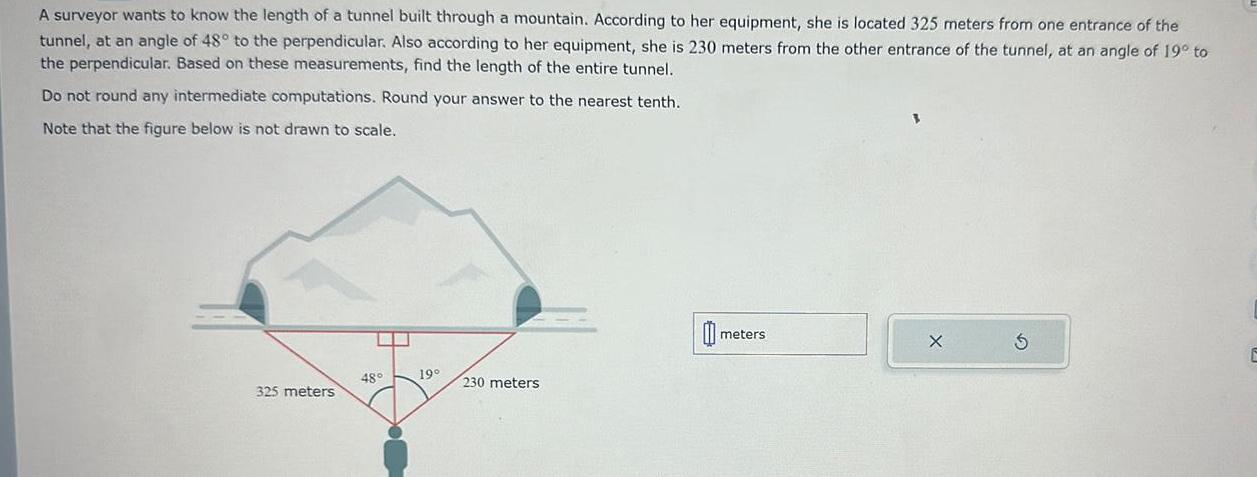
Application of derivativesA surveyor wants to know the length of a tunnel built through a mountain According to her equipment she is located 325 meters from one entrance of the tunnel at an angle of 48 to the perpendicular Also according to her equipment she is 230 meters from the other entrance of the tunnel at an angle of 19 to the perpendicular Based on these measurements find the length of the entire tunnel Do not round any intermediate computations Round your answer to the nearest tenth Note that the figure below is not drawn to scale 325 meters 48 19 230 meters 0 meters E
Calculus
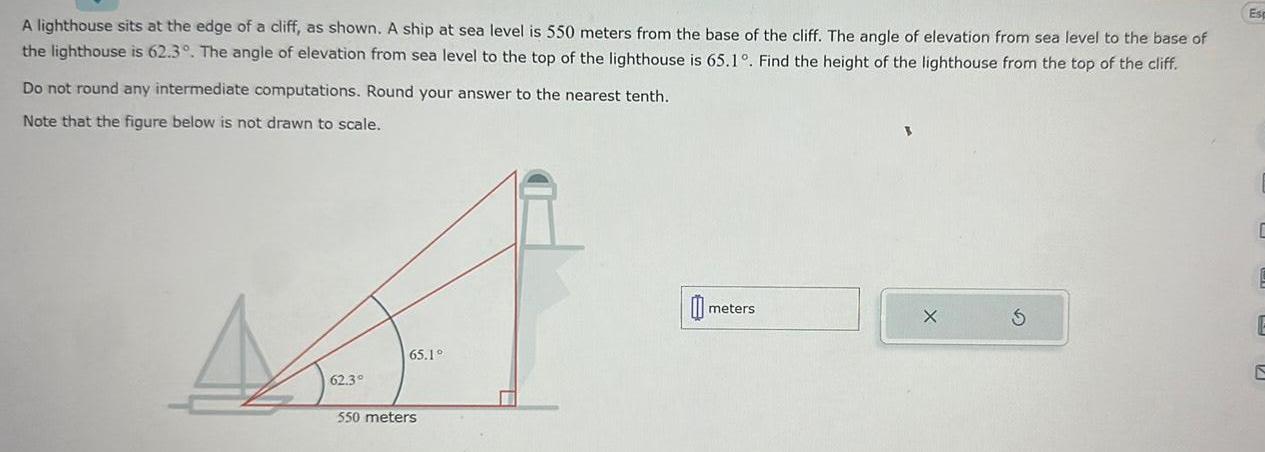
Application of derivativesA lighthouse sits at the edge of a cliff as shown A ship at sea level is 550 meters from the base of the cliff The angle of elevation from sea level to the base of the lighthouse is 62 3 The angle of elevation from sea level to the top of the lighthouse is 65 1 Find the height of the lighthouse from the top of the cliff Do not round any intermediate computations Round your answer to the nearest tenth Note that the figure below is not drawn to scale 62 3 65 1 550 meters 0 meters Es C E E
Calculus
Definite IntegralsHomework Part 1 of 3 a Find the formula for P t P t Type an expression using t as the variable Points 0 of 1 Let P t be the population in millions of a certain city t years after 1990 and suppose that P t satisfies the differential equation P 04P t P 0 4
Calculus
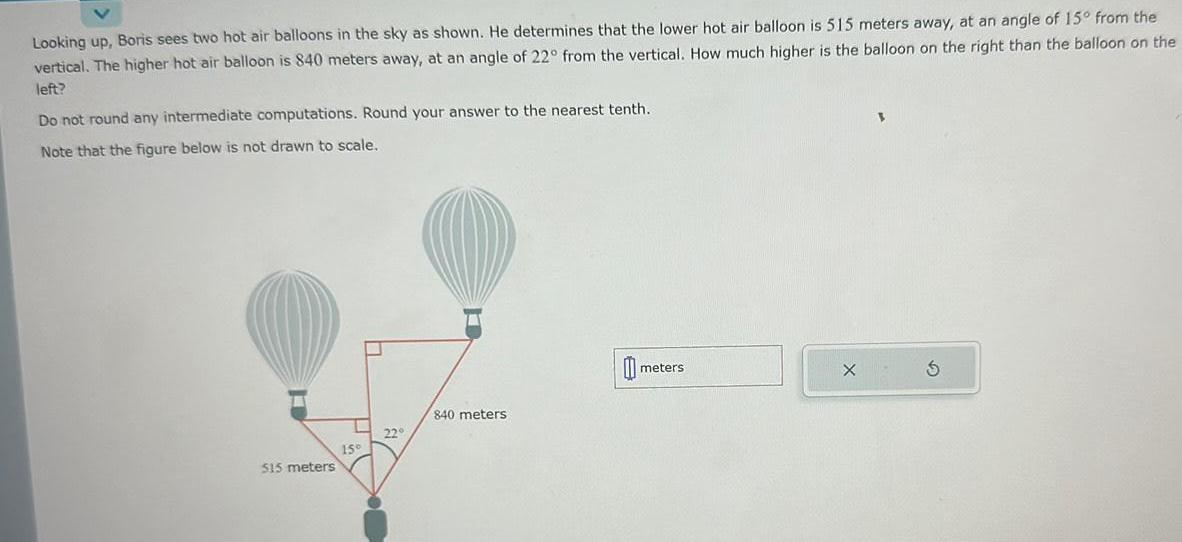
DifferentiationLooking up Boris sees two hot air balloons in the sky as shown He determines that the lower hot air balloon is 515 meters away at an angle of 15 from the vertical The higher hot air balloon is 840 meters away at an angle of 22 from the vertical How much higher is the balloon on the right than the balloon on the left Do not round any intermediate computations Round your answer to the nearest tenth Note that the figure below is not drawn to scale 515 meters 15 22 840 meters meters X
Calculus
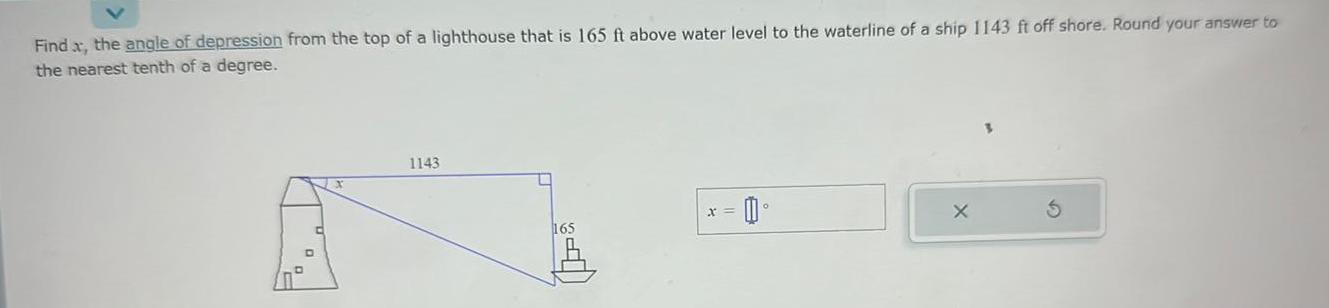
DifferentiationFind x the angle of depression from the top of a lighthouse that is 165 ft above water level to the waterline of a ship 1143 ft off shore Round your answer to the nearest tenth of a degree 1143 U 165 0 x X

Calculus
DifferentiationA ramp 22 ft long rises to a platform The bottom of the platform is 13 ft from the foot of the ramp Find x the angle of elevation of the ramp Round your answer to the nearest tenth of a degree Xx 13 Platform Ground X

Calculus
Application of derivativesRewrite the following expression in terms of exponentials and simplify the result as much as you can 5 sinh 5 In x 5 sinh 5 Inx Simplify your answer Use integers or fractions for any numbers in the expression Do not factor

Calculus
DifferentiationA 12 ft ladder leans against the side of a house The top of the ladder is 10 ft off the ground Find x the angle of elevation of the ladder Round your answer to the nearest tenth of a degree 10 12 0 x

Calculus
Vector Calculusplane is 120 mi north and 194 mi east of an airport Find x the angle the pilot should turn in order to fly directly to the airport Round your answer to the earest tenth of a degree 120 U Airport 194 X


Calculus
Application of derivatives3 sinh 2 In x Simplify your answer Use integers or fractions for any numbers in the expression D
Calculus
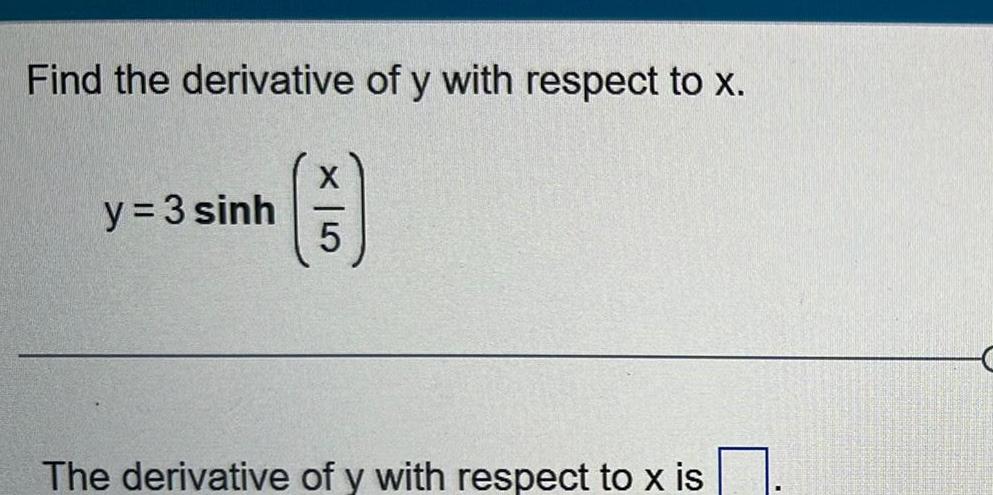
Application of derivativesFind the derivative of y with respect to x F 5 y 3 sinh The derivative of y with respect to x is

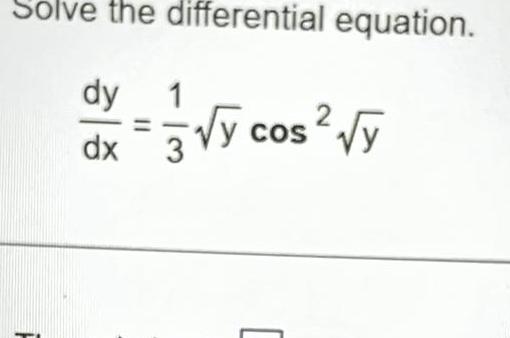
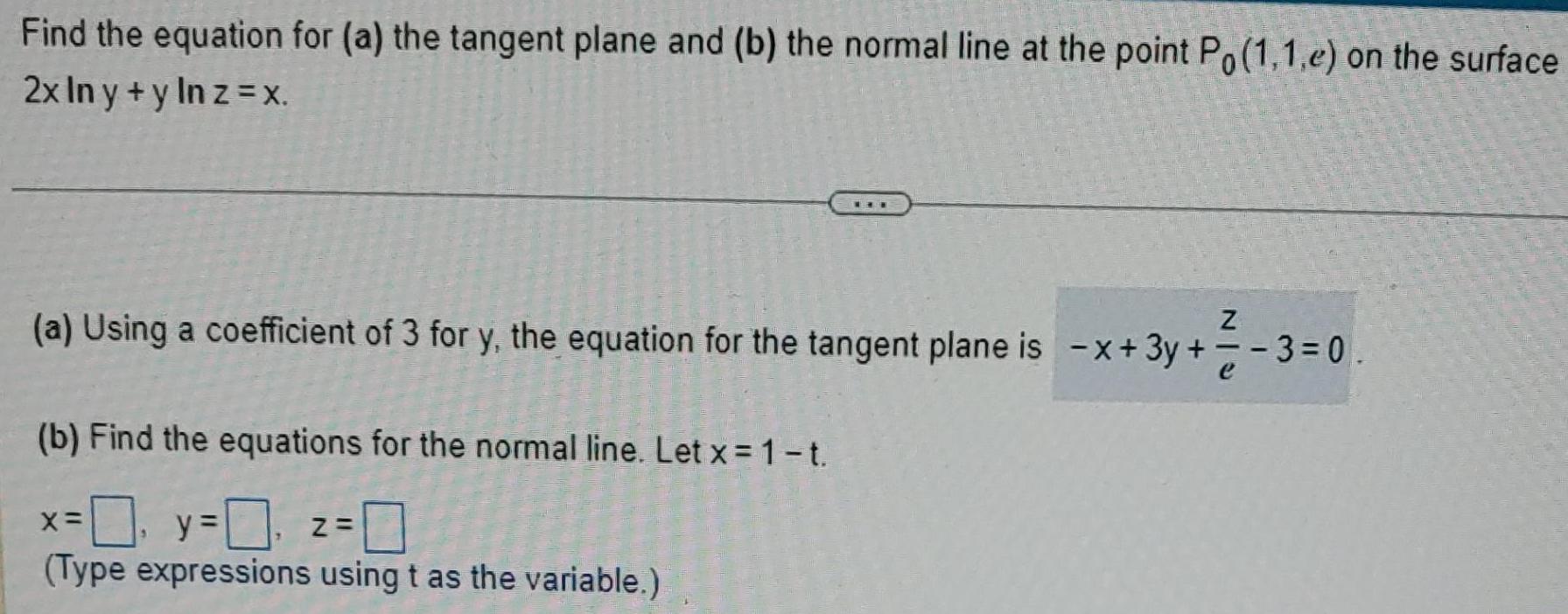
Calculus
Application of derivativesFind the equation for a the tangent plane and b the normal line at the point Po 1 1 e on the surface 2x ln y y ln z X Z a Using a coefficient of 3 for y the equation for the tangent plane is x 3y b Find the equations for the normal line Let x 1 t 0 y 0 z 0 Type expressions using t as the variable X 3 0

Calculus
Differential equationsdL The intensity L x of light x feet beneath the surface of the ocean satisfies the differential equation dx From experience a diver knows that diving to 19 ft in a sea cuts the intensity in half He cannot work without artificial light when the intensity falls below one tenth of the surface value About how deep can he expect to work without artificial light He can work approximately ft deep without artificial light Simplify your answer Round to the nearest tenth as needed KL
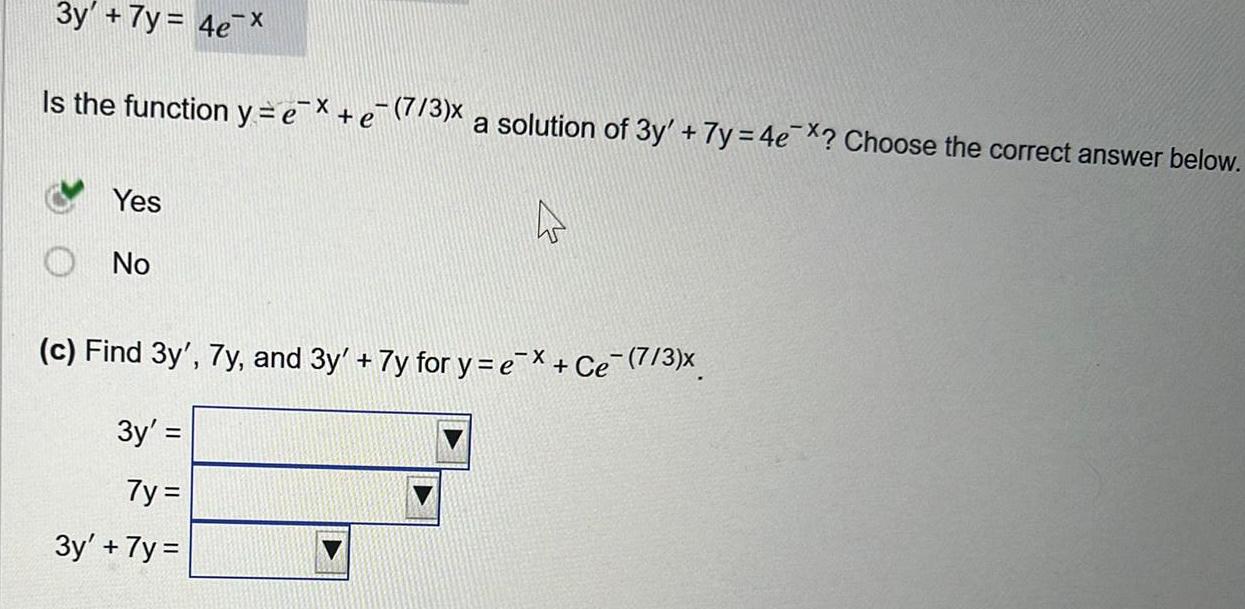
Calculus
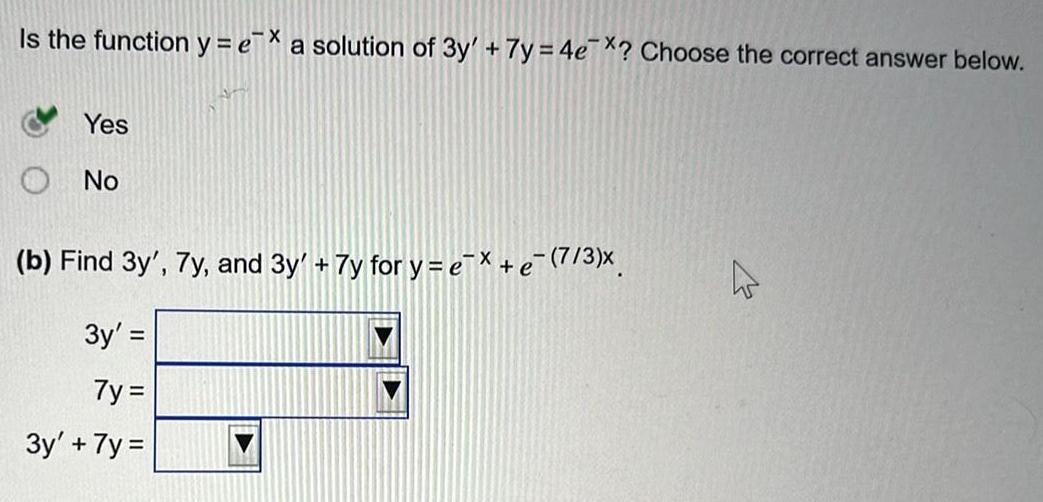
Differential equations3y 7y 4e X Is the function y e Yes No 7 3 x a solution of 3y 7y 4e Choose the correct answer below 4 c Find 3y 7y and 3y 7y for y e e 7 3 3y 7y 3y 7y
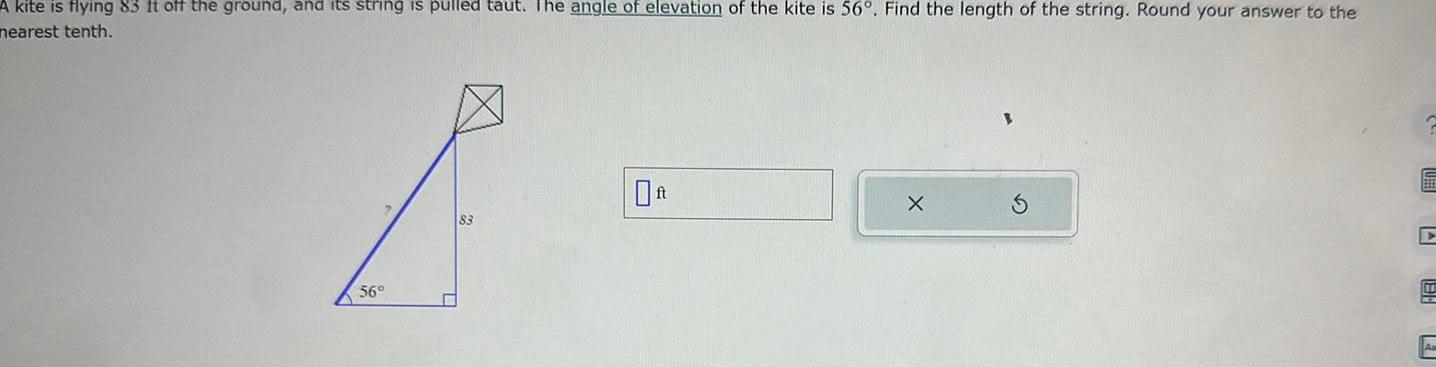
Calculus
Differential equationsA kite is flying 83 ft off the ground and its string is pulled taut The angle of elevation of the kite is 56 Find the length of the string Round your answer to the nearest tenth 56 83 X S HB P
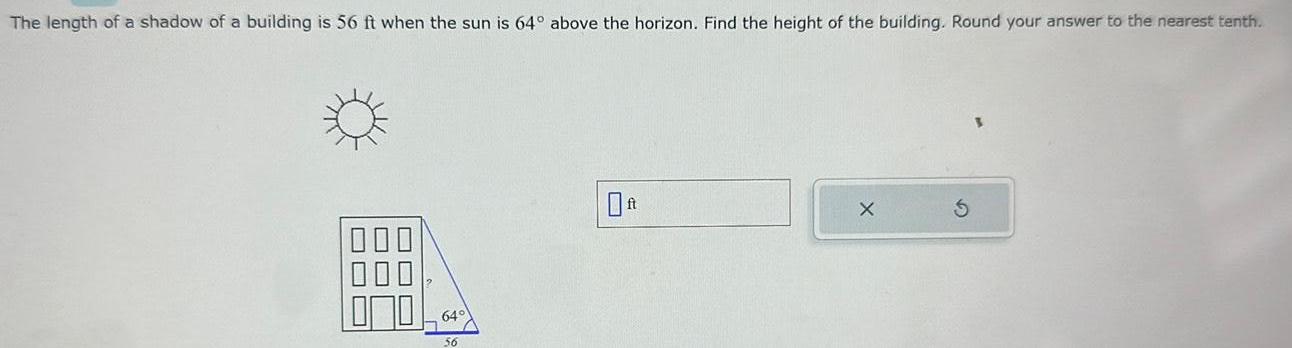
Calculus
DifferentiationThe length of a shadow of a building is 56 ft when the sun is 64 above the horizon Find the height of the building Round your answer to the nearest tenth 000 56 X
Calculus
DifferentiationIs the function y ex a solution of 3y 7y 4e X Choose the correct answer below Yes No Batt b Find 3y 7y and 3y 7y for y e x e 7 3 3y 7y 3y 7y

Calculus
Application of derivativesSuppose that the bacteria in a colony grow unchecked according to the Law of Exponential Change The colony starts with 1 bacterium and triples in number every 30 minutes How many bacteria will the colony contain at the end of 24 hours At the end of 24 hours the colony will contain bacteria Use scientific notation Use the multiplication symbol in the math palette as needed Round to one decimal place as needed
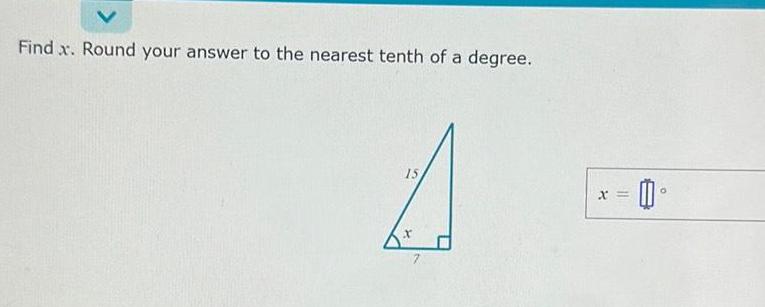

Calculus
Differential equationsSolve the differential equation dy dx 11 1 2 y cos y COS The solution is
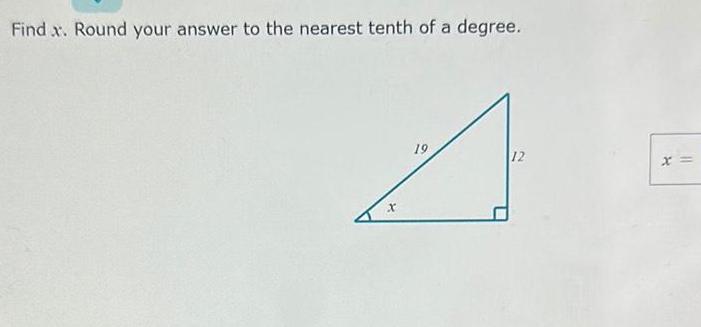
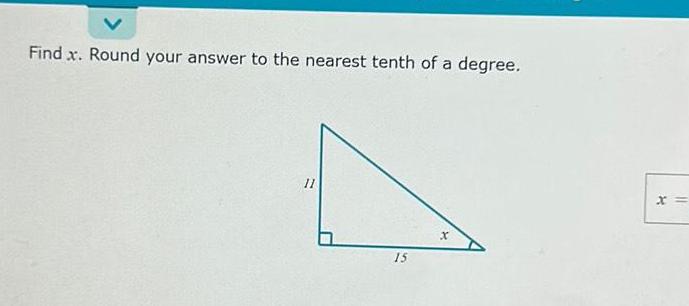
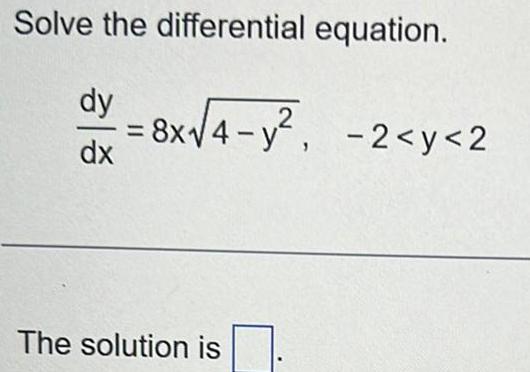

Calculus
Differential equationsCheck whether each of the following functions is a solution of the differential equation 3y 7y 4e x X b y e e 7 3 x a y ex c y ex Ce 7 3 x a Find 3y 7y and 3y 7y for y ex 3y 7y 3y 7y