Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
Definite Integralsfoculista doctor who examines and treats people s eyes 12 A Letter to Teach through Project Utkarsh ne that you are Balvir Bairagi a student of class XI of Gout Senior Secondary Scho letter to the principal of your school requesting him to teach your class through Shanti Sadan Baseri 23 October 20 The Principal Govt Senior Secondary School Baseri of scholarsh to know unt I questes bmitt best reg obedie Verm Yesterday I got myself registered as a student and found that it would be very helpful for us in improving our division and the result of our school if we were taught through it I hope that you will personally look into the matter and make necessary arrangement for it With best regards Yours obediently Balvir Bairagi 13 Non deposit of Scholarshin XC ter Ne A Lett et cho Subject Teaching through project Utkarsh Sir With due respect I wish to state that I am a student of class XI B Almost all the teachers of Rom our school are highly talented and qualified There is no doubt that they teach us excellently They are truly devoted to us They are keen in solving our problems But no teacher teaches us through Project Utkarsh instgar Octob The Prin vt Se abject

Calculus
Application of derivativesClassification of phy srics of fat stoffaszeg Physics Classical physics PRIN A Kma 3 modem physic A

Calculus
Application of derivativesin calculus than the other lo functions y logb x 2 26 Differentiate the function 2 g t In 3 1

Calculus
Definite IntegralsThe area of the region bounded by the curve y x the lines x 1 and x 4 and the x axis is the area ABCD Class XII Chapter 8 Application of Integrals Maths Area of ABCD ydx xdx 11 14 3 units

Calculus
Definite IntegralsAnswer The area of the region bounded by the curve x 4y y 2 and y 4 and the y axis is the area ABCD Class XII Chapter 8 Application of Integrals Maths Area of ABCD xdy 2 ydy 2 ydy 1 Page 4 of 53

Calculus
Application of derivatives126 Homework 7 Sect 2 6 ts A function g is given In parts a and b start with a standard function f and show the ic steps for transforming the graph of f into the graph of g Also describe each transformation s In parts c and d just describe the transformation steps in words x 2 x 0 5 x 2 1 g x 4 f 3x
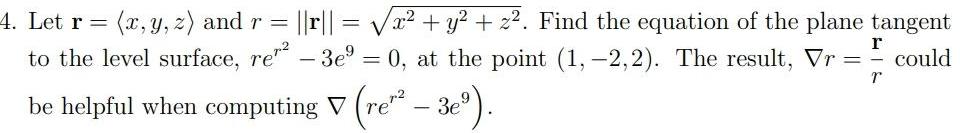
Calculus
Definite Integrals4 Let r x y z and r r x y z Find the equation of the plane tangent to the level surface re 3e 0 at the point 1 2 2 The result Vr r could be helpful when computing V re2 3e r

Calculus
Application of derivativesFind equations for the tangent plane and the normal line at point Po XoYo Zo 2 5 0 on the surfa 6 cos xx 6x y 2x yz 116 Using a coefficient of 40 for x the equation for the tangent plane is
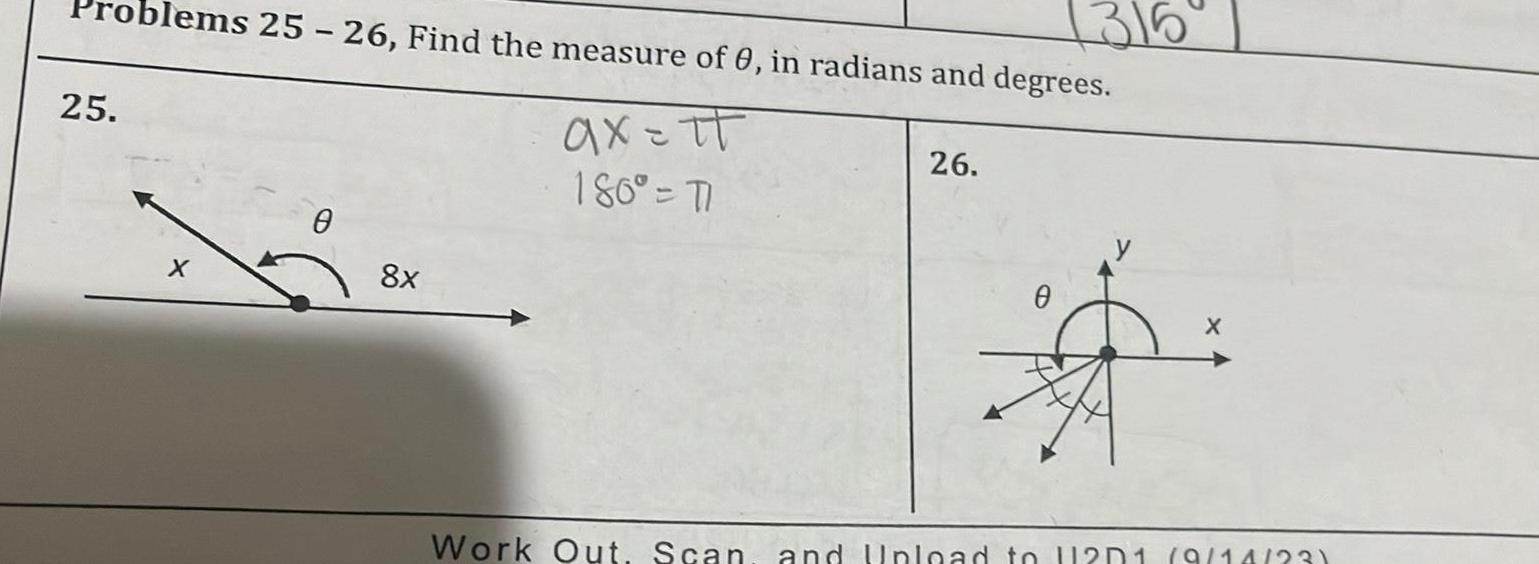
Calculus
Application of derivatives25 blems 25 26 Find the measure of 0 in radians and degrees ax tt 180 TI X 8x 26 0 X Work Out Scan and Upload to 12D1 9 14 23


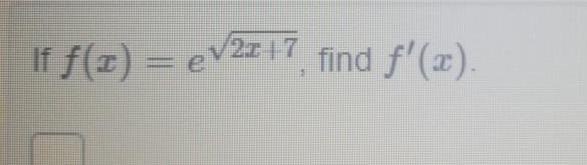
Calculus
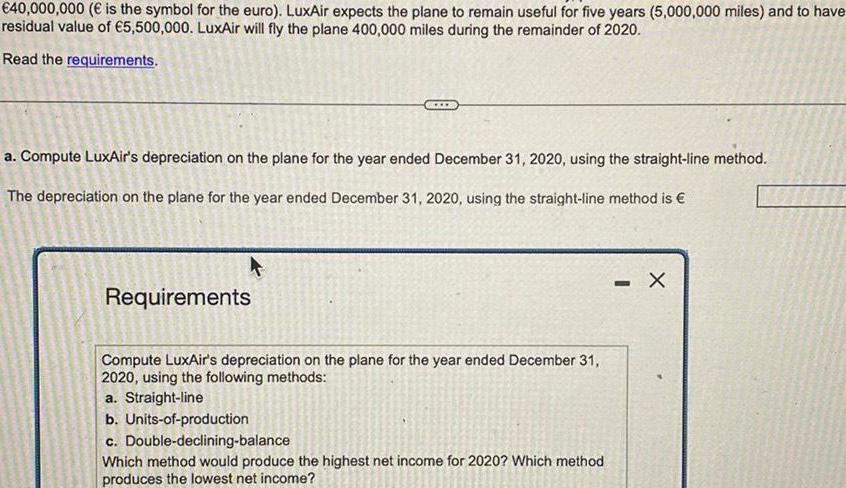
Application of derivatives40 000 000 is the symbol for the euro LuxAir expects the plane to remain useful for five years 5 000 000 miles and to have residual value of 5 500 000 LuxAir will fly the plane 400 000 miles during the remainder of 2020 Read the requirements a Compute LuxAir s depreciation on the plane for the year ended December 31 2020 using the straight line method The depreciation on the plane for the year ended December 31 2020 using the straight line method is Requirements Compute LuxAir s depreciation on the plane for the year ended December 31 2020 using the following methods a Straight line b Units of production c Double declining balance Which method would produce the highest net income for 2020 Which method produces the lowest net income X

Calculus
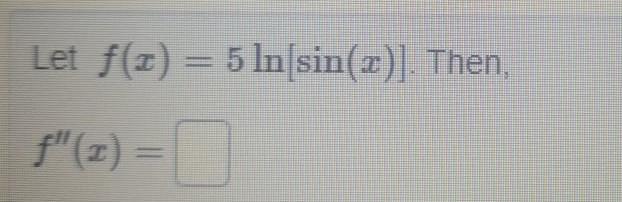
DifferentiationLet f x 6 ln sec z tan z HINT Simplify the first derivative before you find the second derivative

Calculus
Application of derivativesRewrite the expression as an algebraic expresion in 1 tan sin 2 Note by algebraic we mean that the answer is not allowed to use trig functions or inverse trig functions It is allowed to involve poly quotients and roots
Calculus
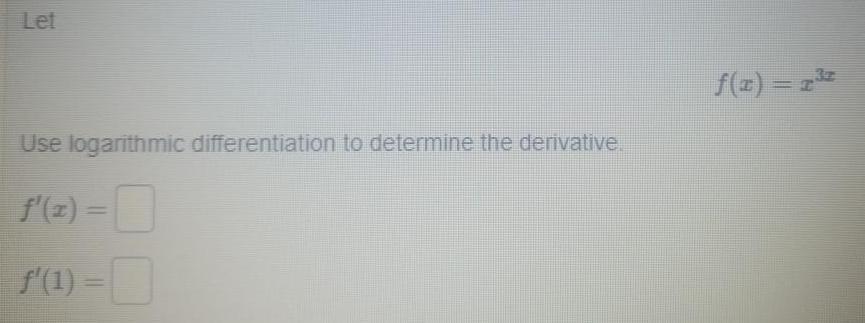
Differential equationsLet Use logarithmic differentiation to determine the derivative f x 1 f x 2

Calculus
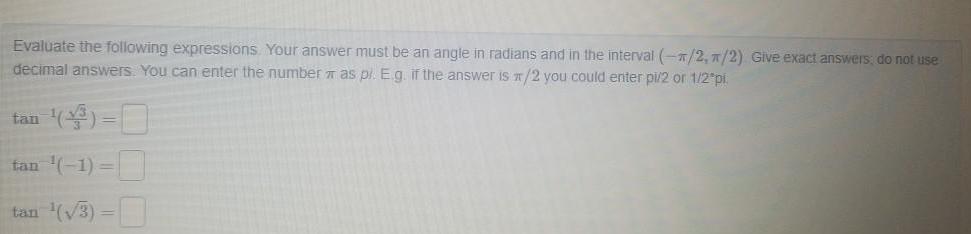
Application of derivativesEvaluate the following expressions Your answer must be an angle in radians and in the interval 1 2 1 2 Give exact answers do not use decimal answers You can enter the number as pi E g if the answer is x 2 you could enter pi 2 or 1 2 pi 3 tan 1 tan 3 tan 0
Calculus
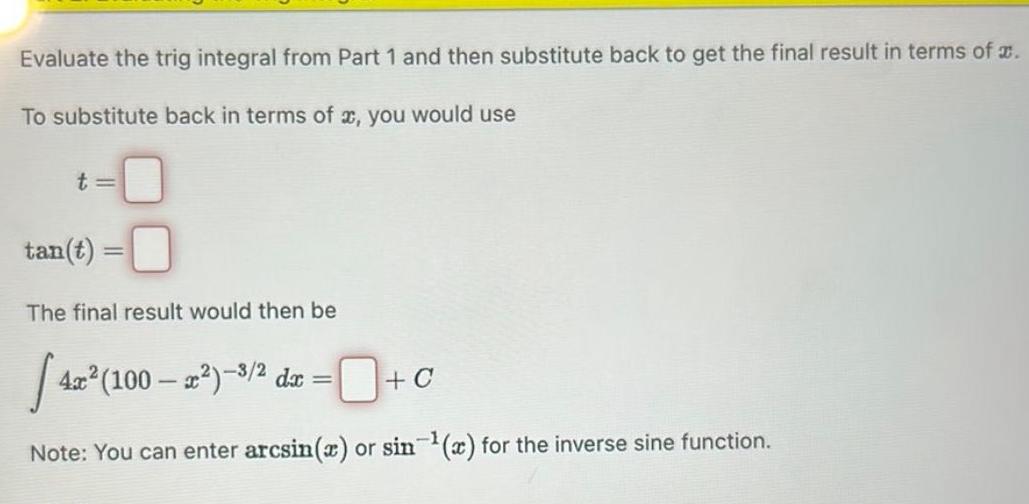
Indefinite IntegrationEvaluate the trig integral from Part 1 and then substitute back to get the final result in terms of To substitute back in terms of x you would use t tan t The final result would then be 42 4x 100 x 3 2 dx C Note You can enter arcsin x or sin x for the inverse sine function







Calculus
Definite Integralsa unique perspective of investme Forex Trading Platform JE 34 H 10 30 314 313 fafrius 3Thise th Fions 3 al da fa d az H 100 Safe and Secure Platform Best Opportunity in India fund com
Calculus
Definite IntegralsPOT 145 89 list 82 83 119 BJ 42 Specialist 05 8 12 P95 139 91 81 2 2015 2012 AC wh 85 0 RS XIMU 129 BS ANIMA 1 Vildande so 2 ap 3 cap Belacap Thuo 4 de Nimforex P Carbamed x 100 XIM 1 2 Vildamae 50 000 cap carbamed p 1 Is wounide M 2 cup carbamed actrl Don plod o

Calculus
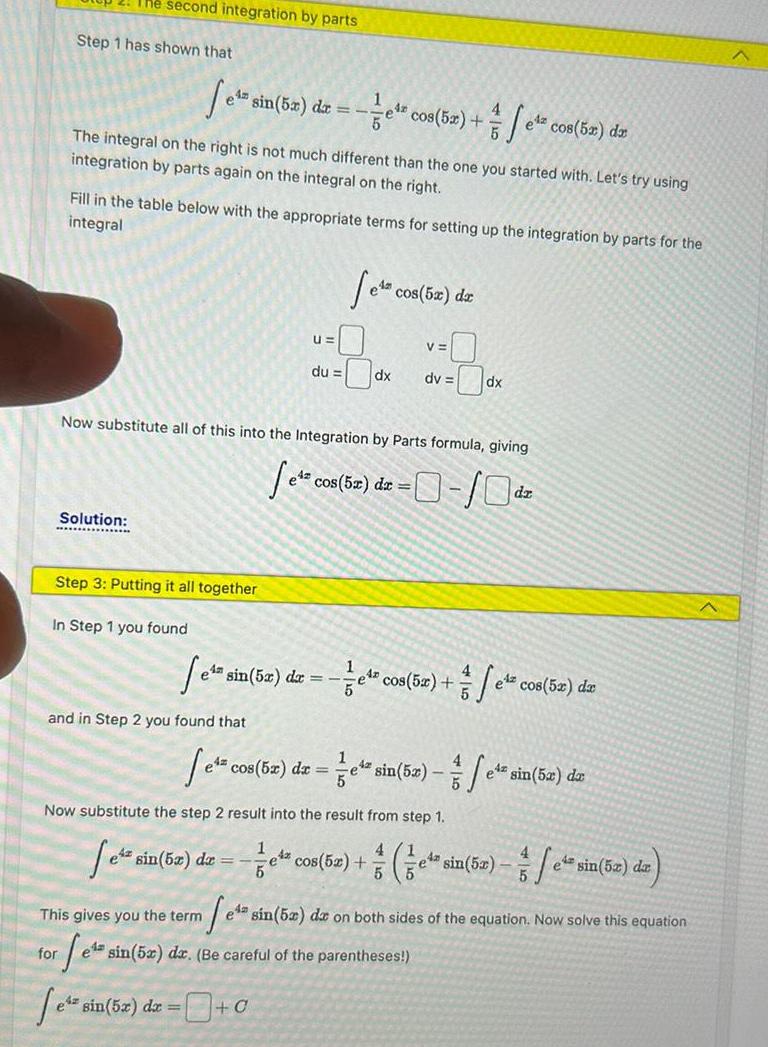
Indefinite Integration2 The second integration by parts Step 1 has shown that 1 4 e s sin 5x dx e cos 5x The integral on the right is not much different than the one you started with Let s try using integration by parts again on the integral on the right Solution Fill in the table below with the appropriate terms for setting up the integration by parts for the integral Step 3 Putting it all together In Step 1 you found and in Step 2 you found that U du ez sin 5x dx 1 5 e s cos 5x da 0 Now substitute all of this into the Integration by Parts formula giving e cos 5x dx 0 10 dx V 1 fe co dv dx e sin 5x dx e cos 5x fe el cos 5x dx cos 5x dx e cos bx dx e sin 52 e sin 52 da 5 Now substitute the step 2 result into the result from step 1 4 Setz 42 cos 52 e sin 5x fe 5 5 e sin 5x da This gives you the term e sin 52 dar on both sides of the equation Now solve this equation fets sin 52 dz Be careful of the parentheses for e sin 5x dx 0

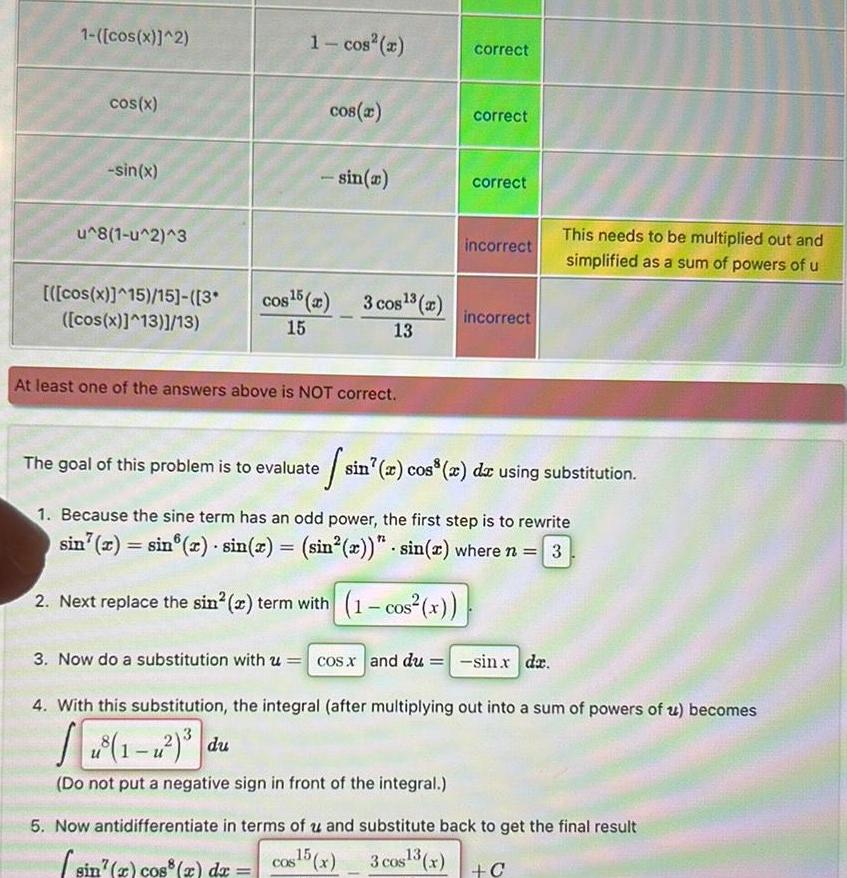
Calculus
Indefinite Integration1 cos x 2 cos x sin x u 8 1 u 2 3 cos x 15 15 3 cos x 13 13 1 cos cos x sin x cos 5 2 3 cos 2 15 13 At least one of the answers above is NOT correct correct correct correct incorrect incorrect The goal of this problem is to evaluate sin x cos x dx using substitution 1 Because the sine term has an odd power the first step is to rewrite sin x sin x sin x sin x sin x where n 3 2 Next replace the sin 2 term with 1 cos x This needs to be multiplied out and simplified as a sum of powers of u 3 Now do a substitution with u cos x and du sin x dx 4 With this substitution the integral after multiplying out into a sum of powers of u becomes Do not put a negative sign in front of the integral 5 Now antidifferentiate in terms of u and substitute back to get the final result cos15 x 3 cos 3 x sin x cos x dx C
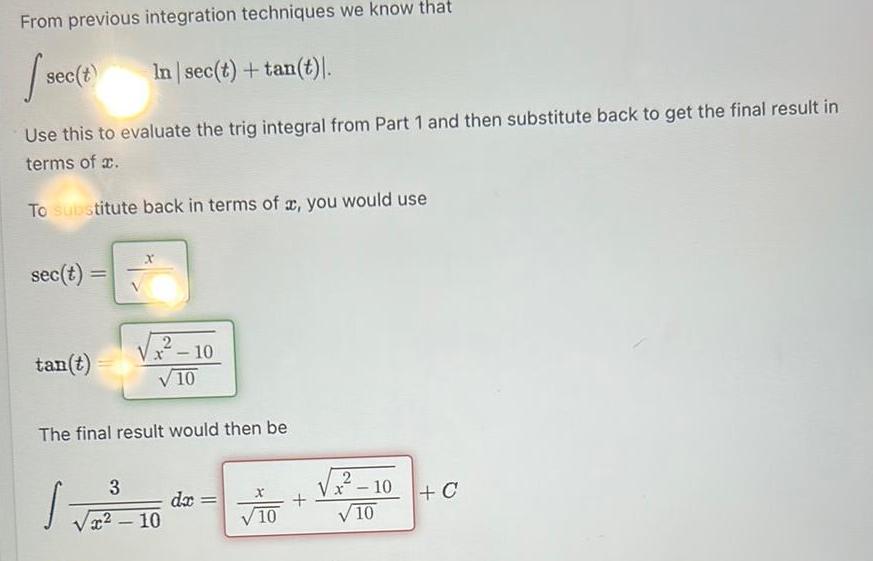
Calculus
Application of derivativesFrom previous integration techniques we know that sec t In sec t tan t Use this to evaluate the trig integral from Part 1 and then substitute back to get the final result in terms of To substitute back in terms of x you would use sec t tan t 2 x 10 10 The final result would then be 3 10 dx 10 2 Vx 10 10 C


Calculus
Application of derivativesFrom previous integration techniques we know that sec t dt In sec t tan t Use this to evaluate the trig integral from Part 1 and then substitute back to get the final result in terms of To substitute back in terms of x you would use tan t sec t The final result of the integration would then be 2 2 16 d 15 dx C
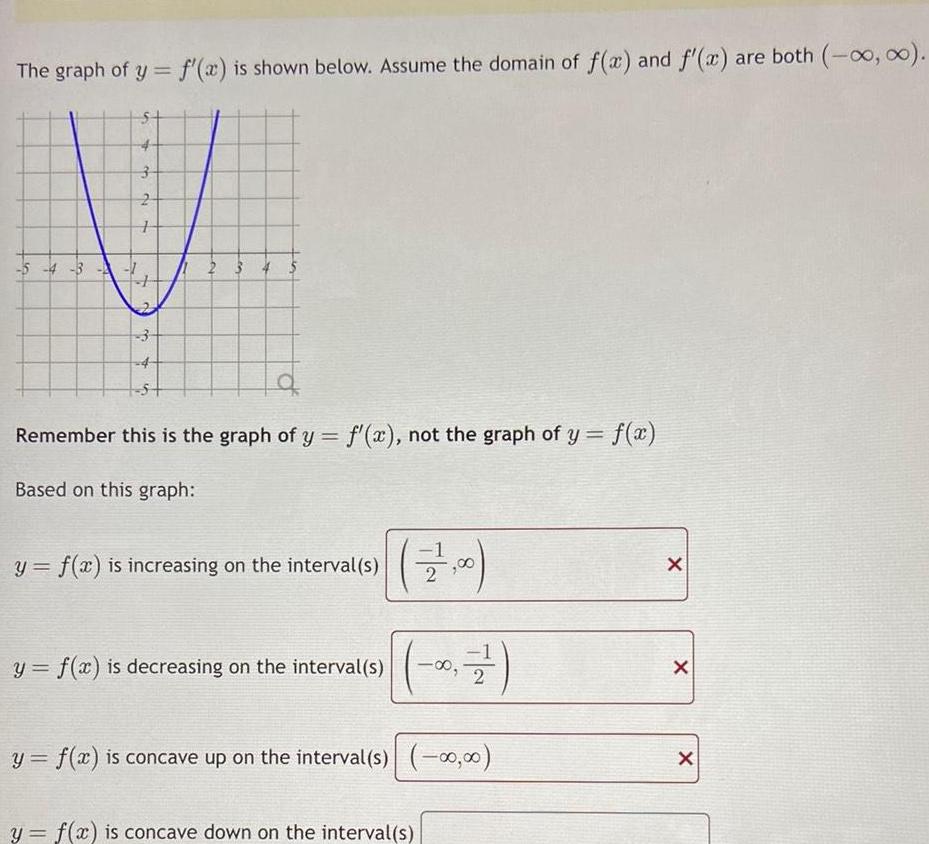
Calculus
Application of derivativesThe graph of y f x is shown below Assume the domain of f x and f x are both 5 4 3 3 2 1 3 23 Remember this is the graph of y f x not the graph of y f x Based on this graph y f x is increasing on the interval s y f x is decreasing on the interval s y f x is concave up on the interval s 00 y f x is concave down on the interval s 2 2 7 00 00 X X X
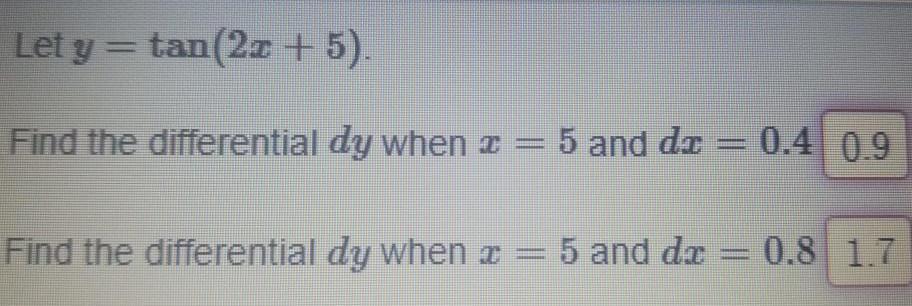
Calculus
Differential equationsLet y tan 2x 5 Find the differential dy when z 5 and di Find the differential dy when 5 and dr 0 4 0 9 0 8 1 7


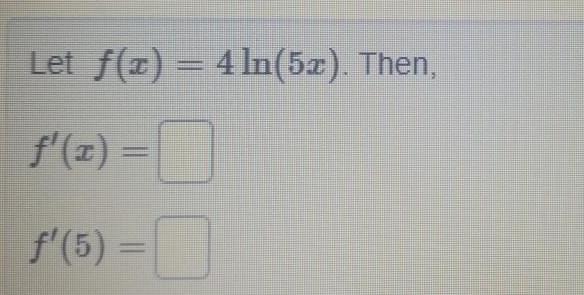
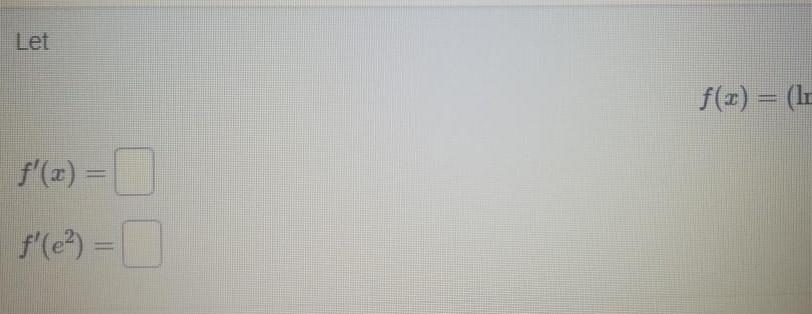

Calculus
Limits & ContinuityFind the solution of the exponential equation in terms of logarithms or correct to four decimal places e 4 16
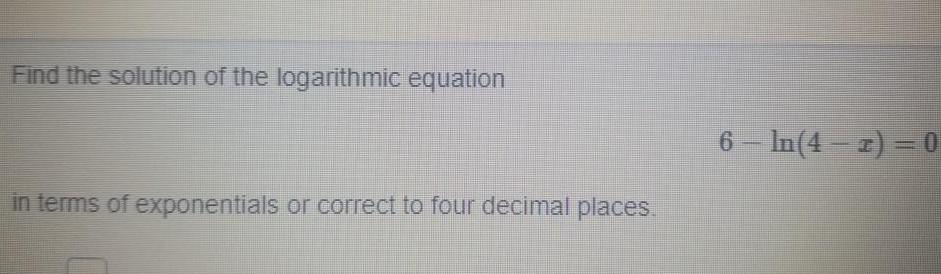
Calculus
Application of derivativesFind the solution of the logarithmic equation in terms of exponentials or correct to four decimal places 6 In 4 2 0
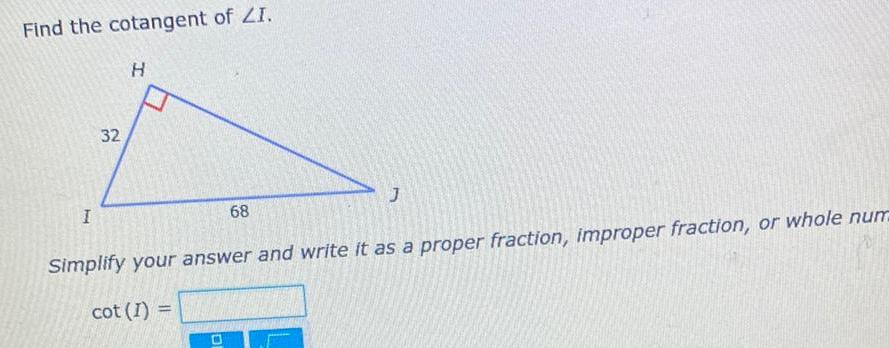
Calculus
Application of derivativesFind the cotangent of ZI I 32 H 68 Simplify your answer and write it as a proper fraction improper fraction or whole num cot 1 0 J

Calculus
Application of derivativesoblem 3 Consider the following equations In each case suppose that we apply the Intermediate Value Theorem using the interval 0 1 i e we take a 0 b 1 in the Intermediate Value Theorem x x 1 0 ii 2e x 4 iii ln x 1 1 2x For which equations does the Intermediate Value Theorem conclude that there must be a root of the equation in the interval 0 1 A i and iii B ii and iii C none of them D iii only E i only F ii only G all of them H i and ii

Calculus
Limits & Continuityy 10 5 TE O O 40 O 5 0 5 Find the rule of the red portion of the function 10 5 10 powered by desmos Find the restricted domain of the red portion of the function Use interval notation

Calculus
Definite IntegralsKaniska Joshi Register No 23 Class XI A 6 Spelling Mistake on the Shaala Darpan Portal Imagine that you are Rabindra Khurana a student of class XI You come to know that there is mistake in the spelling of your name on the portal of Shaala Darpan Write a letter to the principal of your school to update the spelling of your name Ans Ram Mandir Road Matalwas 30 December 20 The Principal Govt Senior Secondary School Matalwas Subject Error in the entry on the Portal of Shaala Darpan Sir Respectfully I am a student of class XI A of your school Yesterday I visited the portal of Shaala Darpan and found out that there was mistake in the spelling of my name It is a kind of clerical error It is as under What is uploaded Ravindra Kurana What must be uploaded Rabindra Khurana I am enclosing my birth certificate and Aadhaar Card for your perusal It will be very kind if you please update it and do the needful With best regards Yours obediently Rabindra Khurana ject For incor spectfully I an at our class has de whole set of the detail of the Hornbill Snapsho fat fet Physics Chemi Biolog We made req tests are at h to us as earl With best re Yours obedi Shantanu S Monitor Class XI A 11 8 Cleanin Imagine th not been cl to clean th

Calculus
DifferentiationEstimate the value of lim 1 0 x 4 21 lim 21 24 Use a table of values to estimate the value of the limit If you have a graphing device use it to confirm your result graphically x 1 23 lim x 1 X 1 10 1 9 t 2 lan 3x x 0 tan 5x 22 lim U 24 lim x 0 3 9 5 X