Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
Calculus
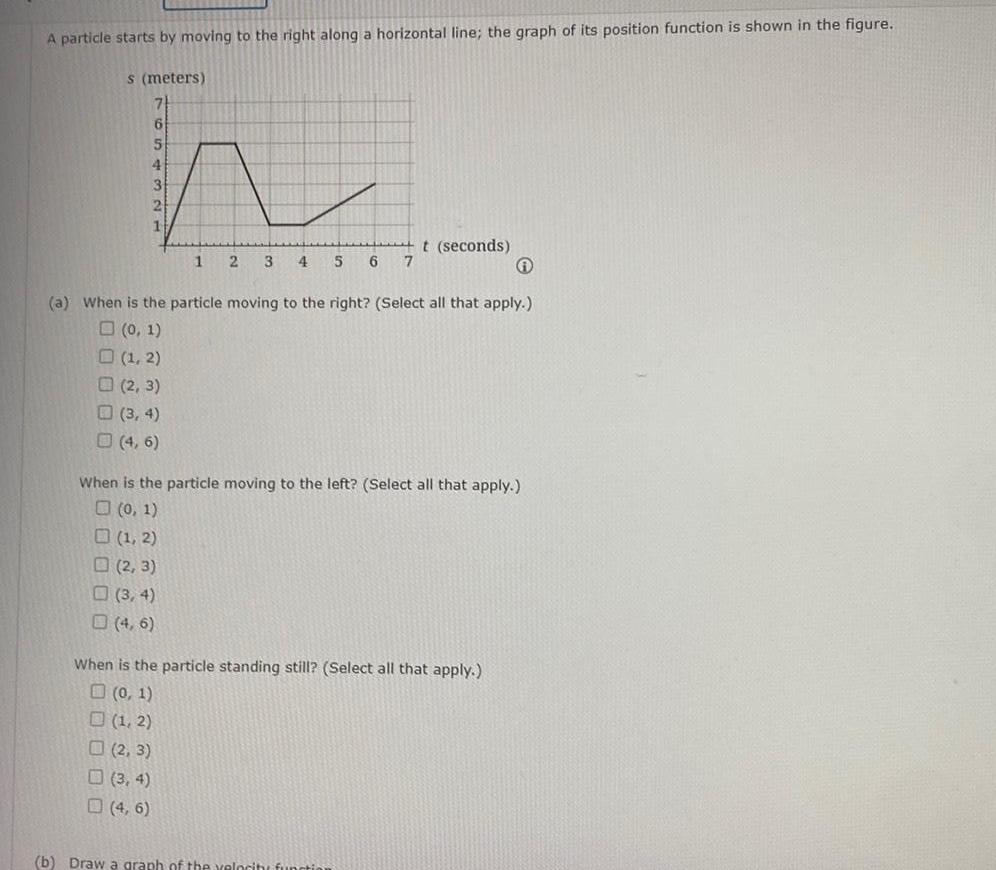
Vector CalculusA particle starts by moving to the right along a horizontal line the graph of its position function is shown in the figure s meters 6 5 4 3 2 1 2 3 3 4 4 6 1 a When is the particle moving to the right Select all that apply 0 1 1 2 1 2 2 3 3 4 4 6 4 6 2 3 4 5 6 7 When is the particle moving to the left Select all that apply 0 1 t seconds When is the particle standing still Select all that apply 0 1 1 2 2 3 b Draw a graph of the velocity functi

Calculus
Differentiation2 The displacement in meters of a particle moving in a straight line is given by the equation of motion s t a t 1 t 2 t 3 V V V V m s m s m s m s where t is measured in seconds Find the velocity in m s of the particle at times t a t 1 t 2 and

Calculus
DifferentiationA ball is thrown into the air with a velocity of 39 ft s Its height in feet after t seconds is given by s t 39t 16t2 Find the velocity in ft s of the ball at time t 1 second ft s
Calculus
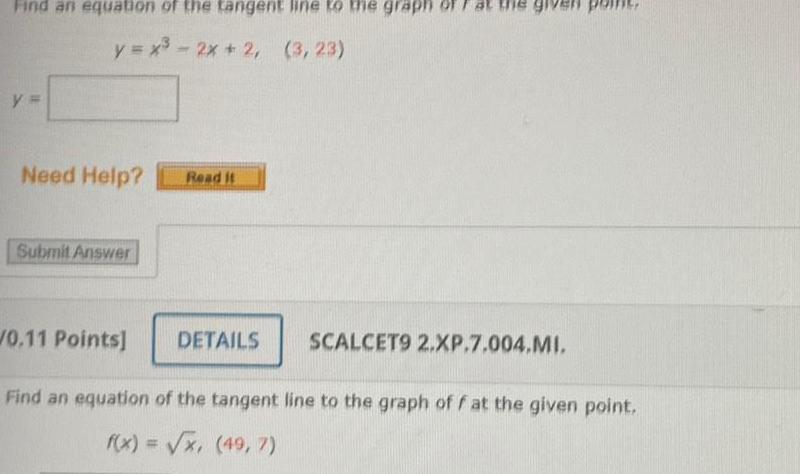
Application of derivativesFind an equation of the tangent line to the graph y x 2x 2 3 23 y Need Help Submit Answer Read it 0 11 Points Find an equation of the tangent line to the graph of f at the given point f x x 49 7 DETAILS SCALCET9 2 XP 7 004 MI

Calculus
Vector CalculusGas mileage actually varies slightly with the driving speed of a car as well as with highway vs city driving Suppose your car averages 27 miles per gallon on the highway if your average speed is 52 miles per hour and it averages 26 miles per gallon on the highway if your average speed is 68 miles per hour Answer parts a and b below C a What is the driving time for a 2900 mile trip if you drive at an average speed of 52 miles per hour What is the driving time at 68 miles per hour The driving time at 52 miles per hour is hours Type an integer or decimal rounded to two decimal places as needed

Calculus
Vector CalculusComplete parts a through c below a A storage pod has a rectangular floor that measures 20 feet by 9 feet and a flat ceiling that is 8 feet above the floor Find the area of the floor and the volume of the pod b A lap pool has a length of 28 yards a width of 20 yards and a depth of 5 yards Find the pool s surface area the water surface and the total volume of water that the pool c A raised flower bed is 30 feet long 4 feet wide and 1 6 feet deep Find the area of the bed and the volume of soil it holds a The area of the floor of the pod is Typo on intogor or o donimel C

Calculus
Application of derivativesIn 2015 there were approximately 4 141 000 births in a country Find the birth rate in births per minute Assuming a population of 336 million what was the annual birth rate in units of births F people The birth rate in units of births per minute is approximately births per minute Round to the nearest tenth as needed

Calculus
Limits & ContinuityComplete parts a through c below a A warehouse is 60 yards long 28 yards wide and 5 yards high What is the area of the warehouse floor If the warehouse is filled to half its height with tightly packed boxes what is the volum of the boxes b A room has a rectangular floor that measures 29 feet by 15 feet and a flat 8 foot ceiling What is the area of the floor and how much air does the room hold c A grain silo has a circular base with an area of 136 square feet and is 23 feet tall What is the total volume a The area of the warehouse floor is

Calculus
Application of derivativesJennifer borrowed 3200 from the bank in order to buy a new dune buggy She will pay it of by equal payments at the end of each week for 4 years The annual interest rate is 6 95 Determine the size of payments and the total interest paid Express your answers rounded to the nearest cent Payments Total interest
Calculus
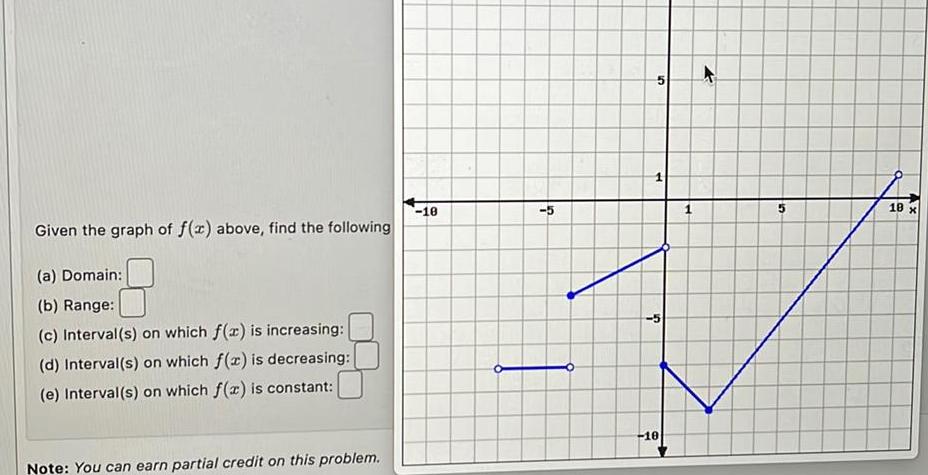
Limits & ContinuityGiven the graph of f x above find the following a Domain b Range c Interval s on which f x is increasing d Interval s on which f x is decreasing e Interval s on which f x is constant Note You can earn partial credit on this problem 18 5 10 18 x
Calculus
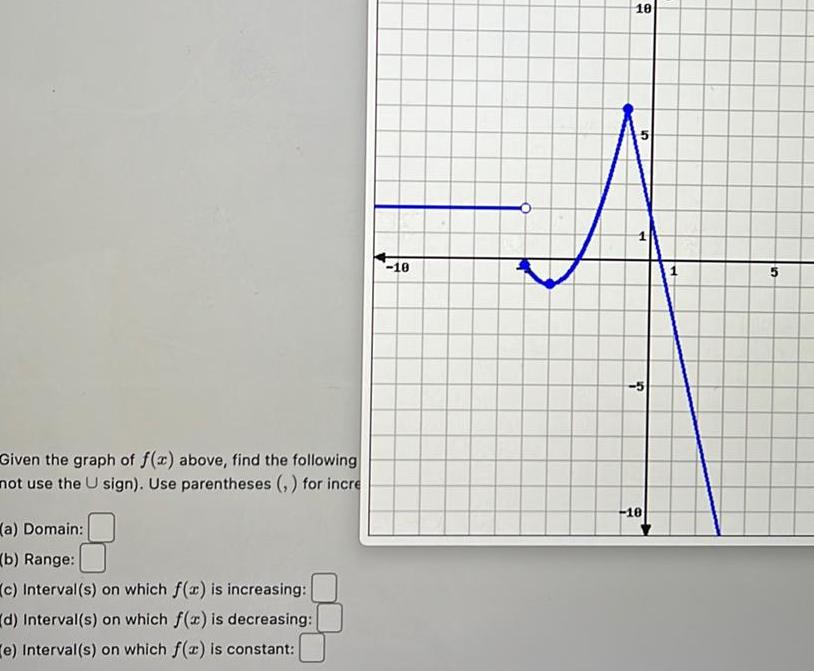
Limits & ContinuityGiven the graph of f x above find the following not use the U sign Use parentheses for incre a Domain b Range c Interval s on which f x is increasing d Interval s on which f x is decreasing e Interval s on which f x is constant 10 10 c 10 5
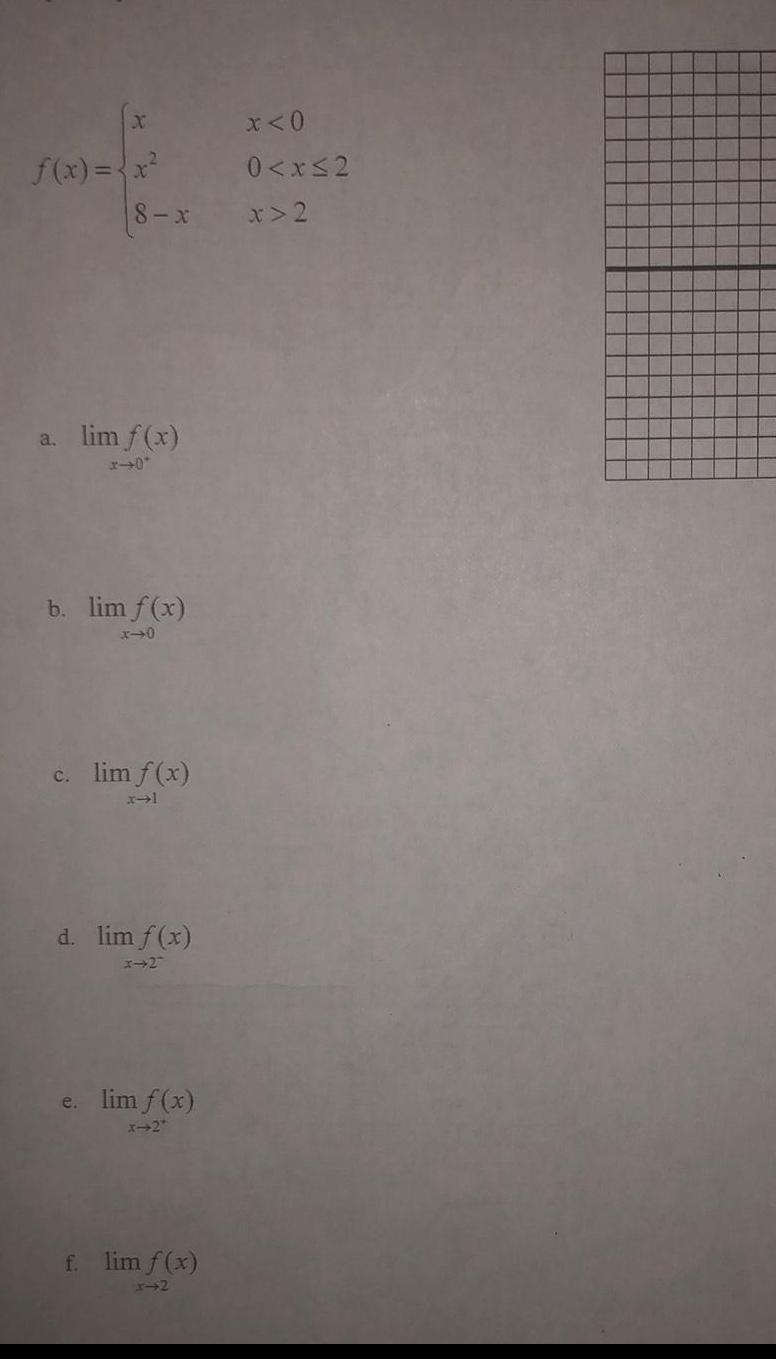
Calculus
Application of derivativesX f x x 8 x a lim f x x 0 b lim f x x 0 c lim f x x 1 d lim f x x 2 e lim f x X 2 f lim f x x 2 x 0 0 x 2 x 2

Calculus
Vector Calculusa f x Subsequently we used that fact to compare the value of the integral with the value of an antiderivative obtained by using integration rules Now suppose on one hand f x is integrable but cannot be differentiated using the integration rules available On the other hand the integral can be evaluated numerically for any value of x Many functions belong in this category For the moment however we focus on one particular function f x This function was the only power function not handled by the integration power rule consequently we could not obtain an expression for the antiderivative As we see in Section 7 1 an antiderivative can be found using our general expression in the first paragraph and it is the natural logarithmic function Procedure Go to desmos com 1 Plot the function f x over the interval 1 10 Go to the wrench at the top right of your screen and change the x axis to be 0 11 with 1 0 step and y scale to be 0 2 with 0 5 step Uncheck the box for minor gridlines 2 Without using calculus just by looking at the graph try to find a rough estimate of the area between the graph of f x and the x axis from x 1 to x 2 Hint what is the area of each rectangle Repeat this for x going from 1 to 5 Although tedious and inaccurate the process you just followed could be repeated to get an estimate of the area from x 1 to x a for any a 1 For any value of a we input the output is a number i e a function F a the area between f x and the x axis from x 1 to x a 3 In Desmos define F a to be the integral from 1 to a of 1 x dx To get an integral in desmos type int and the integral sign will appear a Evaluate F 2 b Evaluate F 5 c Do your estimates match your answers from question 2 4 Turn off the plot of f x Turn on the plot for F a if not already done Now graph In x on the interval from 0 1 to 10 In x 0 1 x 10 Zoom in or out as needed to see both graphs What do you notice 5 Evaluate In 0 5 and In 1 0 Interpret each of these answers in terms of the integral and area between the curve and the x axis Note we do not define In a for a 0 or for negative values of a 6 Evaluate the following In 2 In 5 In 5 In 2 5ln 2 In 2 5 In 5 2 In 2 5 7 State the logarithmic properties responsible for making the expressions equal 8 Interpret your answers from one side of the table either side in terms of the integral and area between the curve and the x axis The goal here is to see why in terms of the integral or area under the curve the right side equals the left side of the table We are looking for your thoughts here not a specific right answer 1 9 Type the integral dxinto Desmos Anything surprising How do you explain this 2 answer other than the fact we know F a is only defined for a 0 a Determine the exact value of this integral by hand 10 From Calculus A we learned that if a continuous function f on a closed interval a b takes values f a and f b at each end of the interval then it also takes any value between f a and f b at some point within the interval Since In 2 1 and In 5 1 by IVT there exists a value between x 2 and x 5 where In x 1 We obtain an approximation to
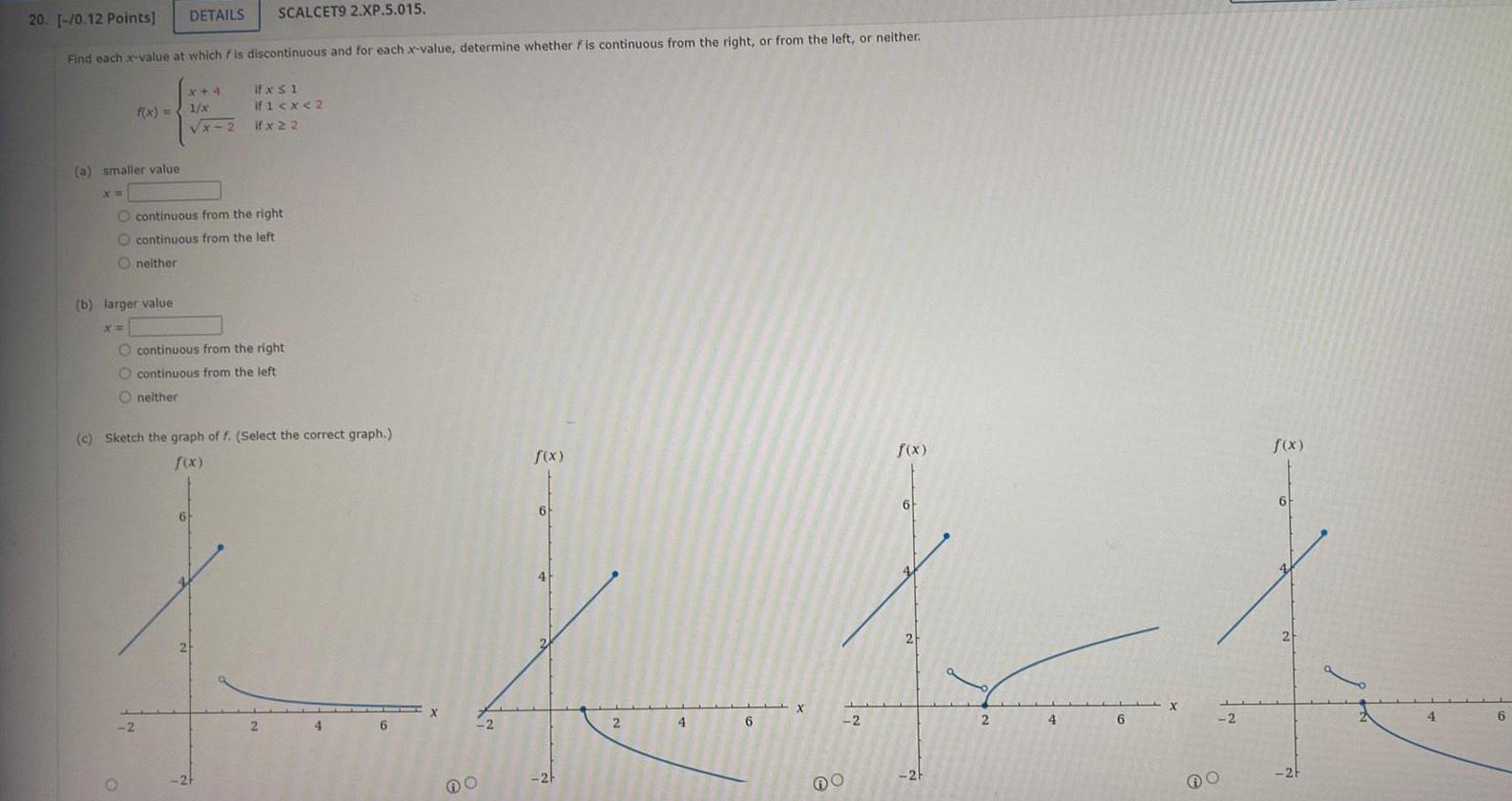
Calculus
Limits & Continuity20 0 12 Points DETAILS SCALCET9 2 XP 5 015 Find each x value at which is discontinuous and for each x value determine whether fis continuous from the right or from the left or neither a smaller value X f x Oneither b larger value X O continuous from the right O continuous from the left x 4 lfxs1 1 x x 2 2 if 1 x 2 lfx22 O continuous from the right O continuous from the left Oneither 6 c Sketch the graph of f Select the correct graph f x 2 4 6 2 f x 6 2 4 6 X 2 f x 6 2 2 4 6 2 f x 6 2 4 6
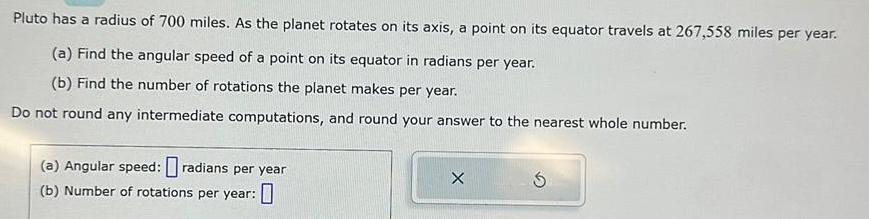
Calculus
DifferentiationPluto has a radius of 700 miles As the planet rotates on its axis a point on its equator travels at 267 558 miles per year a Find the angular speed of a point on its equator in radians per year b Find the number of rotations the planet makes per year Do not round any intermediate computations and round your answer to the nearest whole number a Angular speed radians per year b Number of rotations per year X
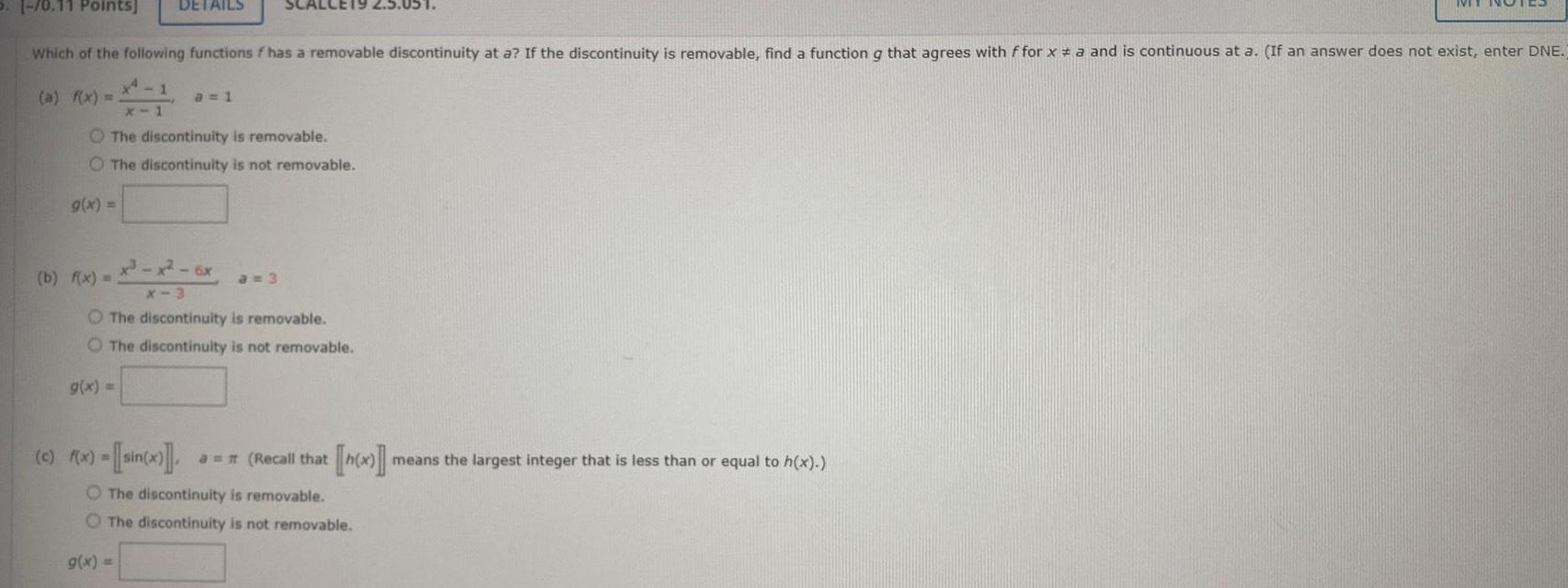
Calculus
Application of derivativesS 0 11 Points DETAILS Which of the following functions f has a removable discontinuity at a If the discontinuity is removable find a function g that agrees with ffor x a and is continuous at a If an answer does not exist enter DNE a f x The discontinuity is removable O The discontinuity is not removable g x a 1 x x 6x X 3 O The discontinuity is removable The discontinuity is not removable b f x g x a 3 c f x sin x a Recall that h x means the largest integer that is less than or equal to h x O The discontinuity is removable O The discontinuity is not removable g x
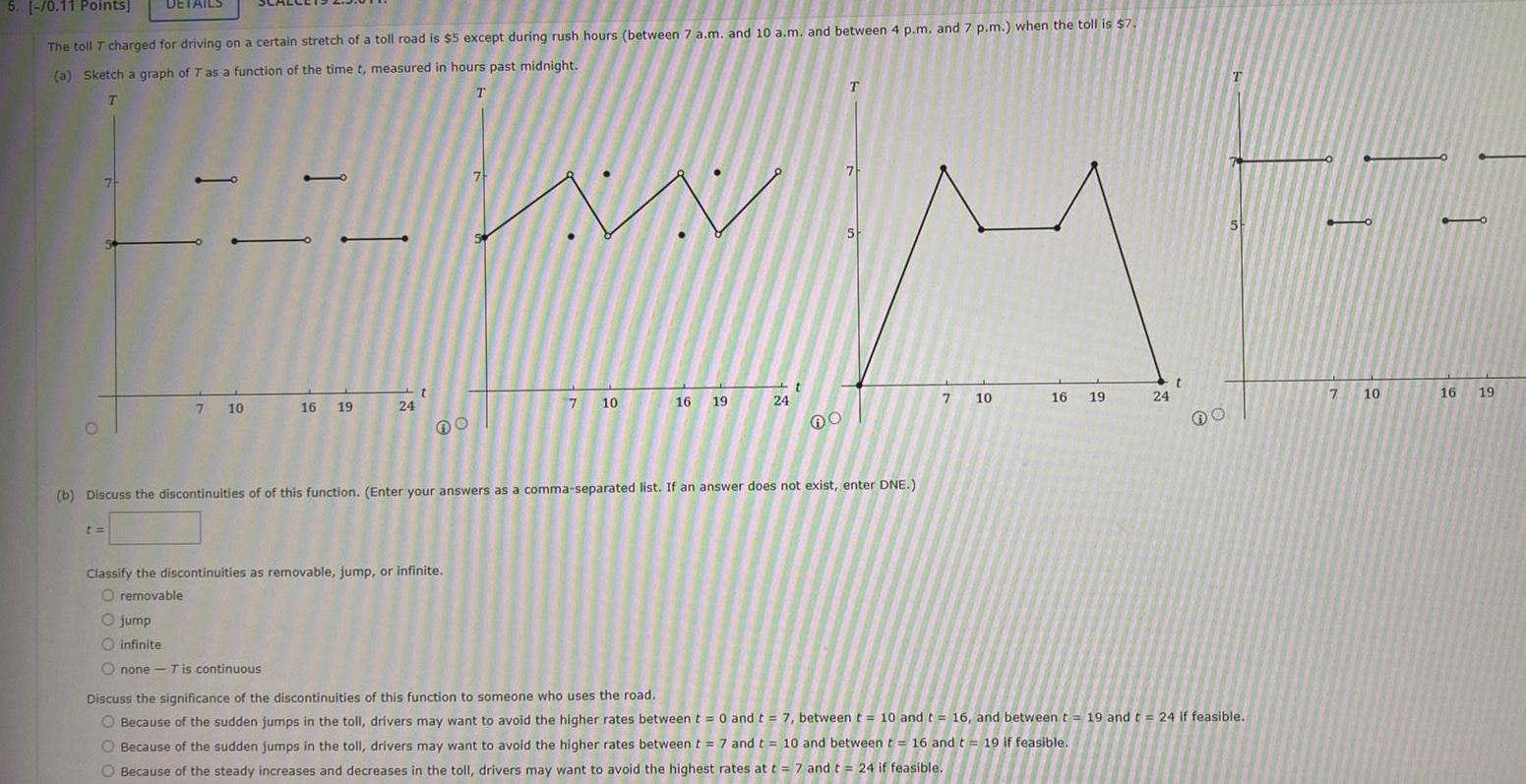
Calculus
Limits & Continuity5 0 11 Points The toll T charged for driving on a certain stretch of a toll road is 5 except during rush hours between 7 a m and 10 a m and between 4 p m and 7 p m when the toll is 7 a Sketch a graph of T as a function of the time t measured in hours past midnight T T O DETAILS t FFW 7 10 16 19 jump infinite Onone T is continuous 24 t DO Classify the discontinuities as removable jump or infinite O removable 7 7 10 16 19 24 T b Discuss the discontinuities of of this function Enter your answers as a comma separated list If an answer does not exist enter DNE 7 5 7 10 16 19 24 t O T Discuss the significance of the discontinuities of this function to someone who uses the road O Because of the sudden jumps in the toll drivers may want to avoid the higher rates between t 0 and t 7 between t 10 and t 16 and between t 19 and t 24 if feasible Because of the sudden jumps in the toll drivers may want to avoid the higher rates between t 7 and t 10 and between t 16 and t 19 if feasible O Because of the steady increases and decreases in the toll drivers may want to avoid the highest rates at t 7 and t 24 if feasible 7 10 90 16 19
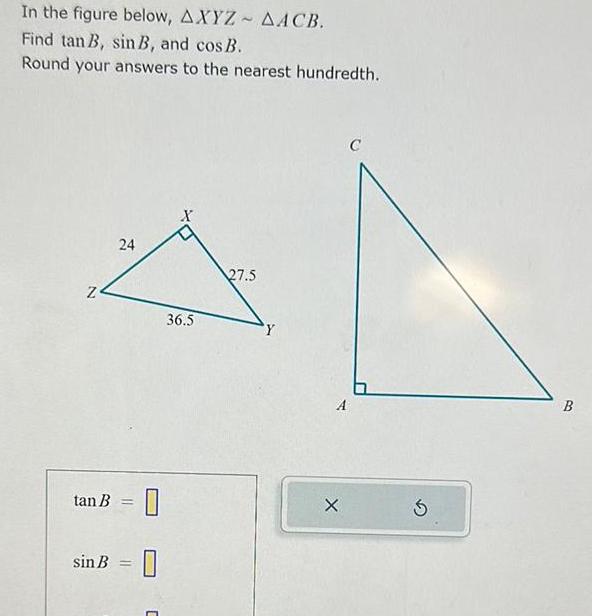
Calculus
Application of derivativesIn the figure below AXYZ AACB Find tan B sin B and cos B Round your answers to the nearest hundredth N 24 tan B sinB 36 5 27 5 Y A X B

Calculus
Limits & Continuityx x 7 0 1 2 f x x x 7 is Select on the closed interval 1 2 f 1 in the specified interval and f 2 Since 5 11 there is a number c in 1 2 such that f c by the Intermediate Yalue Theorem

Calculus
DifferentiationUsing scientific notation convert the following 1 nL mL Write your answer in the form of 1x10 to show an exponent due to formatting in C

Calculus
DifferentiationWhich of the following are continuous functions Select all that apply O The temperature at a specific location as a function of time The temperature at a specific time as a function of the distance due west from New York City The altitude above sea level as a function of the distance due west from New York City The cost of a taxi ride as a function of the distance traveled The current in the circuit for the lights in a room as a function of time None of these

Calculus
Limits & ContinuityIf f is continuous on co co what can you say about its graph Select all that apply The graph of f has a hole The graph of f has a jump The graph of f has a vertical asymptote Onone of these
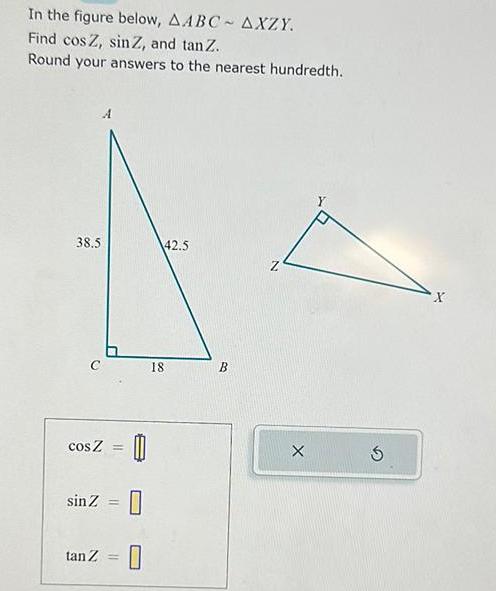
Calculus
DifferentiationIn the figure below AABC AXZY Find cos Z sin Z and tan Z Round your answers to the nearest hundredth 38 5 cos z sinZ 0 0 tan Z 18 42 5 BO X S X
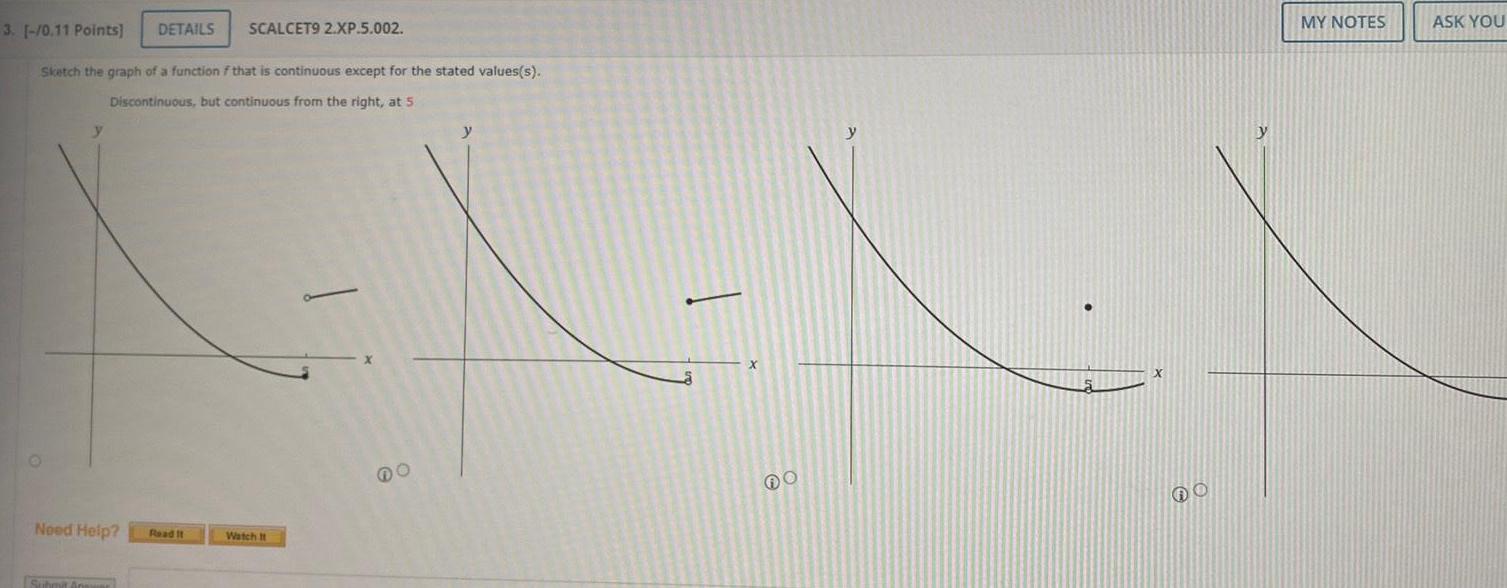
Calculus
Limits & Continuity3 0 11 Points Sketch the graph of a function f that is continuous except for the stated values s Discontinuous but continuous from the right at 5 Need Help DETAILS SCALCET9 2 XP 5 002 Submit An Read It Watch It y DO O MY NOTES ASK YOU
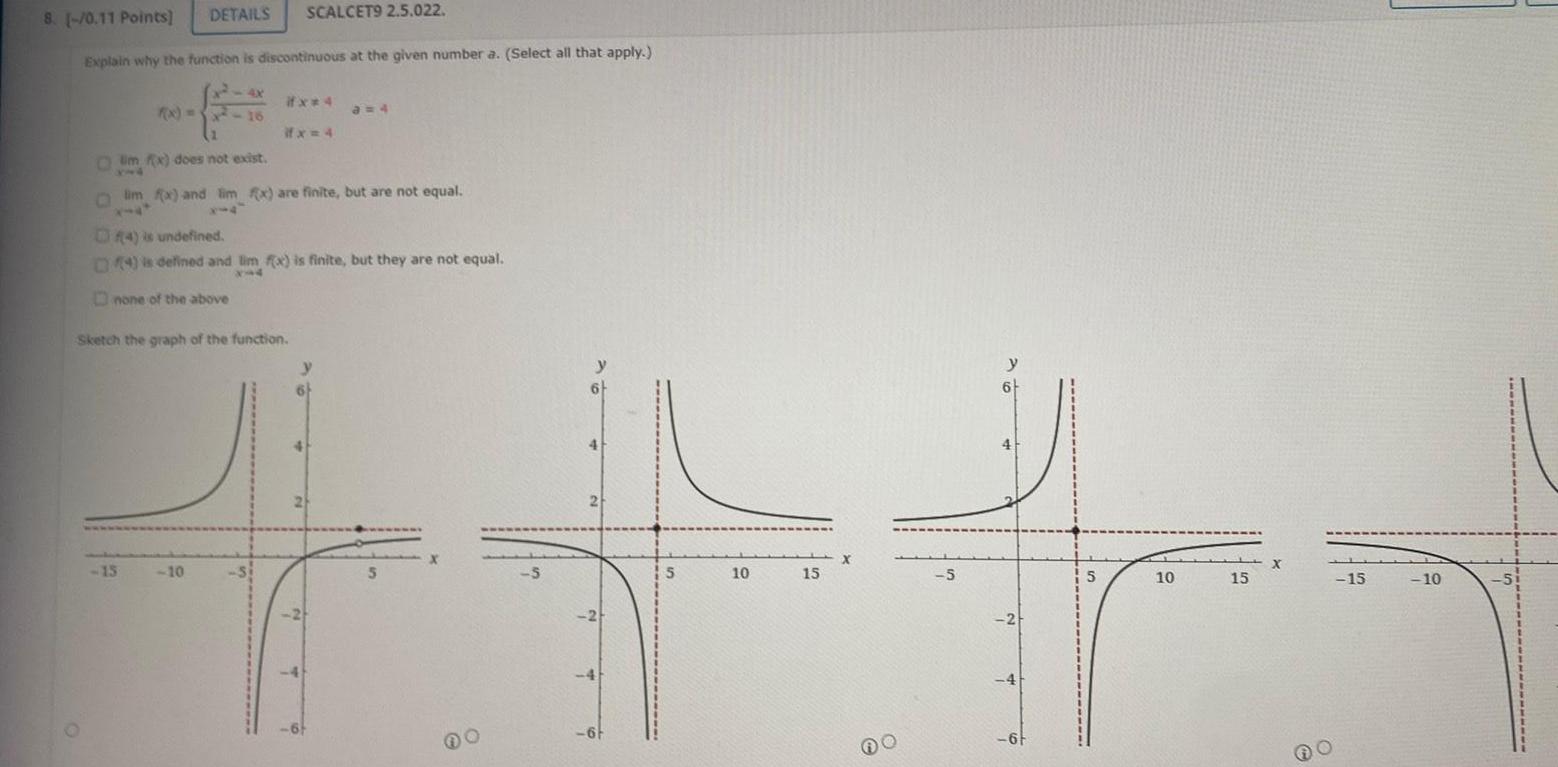
Calculus
Application of derivativesDETAILS 8 0 11 Points Explain why the function is discontinuous at the given number a Select all that apply 4X 15 SCALCET9 2 5 022 10 x 4 Om fx does not exist lim f x and lim x are finite but are not equal Sketch the graph of the function 4 is undefined 4 is defined and lim f x is finite but they are not equal none of the above a 4 4 5 5 y 6 4 2 2 6F 5 10 15 5 y 6 4 2 4 6F 5 10 15 X 15 10 5 1 1 1
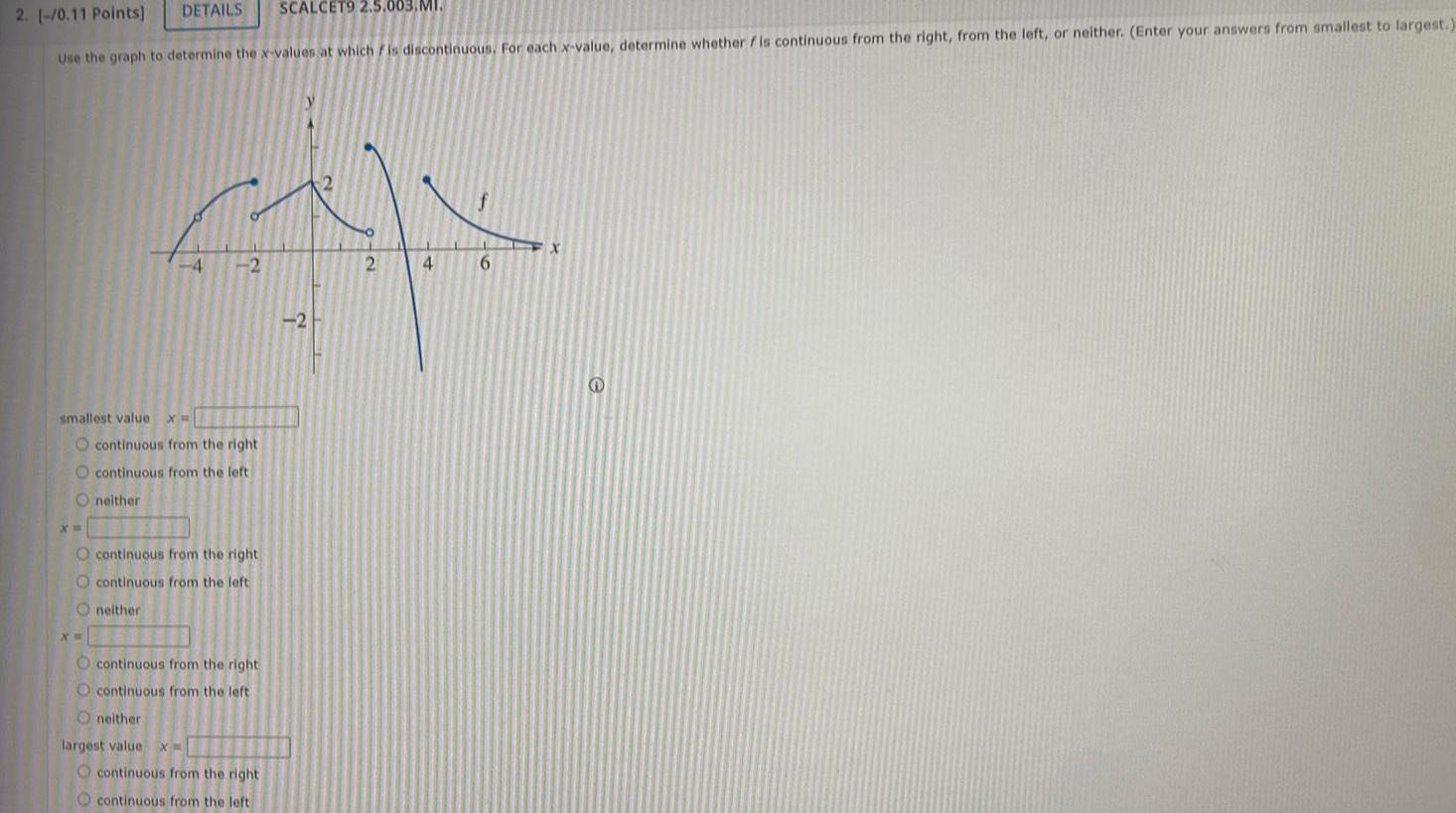
Calculus
Limits & Continuity2 0 11 Points DETAILS SCALCET9 2 5 003 MI Use the graph to determine the x values at which is discontinuous For each x value determine whether fis continuous from the right from the left or neither Enter your answers from smallest to largest smallest value x O continuous from the right continuous from the left Oneither X 4711 2 2 O continuous from the right O continuous from the left Oneither O continuous from the right O continuous from the left O neither largest value X O continuous from the right continuous from the left 2 6 X
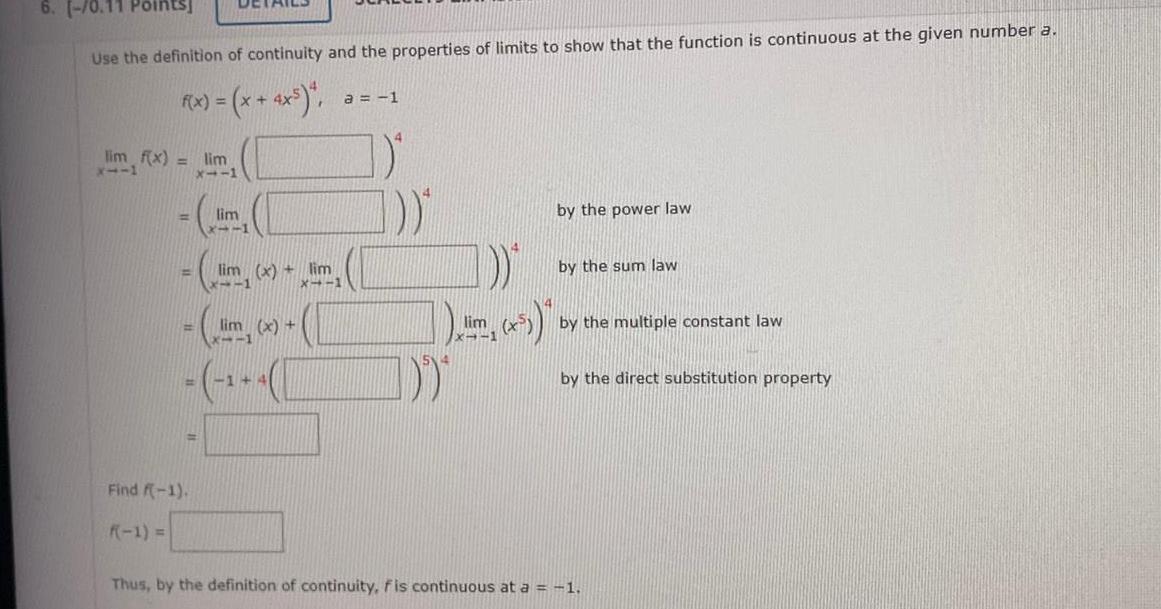
Calculus
Limits & Continuity6 Use the definition of continuity and the properties of limits to show that the function is continuous at the given number a f x x 4x lim f x X111 lim X 11 Find f 1 F 1 lim lin lim x 1 lim x lim x 1 x 1 144 a 1 D D x lim x by the power law by the sum law by the multiple constant law by the direct substitution property Thus by the definition of continuity fis continuous at a 1
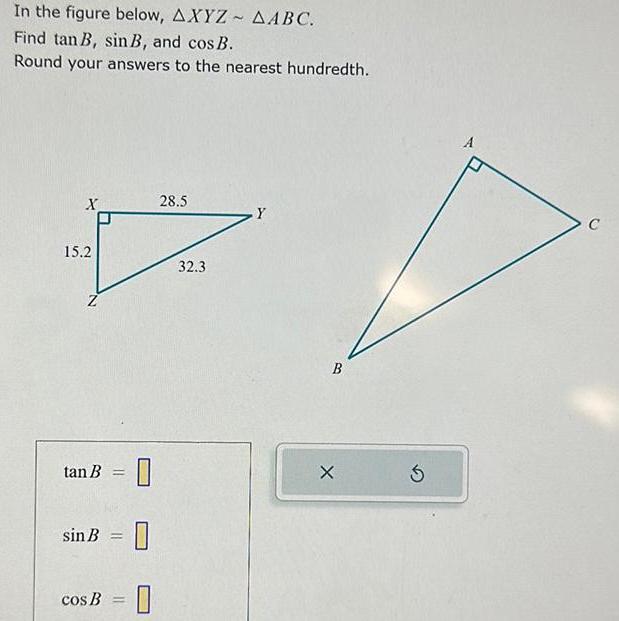
Calculus
DifferentiationIn the figure below AXYZ AABC Find tan B sin B and cos B Round your answers to the nearest hundredth X 15 2 tan B sin B cos B 0 0 0 28 5 32 3 Y B X

Calculus
DifferentiationFind the values of a and b that make f continuous everywhere a b f x x 4 X 2 ax bx 3 2x a b if x 2 if 2 x 3 if x 3

Calculus
Definite Integrals7 10 points Consider the contour map below of the popular hiking area known with the famous potato chip rock Suppose that f x y is the function that gives the vertical height in feet of the mountain over a point x y 008 a 2 points Assume the lines are level curves that are equally spaced What is the elevation at the point P Answer b 3 points Draw a vector at Q in the direction of Vf Q 000 i f c 0 1600 ii At t 1 f c t 0 iii At t 2 f c t 0 iv At t 3 f c t 0 v ALSO at t 3 f c t P c 5 points Draw ONE curve c t for 0 t 4 on the graph with ALL of the following properties Label time stamps for t 0 t 1 t 2 t 3 for your curve

Calculus
Differential equations7 Let f x a Calculate f x for each value of x in the following table x 4 X b Make a conjecture about the value of lim X 11 2 4 X 2 1 9 12x 2 1 99 1 999 1 9999 2 1 2 01 2 001 2 0001

Calculus
Limits & Continuity9 Let g 1 t 9 Vt 3 a Make two tables one showing values of g for t 8 9 8 99 and 8 999 and one showing values of g for t 9 1 9 01 and 9 001 t 9 9 Vt 3 b Make a conjecture about the value of lim
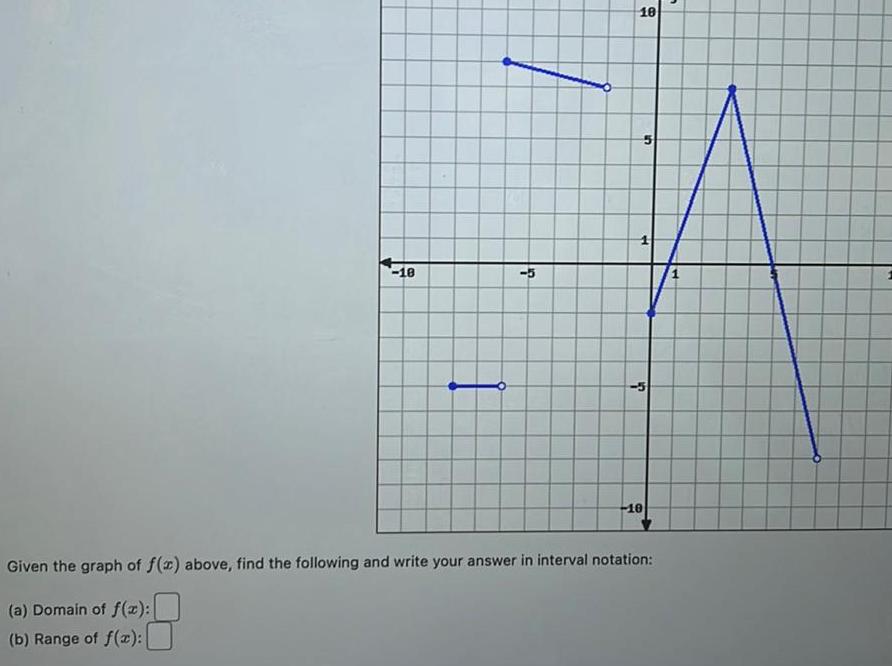
Calculus
Differentiation18 5 10 5 ch 10 Given the graph of f x above find the following and write your answer in interval notation a Domain of f x b Range of f x

Calculus
Vector Calculus75 82 Evaluating inverse trigonometric functions Without using a calculator evaluate the following expressions 75 tan V3 77 sec 2 79 tan tan 7 4 1 81 csc sec 2 76 cot 1 3 78 csc 1 80 tan tan 3 4 82 tan tan 1
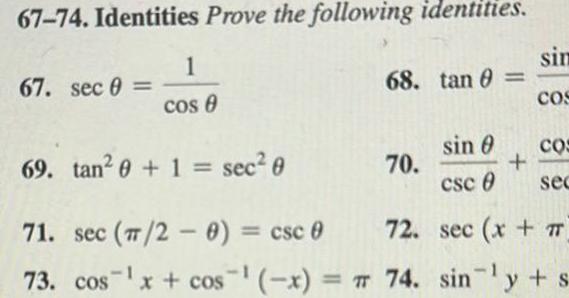
Calculus
Limits & Continuity67 74 Identities Prove the following identities 67 sec 0 1 cos 0 69 tan 0 1 sec 0 71 sec 20 csc 0 73 cos x cos x 68 tan 0 sin 0 csc 0 72 sec x 7 74 siny s 70 sim COS COS sec


Calculus
Limits & ContinuityLocation of vertical asymptotes Let f x the following limits and find the vertical asymptotes of f Verify your work with a graph ing utility a lim f x 21 b lim f x 2 1 c lim f x 1 1 Untitled Graph 1 4x 3 2 1 X 10 Evaluate desmos
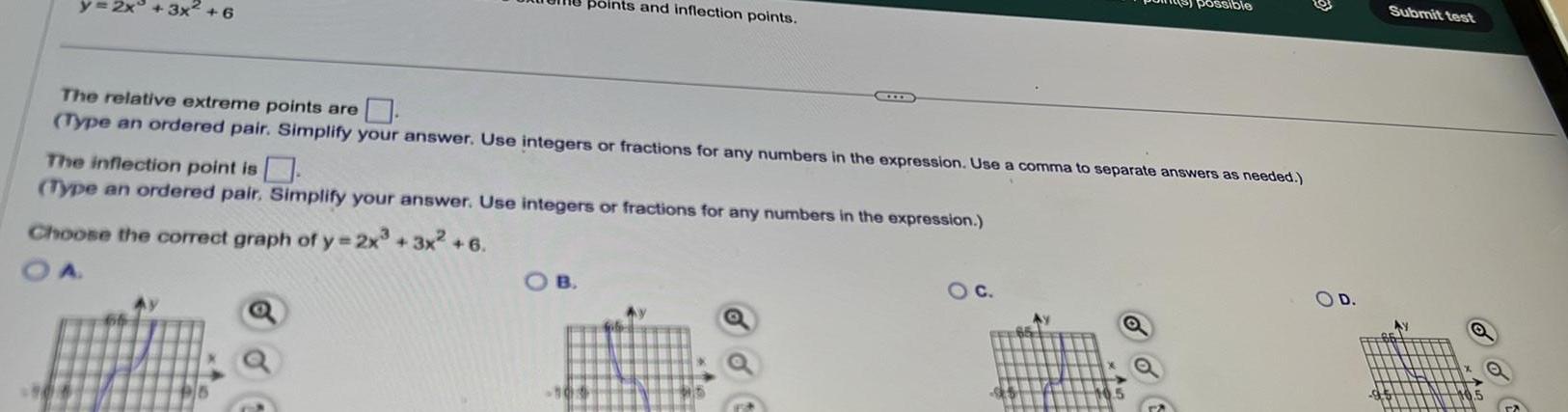
Calculus
Differentiation3x 6 points and inflection points The relative extreme points are Type an ordered pair Simplify your answer Use integers or fractions for any numbers in the expression Use a comma to separate answers as needed The inflection point is Type an ordered pair Simplify your answer Use integers or fractions for any numbers in the expression Choose the correct graph of y 2x 3x 6 OB possible O C O D Submit test

Calculus
Definite Integrals1 10 points Find the volume of the solid region under the surface z x y e and over the rectangle 0 1 x 1 3 in the x y plane
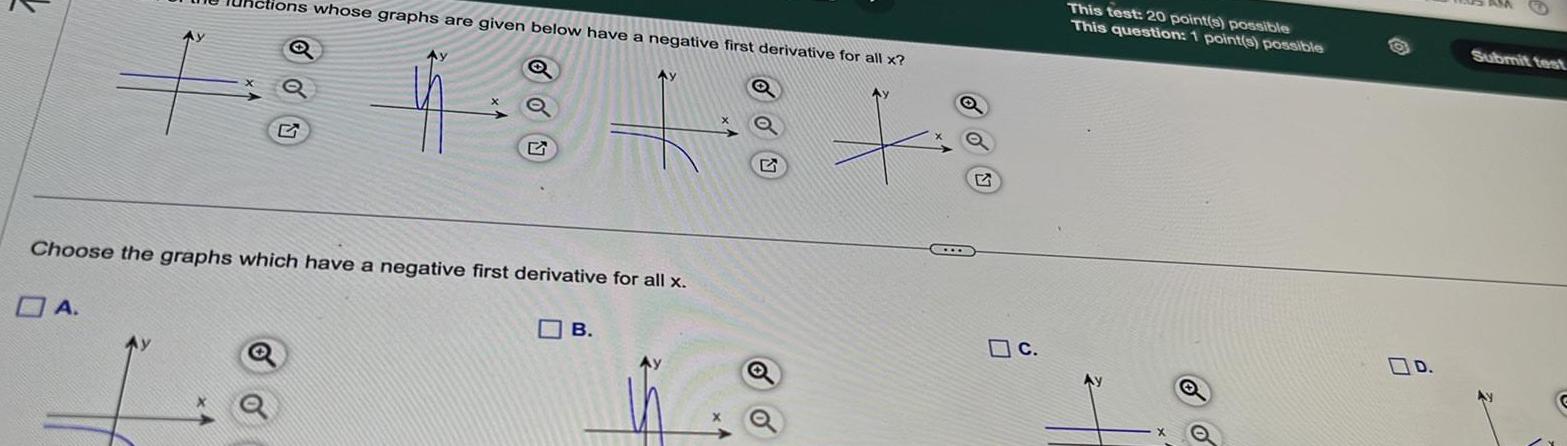
Calculus
Definite Integralstions whose graphs are given below have a negative first derivative for all x Q 4 Choose the graphs which have a negative first derivative for all x A B Q c This test 20 point s possible This question 1 point s possible o D Submit test
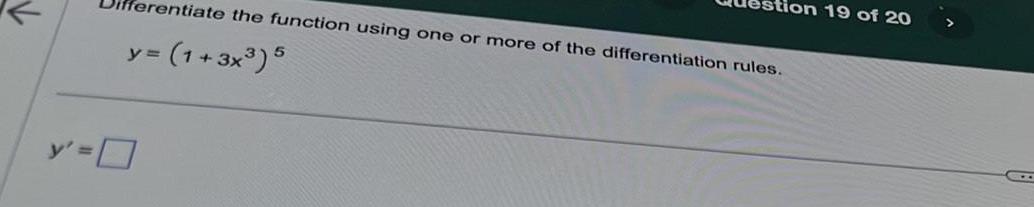
Calculus
Differentiationerentiate the function using one or more of the differentiation rules 1 3x 5 y ion 19 of 20
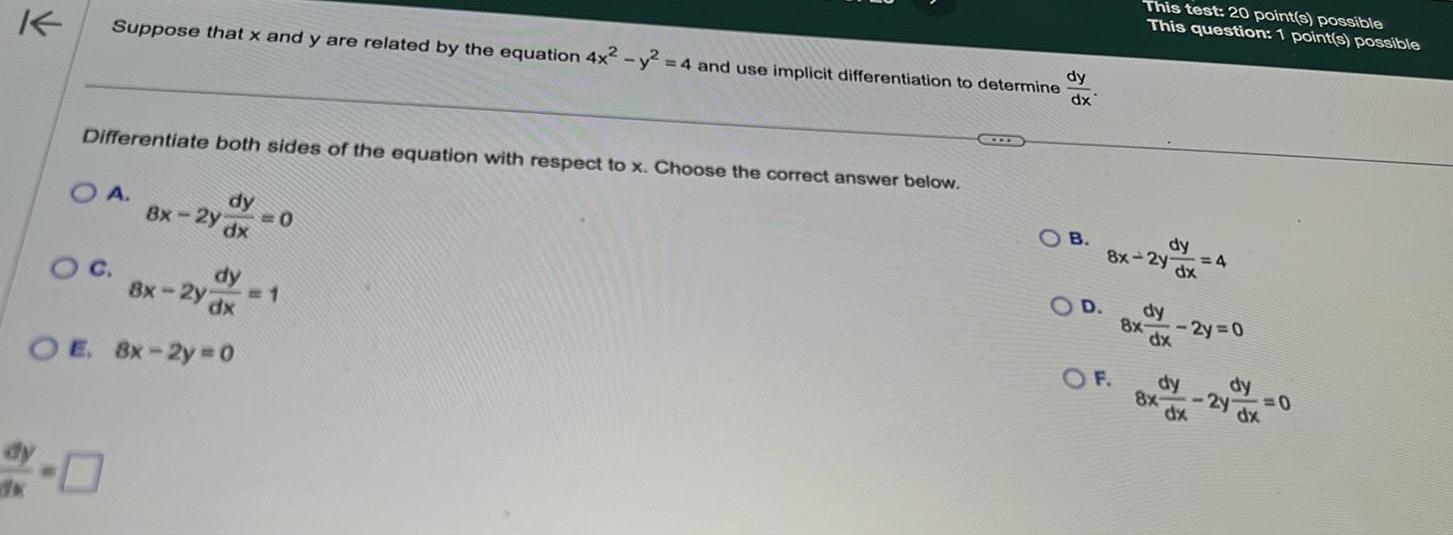
Calculus
Application of derivativesK Suppose that x and y are related by the equation 4x y Differentiate both sides of the equation with respect to x Choose the correct answer below O A dy 8x 2y dx O C dy Bx 2y dx OE 8x 2y 0 0 4 and use implicit differentiation to determine 1 X dy dx OB This test 20 point s possible This question 1 point s possible dy 8x 2y dx COD dy 4 8x 2y 0 dx O F dy dy dx 8x 2y 0
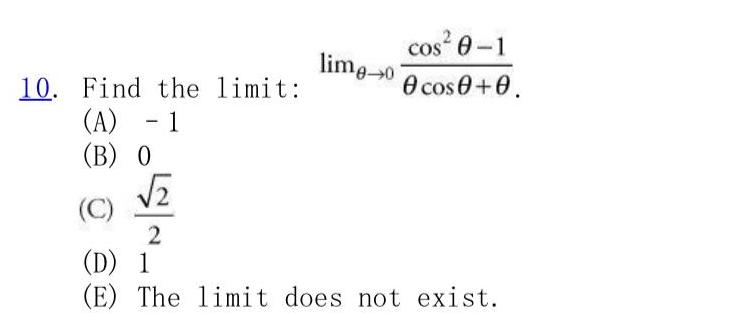
Calculus
Vector Calculus10 Find the limit A 1 B O lime o 2 cos 0 1 0 cos 0 0 C D 1 E The limit does not exist
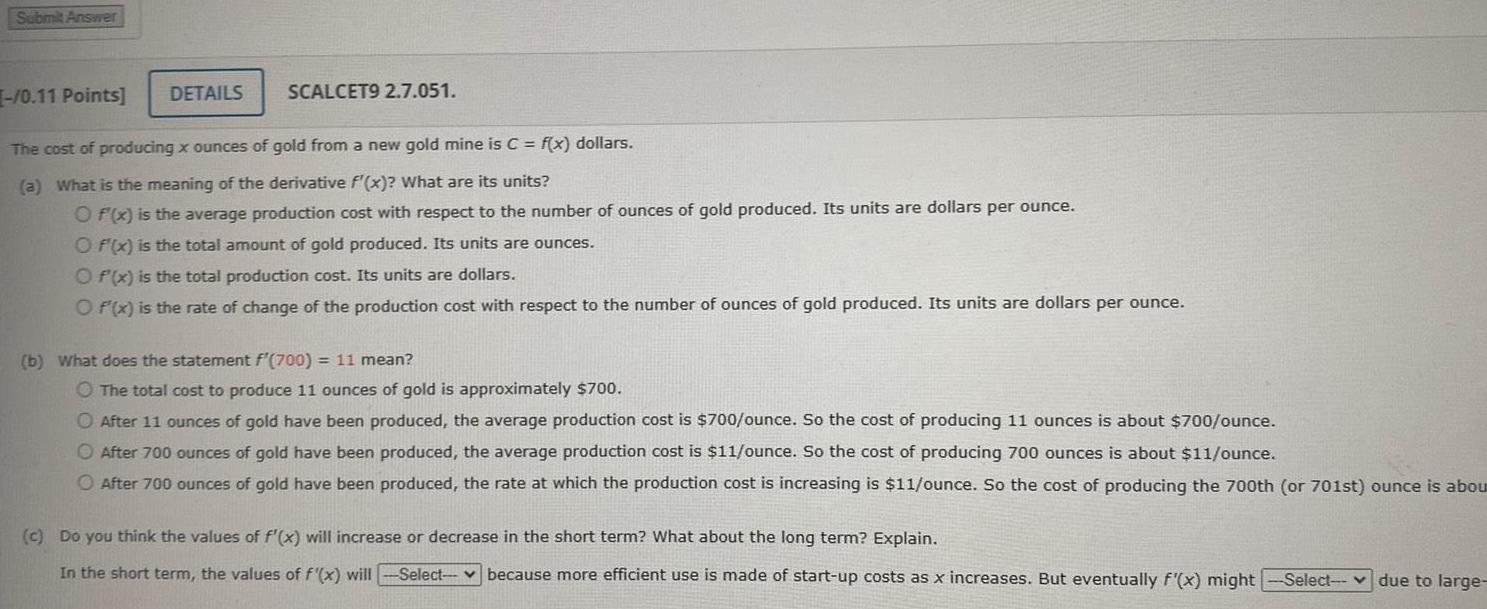
Calculus
Vector CalculusSubmit Answer 0 11 Points DETAILS SCALCET9 2 7 051 The cost of producing x ounces of gold from a new gold mine is C f x dollars a What is the meaning of the derivative f x What are its units O f x is the average production cost with respect to the number of ounces of gold produced Its units are dollars per ounce O f x is the total amount of gold produced Its units are ounces Of x is the total production cost Its units are dollars O f x is the rate of change of the production cost with respect to the number of ounces of gold produced Its units are dollars per ounce b What does the statement f 700 11 mean O The total cost to produce 11 ounces of gold is approximately 700 O After 11 ounces of gold have been produced the average production cost is 700 ounce So the cost of producing 11 ounces is about 700 ounce O After 700 ounces of gold have been produced the average production cost is 11 ounce So the cost of producing 700 ounces is about 11 ounce O After 700 ounces of gold have been produced the rate at which the production cost is increasing is 11 ounce So the cost of producing the 700th or 701st ounce is abou c Do you think the values of f x will increase or decrease in the short term What about the long term Explain In the short term the values of f x will Select because more efficient use is made of start up costs as x increases But eventually f x might Select due to large
Calculus
Vector CalculusA machinist is required to manufacture a circular metal disk with area 1200 cm a What radius produces such a disk Round your answer to four decimal places b If the machinist is allowed an error tolerance of 18 cm in the area of the disk how close to the ideal radius in part a must the machinist control the radius Round your answers to four decimal places cm r cm c In terms of the s definition of lim f x L what is x x a cm Oarea Otarget radius radius target area Otolerance in the area What is f x Oarea O target radius radius O target area O tolerance in the area What is a area target radius radius O target area Otolerance in the area What is L area target radius radius
Calculus
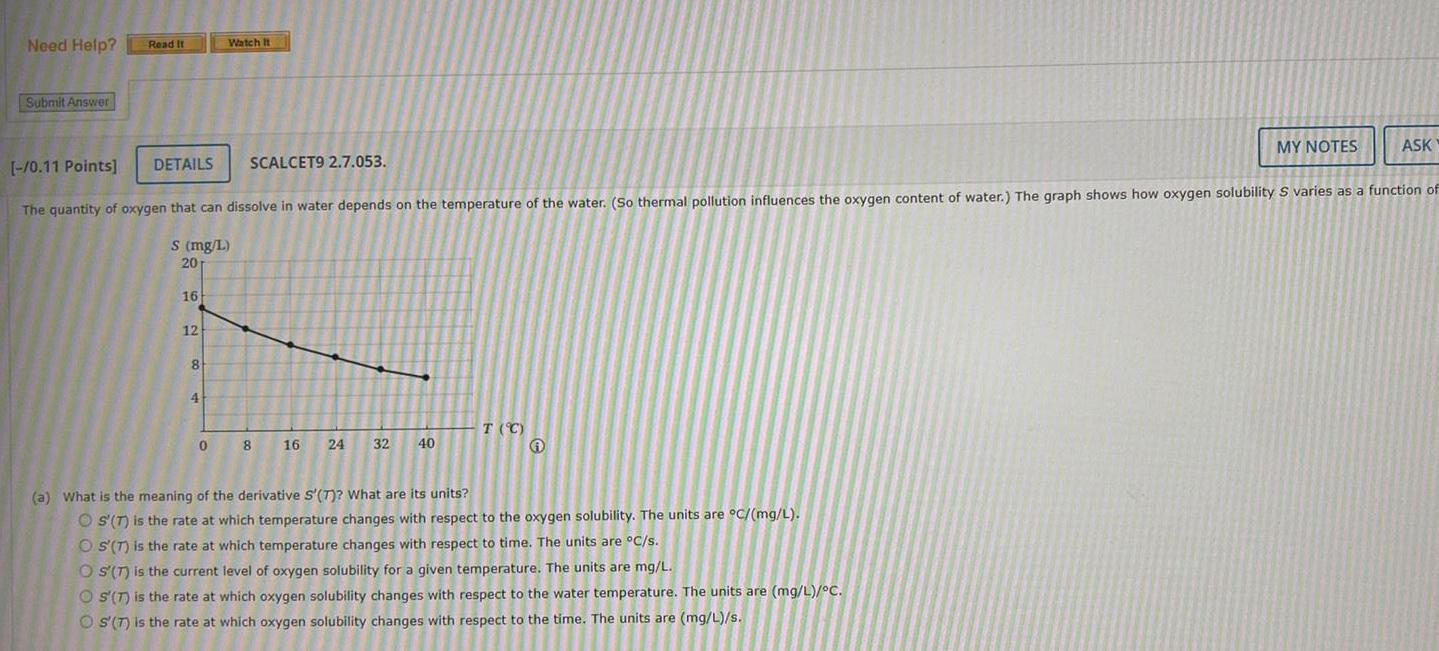
DifferentiationNeed Help Submit Answer Read It DETAILS 16 12 8 0 11 Points The quantity of oxygen that can dissolve in water depends on the temperature of the water So thermal pollution influences the oxygen content of water The graph shows how oxygen solubility S varies as a function of s mg L 20 4 Watch It 0 SCALCET9 2 7 053 8 16 24 32 40 T C MY NOTES a What is the meaning of the derivative S T What are its units OS T is the rate at which temperature changes with respect to the oxygen solubility The units are C mg L OS T is the rate at which temperature changes with respect to time The units are C s OS T is the current level of oxygen solubility for a given temperature The units are mg L OS T is the rate at which oxygen solubility changes with respect to the water temperature The units are mg L C OS T is the rate at which oxygen solubility changes with respect to the time The units are mg L s ASK
Calculus
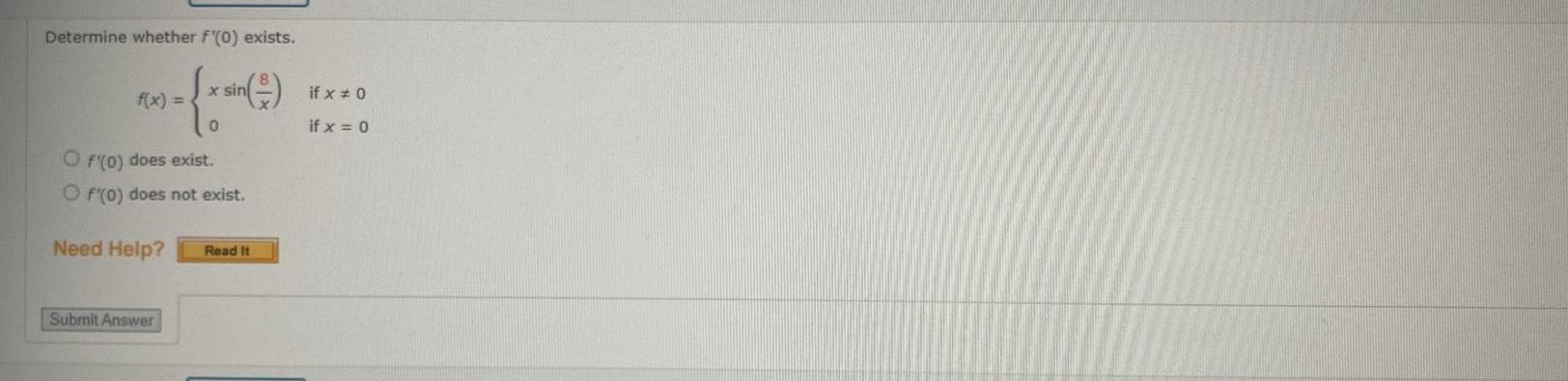
DifferentiationDetermine whether f 0 exists x sin 0 O f 0 does exist O f 0 does not exist Need Help Submit Answer Read It if x 0 if x 0
Calculus
Application of derivativest 2 t 3 V V Need Help Submit Answer 1 x 103 S Read It ii x 101 m s m s 7 0 11 Points The cost in dollars of producing x units of a certain commodity is C x 7 000 10x 0 05x a Find the average rate of change in per unit of C with respect to x when the production level is changed from x 100 to the given value Round your answers to the nearest c DETAILS Watch It Master it SCALCET9 2 7 049 per unit per unit b Find the instantaneous rate of change in per unit of C with respect to x when x 100 This is called the marginal cost Its significance will be explained in a future chapter per unit
Calculus
Indefinite IntegrationSubmit Answer DETAILS SCALCET9 2 7 052 8 0 11 Points The quantity in pounds of a gourmet ground coffee that is sold by a coffee company at a price of p dollars per pound is Q f p a What is the meaning of the derivative f 5 What are its units O The rate of change of the quantity of coffee sold with respect to the price per pound when the price is 5 per pound The units are pounds dollars pound O The price of the coffee as a function of the supply The units are pounds O The rate of change of the price per pound with respect to the quantity of coffee sold when the price is 5 per pound The units are dollars pound O The rate of change of the price per pound with respect to the quantity of coffee sold when the price is 5 per pound The units are pounds dollars pound O The rate of change of the quantity of coffee sold with respect to the price per pound when the price is 5 per pound The units are dollars pound b Is f 5 positive or negative Explain O positive O negative
Calculus
Limits & ContinuityThe little rep lim h 0 O f x cos x a cos h 1 h 4 O f x cos x a 0 O f x cos x a O f x cos x a O f x cos x a Need Help Submit Answer velocity 17 TU 3 IT 6 Read It f t 18 DETAILS Watch It 12 0 11 Points A particle moves along a straight line with equation of motion s f t where s is measured in meters and t in seconds Find the velocity and speed in m s when t 4 35 t 1 SCALCET9 2 7 036 m s