Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
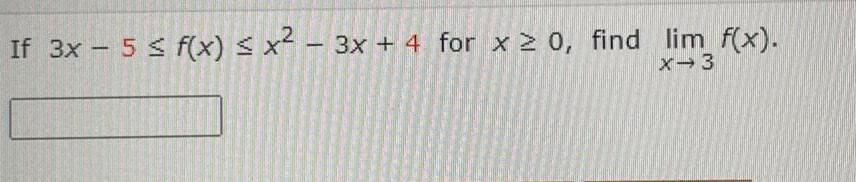
Calculus
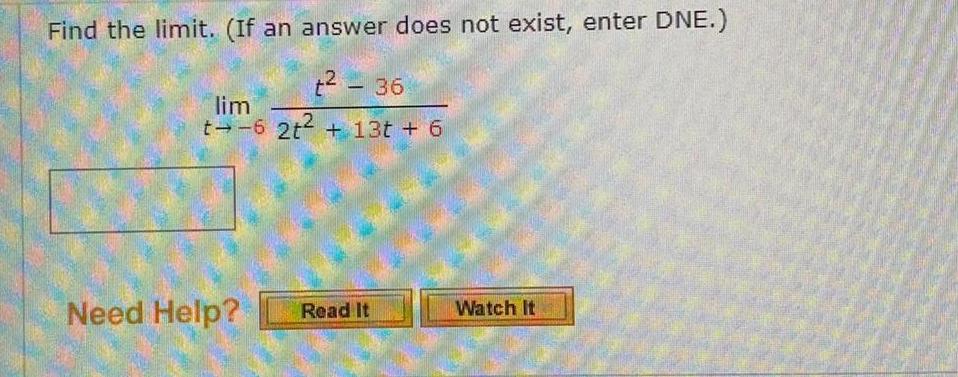
Limits & ContinuityFind the limit If an answer does not exist enter DNE t 36 2t 13t 6 lim t 6 Need Help Read It Watch It
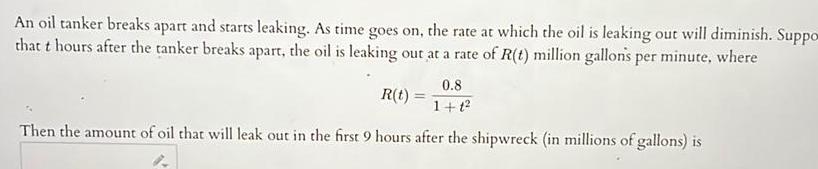
Calculus
Indefinite IntegrationAn oil tanker breaks apart and starts leaking As time goes on the rate at which the oil is leaking out will diminish Suppo that t hours after the tanker breaks apart the oil is leaking out at a rate of R t million gallons per minute where R t 0 8 1 1 Then the amount of oil that will leak out in the first 9 hours after the shipwreck in millions of gallons is

Calculus
Definite IntegralsValues of f x y are shown in the table below x 32 3 32 3 6 y 4 8 y 4 5 10 13 10 12 16 V 5 12 14 7 Let R be the rectangle 3 3 6 4 y 5 Find the values of Riemann sums which are reasonable over and under estimates for f f x y dA with Ar 0 3 and Ay 0 over estimate 5 85 under estimate 6
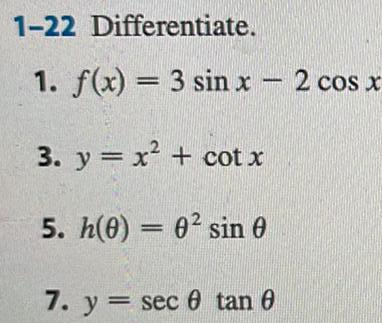
Calculus
Differentiation1 22 Differentiate 1 f x 3 sin x 2 cos x 3 y x cotx 5 h 0 0 sin 0 7 y sec 0 tan 0

Calculus
Definite IntegralsEvaluate the integral Answer 484x 5y Answers A Answer S e42 5y dA R 0 6 x 0 8 5y d
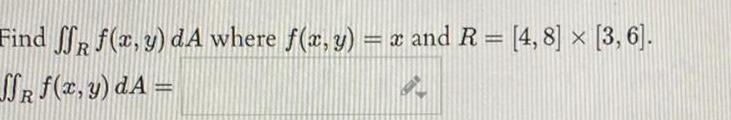
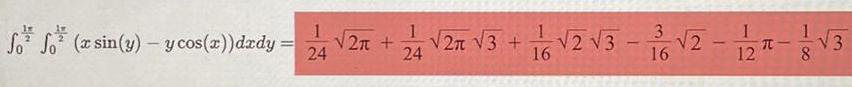
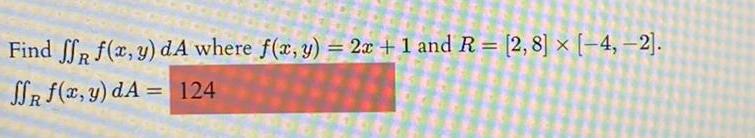
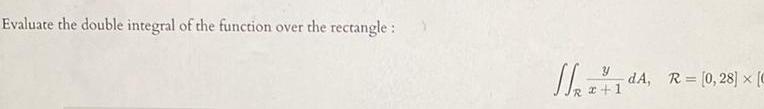
Calculus
DifferentiationEvaluate the double integral of the function over the rectangle Y 1dA R 0 28 x 2 1


Calculus
Application of derivativesUsing Riemann sums with four subdivisions in each direction find upper and lower bounds for the volume under the graph of f x y 1 2zy above the rectangle R with 0 z 1 0 y 3 upper bound lower bound

Calculus
Application of derivativesValues of f x y are shown in the table below x 3x 3 3r 3 6 13 16 y 4 8 10 y 4 5 10 12 y 5 12 14 7 Let R be the rectangle 3 3 6 4 y 5 Find the values of Riemann sums which are reasonable over and under estimates for f f x y dA with Ar 0 3 and Ay 0 over estimate 1 under estimate
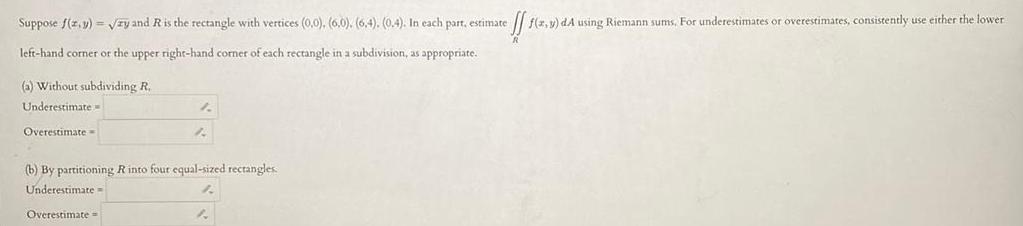
Calculus
Application of derivativesSuppose f z y zy and R is the rectangle with vertices 0 0 6 0 6 4 0 4 In each part estimate effs f x y dA using Riemann sums For underestimates or overestimates consistently use either the lower left hand corner or the upper right hand corner of each rectangle in a subdivision as appropriate a Without subdividing R Underestimate Overestimate 1 A b By partitioning R into four equal sized rectangles Underestimate Overestimate
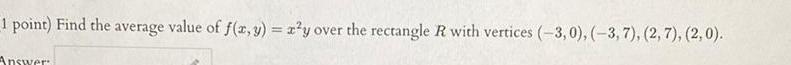
Calculus
Application of derivatives1 point Find the average value of f x y x y over the rectangle R with vertices 3 0 3 7 2 7 2 0 Answer
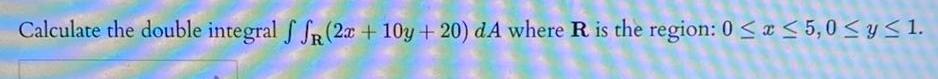
Calculus
Definite IntegralsCalculate the double integral f SR 2x 10y 20 dA where R is the region 0 x 5 0 y 1

Calculus
Application of derivativesValues of f x y are given in the table below Let R be the rectangle 1551 6 25ys 3 2 Find a Riemann sum which is a reasonable estimate for ff z y da with Az 0 2 and Ay 0 4 Note that the values given in the table correspond to midpoints yz 1 1 1 3 1 5 2 2 3 0 5 26 7 5 3 0 7 5 1 4
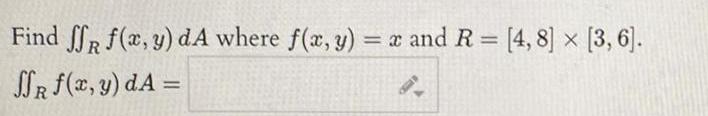
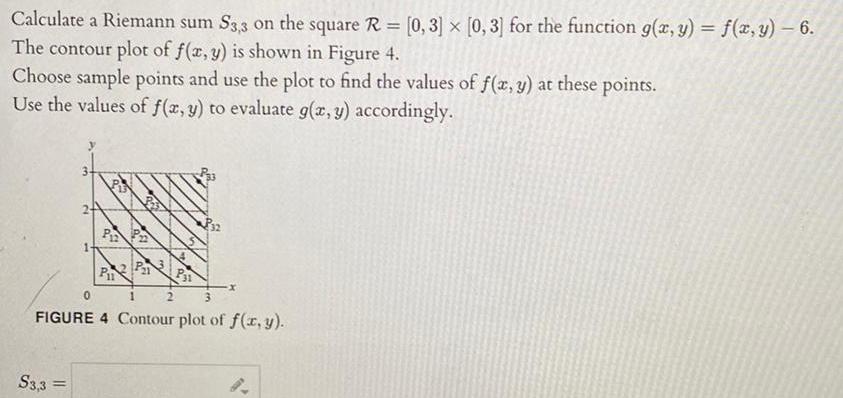
Calculus
Indefinite IntegrationCalculate a Riemann sum S3 3 on the square R 0 3 x 0 3 for the function g x y f x y 6 The contour plot of f x y is shown in Figure 4 Choose sample points and use the plot to find the values of f x y at these points Use the values of f x y to evaluate g x y accordingly S3 3 PP P P21 P31 0 1 3 FIGURE 4 Contour plot of f x y P32 2
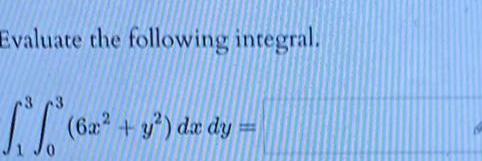
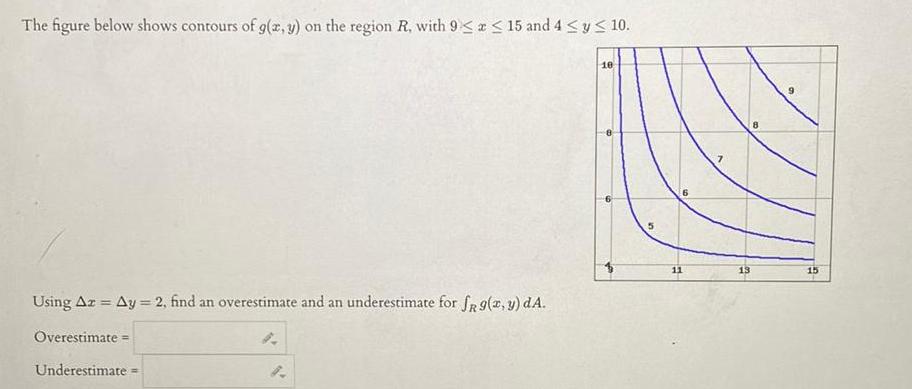
Calculus
Limits & ContinuityThe figure below shows contours of g x y on the region R with 9 x 15 and 4 y 10 Using Az Ay 2 find an overestimate and an underestimate for SR 9 x y dA Overestimate 4 Underestimate 1 10 5 11 15

Calculus
Indefinite IntegrationCompute the Riemann sum S4 3 to estimate the double integral of f x y 6ry over R 1 3 x 1 2 5 Use the regular partition and upper right vertices of the subrectangles as sample points
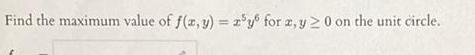
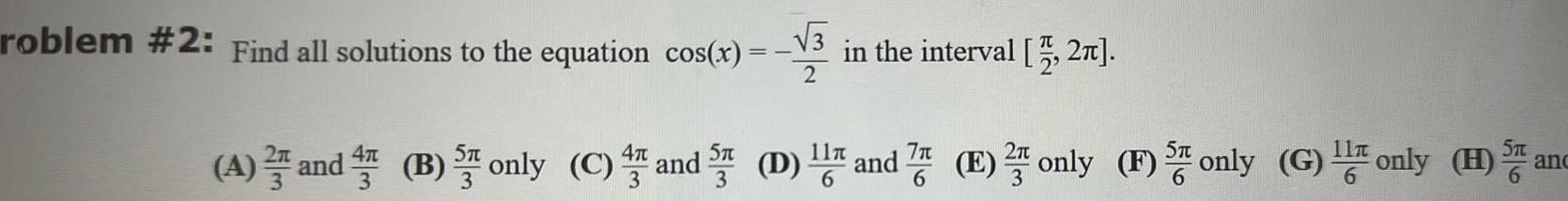
Calculus
Application of derivativesroblem 2 Find all solutions to the equation cos x 3 in the interval 2 5T 4 and A and B only C and 5 D and 7 E only F only G only H I ST
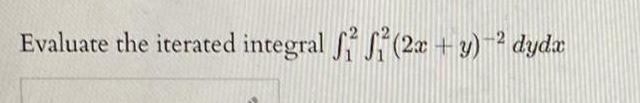
Calculus
Indefinite IntegrationFind the minimum and maximum values of the function f x y x y subject to the given constraint a y 32 fmin

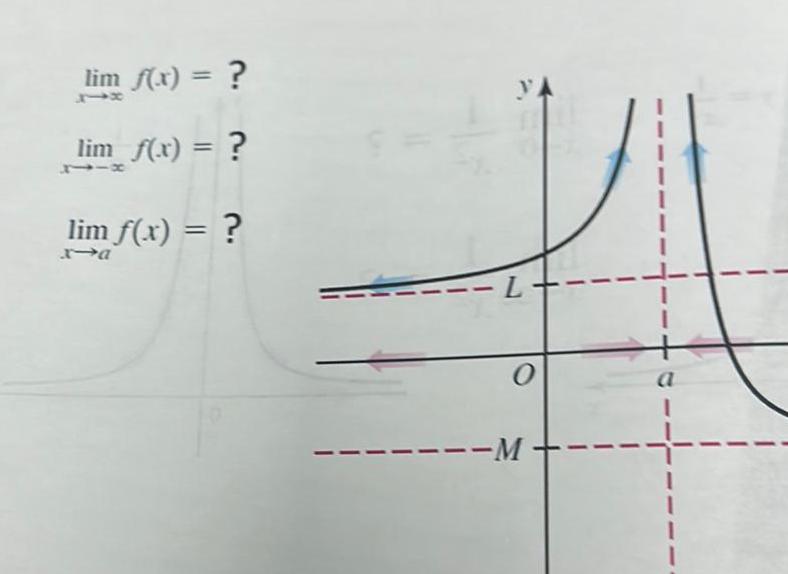
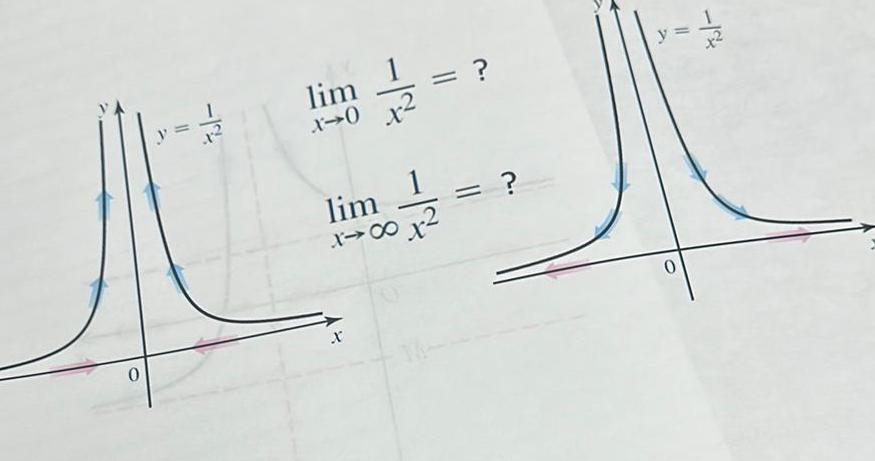
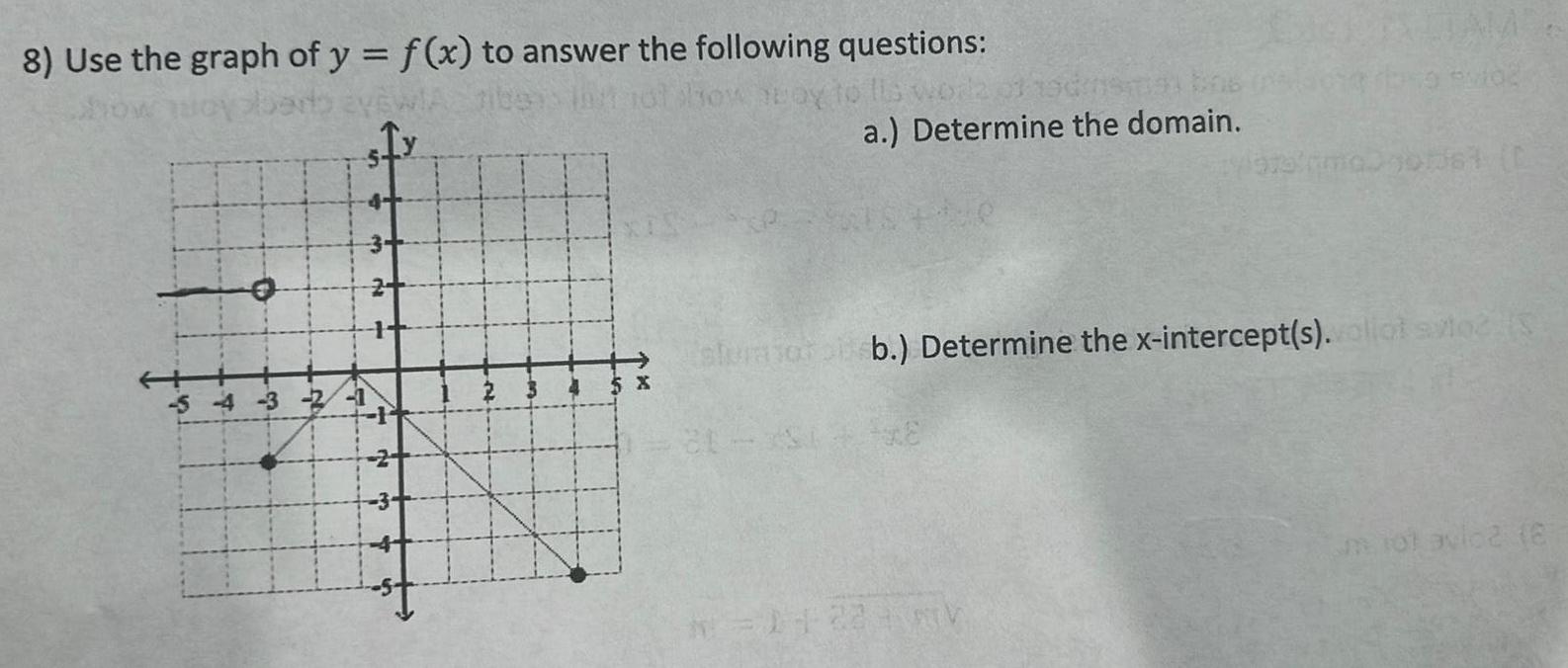
Calculus
Limits & Continuity8 Use the graph of y f x to answer the following questions show away to lis work sfy 5 4 3 2 506 a Determine the domain stumboro b Determine the x intercept s vollot svo S 21 11231 mot avio2 8
Calculus
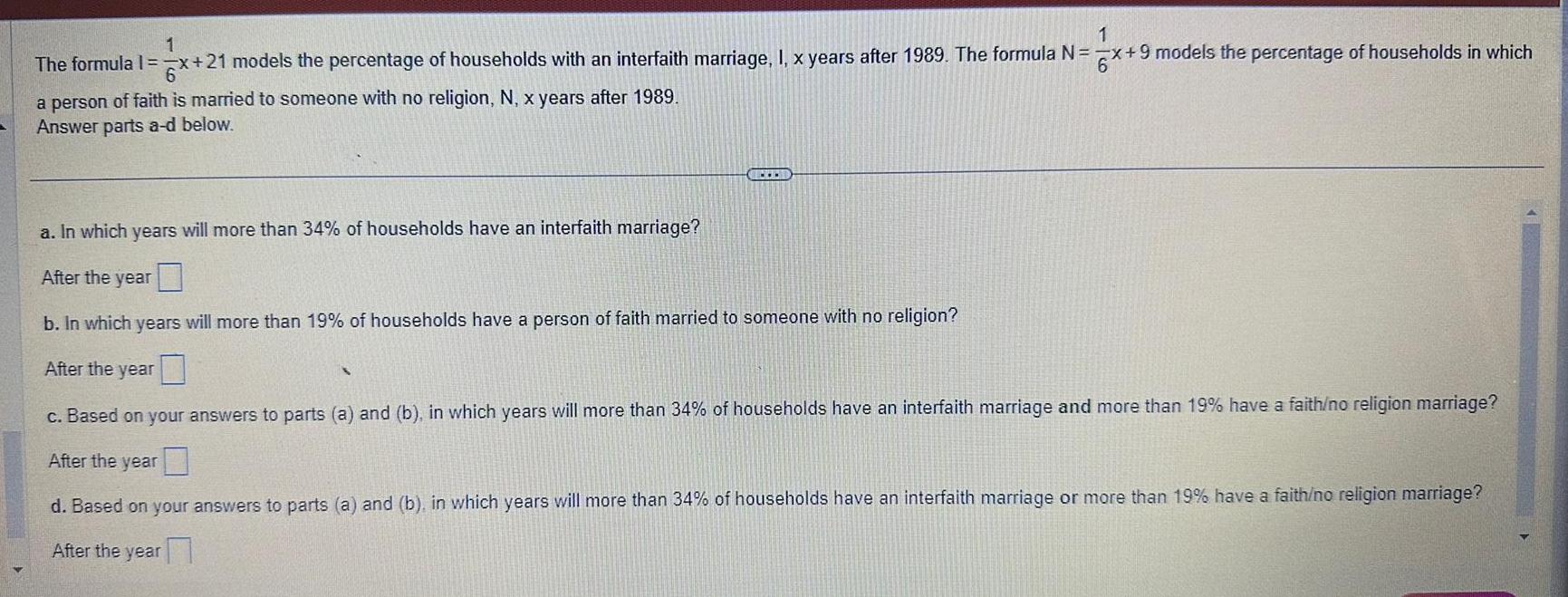
Limits & Continuity1 x 21 models the percentage of households with an interfaith marriage I x years after 1989 The formula N x 9 models the percentage of households in which 1 The formula 1 x 2 a person of faith is married to someone with no religion N x years after 1989 Answer parts a d below a In which years will more than 34 of households have an interfaith marriage After the year b In which years will more than 19 of households have a person of faith married to someone with no religion After the year c Based on your answers to parts a and b in which years will more than 34 of households have an interfaith marriage and more than 19 have a faith no religion marriage After the year d Based on your answers to parts a and b in which years will more than 34 of households have an interfaith marriage or more than 19 have a faith no religion marriage After the year S 16 2025
Calculus
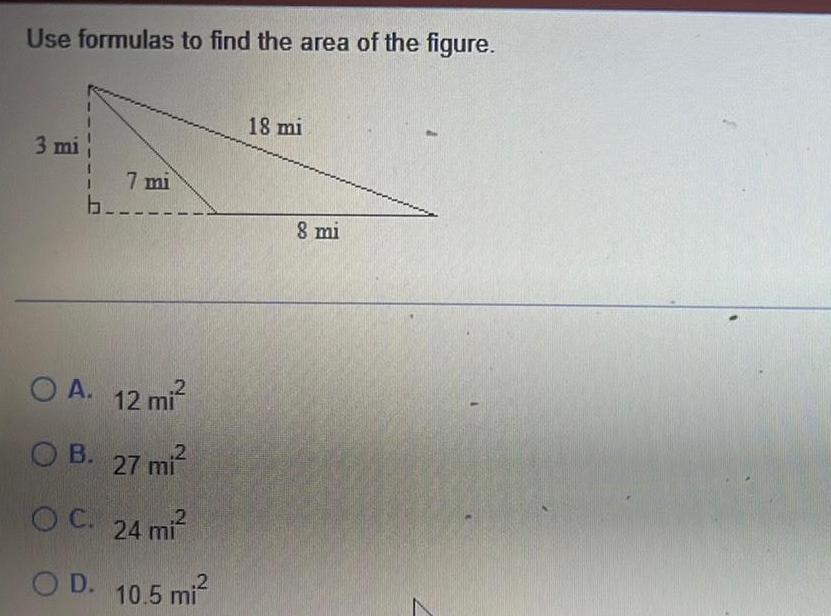
DifferentiationUse formulas to find the area of the figure 3 mi b 7 mi 2 OA 12 mi 2 OB 27 mi OC 24 mi OD 10 5 mi 18 mi 8 mi
Calculus
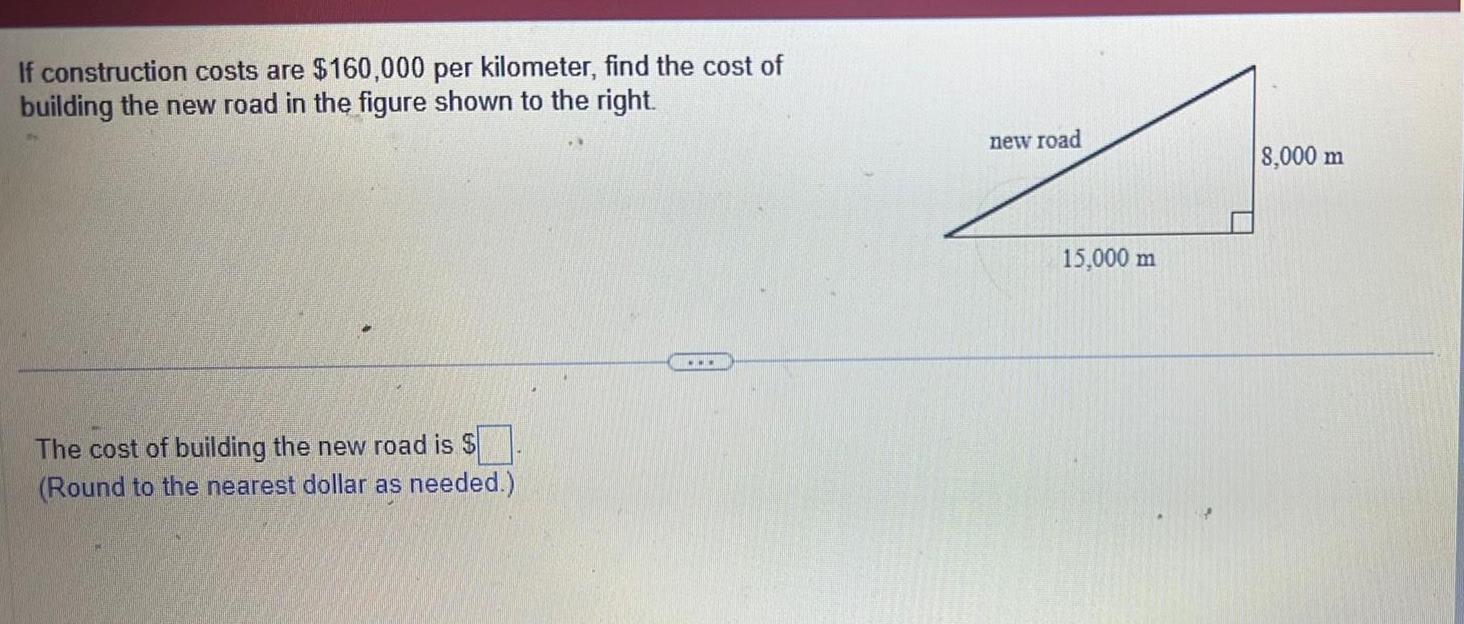
Limits & ContinuityIf construction costs are 160 000 per kilometer find the cost of building the new road in the figure shown to the right The cost of building the new road is Round to the nearest dollar as needed new road 15 000 m 8 000 m

Calculus
Vector CalculusLet f x x x fx 0 S x if x 0 1 I f 0 exists A only I only II C I and II only All of them None of them Which of the following statements are true II lim f x exists III is continuous at x 0 x 0 lim x X 70 x lim x x X 70 o CON SINGE I is when X 0

Calculus
Indefinite IntegrationThis problem asks you to evaluate U X 2 using integration by parts Fill in the table below with the appropriate terms for setting up the integration by parts du 1 dx sin 10x dx a sin 10 da Crain 1 V Now substitute all of this into the Integration by Parts formula giving fas x cos 10x 10 S Complete the last integration to get 10 6 6 dv cos 10x dx cos 10x 10 2 da
Calculus
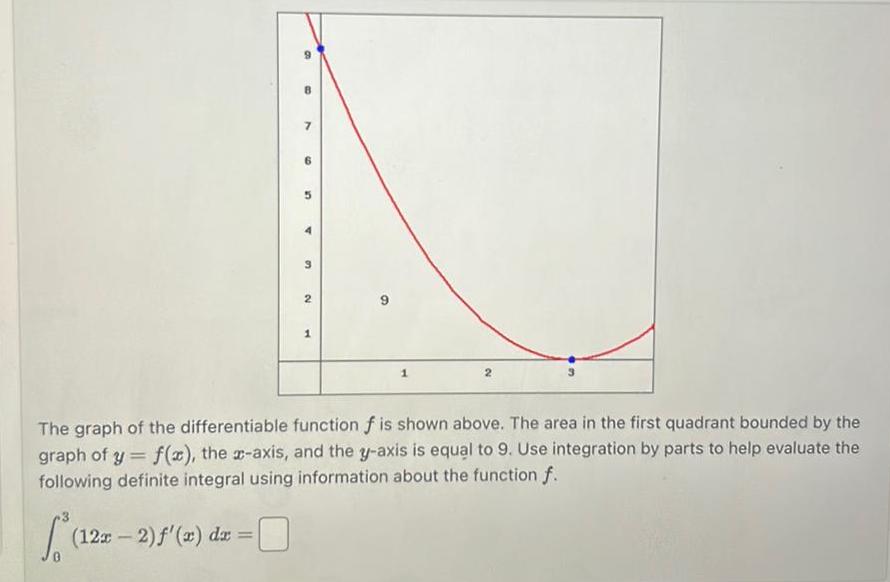
Definite Integrals8 122 12r 2 f x dx 7 6 5 3 2 1 6 1 The graph of the differentiable function f is shown above The area in the first quadrant bounded by the graph of y f x the x axis and the y axis is equal to 9 Use integration by parts to help evaluate the following definite integral using information about the function f
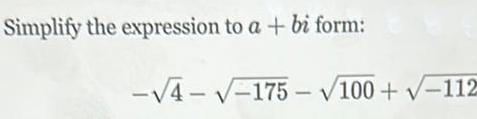

Calculus
Indefinite Integrationx 3 e 8 da using integration by parts Fill in the table below with the appropriate terms for setting up the integration by parts Complete the last integration to get u u 3 du 1 dx dv e 8x dx Now substitute all of this into the Integration by Parts formula giving x 3 e 8 dx x 3 6 V 0 10 dr 3 e 8x da C

Calculus
Vector Calculus21 8 xf x dx 1 7 7 2 7 8 3 4 6 4 10 5 he function f has a continuous second derivative The table above gives values of f and its first erivative at selected values of x Use integration by parts to help evaluate the following definite integral sing data from the table 2
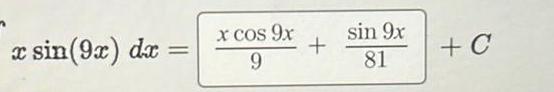
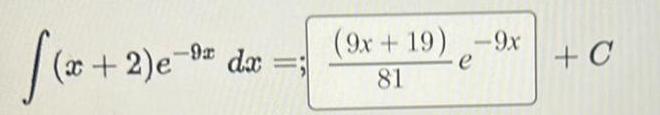
Calculus
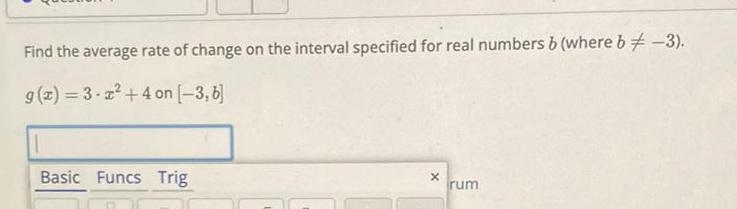
DifferentiationFind the average rate of change on the interval specified for real numbers b where b 3 g x 3 2 4 on 3 6 Basic Funcs Trig X rum

Calculus
Indefinite IntegrationThis problem asks you to evaluate using integration by parts Fill in the table below with the appropriate terms for setting up the integration by parts u Complete the last integration to get 12 du x ln x dx dx V dv Now substitute all of this into the Integration by Parts formula giving x 1 x dx In o do dx 0 10 C da
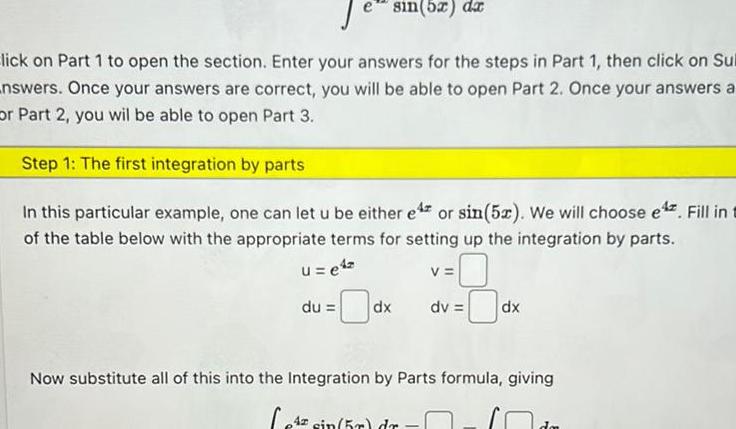
Calculus
Application of derivativese sin 5x dx lick on Part 1 to open the section Enter your answers for the steps in Part 1 then click on Sul answers Once your answers are correct you will be able to open Part 2 Once your answers a or Part 2 you wil be able to open Part 3 Step 1 The first integration by parts In this particular example one can let u be either e or sin 5x We will choose e Fill in t of the table below with the appropriate terms for setting up the integration by parts u e4 du V dx dv 4 sin 5r dr dx Now substitute all of this into the Integration by Parts formula giving
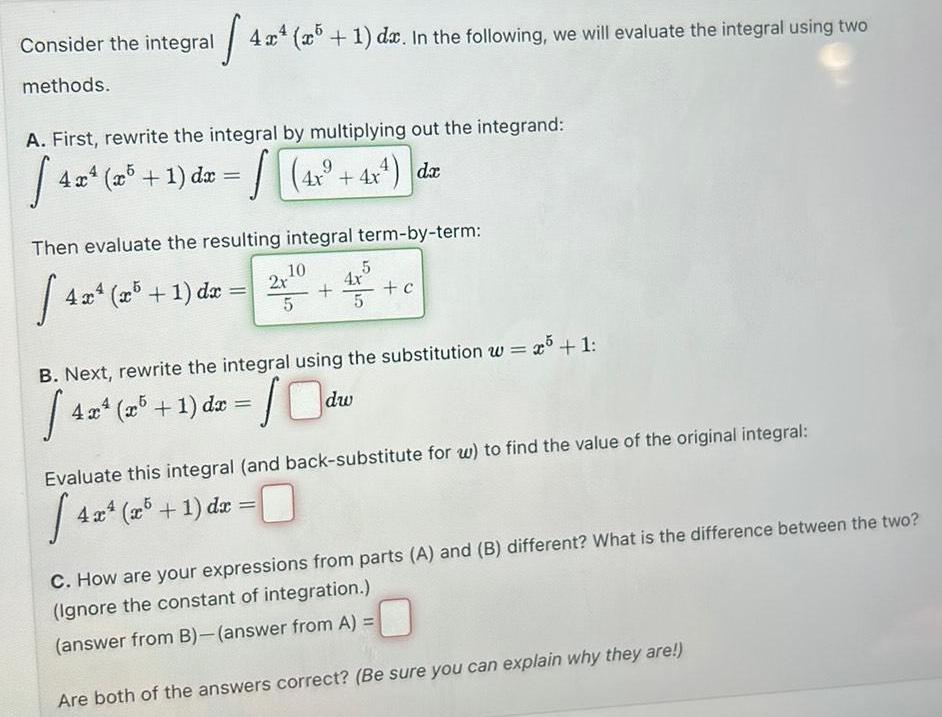
Calculus
Indefinite IntegrationConsider the integral methods 4x 4x4 5 1 dx In the following we will evaluate the integral using two A First rewrite the integral by multiplying out the integrand 9 4 4x4 x 1 dx 4x 4x da Then evaluate the resulting integral term by term 4x4 4x4 xr5 1 dr 10 4x4 x5 1 dx 2x 5 4x4 x5 1 dx x 10dw 5 4x 5 B Next rewrite the integral using the substitution w x5 1 424 25 c Evaluate this integral and back substitute for w to find the value of the original integral 43 C How are your expressions from parts A and B different What is the difference between the two Ignore the constant of integration answer from B answer from A Are both of the answers correct Be sure you can explain why they are

Calculus
Definite Integralss 4x4 5 1 dx In the following we will evaluate the integral using two Consider the integral methods A First rewrite the integral by multiplying out the integrand 40 4x x 1 dx Then evaluate the resulting integral term by term 4x 4 x x5 1 dx da B Next rewrite the integral using the substitution w x5 1 42 10dw 4x x5 1 dx Evaluate this integral and back substitute for w to find the value of the original integral 14 4x4 x5 1 dx C How are your expressions from parts A and B different What is the difference between the two Ignore the constant of integration answer from B answer from A

Calculus
Definite IntegralsUsing the method of u substitution 4 S 6x 8 dx 2 where U du a b f u S f f u du enter a function of x dx enter a function of x enter a number enter a number enter a function of u The value of the original integral is

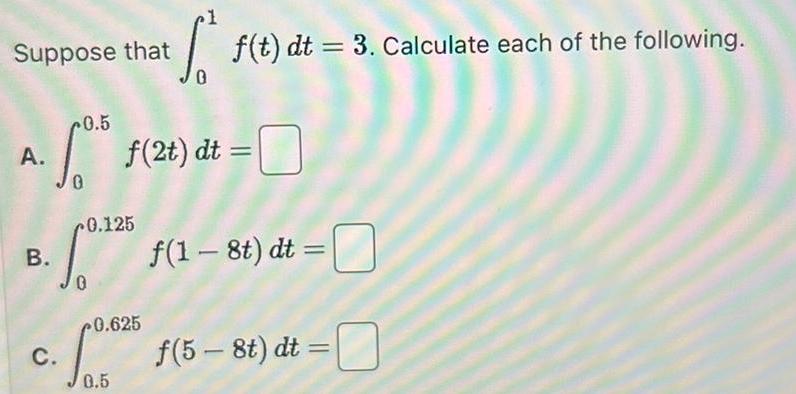
Calculus
Vector CalculusSuppose that A So f 2t dt B 0 125 C 0 625 S05 0 5 f t dt 3 Calculate each of the following f 1 8t dt f 5 8t dt

Calculus
Application of derivativesEvaluate the integral using an appropriate substitution 9e9e T dx c C