Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
Vector CalculusFind the x and y intercepts of the graph of the equation If an answer does not exist enter DNE 9x 4y 36 x intercept x intercept x y y intercept x y y intercept x y x y b x xy 5y 81 x intercept x y x intercept x y y intercept x y smaller x value larger x value smaller y value larger y value smaller x value larger x value

Calculus
Application of derivativesLet f x y x y and c t t 2t a Calculate Vf c t B b Use the Chain Rule for Paths to evaluate f c t at t 1 f c 1
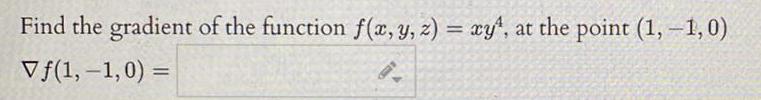
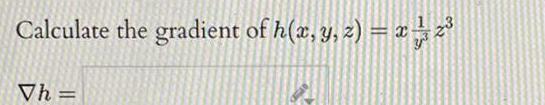
Calculus
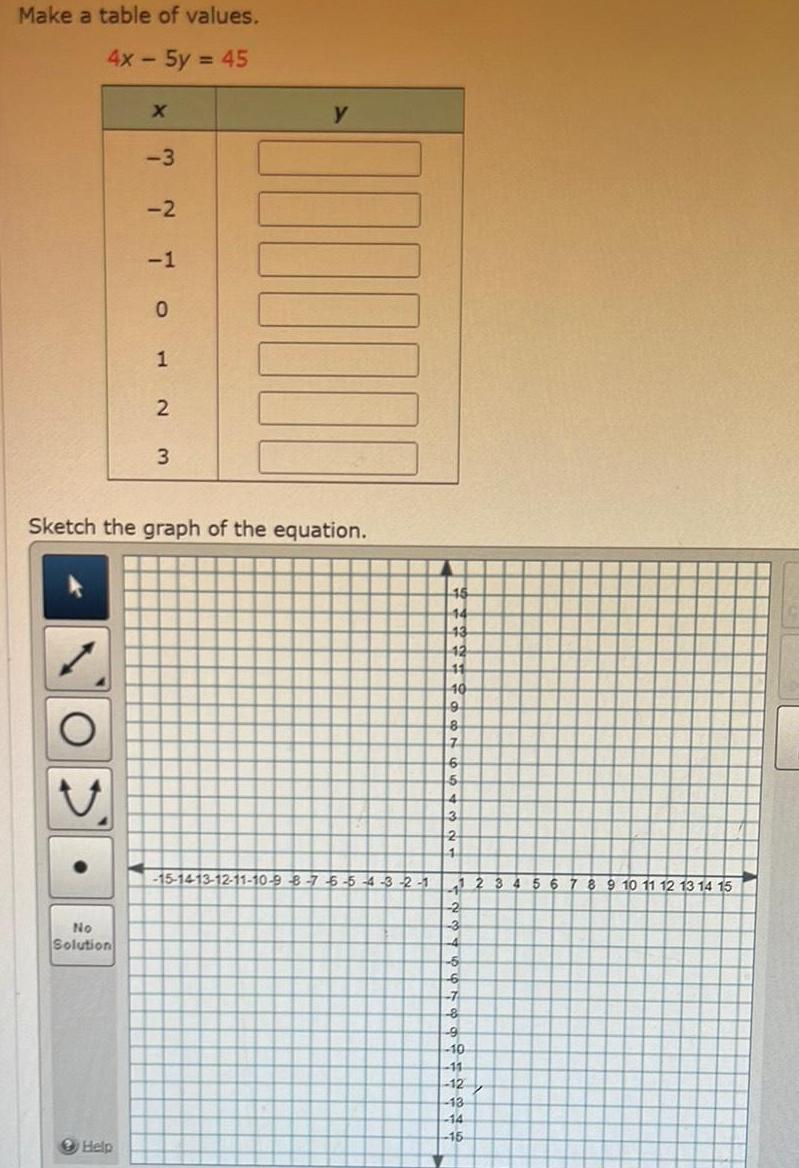
Limits & ContinuityMake a table of values 4x 5y 45 No Solution X Help 3 2 1 0 1 2 3 Sketch the graph of the equation y 15 1413 12 11 10 9 8 7 6 5 4 3 2 1 H 15 14 43 12 11 40 9 8 7 6 5 4 3 2 1 1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 2 3 4 5 6 7 8 9 10 11 12 13 14 15

Calculus
Application of derivativesFind an equation of the circle that satisfies the given conditions Center at the origin passes through 5 8

Calculus
Differential equationsInstructions Use algebraic techniques to solve problems unless otherwise instructed Show the calcula to your answers except basic arithmetic when there is work to show Simplify and circle your final ans 1 8 pts Consider the equation 4x 4y 4x 24y 37 36 a What is the standard form of the equation of the circle Also find the coordinates of the cen radius and the diameter of the circle 2 2 4x 4y 4x 24y 37 36 4 x y x y 36 37 4 x y2 x 6y 1 2 x y x y XX 2 1 1 y by 9 x 1 y 3 9 2 center b1 3 2 padus 13 Diam 2xradius b 4 pts Sketch a graph of the circle 2x 3 E

Calculus
Application of derivativesA spherical balloon with radius r inches has volume V r r Find a function that represents the amount of air required to inflate the balloon from a radius of r inches to a radius of r 1 inches
Calculus
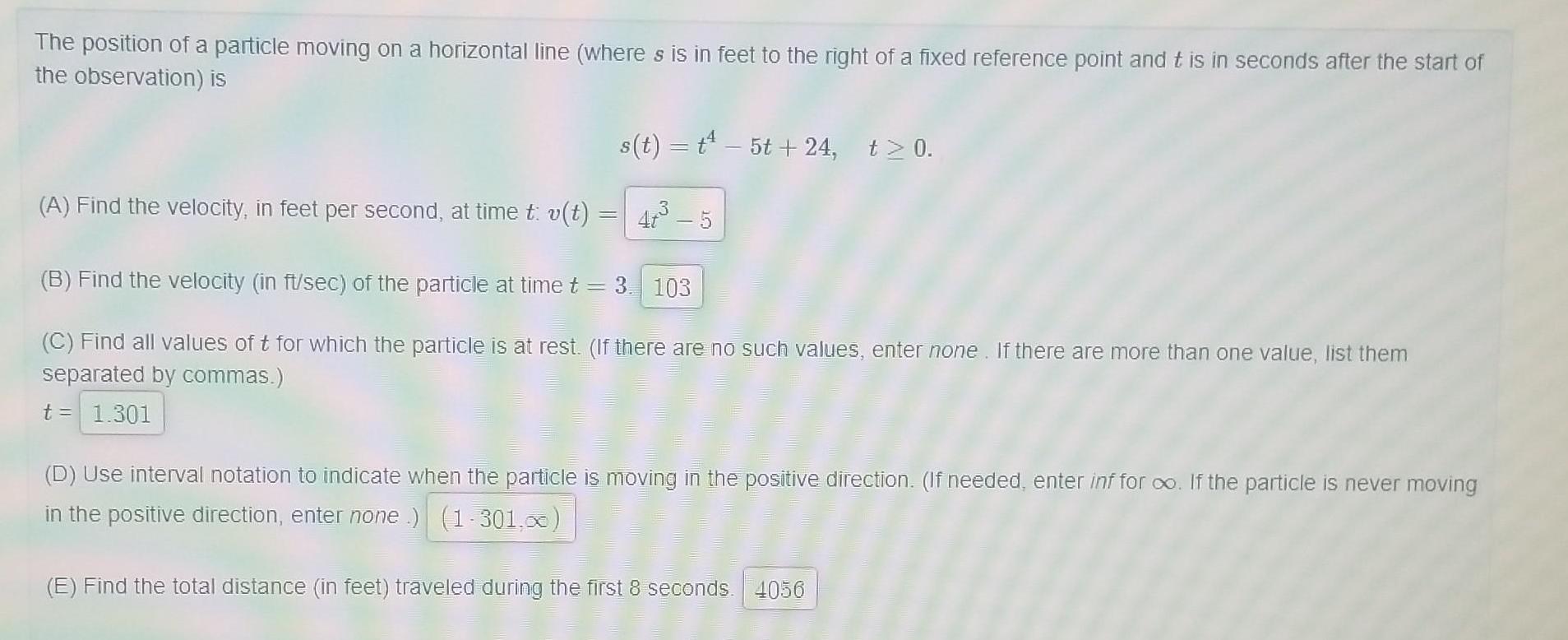
Application of derivativesThe position of a particle moving on a horizontal line where s is in feet to the right of a fixed reference point and t is in seconds after the start of the observation is s t t 5t 24 t 0 3 A Find the velocity in feet per second at time t v t 4 5 B Find the velocity in ft sec of the particle at time t 3 103 C Find all values of t for which the particle is at rest If there are no such values enter none If there are more than one value list them separated by commas t 1 301 D Use interval notation to indicate when the particle is moving in the positive direction If needed enter inf for oo If the particle is never moving in the positive direction enter none 1 301 00 E Find the total distance in feet traveled during the first 8 seconds 4056
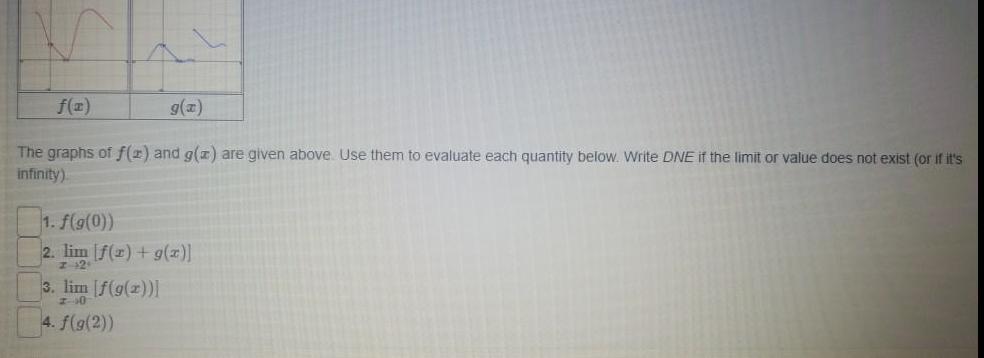
Calculus
Limits & Continuityf x The graphs of f x and g z are given above Use them to evaluate each quantity below Write DNE if the limit or value does not exist or if it s infinity g x 1 f g 0 2 lim f x g x z 2 3 lim f g x 20 4 f g 2
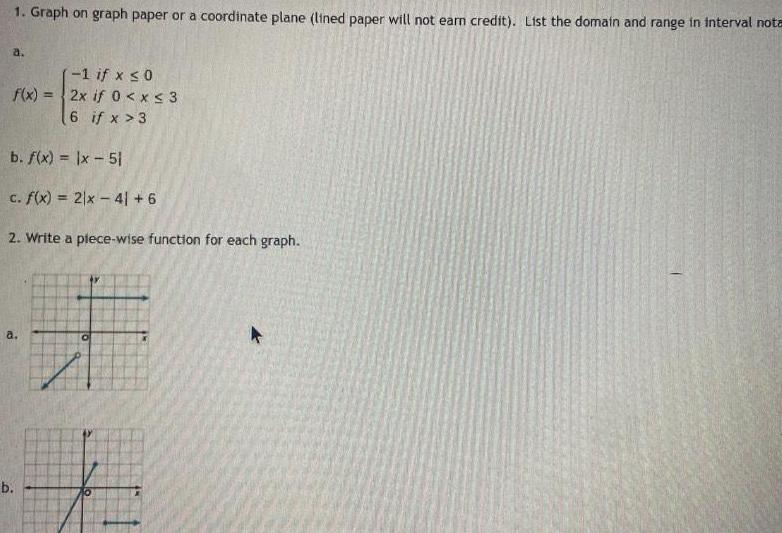
Calculus
Application of derivatives1 Graph on graph paper or coordinate plane lined paper will not earn credit List the domain and range in interval nota a f x b f x x 51 c f x 2x 41 6 2 Write a plece wise function for each graph a b 1 if x 0 2x if 0 x 3 6 if x 3 0
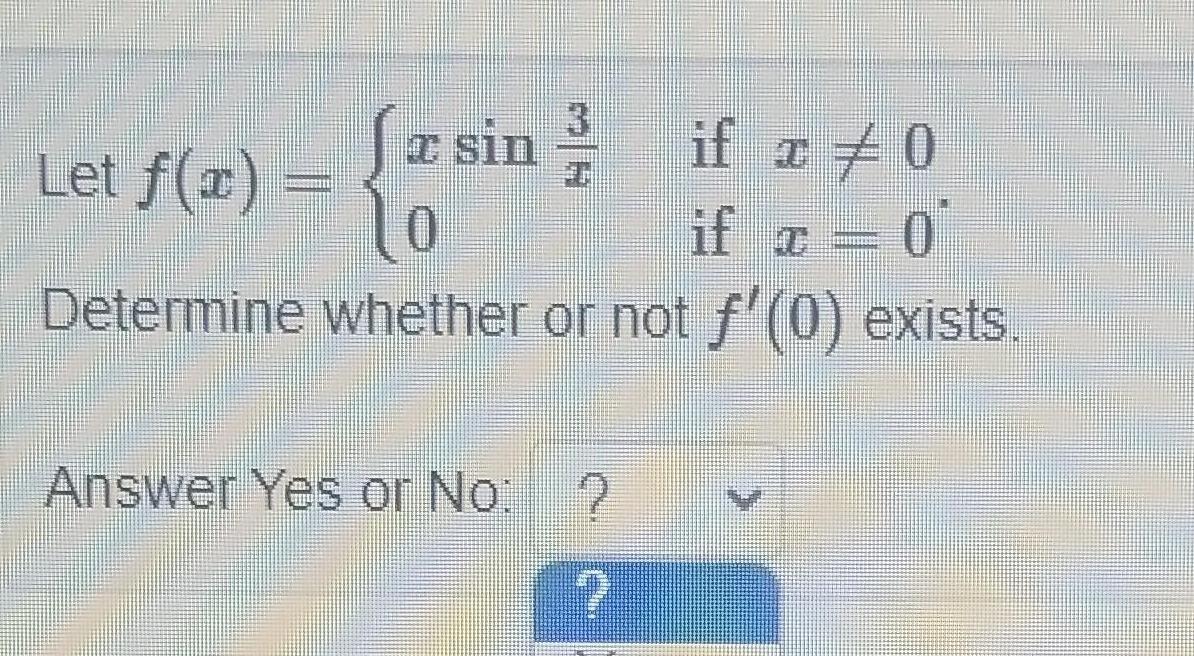
Calculus
Application of derivatives3 Jasin if x 0 z sin if x 0 Determine whether or not f 0 exists Let f 1 Answer Yes or No
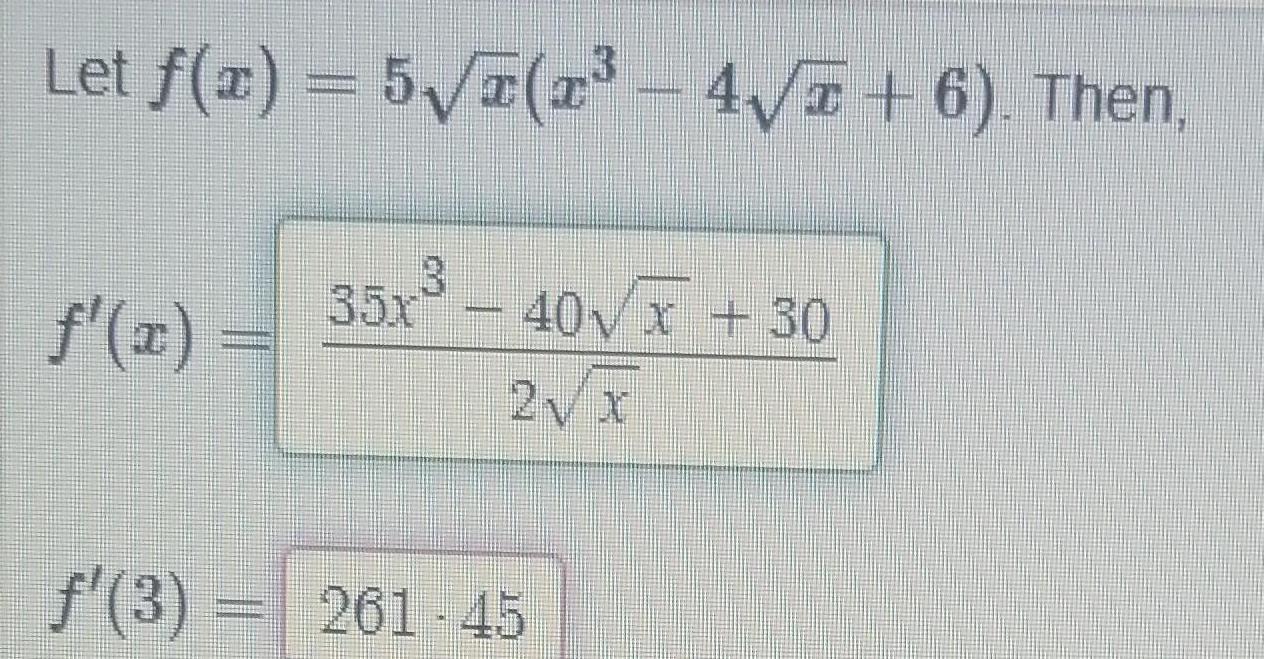

Calculus
Application of derivativesIf a ball is thrown vertically upward from the roof of 32 foot building with a velocity of 48 ft sec its height after t seconds is s t 32 48t 16t a What is the maximum height the ball reaches Answer 80ft b What is the velocity of the ball when it hits the ground height 0 Answer 48
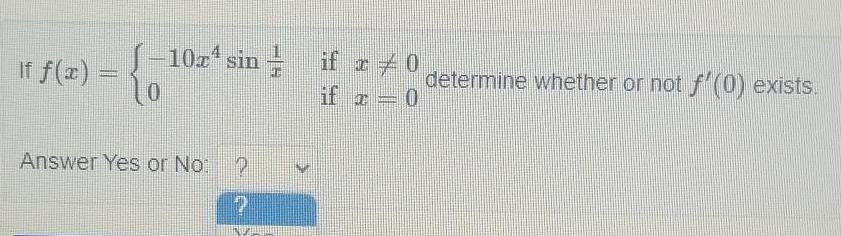
Calculus
DifferentiationIf f x 0 10z sin determine whether or not f 0 exists 0 Answer Yes or No 2 if x if x

Calculus
DifferentiationThe limit f x lim hs0 0 2 h h is the standard expression defining the derivative of some function f x at some number a Find and a 4

Calculus
Application of derivativesLet h x 7 2x Use this to find the equation of the tangent line to the curve y 7 2 at the point 1 5 and write your answer in the form y mx b where m is the slope and b is the y intercept h 1


Calculus
Limits & ContinuityThe limit 81 h 9 h lim h 0 is the standard expression defining the derivative of some function f x at some number a Find f and a f x a
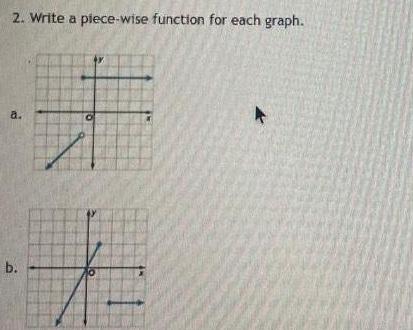

Calculus
Application of derivativesFor the following exercises find the domain of each function expressing answers using Interval notation 3 4 5 2 3x 2 x 3 f x 4x 12 x 4


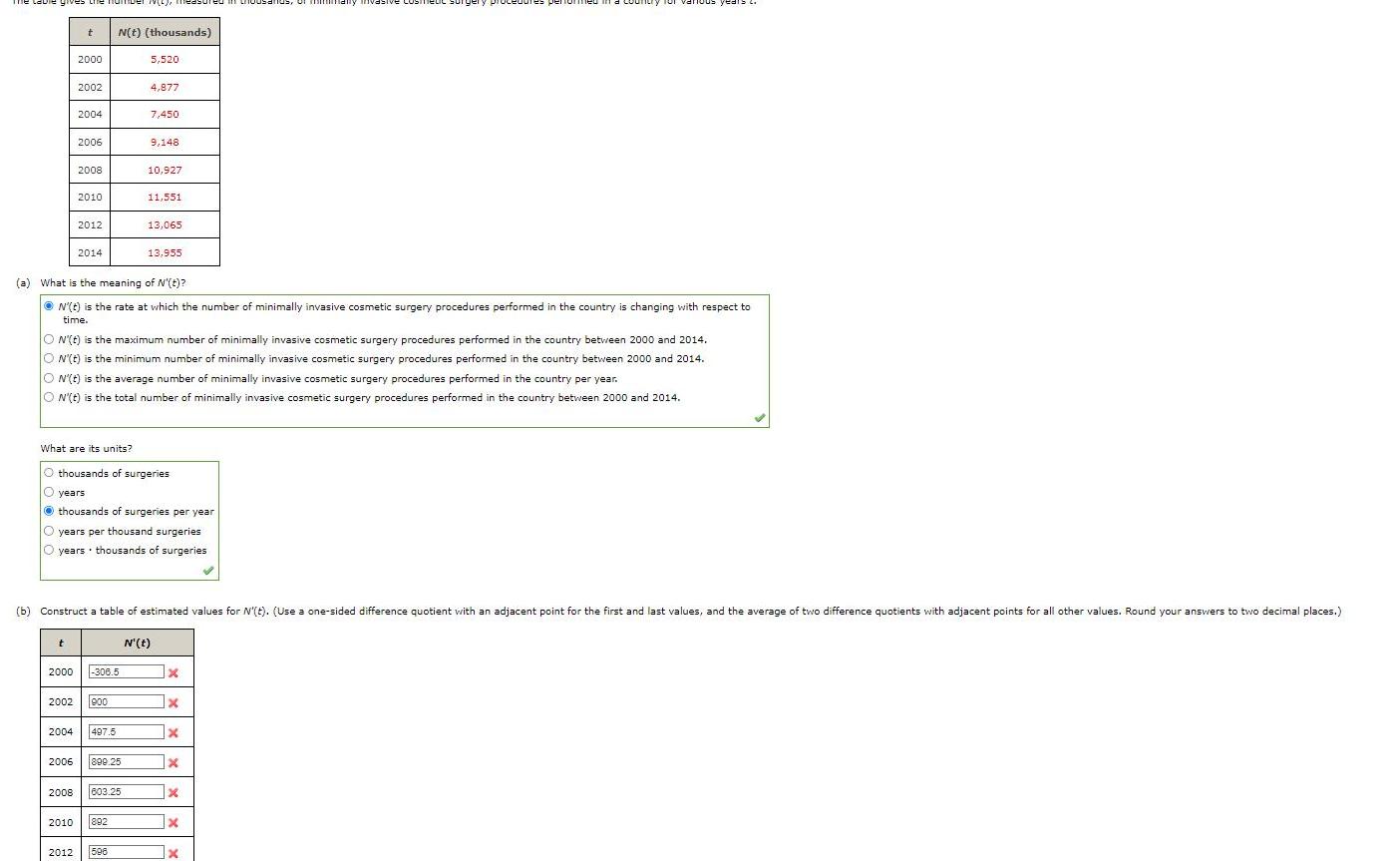
Calculus
DifferentiationLabie gives the number w Q d t 2000 2002 2004 t 2006 2008 2010 2012 2014 N t thousands 2000 306 5 2002 900 2004 497 5 2006 899 25 5 520 2008 603 25 2010 892 4 877 7 450 What are its units O thousands of surgeries years thousands of surgeries per year years per thousand surgeries O years thousands of surgeries 2012 596 a What is the meaning of N t N t is the rate at which the number of minimally invasive cosmetic surgery procedures performed in the country is changing with respect to time 9 148 10 927 O N t is the maximum number of minimally invasive cosmetic surgery procedures performed in the country between 2000 and 2014 ON t is the minimum number of minimally invasive cosmetic surgery procedures performed in the country between 2000 and 2014 ON t is the average number of minimally invasive cosmetic surgery procedures performed in the country per year ON t is the total number of minimally invasive cosmetic surgery procedures performed in the country between 2000 and 2014 11 551 13 065 b Construct a table of estimated values for N t Use a one sided difference quotient with an adjacent point for the first and last values and the average of two difference quotients with adjacent points for all other values Round your answers to two decimal places 13 955 N t 1x x 1x x in thousands of many invasive CUST x euc surgery x various yea x

Calculus
Application of derivativesConsider the following matrix A and it s inverse A 1 2 1 1 2 1 2 By hand calculate the condition number of A using the infinity norm 1 5 2 3 2 1 2
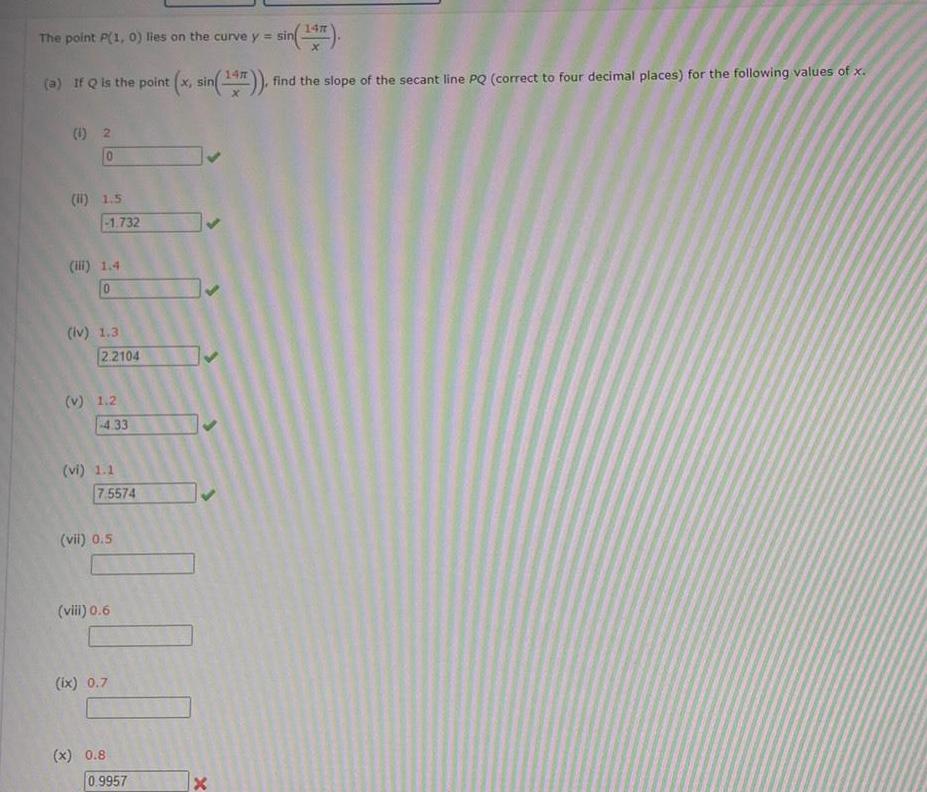
Calculus
Application of derivativeslies on the curve y sin 147 a If Q is the point x sin 147 find the slope of the secant line PQ correct to four decimal places for the following values of x The point P 1 0 1 2 0 1 1 5 1 732 1 4 0 iv 1 3 2 2104 v 1 2 4 33 vi 1 1 7 5574 vii 0 5 viii 0 6 ix 0 7 x 0 8 0 9957 x

Calculus
Limits & ContinuityFind the limit 19 lim 8 X 8 1 x2 A x2 7x 3 x x3 6x2 4 20 lim A 00 B 8 B 314 C 1 C 1 8 1 D D 0
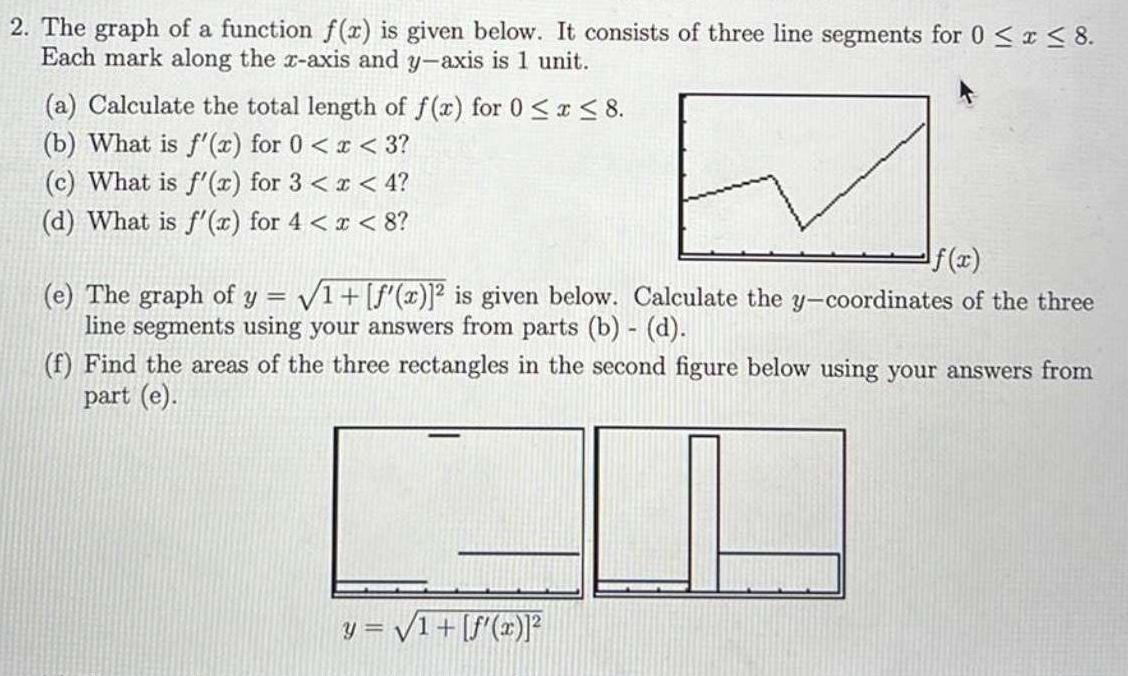
Calculus
Application of derivatives2 The graph of a function f x is given below It consists of three line segments for 0 x 8 Each mark along the x axis and y axis is 1 unit a Calculate the total length of f x for 0 x 8 b What is f x for 0 x 3 c What is f x for 3 x 4 d What is f x for 4 x 8 f x e The graph of y 1 f x 2 is given below Calculate the y coordinates of the three line segments using your answers from parts b d f Find the areas of the three rectangles in the second figure below using your answers from part e y 1 f x

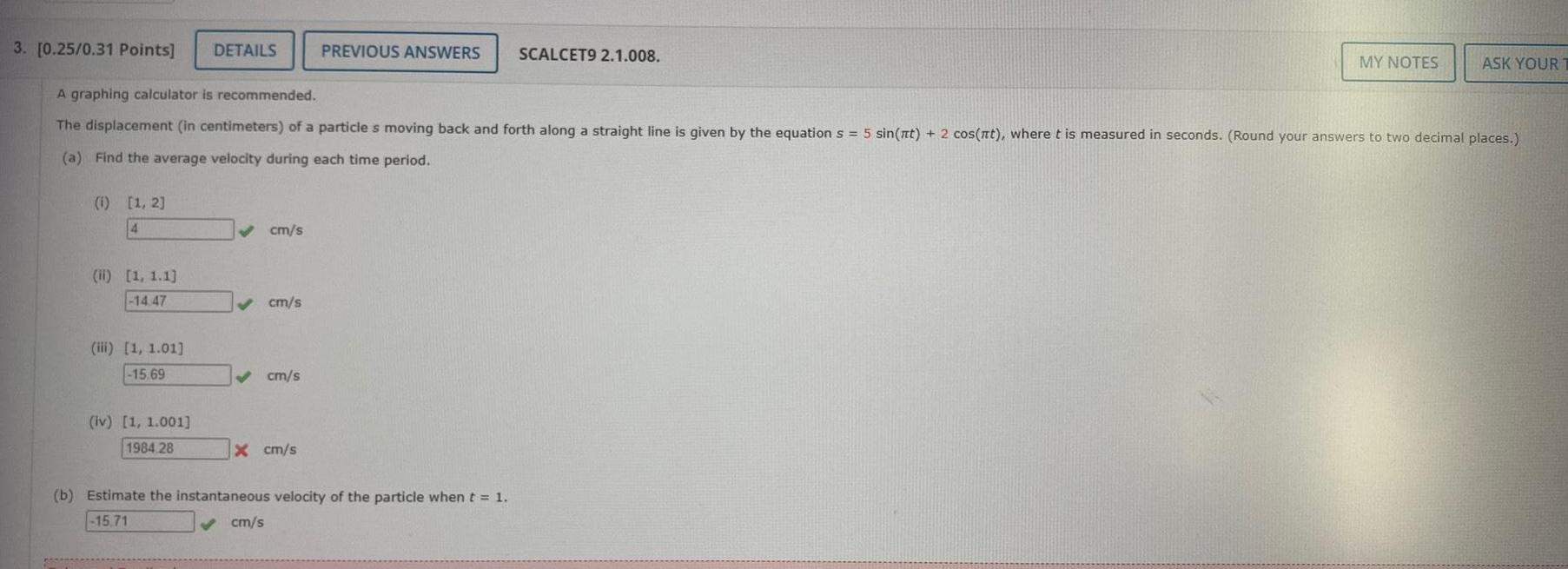
Calculus
Application of derivatives3 0 25 0 31 Points DETAILS 1 1 2 4 A graphing calculator is recommended The displacement in centimeters of a particle s moving back and forth along a straight line is given by the equation s 5 sin nt 2 cos nt where t is measured in seconds Round your answers to two decimal places a Find the average velocity during each time period ii 1 1 1 14 47 iii 1 1 01 15 69 iv 1 1 001 1984 28 cm s cm s cm s x cm s PREVIOUS ANSWERS SCALCET9 2 1 008 cm s b Estimate the instantaneous velocity of the particle when t 1 15 71 MY NOTES ASK YOUR
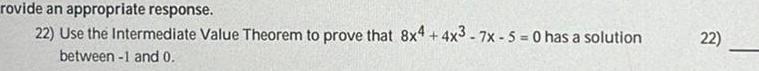
Calculus
Application of derivativesrovide an appropriate response 22 Use the Intermediate Value Theorem to prove that 8x4 4x3 7x 5 0 has a solution between 1 and 0 22

Calculus
Application of derivativesCalculate the derivative of the function by using the formula f x Lim h 0 26 g x 3x2 4x A g x 6x 27 f x 8 X 8 A f x x2 B g x 6x 4 B f x 8 f x h f x h C g x 2x 4 C f x 8x2 D g x 3x 4 D f x 8 x2

Calculus
Limits & ContinuityIn 2003 the first complete human genome was sequenced Based on data from the National Human Genome Research Institute 4 the cost of sequencing a human genome in January 2004 was roughly 29 million For the next few years the cost of sequencing a human genome fell by roughly 15 every 6 months a Using this information write a function E t for the cost to sequence a human genome in millions of dollars t years after January 2004 b Using just the information in the problem and not your answer to a what is E 0 What is E 0 5 Check that the function you wrote in a agrees with this If this exponential trend had continued indefinitely 5 in what year would you expect the price of sequencing a human genome to fall below 1 000 6 Please give an exact answer and then use a calculator to give a decimal approximation for this value

Calculus
Differentiationa b C Find z if a 2 log 4 log 5 log 10 log b log 30 log 52 log c log 8 log a log a d log x 2 log 4 log 3x e log x 1 log 3 log x f ln x 1 1 86 log mn m logs TL log m log m log m log n log m log n alog m log if and only if d e f 711 11
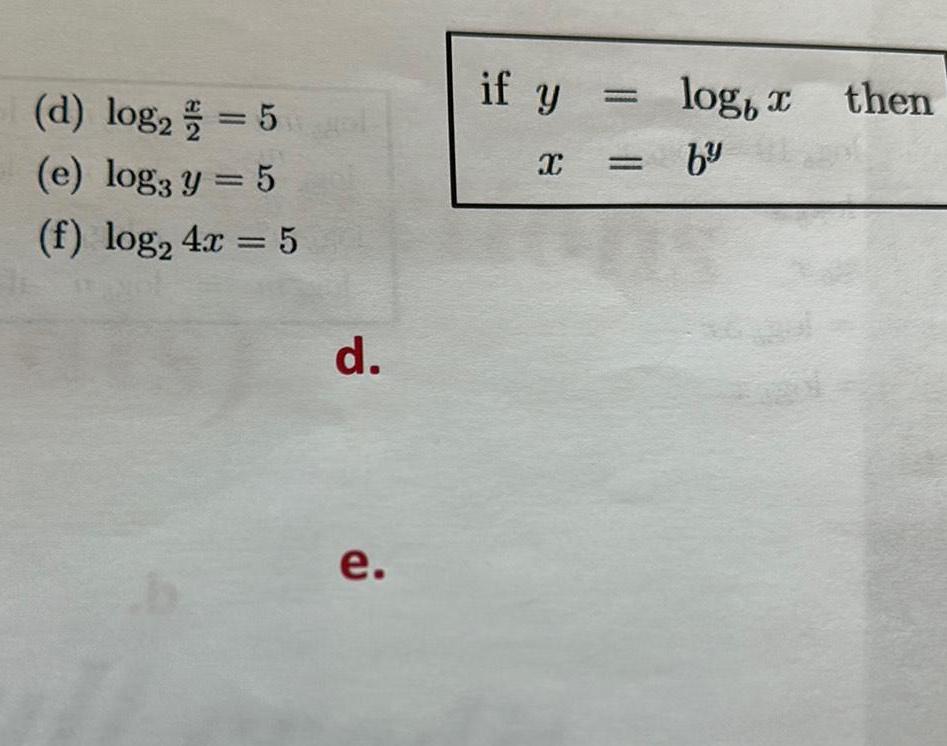

Calculus
Vector Calculus2 Write the equation of the following line in 4x 3y 8 a Slope intercept form b Point slope form

Calculus
Application of derivativesFind a function whose graph is a parabola with vertex 1 5 and that passes through the point 5 11
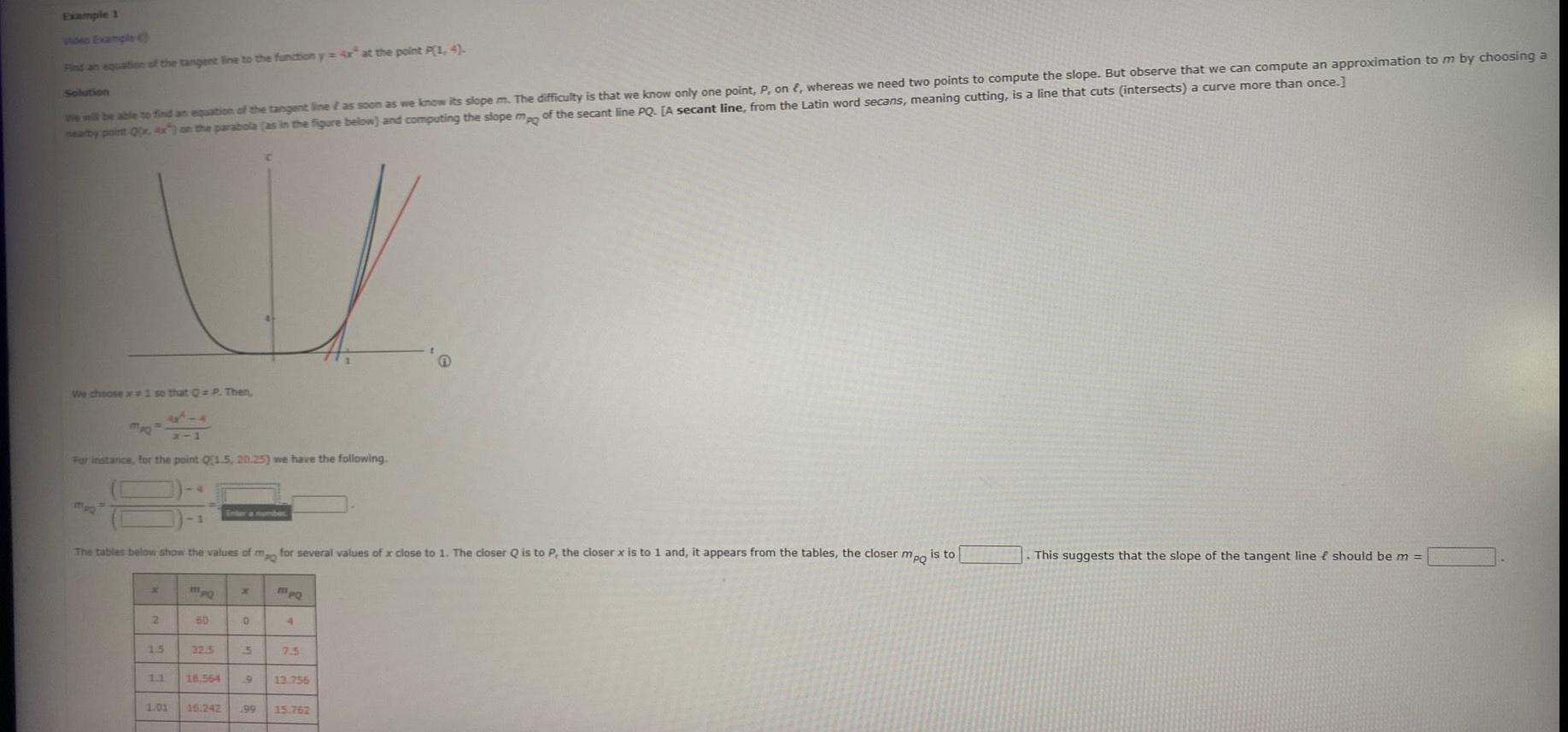
Calculus
DifferentiationExample 1 Find an equation of the tangent line to the function y at the point P 1 4 Solution We will be able to find an equation of the tangent line as soon as we know its slope m The difficulty is that we know only one point P on whereas we need two points to compute the slope But observe that we can compute an approximation to m by choosing a nearby point Q x 4x on the parabola as in the figure below and computing the slope mpo of the secant line PQ A secant line from the Latin word secans meaning cutting is a line that cuts intersects a curve more than once We choose 1 so that Q P Then mpQ For instance for the point Q1 5 20 25 we have the following The tables below show the values of mo for several values of x close to 1 The closer Q is to P the closer x is to 1 and it appears from the tables the closer mpo is to x 2 1 5 1 1 MpQ 50 32 5 18 564 0 5 1 01 16 242 199 MpQ 4 7 5 13 756 15 762 This suggests that the slope of the tangent line f should be m
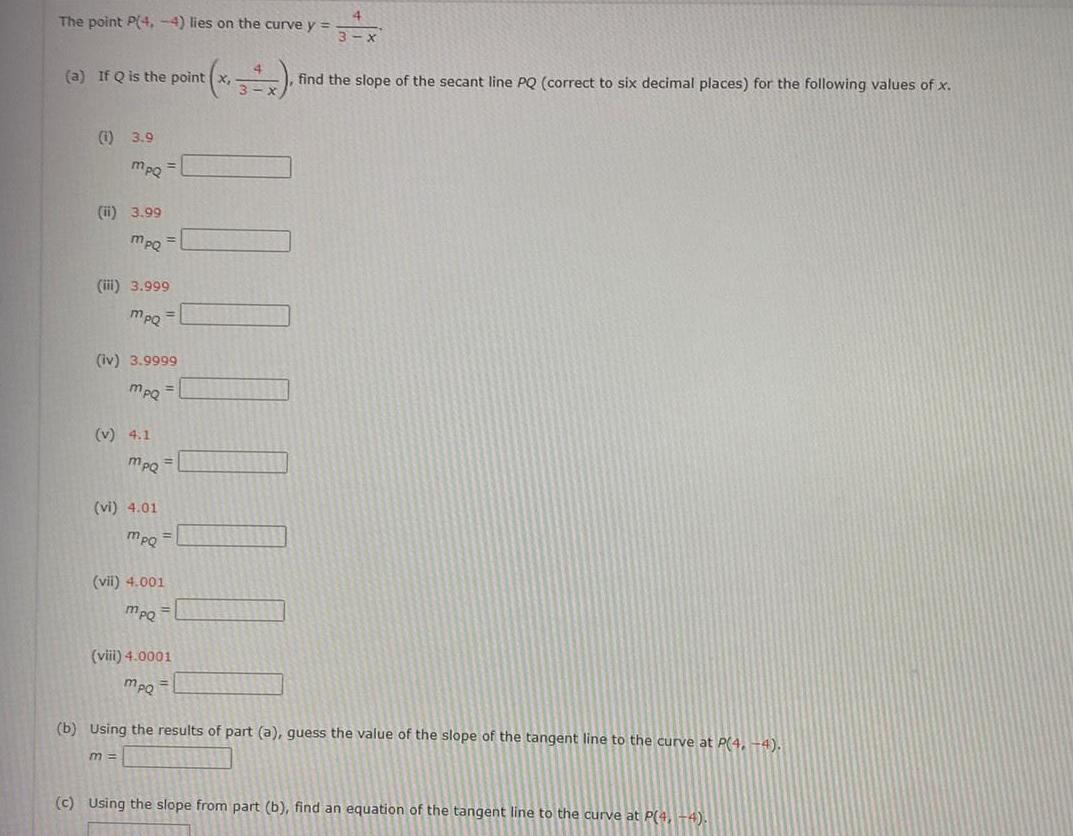
Calculus
Vector CalculusThe point P 4 4 lies on the curve y a If Q is the point 1 3 9 mpqQ ii 3 99 mpQ iii 3 999 mpQ iv 3 9999 MpQ 1 v 4 1 MpQ vi 4 01 m mpQ vii 4 001 mpo viii 4 0001 mpo 4 3 x find the slope of the secant line PQ correct to six decimal places for the following values of x b Using the results of part a guess the value of the slope of the tangent line to the curve at P 4 4 c Using the slope from part b find an equation of the tangent line to the curve at P 4 4


Calculus
Limits & ContinuityRewrite using only positive rational exponents 5x 3yz 4 3 5x 3yz Type a single expression raised to a positive expon


Calculus
Application of derivativesUse the laws of exponents to simplify 3 4 3 3 3 8 3 3 8 3 Simplify your answer Type exponential notation with posit

Calculus
Application of derivativesRewrite with positive exponents 7x 1 8 1 7x Type exponential notation with positive exponents Use integers any numbers in the expression

Calculus
Limits & ContinuityRewrite without rational exponents and simplify if possible 1 6 Simplify your answer Type an exact answer using radicals as nee



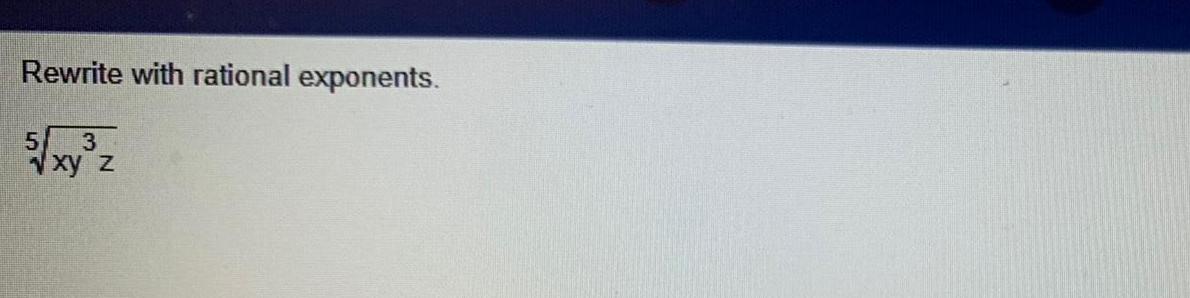
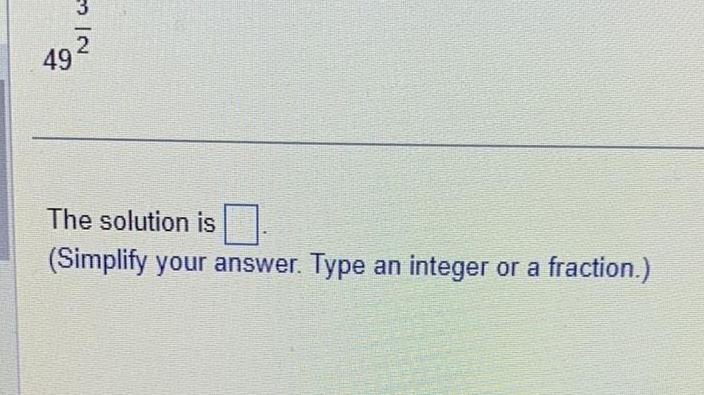
Calculus
Application of derivatives49 The solution is Simplify your answer Type an integer or a fraction