Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
Application of derivativesSimplify by taking roots of the numerator and denominator 64 81 64 81 Type an exact answer using radicals as needed

Calculus
DifferentiationDivide Then simplify by taking roots if possible Assume that all expressions under radicals represent positive numbe 40521 25 5x 7 17 21 25 405x y
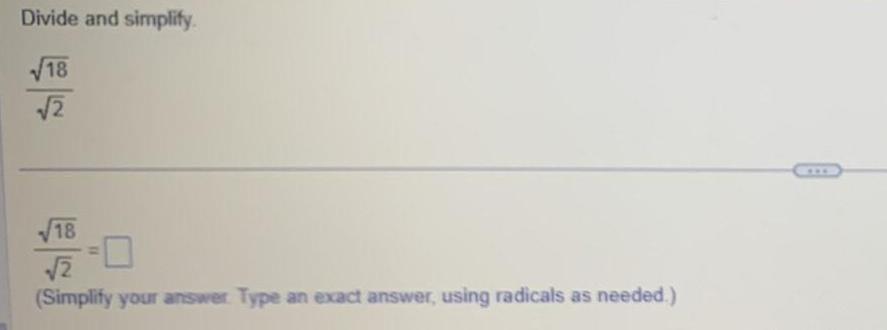
Calculus
Limits & ContinuityDivide and simplify 18 2 18 2 Simplify your answer Type an exact answer using radicals as needed

Calculus
Limits & ContinuityExplain the meaning of each of the following a lim f x 1 9 O The values of f x can be made arbitrarily large by taking a sufficiently close to but not equal to 9 O The values of f x can be made arbitrarily close to 0 by taking a sufficiently close to but not equal to 9 Of 9 O The values of f x can be made arbitrarily close to 9 by taking a sufficiently large b lim f x 2 2 Of 2 O The values of f x can be made arbitrarily close to co by taking a sufficiently close to 2 O As a approaches 2 f z approaches O The values of f x can be made negative with arbitrarily large absolute values by taking sufficiently close to but greater than 2
Calculus
Vector CalculusDetermine whether the statement is true or false If the line 7 is a vertical asymptote of y f x then f x is not defined at 7 O False O True

Calculus
Application of derivatives4 2 0 a b c e 2 lim f x 2 2 d f 2 lim f x 2 2 lim f x 2 2 4 lim f x x 4 f f 4 AX

Calculus
Limits & ContinuityExplains what it means to say that lim f x 4 and lim f x 8 2 5 2 5 O As a approaches 5 from the left f x approaches 4 As a approaches 5 from the right f x approaches 8 O As a approaches 5 f x approaches 8 but f 5 4 O As a approaches 5 f x approaches 4 but f 5 8 O As a approaches 5 from the right f x approaches 4 As a approaches 5 from the left f x approaches 8 In this situation is it possible that lim f x exists Explain z 5 OYes f x could have a hole at 5 8 and be defined such that f 5 4 O Yes f x could have a hole at 5 4 and be defined such that f 5 8 OYes if f x has a vertical asymptote at x 5 it can be defined such that lim f x 4 2 5 lim f x 8 and lim f x exists z 5 2 5 No lim f z cannot exist if lim f x lim f x 2 5 x 5
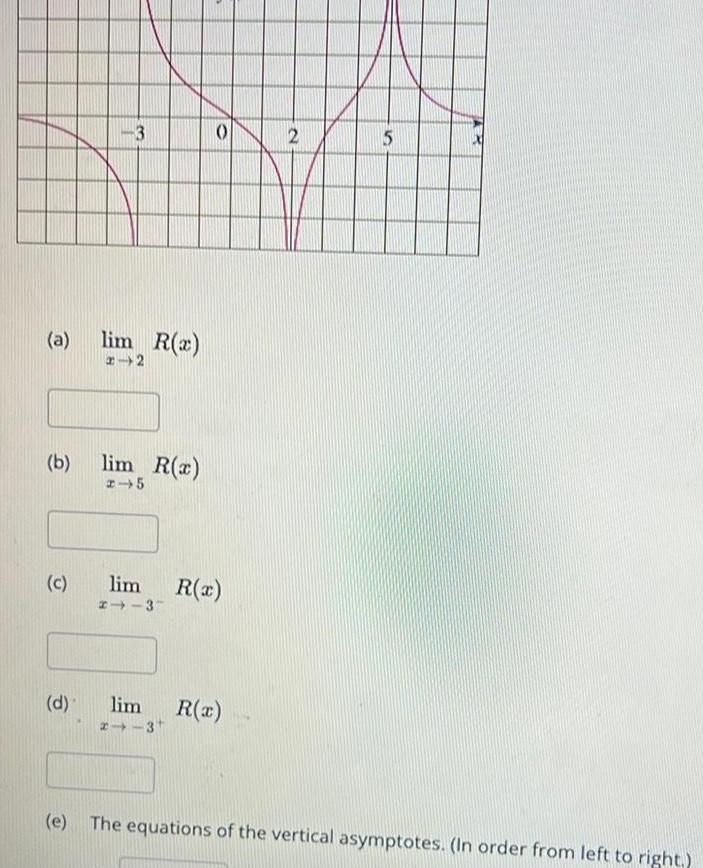
Calculus
Application of derivativesa b c d 3 lim R x 12 lim R x 215 lim 113 R x lim R x 2 3 2 5 AR e The equations of the vertical asymptotes In order from left to right
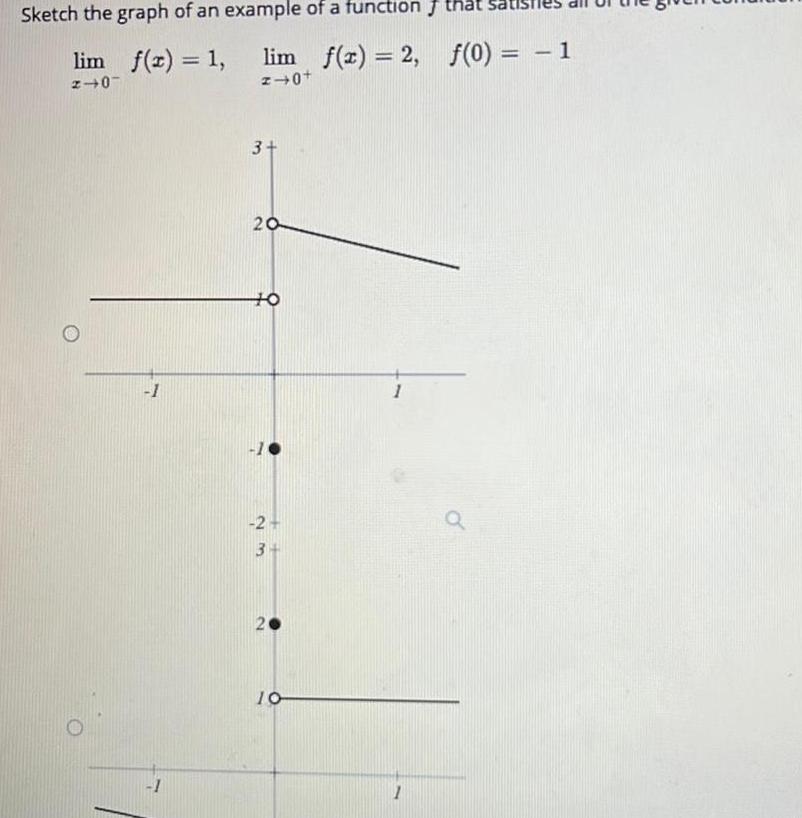
Calculus
Limits & ContinuitySketch the graph of an example of a function lim f x 1 lim f x 2 2 0 z 0 3 20 TO 2 3 10 1 f 0 1


Calculus
DifferentiationMultiply and simplify by factoring 27 24 The answer is Type Ints 0 an exact answer

Calculus
Application of derivativesMultiply and simplify by factoring Assume that all expressions under radicals represent nonnegative numbers 3 13 3 vy 3 14 13 3 16y 14 Simplify your answer Type in radical form vy 16y

Calculus
DifferentiationMultiply and then simplify by factoring if possible 2 10 2 10 Type an exact answer using radicals as needed

Calculus
Definite IntegralsFor each of the following determine if the series converges Be sure that you can rigorously demonstrate your answer A 4n 7n 1 n 1 This sum A converges O B diverges B 3 7 15 n 1 This sum O A converges OB diverges c n 7 72 0 This sum OA converges OB diverges D n n8n 16 n 7 This sum A converges B diverges
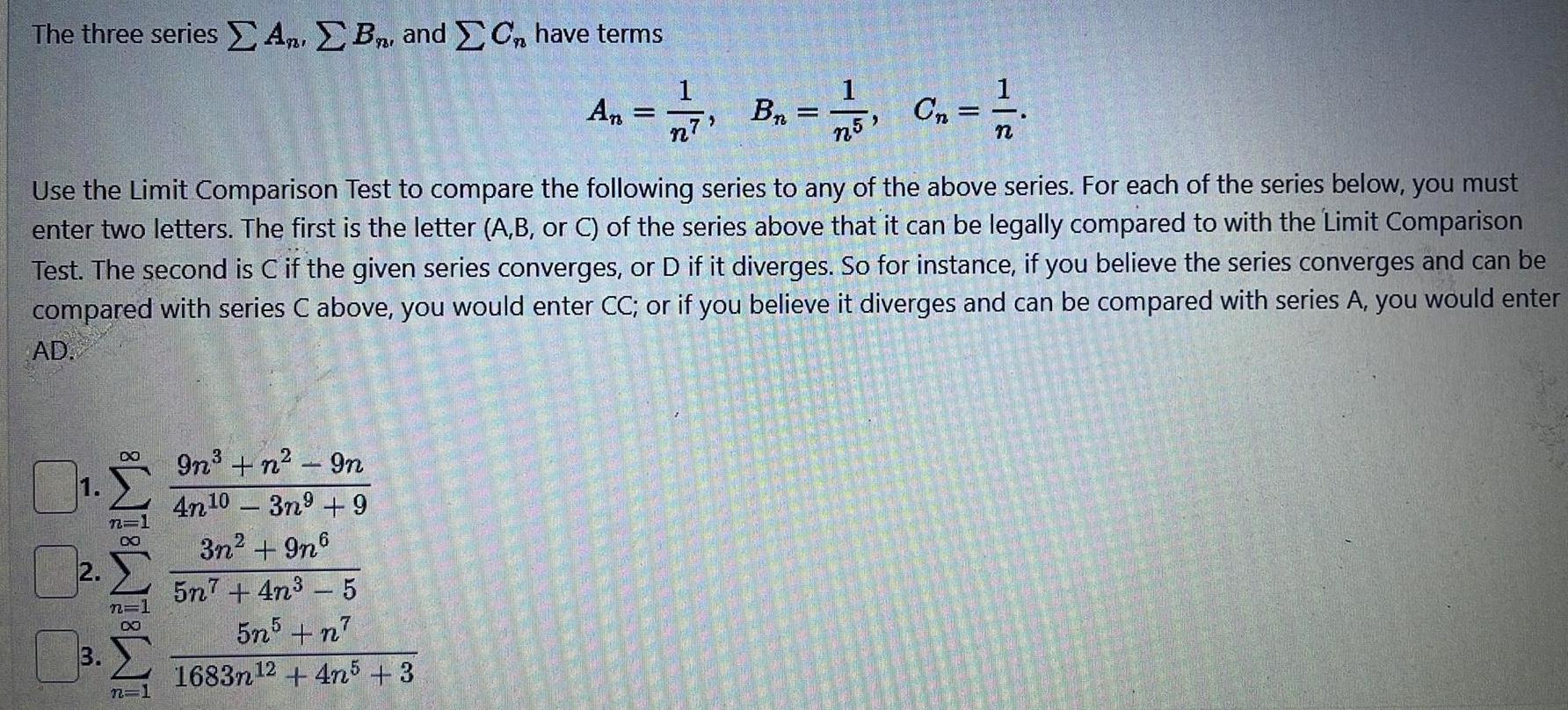
Calculus
Application of derivativesThe three series A B and C have terms Use the Limit Comparison Test to compare the following series to any of the above series For each of the series below you must enter two letters The first is the letter A B or C of the series above that it can be legally compared to with the Limit Comparison Test The second is C if the given series converges or D if it diverges So for instance if you believe the series converges and can be compared with series C above you would enter CC or if you believe it diverges and can be compared with series A you would enter AD 2 3 888 n 1 9n n 9n 4n10 3n9 9 3n 9n6 An 7 Br Cn zz n5 n 5n7 4n 5 5n5 n 1683n12 4n5 3

Calculus
Application of derivativesSimplify by factoring Assume that all expressions under the radical represent nonnegative numbers 405x y 46 46 405x y Type an exact answer using radicals as needed

Calculus
DifferentiationSimplify by factoring Assume that no radicands were formed by raising negative numbers to even powers 3 270 270 Type an exact answer using radicals as needed


Calculus
Limits & ContinuityEach of the following statements is an attempt to show that a given series is convergent or divergent using the Comparison Test NOT the Limit Comparison Test For each statement enter C for correct if the argument is valid or enter I for incorrect if any part of the argument is flawed Note if the conclusion is true but the argument that led to it was wrong you must enter I 1 For all n 2 converges 2 For all n 2 3 For all n 1 converges 4 For all n 2 5 For all n 1 arctan n n 6 For all n 2 converges 4 and the series converges so by the Comparison Test the series n In n n n 4 n n 1 converges n arctan n n n n 5 222 1 1 n 1 n 2 n2 and the series I and the series and the series 2n I n and the series and the series 2 n n T 2 converges so by the Comparison Test the series converges so by the Comparison Test the series diverges so by the Comparison Test the series 1 222 In n n n n 4 n n 1 n converges so by the Comparison Test the series converges converges so by the Comparison Test the series diverges n n2 5

Calculus
Application of derivativesTest each of the following series for convergence by either the Comparison Test or the Limit Comparison Test If at least one test can be applied to the series enter CONV if it converges or DIV if it diverges If neither test can be applied to the series enter NA Note this means that even if you know a given series converges by some other test but the comparison tests cannot be applied to it ther you must enter NA rather than CONV 3 4 5 DO n 1 n 1 DO n 1 WW 22 DO n 1 8n5 n6 3 cos n n 8n 3 8n5 n 3 5n8n6 8 n 9n 10 n5 5 cos n n n5
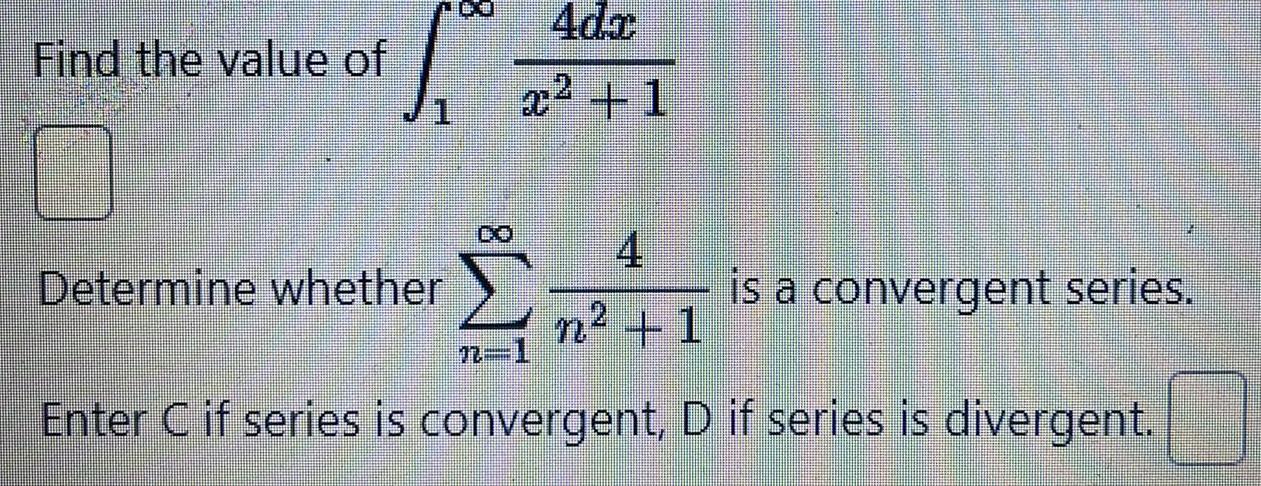
Calculus
DifferentiationFind the value of S Determine whether N 4dc x 1 4 n 1 Enter C if series is convergent D is a convergent series if series is divergent

Calculus
Definite IntegralsFind the value of 8 1 9n 2 7 n 2 Enter if series is convergent D if series is divergent Determine whether rx L 2 is a convergent series dx 9x 2 7
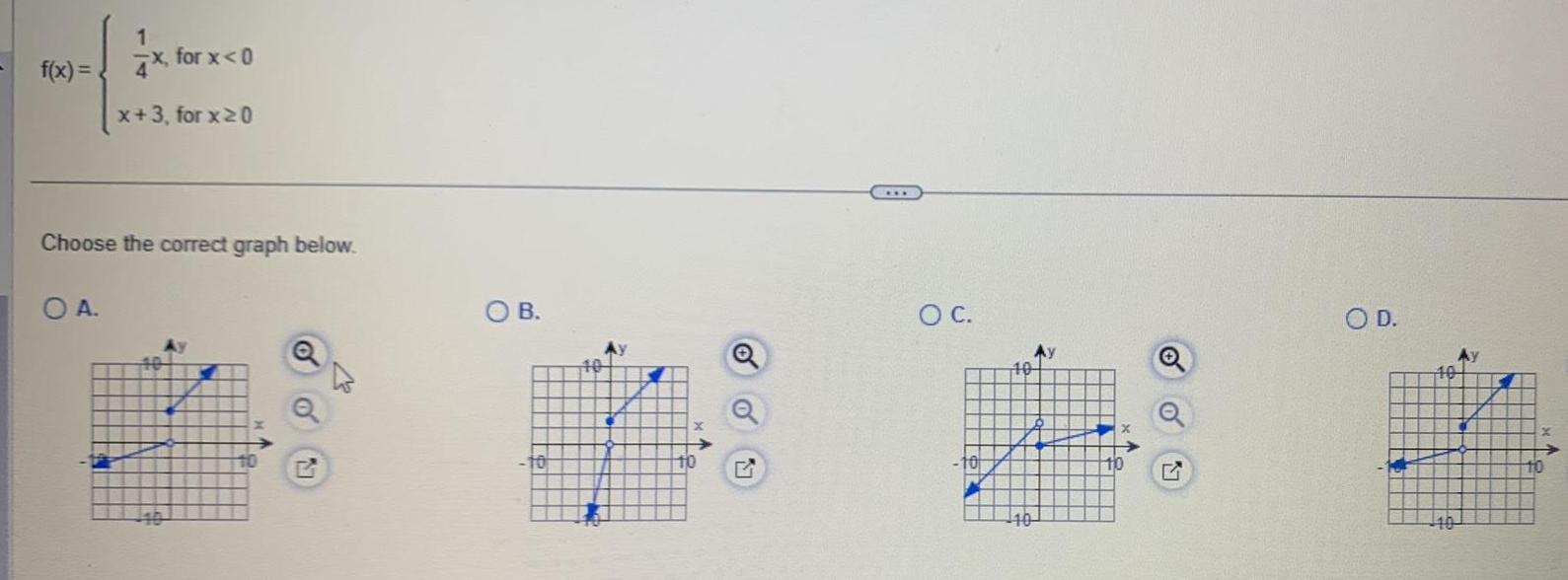
Calculus
Application of derivativesf x 1 4x for x 0 x 3 for x 0 Choose the correct graph below OA 0 Ay 10 O B O C 10 10 110 Q O D 10 10 2

Calculus
Application of derivativesWhich of the following expresses the area of the garden as a function of the length OA A x 28x x OB A x 28x x OC A x 14x x 2 OD Axl ter 2

Calculus
Application of derivativesFor the piecewise function find the values g 1 g 1 and g 2 g x x 9 for x 1 3 x for x 1 9 1 0
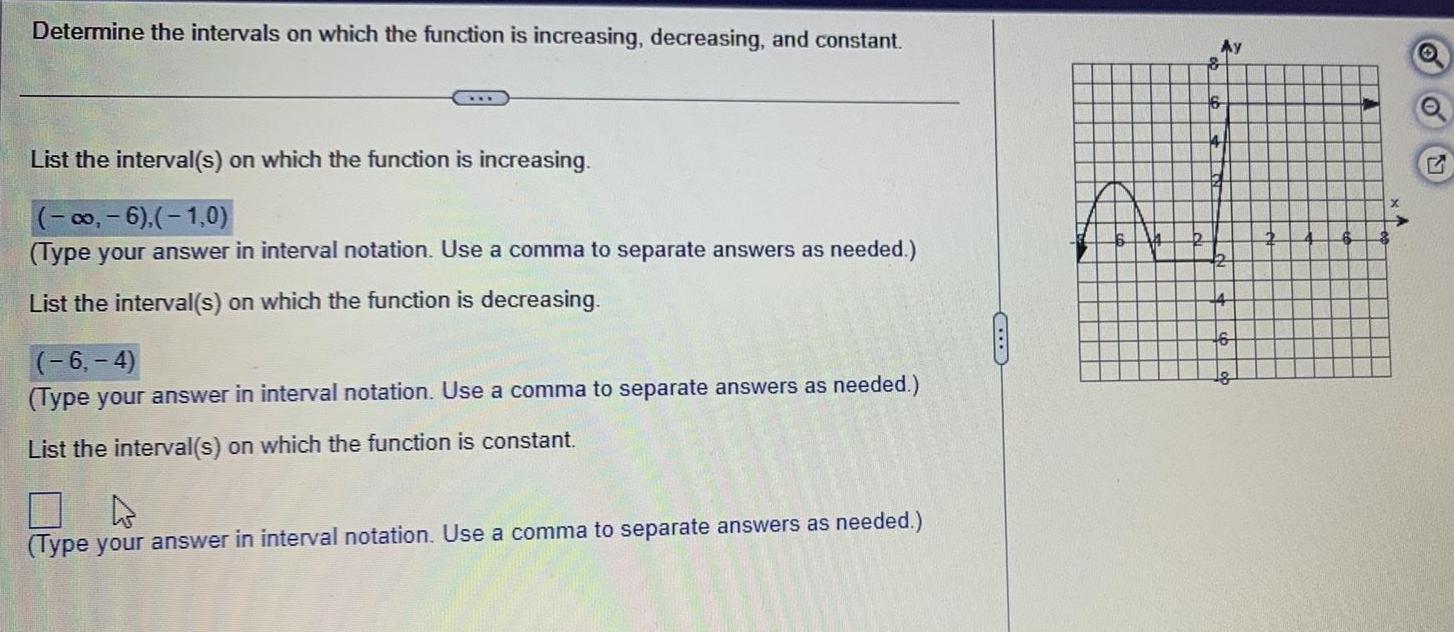
Calculus
Application of derivativesDetermine the intervals on which the function is increasing decreasing and constant List the interval s on which the function is increasing 6 1 0 Type your answer in interval notation Use a comma to separate answers as needed List the interval s on which the function is decreasing 6 4 Type your answer in interval notation Use a comma to separate answers as needed List the interval s on which the function is constant Type your answer in interval notation Use a comma to separate answers as needed Ay 16 G
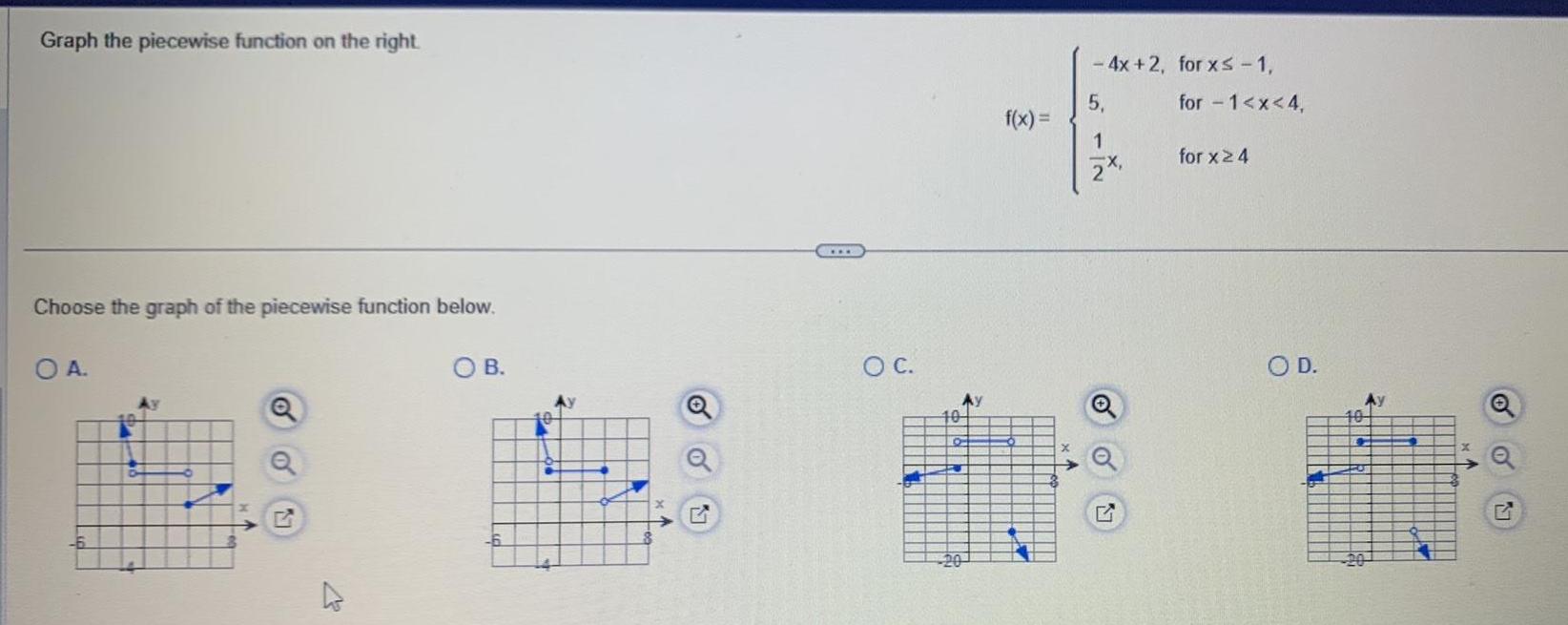
Calculus
Application of derivativesGraph the piecewise function on the right Choose the graph of the piecewise function below O A OB o 17 O C 10 Ay f x 4x 2 for x 1 5 1 for 1 x 4 for x 4 O D 104 Q
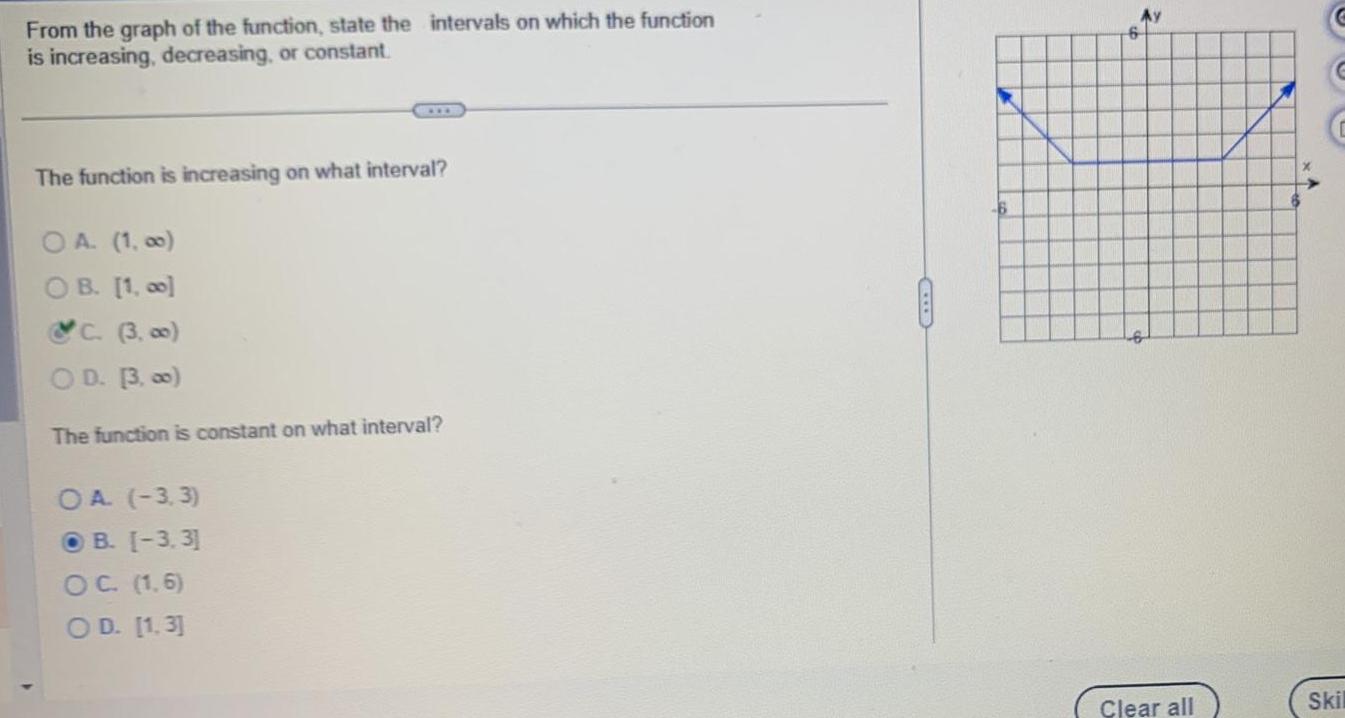
Calculus
DifferentiationFrom the graph of the function state the intervals on which the function is increasing decreasing or constant The function is increasing on what interval OA 1 00 OB 1 00 C 3 00 OD 3 00 The function is constant on what interval OA 3 3 OB 3 3 OC 1 6 OD 1 3 Clear all x Skil
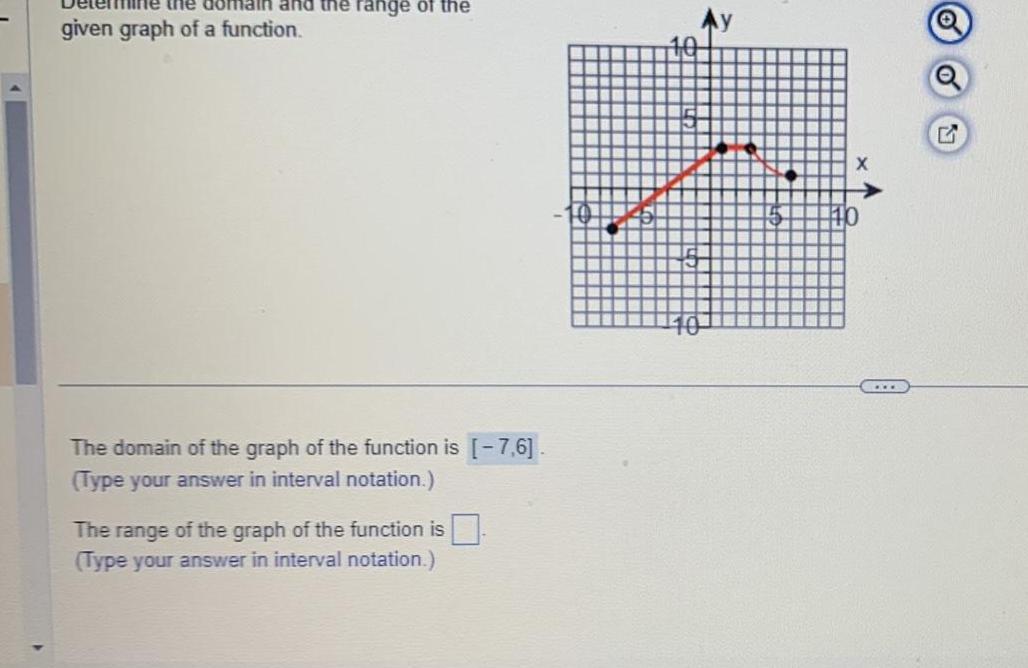
Calculus
Limits & Continuitythe domain and the range of the given graph of a function The domain of the graph of the function is 7 6 Type your answer in interval notation The range of the graph of the function is Type your answer in interval notation COLS
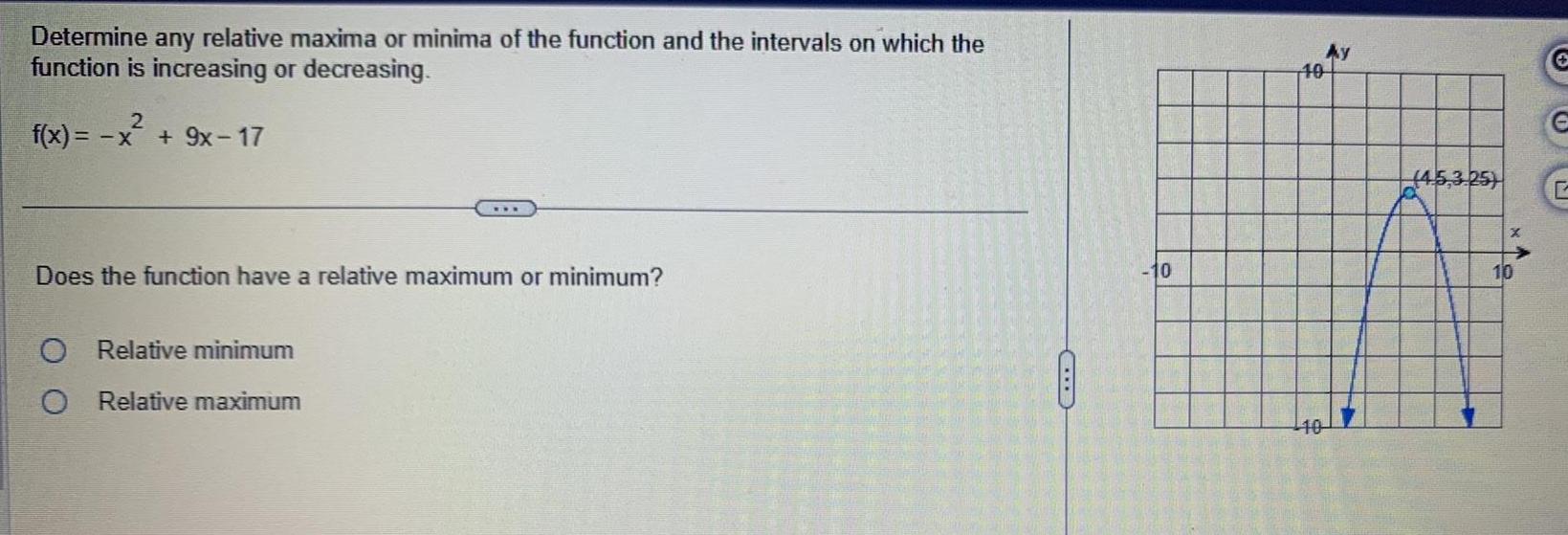
Calculus
DifferentiationDetermine any relative maxima or minima of the function and the intervals on which the function is increasing or decreasing 2 f x x 9x 17 Does the function have a relative maximum or minimum O Relative minimum O Relative maximum 10 10 10 Ay 4 5 3 25 10 C 6 C
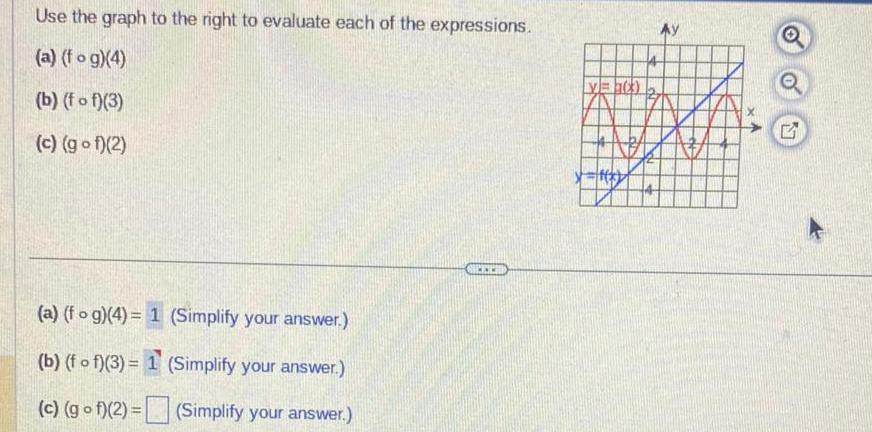
Calculus
Limits & ContinuityUse the graph to the right to evaluate each of the expressions a fog 4 b fof 3 c gof 2 a fog 4 1 Simplify your answer b fof 3 1 Simplify your answer c gof 2 Simplify your answer 0 y x 47 ST Ay

Calculus
Differential equationsDetermine whether the given function is a solution to the given differential equation d 0 de dt 8 4t 5t 0 40 12e5t dt
Calculus
Application of derivativesClick the Secant Line Slope of Secant and Values boxes Set the x slider to the point x 4 5 and the x h slider 5 Complete parts 1 through 3 below Use the interactive figure to find your answer Use the left and right arrow keys to move along a slider as needed Click here to launch the interactive figure BECKH Part 1 What is the slope m of the secant line when x 4 5 and h 0 5
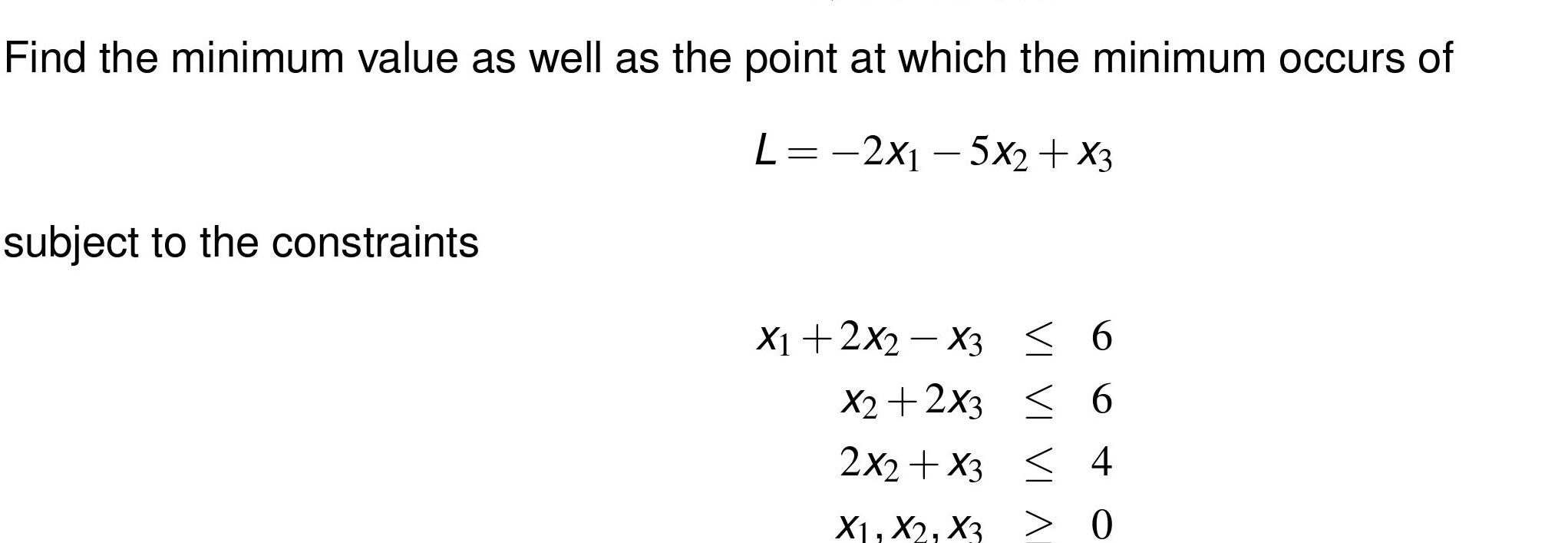
Calculus
Differential equationsFind the minimum value as well as the point at which the minimum occurs of L 2x 5x2 x3 subject to the constraints VI X1 2X2 X3 6 X2 2X3 6 2x2 x3 4 X1 X2 X3 0

Calculus
DifferentiationFor each of the following series indicate whether the integral test can be used to determine its convergence or not and if not why cos n A M Can the integral test be used to test convergence O A no because the terms in the series do not decrease in magnitude B no because the terms in the series are not all positive for n c for some c 0 C no because the series is not a geometric series D no because the terms in the series are not recursively defined O E no because the terms in the series are not defined for all n O F yes B n 7 Can the integral test be used to test convergence A no because the terms in the series do not decrease in magnitude B no because the terms in the series are not all positive for n c for some c 0 C no because the series is not a geometric series D no because the terms in the series are not recursively defined E no because the terms in the series are not defined for all n F yes

Calculus
Differential equationsUse the integral test to determine whether each of the following series converges or diverges For each fill in the integrand and the value of the integral Enter diverges if the integral diverges Then indicate the convergence of the sum A ZT n 1 Compare with f dx Evaluate your integral with bottom limit c 1 This sum O A converges O B diverges 8 B n 7 n 14n 2 8 Compare with fdx Evaluate your integral with bottom limit c 1 This sum O A converges B diverges
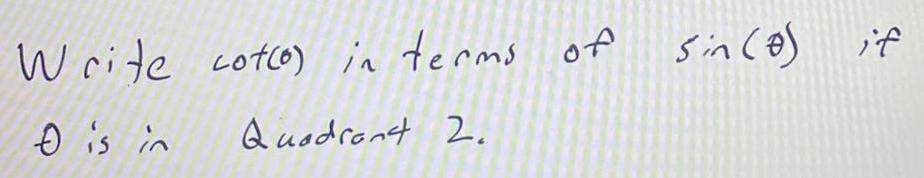
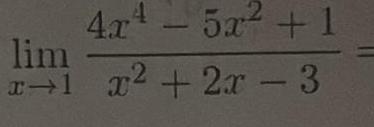


Calculus
Application of derivativesquestion Taking logarithms and antilogarithms is necessary to solve many chemistry problems For practice complete the following table where N is a number N log N 8 86 In N 4 449
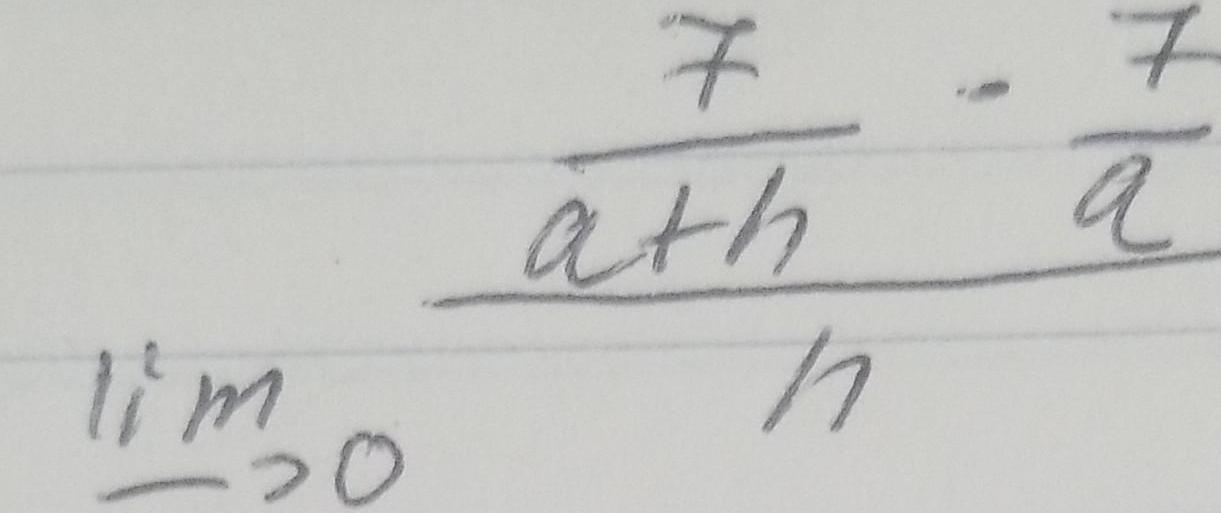

Calculus
Definite IntegralsLet R be the region bounded by the curves y 1 x 2 y 0 x 1 and x 5 What is the volume of the solid generated by rotating R about the x axis

Calculus
Vector CalculusIn March 2014 a gas company had the rate schedule shown to the right for natural gas usage in single family residences a What is the charge for using 30 therms in a month b What is the charge for using 200 therms in a month c Develop a function that models the monthly charge C for x therms of gas d Graph the function found in part c a The charge for using 30 therms in a month is b The charge for using 200 therms in a month is c C x if 0 x if x Simplify your answers Monthly service charge Delivery charge First 40 therms Over 40 therms Natural gas cost First 40 therms Over 40 therms Simplify your answer Round to the nearest cent Simplify your answer Round to the nearest cent 18 5 0 70202 therm 0 0 3049 therm 0 5637 therm

Calculus
Application of derivatives1 point The table below A f d the amount of money A in billions of dollars in bills of denomination d circulating in US currency in 2005 For example according to the table values below there wer 60 2 billion worth of 50 bills in circulation a Find f 50 60 2 b Using your answer in a what was the total number of 50 bills not amount of money in circulation in 2005 There was a total number of 50 billion 50 bills in circulation c Are the following statements True or False False False V 1 There were more 1 dollar bills than 5 dollar bills Denomination value of bill 1 5 10 20 50 100 Dollar Value in Circulation 8 49 7 14 8 110 160 2 524 5 2 There were more 5 dollar bills than 10 dollar bills
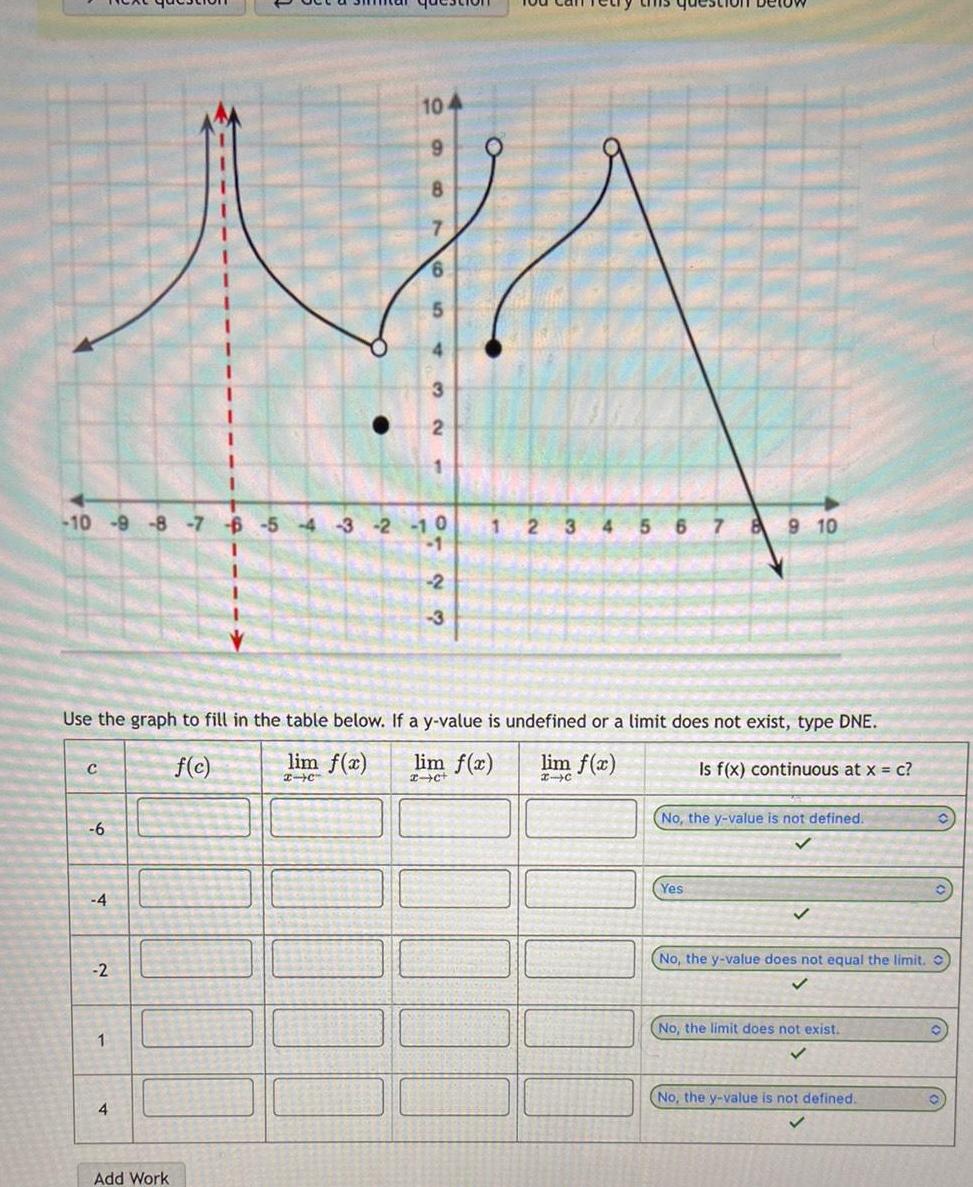
Calculus
Limits & Continuity10 9 8 NA 6 10 9 8 7 6 5 4 3 2 10 1 2 1 C 6 4 2 Use the graph to fill in the table below If a y value is undefined or a limit does not exist type DNE lim f x lim f x f c lim I C 2 c 1 32 4 Add Work 3 3 4 5 6 7 8 9 10 Yes Is f x continuous at x c No the y value is not defined No the y value does not equal the limit No the limit does not exist No the y value is not defined O
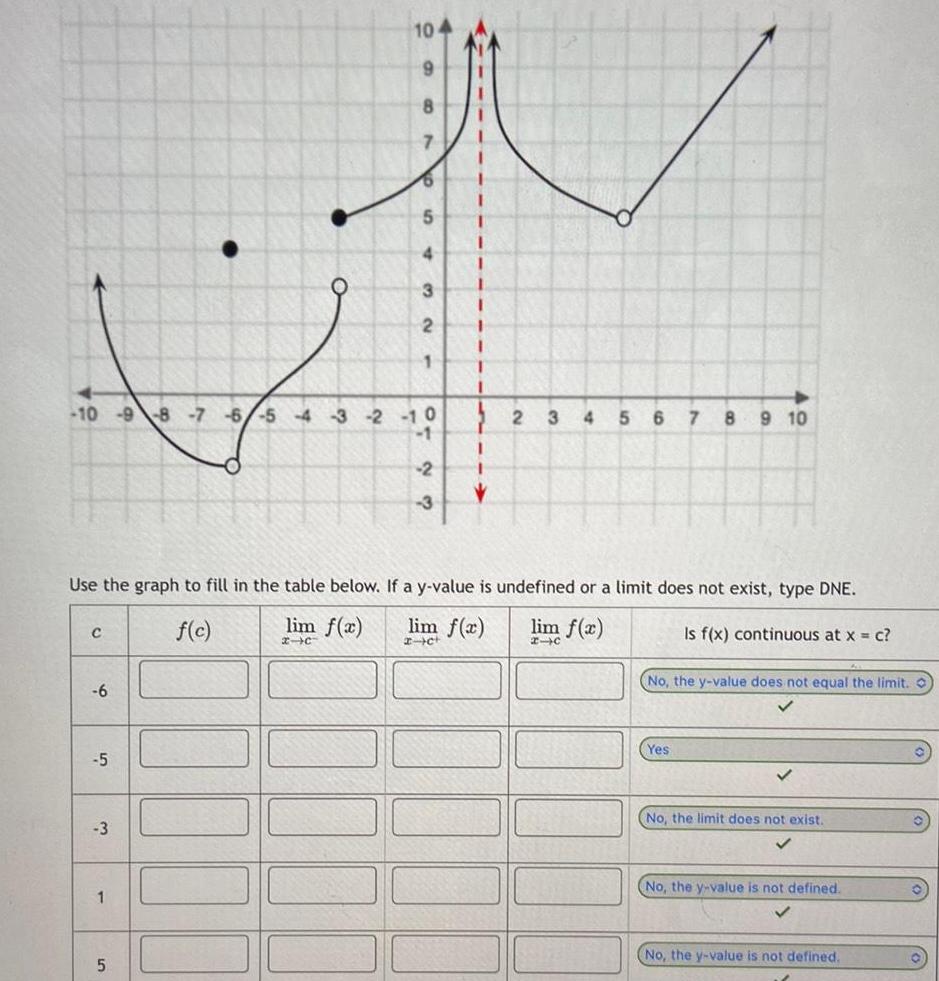
Calculus
Limits & Continuity10 9 8 7 6 5 4 3 2 C 6 5 3 1 5 5 4 3 2 1 0 Use the graph to fill in the table below If a y value is undefined or a limit does not exist type DNE f c lim f x lim f x lim f x x c x c 2 3 1 2 3 4 5 6 7 8 9 10 Is f x continuous at x c No the y value does not equal the limit O Yes No the limit does not exist No the y value is not defined No the y value is not defined O 0

Calculus
Limits & ContinuityThe limit 2 h 4 h is the standard expression defining the derivative of some function f x at some number a Find f and a f x a lim h 0
Calculus
Application of derivativesSimilar question You can retry this question below A bungee jumper dives from a tower at time t 0 Her heights in feet at time t in seconds is given by 0 2t s t 300 cos 0 75t e 300 a Write an expression for the average velocity of the bungee jumper on the interval 1 1 h AV 1 1 h Use computing technology to estimate the value of the limit as h 0 of the quantity you found in a lim AV 1 1 h h 0 feet per second What is the meaning of the value of the limit in b What are the units The instantaneous velocity of the bungee jumper at the moment t 1 is approximately
Calculus
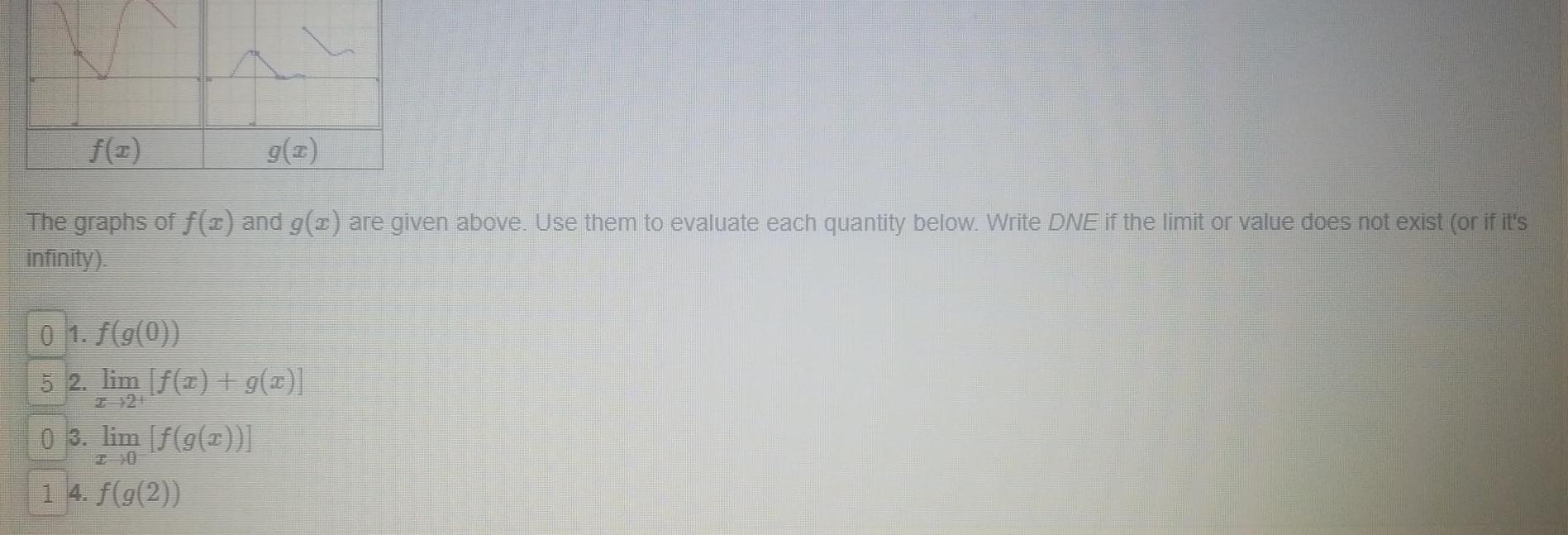
Limits & Continuityf x The graphs of f x and g x are given above Use them to evaluate each quantity below Write DNE if the limit or value does not exist or if it s infinity 01 f g 0 5 2 lim 1 g x 2 21 03 lim f g x 1 4 f g 2
Calculus
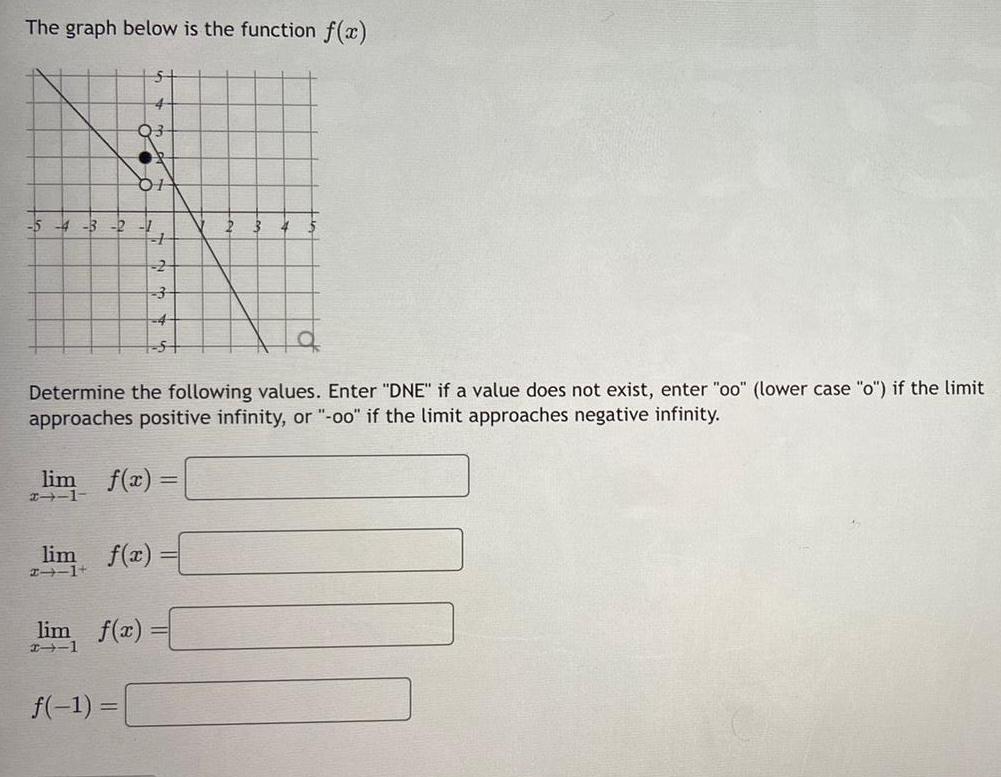
Limits & ContinuityThe graph below is the function f x 03 5 4 3 2 1 01 5 f 1 H lim f x 21 1 2 4 lim f x 111 lim f x Determine the following values Enter DNE if a value does not exist enter oo lower case o if the limit approaches positive infinity or oo if the limit approaches negative infinity 2 3 4